La réciproque d’une fonction racine carrée est une fonction polynomiale de degré 2 dont le domaine est réduit.
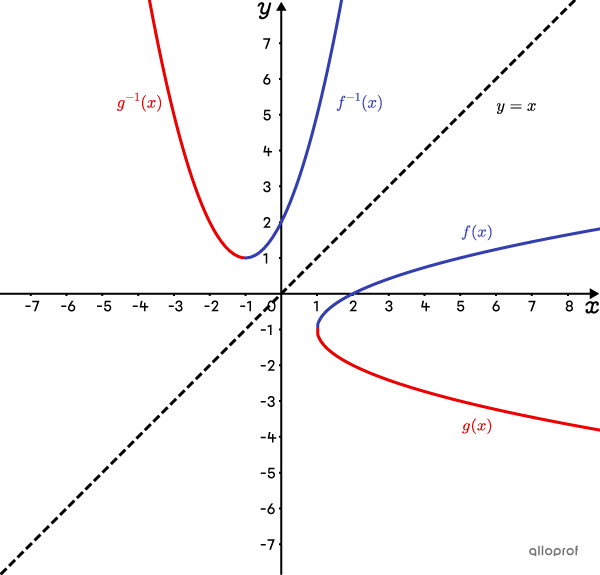
Dans ce graphique, |\color{#333fb1}{f^{-1}(x)}| est la réciproque de la fonction racine carrée |\color{#333fb1}{f(x)}.| On remarque que le domaine de |\color{#333fb1}{f^{-1}(x)}| est équivalent à l’image de |\color{#333fb1}{f(x)}.| Il en va de même pour |\color{#ec0000}{g^{-1}(x)}| et |\color{#ec0000}{g(x)}.|
Ainsi, il suffit de calculer l’image de la fonction initiale pour trouver la restriction sur le domaine de la fonction réciproque.
Voici comment procéder pour trouver la règle de la réciproque lorsqu’on connait celle de la fonction.
-
Interchanger |\color{#ec0000}{x}| et |\color{#333fb1}{y}| dans la règle de la fonction.
-
Isoler |\color{#333fb1}{y}.|
-
Calculer la restriction sur le domaine de la réciproque à partir de l’image de la fonction. Pour |f(x)=a\sqrt{b(x-h)}+k:|
|\text{dom}\ f^{-1}=\text{ima}\ f=\ ]-\infty,k]| si |a<0|
ou
|\text{dom}\ f^{-1}=\text{ima}\ f=\ [k,+\infty[| si |a>0.| -
Donner la règle de la réciproque.
Trouve la règle de la réciproque de la fonction |f(x)=2\sqrt{x-5}+10.|
-
Interchanger |x| et |y| dans la règle
||\begin{align}\color{#333fb1}{y}&=2\sqrt{\color{#ec0000}{x}-5}+10\\ \color{#ec0000}{x}&=2\sqrt{\color{#333fb1}{y}-5}+10\end{align}||
-
Isoler |y|
||\begin{align}x&=2\sqrt{y-5}+10\\ x-10&=2\sqrt{y-5}\\ \dfrac{x-10}{2}&=\sqrt{y-5}\\ \color{#ec0000}{\left(\color{black}{\dfrac{x-10}{2}}\right)^2}&=\color{#ec0000}{\left(\color{black}{\sqrt{y-5}}\ \right)^2}\\ \dfrac{(x-10)^2}{4}&=y-5\\ \dfrac{1}{4}(x-10)^2+5&=y\end{align}||
-
Calculer la restriction sur le domaine de la réciproque
Pour |f(x),| |a=2| et |k=10.|
Le paramètre |a| de |f(x)| est positif, ce qui implique que la fonction est définie en haut de son sommet. Ainsi, le domaine de la fonction réciproque |f^{-1}(x),| qui est équivalent à l’image de |f(x),| est le suivant.||\begin{align}\text{dom}\ f^{-1}=\text{ima}\ f&=[k,+\infty[\\&=[10,+\infty[\end{align}||
-
Donner la règle
La réciproque de la fonction |f(x)| est |f^{-1}(x)=\dfrac{1}{4}(x-10)^2+5| où |x\ge10.|
Dans le plan cartésien ci-dessous, on retrouve les courbes de |\color{#333fb1}{f(x)}| et de |\color{#ec0000}{f^{-1}(x)}| de l’exemple précédent.
Il est possible de tracer la réciproque d’une fonction en interchangeant les coordonnées |x| et |y| de certains points. Par exemple, le sommet |(\color{#333fb1}{5},\color{#333fb1}{10})| devient le sommet |(\color{#ec0000}{10},\color{#ec0000}{5})| et le point |(\color{#333fb1}{9},\color{#333fb1}{14})| devient |(\color{#ec0000}{14},\color{#ec0000}{9}).|

On peut aussi dire que |\color{#ec0000}{f^{-1}(x)}| correspond à la réflexion de |\color{#333fb1}{f(x)}| par rapport à l’axe d’équation |y=x.| Il est donc possible de tracer la réciproque par réflexion. Par contre, la graduation des axes |x| et |y| doit être dans un rapport |1:1.|