Afin de résoudre un problème faisant appel à la fonction tangente, il est souvent utile de faire une représentation graphique de la situation. En général, on doit déterminer la règle de la fonction tangente pour être en mesure de répondre aux questions. De plus, il arrive souvent qu’on doive résoudre une équation tangente.
Il est important de mettre sa calculatrice en radian (RAD) lorsqu’on travaille avec les fonctions trigonométriques.
Voici les étapes principales à suivre pour résoudre un problème à l’aide de la fonction tangente.
-
Identifier les variables.
-
Placer les informations dans un plan cartésien et faire un croquis de la courbe.
-
Déterminer la règle de la fonction.
-
Répondre aux questions.
Puisque la fonction tangente est périodique, il existe plusieurs valeurs de |x| possibles pour un |y| donné.
Voici une vidéo présentant un exemple de résolution de problèmes impliquant la fonction tangente.
Enya participe à une compétition de drones lors de laquelle elle doit effectuer certaines manœuvres. L’une d’entre elles suit une trajectoire correspondant à une fonction tangente. On s’intéresse à la hauteur du drone en fonction de la distance horizontale entre le drone et la concurrente.
Voici les caractéristiques de cette trajectoire.
-
À |11| mètres de haut, le drone doit être à une distance de |9{,}38| mètres à l’horizontale.
-
À |15| mètres de haut, le drone doit être à une distance d’environ |10{,}65| mètres à l’horizontale.
-
Enya doit être située à l’origine du plan cartésien.
-
À |11| mètres de la concurrente se trouve un édifice que le drone doit longer.
a) Lorsque le drone est à une distance de |2| mètres à l’horizontale, à quelle hauteur se situe-t-il?
b) Lorsque le drone est à |12| mètres de haut, quelle distance horizontale a-t-il parcouru?
c) Si le drone d’Enya est à une distance de |1| mètre à l’horizontale et à |8| mètres de haut, est-ce que la trajectoire a été respectée?
-
Identifier les variables
|x :| distance horizontale (m)
|y :| hauteur (m) -
Placer les informations dans un plan cartésien et faire un croquis de la courbe
Les 2 premières caractéristiques du problème nous permettent de déduire 2 points : |(9{,}38;11)| et |(10{,}65;15).|
Comme Enya se tient à l’origine du plan cartésien, on en déduit une 1re asymptote : |x=0.|
L’édifice situé |11| mètres plus loin représente la 2e asymptote : |x=11.|
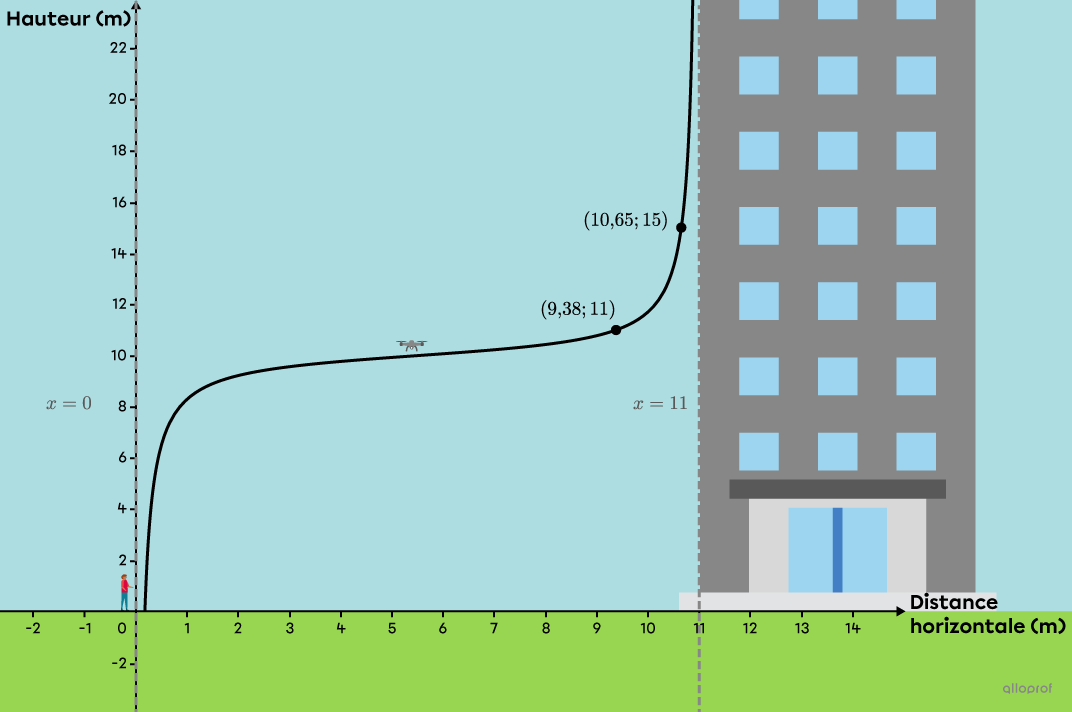
-
Déterminer la règle de la fonction
Déterminer la règle de la fonction permet de répondre précisément aux questions. La règle sous forme canonique d’une fonction tangente est |f(x)=a\tan\!\big(b(x-h)\big)+k.| Avec les informations fournies, on se retrouve avec 2 points quelconques et des asymptotes consécutives connus.
Déterminer la période avec les 2 asymptotes
La différence entre les abscisses des asymptotes donne la valeur de la période.||p=11-0=11||
Déterminer la valeur de |b|
On détermine la valeur de |\vert b\vert| grâce à la période.||\begin{align}\vert b\vert&=\dfrac{\pi}{p}\\&=\dfrac{\pi}{11}\end{align}||Pour déterminer le signe de |b,| on analyse la croissance de la fonction. À l’aide du croquis, on voit que la fonction est croissante. Ainsi, |a| et |b| sont de même signe. On prend une valeur positive pour les 2 paramètres.||b=\dfrac{\pi}{11}||
Déterminer la valeur de |h|
La valeur du paramètre |h| se détermine en faisant la moyenne des abscisses des asymptotes.||h=\dfrac{11+0}{2}=5{,}5||
Bâtir un système d’équations et le résoudre
On forme 2 équations à 2 inconnues à l’aide des couples qui sont fournis.
En utilisant le couple |(9{,}38;11),| on obtient la 1re équation.||11=\color{#3b87cd}a\tan\!\left(\dfrac{\pi}{11}(9{,}38-5{,}5)\right)+\color{#3A9A38}k||On isole |k.|||\begin{align}11&=\color{#3b87cd}a\tan\!\left(\dfrac{\pi}{11}(3{,}88)\right)+\color{#3A9A38}k\\11&\approx\color{#3b87cd}a\tan(1{,}108\,1)+\color{#3A9A38}k\\11&\approx2\color{#3b87cd}a+\color{#3A9A38}k\\11-2\color{#3b87cd}a&\approx\color{#3A9A38}k\end{align}||
En utilisant le couple |(10{,}65;15),| on obtient la 2e équation.||15=\color{#3b87cd}a\tan\!\left(\dfrac{\pi}{11}(10{,}65-5{,}5)\right)+\color{#3A9A38}k||On isole |k.|||\begin{align}15&=\color{#3b87cd}a\tan\!\left(\dfrac{\pi}{11}(5{,}15)\right)+\color{#3A9A38}k\\15&\approx\color{#3b87cd}a\tan(1{,}470\,8)+\color{#3A9A38}k\\15&\approx9{,}97\color{#3b87cd}a+\color{#3A9A38}k\\15-9{,}97\color{#3b87cd}a&\approx\color{#3A9A38}k\end{align}||
On utilise la méthode de comparaison pour déterminer la valeur de |a.|||\begin{align}11-2\color{#3b87cd}a&=15-9{,}97\color{#3b87cd}a\\7{,}97\color{#3b87cd}a&=4\\\color{#3b87cd}{a}&\approx \color{#3b87cd}{0{,}5}\end{align}||On détermine la valeur de |k| en utilisant l’une ou l’autre des 2 équations formées précédemment.||\begin{align}11-2\color{#3b87cd}a&=\color{#3A9A38}k\\11-2(\color{#3b87cd}{0{,}5})&=\color{#3A9A38}k\\10&=\color{#3A9A38}k\end{align}||La règle de la fonction est donc |f(x)=0{,}5\tan\left(\dfrac{\pi}{11}(x-5{,}5)\right)+10.|
-
Répondre aux questions
a) Lorsque le drone est à une distance de |2| mètres à l’horizontale, à quelle hauteur se situe-t-il?
Répondre à cette question revient à rechercher la valeur de |\color{#FA7921}{f(x)}| lorsque |\color{#560FA5}{x=2}.|||\begin{align}\color{#FA7921}{f(x)}&=0{,}5\tan\left(\dfrac{\pi}{11}(\color{#560FA5}x-5{,}5)\right)+10\\\color{#FA7921}{f(x)}&=0{,}5\tan\left(\dfrac{\pi}{11}(\color{#560FA5}2-5{,}5)\right)+10\\\color{#FA7921}{f(x)}&=0{,}5\tan\left(\dfrac{\pi}{11}(-3{,}5)\right)+10\\\color{#FA7921}{f(x)}&\approx0{,}5(-1{,}556)+10\\\color{#FA7921}{f(x)}&\approx9{,}22\end{align}||Réponse : Lorsque le drone est à une distance de |2| mètres à l’horizontale, il se situe à environ |9{,}22| mètres de haut.
b) Lorsque le drone est à |12| mètres de haut, quelle distance horizontale a-t-il parcouru?
Cette fois-ci, on cherche la valeur de |\color{#560FA5}x| lorsque |\color{#FA7921}{f(x)=12}.| Il faudra donc résoudre une équation tangente.||\begin{align}\color{#FA7921}{f(x)}&=0{,}5\tan\left(\dfrac{\pi}{11}(\color{#560FA5}x-5{,}5)\right)+10\\\color{#FA7921}{12}&=0{,}5\tan\left(\dfrac{\pi}{11}(\color{#560FA5}x-5{,}5)\right)+10\\2&=0{,}5\tan\left(\dfrac{\pi}{11}(\color{#560FA5}x-5{,}5)\right)\\4&=\tan\left(\dfrac{\pi}{11}(\color{#560FA5}x-5{,}5)\right)\\\color{#EC0000}{\tan^{-1}(}4\color{#EC0000})&=\dfrac{\pi}{11}(\color{#560FA5}x-5{,}5)\\1{,}3258&\approx\dfrac{\pi}{11}(\color{#560FA5}x-5{,}5)\\4{,}6422&\approx\color{#560FA5}x-5{,}5\\10{,}14&\approx\color{#560FA5}x\end{align}||Réponse : Lorsque le drone est à |12| mètres de haut, il a parcouru environ |10{,}14| mètres à l’horizontale.
c) Si le drone d’Enya est à une distance de |1| mètre à l’horizontale et à |8| mètres de haut, est-ce que la trajectoire a été respectée?
Pour répondre à cette question, il faut vérifier si le point |(1,8)| est un point qui appartient à la fonction. On peut remplacer |x| par |1| dans la règle et vérifier si le résultat est bien équivalent à |8.|||\begin{align}\color{#FA7921}{f(x)}&=0{,}5\tan\left(\dfrac{\pi}{11}(\color{#560FA5}x-5{,}5)\right)+10\\\color{#FA7921}{f(1)}&=0{,}5\tan\left(\dfrac{\pi}{11}(\color{#560FA5}1-5{,}5)\right)+10\\\color{#FA7921}{f(1)}&\approx0{,}5\tan(-1{,}285\,2)+10\\\color{#FA7921}{f(1)}&\approx8{,}297\end{align}||Réponse : Le drone d’Enya n’a pas respecté la trajectoire, puisqu’il est passé à environ |0{,}3| mètre au-dessus de la trajectoire demandée.