Une équation ou une inéquation tangente contient un rapport tangente, où l’inconnue |(x)| apparait dans l’argument.
Puisque la fonction tangente est périodique, ce type d’équation peut ne posséder aucune solution, peut posséder une solution, plusieurs solutions ou une infinité de solutions.
De plus, il est nécessaire d’utiliser les angles en radians.
Dans le cercle trigonométrique, la tangente d’un angle n’est pas directement observable, puisqu’elle correspond au rapport entre l’ordonnée et l’abscisse du point associé à cet angle sur le cercle. Pour résoudre une équation tangente, on peut utiliser les valeurs remarquables du rapport tangente ou la fonction réciproque |\boldsymbol{\arctan}.|
Lorsqu’on utilise la fonction réciproque |\arctan,| le résultat obtenu est toujours un angle situé dans le 1er quadrant ou dans le 4e quadrant du cercle trigonométrique. Autrement dit, l’angle est compris entre |-\dfrac{\pi}{2}| et |\dfrac{\pi}{2}.|
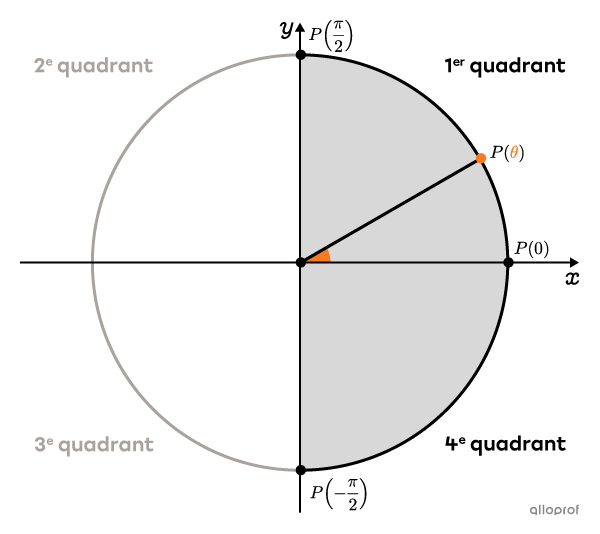
La fonction réciproque |\arctan| est parfois notée |\tan^{-1},| notamment sur les calculatrices.
Il existe quelques valeurs remarquables du rapport tangente, qu’on peut utiliser lors de la résolution d’une équation ou d’une inéquation tangente.
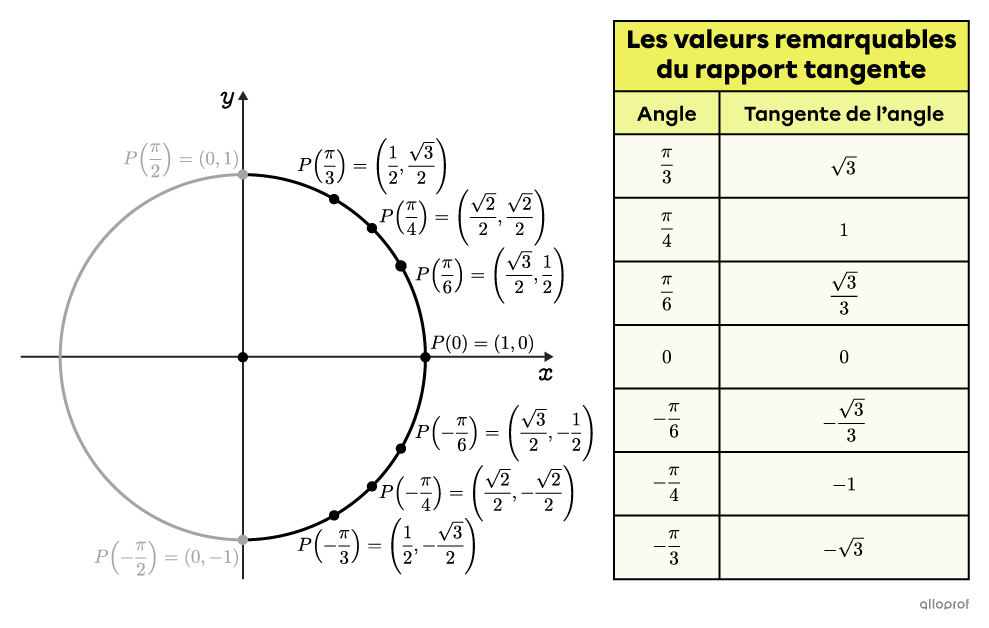
On obtient ces valeurs en faisant le rapport de l’ordonnée et de l’abscisse des points remarquables du 1er quadrant et du 4e quadrant du cercle trigonométrique. Voici un exemple de calcul avec l’angle |-\dfrac{\pi}{6}.|||\begin{align}\tan\left(-\dfrac{\pi}{6}\right)&=\dfrac{\sin\left(-\dfrac{\pi}{6}\right)}{\cos\left(-\dfrac{\pi}{6}\right)}\\[3pt]&=\dfrac{-\dfrac{1}{2}}{\dfrac{\sqrt{3}}{2}}\\[3pt]&=-\dfrac{1}{\color{#ec0000}{\cancel{\color{black}{2}}}}\times\dfrac{\color{#ec0000}{\cancel{\color{black}{2}}}}{\sqrt{3}}\\[3pt]&=-\dfrac{1}{\sqrt{3}}\boldsymbol{\color{#ec0000}{\times\dfrac{\sqrt{3}}{\sqrt{3}}}}\\[3pt]&=-\dfrac{\sqrt{3}}{3}\end{align}||Remarque : Il n’y a pas de valeur remarquable pour les angles |\dfrac{\pi}{2}| et |-\dfrac{\pi}{2},| car on obtient une division par |0.| D’ailleurs, c’est pour cette raison que la fonction |\tan(x)| de base a des asymptotes à |x=\dfrac{\pi}{2}| et |x=-\dfrac{\pi}{2}.|
La démarche à suivre pour résoudre une équation tangente est la suivante.
-
Isoler le rapport tangente.
-
Déterminer l’angle trigonométrique à l’aide du tableau des valeurs remarquables ou de la fonction réciproque |\boldsymbol{\arctan}.|
-
Résoudre l’équation obtenue avec l’angle trigonométrique.
-
Calculer la période de la fonction tangente.
-
Donner les solutions de l’équation.
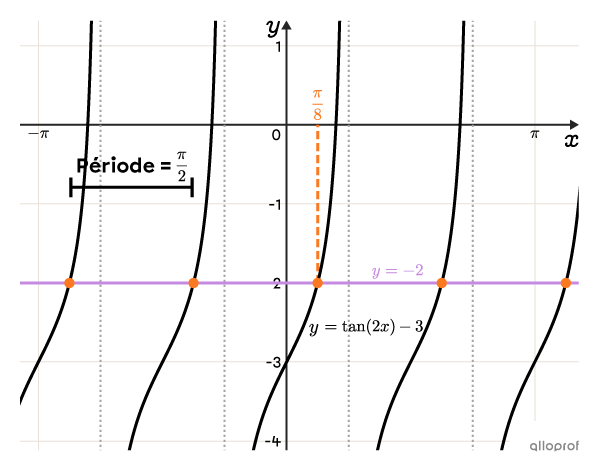
Voici un exemple où on utilise le tableau des valeurs remarquables du rapport tangente pour résoudre l’équation.
Résous l’équation suivante.||\tan(2x)-3=-2||
Résous l’équation suivante.||\tan(2x)-3=-2||
-
Isoler le rapport tangente
||\begin{align}\tan(2x)-3&=-2\\\tan(2x)&=1\end{align}|| -
Déterminer l’angle trigonométrique
|
Angle |
Tangente de l’angle |
|---|---|
|
||\dfrac{\pi}{3}|| |
||\sqrt{3}|| |
|
||\boldsymbol{\color{#fa7921}{\dfrac{\pi}{4}}}|| |
||\boldsymbol{\color{#c58ae1}{1}}|| |
|
||\dfrac{\pi}{6}|| |
||\dfrac{\sqrt{3}}{3}|| |
|
||0|| |
||0|| |
|
||-\dfrac{\pi}{6}|| |
||-\dfrac{\sqrt{3}}{3}|| |
|
||-\dfrac{\pi}{4}|| |
||-1|| |
|
||-\dfrac{\pi}{3}|| |
||-\sqrt{3}|| |
Puisque |\boldsymbol{\color{#c58ae1}{1}}| est une valeur remarquable du rapport tangente, on détermine l’angle recherché directement à partir du tableau des valeurs remarquables.
On trouve que l’angle pour lequel le rapport tangente vaut |1| est |\boldsymbol{\color{#fa7921}{\dfrac{\pi}{4}}}.|
-
Résoudre l’équation
||\begin{align}\tan(2x)&=1\\ &\Downarrow\\2x&=\dfrac{\pi}{4}\\[3pt]\boldsymbol{\color{#fa7921}{x_1}}&=\boldsymbol{\color{#fa7921}{\dfrac{\pi}{8}}}\end{align}|| -
Calculer la période de la fonction tangente
Comme la fonction tangente est périodique, il faut calculer la période pour être en mesure de donner toutes les solutions.||\begin{align}p&=\dfrac{\pi}{\vert b\vert}\\[3pt]&=\dfrac{\pi}{\vert2\vert}\\[3pt]&=\dfrac{\pi}{2}\end{align}||
-
Donner les solutions de l’équation
Les solutions de l’équation |\tan(2x)-3=-2| sont donc les suivantes.
||x=\dfrac{\pi}{8}+\dfrac{\pi}{2}n||où||n\in\mathbb{Z}||
Voici un exemple où on utilise la fonction réciproque arc tangente pour résoudre l’équation.
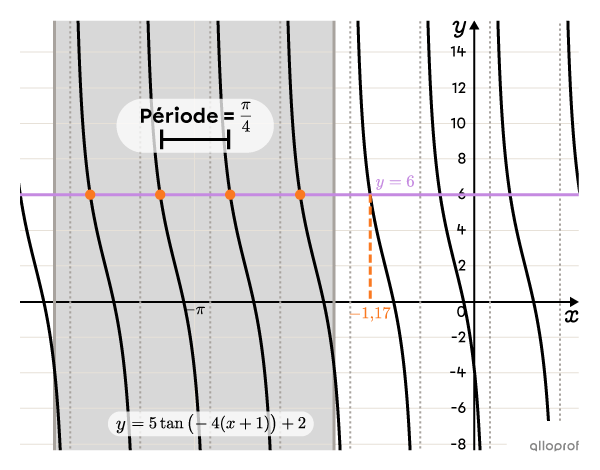
Résous l’équation suivante dans l’intervalle |\left[-\dfrac{3\pi}{2},-\dfrac{\pi}{2}\right].|||5\tan\big(\!-4(x+1)\big)+2=6||
-
Isoler le rapport tangente
||\begin{align}5\tan\big(\!-4(x+1)\big)+2&=6\\5\tan\big(\!-4(x+1)\big)&=4\\\tan\big(\!-4(x+1)\big)&=\dfrac{4}{5}\end{align}|| -
Déterminer l’angle trigonométrique
On détermine l’angle recherché en utilisant |\arctan.|||\begin{align}\tan\big(\!-4(x+1)\big)&=\dfrac{4}{5}\\&\Downarrow\\\boldsymbol{\color{#fa7921}{-4(x+1)}}&=\arctan\left(\dfrac{4}{5}\right)\\[3pt]&\approx\boldsymbol{\color{#fa7921}{0{,}67}}\end{align}||
-
Résoudre l’équation
On obtient l’équation suivante, formée par l’angle trouvé à l’étape précédente, qu’on résout.||\begin{align}-4(x+1)&\approx0{,}67\\x+1&\approx-0{,}17\\\boldsymbol{\color{#fa7921}{x_1}}&\approx\boldsymbol{\color{#fa7921}{-1{,}17}}\end{align}||
-
Calculer la période de la fonction tangente
Comme la fonction tangente est périodique, il faut calculer la période pour être en mesure de donner toutes les solutions.||\begin{align}p&=\dfrac{\pi}{\vert b\vert}\\[3pt]&=\dfrac{\pi}{\vert-4\vert}\\[3pt]&=\dfrac{\pi}{4}\end{align}||
-
Donner les solutions de l’équation
Puisqu’on cherche les solutions dans l’intervalle |\left[-\dfrac{3\pi}{2},-\dfrac{\pi}{2}\right],| il y a un nombre fini de solutions. On calcule les solutions en additionnant ou en soustrayant la période |\left(\dfrac{\pi}{4}\right)| à la valeur trouvée à l’étape 3, sans sortir de l’intervalle.
On rejette |-1{,}17,| car cette valeur est plus grande que |-\dfrac{\pi}{2}.|||\begin{align}x&\approx-1{,}17-\dfrac{\pi}{4}\\[3pt]&\approx-1{,}95\end{align}||On conserve |-1{,}95,| car cette valeur est dans l’intervalle |\left[-\dfrac{3\pi}{2},-\dfrac{\pi}{2}\right].|||\begin{align}x&\approx-1{,}95-\dfrac{\pi}{4}\\[3pt]&\approx-2{,}74\end{align}||On conserve |-2{,}74,| car cette valeur est dans l’intervalle |\left[-\dfrac{3\pi}{2},-\dfrac{\pi}{2}\right].|||\begin{align}x&\approx-2{,}74-\dfrac{\pi}{4}\\[3pt]&\approx-3{,}52\end{align}||On conserve |-3{,}52,| car cette valeur est dans l’intervalle |\left[-\dfrac{3\pi}{2},-\dfrac{\pi}{2}\right].|||\begin{align}x&\approx-3{,}52-\dfrac{\pi}{4}\\[3pt]&\approx-4{,}31\end{align}||On conserve |-4{,}31,| car cette valeur est dans l’intervalle |\left[-\dfrac{3\pi}{2},-\dfrac{\pi}{2}\right].|||\begin{align}x&\approx-4{,}31-\dfrac{\pi}{4}\\[3pt]&\approx-5{,}1\end{align}||On rejette |-5{,}1,| car cette valeur est plus petite que |-\dfrac{3\pi}{2}.|
Les solutions de l’équation |5\tan\big(\!-4(x+1)\big)+2=6| dans l’intervalle |\left[-\dfrac{3\pi}{2},-\dfrac{\pi}{2}\right]| sont donc les suivantes.||x\in\{-4{,}31;\,-3{,}52;\,-2{,}74;\,-1{,}95\}||
Voici un exemple où on résout une équation tangente de degré 2.
Résous l’équation suivante.||2\tan^2(x-2)-5\tan(x-2)+2=0||
On peut résoudre une équation tangente de ce type en utilisant les mêmes stratégies qu’on utilise pour résoudre une équation polynomiale de degré 2. Autrement dit, on peut utiliser la factorisation ou la formule quadratique.
Pour y arriver, il faut faire un changement de variable en remplaçant |\tan(x-2)| par |z.| De cette façon, on laisse temporairement de côté les rapports tangente afin de se concentrer sur la résolution du polynôme de degré 2.
On obtient alors l’équation suivante.||2\tan^2(x-2)-5\tan(x-2)+2=0\\\Updownarrow\\2z^2-5z+2=0||En utilisant la formule quadratique, on obtient les solutions suivantes pour |z.|||\begin{align}z_{1,2}&=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}\\[3pt]&=\dfrac{-(-5)\pm\sqrt{(-5)^2-4(2)(2)}}{2(2)}\\[3pt]&=\dfrac{5\pm\sqrt{9}}{4}\\\\z_1&=\dfrac{1}{2}\quad\text{et}\quad z_2=2\end{align}||Les solutions de l’équation |2z^2-5z+2=0| sont donc |z_1=\dfrac{1}{2}| et |z_2=2.| Puisqu’on a fait un changement de variable, on peut substituer |z| par |\tan(x-2).| On obtient alors 2 nouvelles équations.
||\tan(x-2)=\dfrac{1}{2}||
||\tan(x-2)=2||
On peut maintenant procéder comme on le ferait pour une équation tangente de degré 1.
-
Isoler le rapport tangente
Le rapport tangente est déjà isolé dans les 2 équations.
-
Déterminer les angles trigonométriques
On détermine les 2 angles recherchés en utilisant |\arctan| dans les 2 équations.
||\begin{align}\tan(x-2)&=\dfrac{1}{2}\\&\Downarrow\\\boldsymbol{\color{#fa7921}{x-2}}&=\arctan\left(\dfrac{1}{2}\right)\\[3pt]&\approx\boldsymbol{\color{#fa7921}{0{,}46}}\end{align}||
||\begin{align}\tan(x-2)&=2\\&\Downarrow\\\boldsymbol{\color{#51b6c2}{x-2}}&=\arctan(2)\\&\approx\boldsymbol{\color{#51b6c2}{1{,}11}}\end{align}||
-
Résoudre les équations
On obtient les 2 équations suivantes, formées par les angles trouvés à l’étape précédente, qu’on résout.
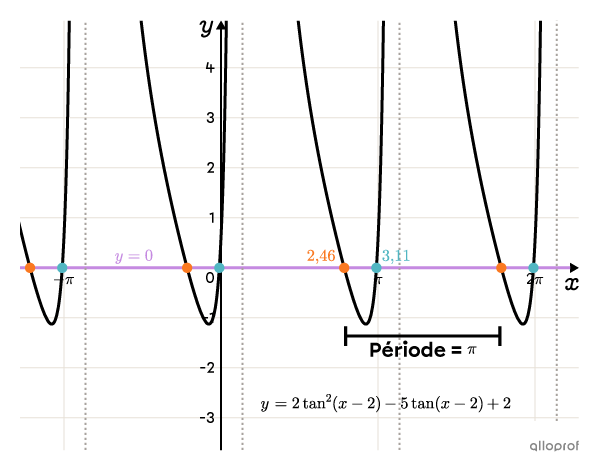
||\begin{align}x-2&\approx0{,}46\\\boldsymbol{\color{#fa7921}{x_1}}&\approx\boldsymbol{\color{#fa7921}{2{,}46}}\end{align}||
||\begin{align}x-2&\approx1{,}11\\\boldsymbol{\color{#51b6c2}{x_2}}&\approx\boldsymbol{\color{#51b6c2}{3{,}11}}\end{align}||
-
Calculer la période de la fonction tangente
Comme la fonction tangente est périodique, il faut calculer la période pour être en mesure de donner toutes les solutions.||\begin{align}p&=\dfrac{\pi}{\vert b\vert}\\[3pt]&=\dfrac{\pi}{\vert1\vert}\\[3pt]&=\pi\end{align}||
-
Donner les solutions de l’équation
Les solutions de l’équation |2\tan^2(x-2)-5\tan(x-2)+2=0| sont donc les suivantes.
||x\in\left\{2{,}46+\pi n;\ 3{,}11+\pi n\right\}||où||n\in\mathbb{Z}||
On peut représenter les solutions dans le graphique de la fonction tangente de degré 2 à l’aide d’un outil technologique. Tracer ce genre de graphique n’est pas au programme du secondaire.
La démarche à suivre pour résoudre une inéquation tangente est la suivante.
-
Changer le symbole d’inégalité par un symbole d’égalité.
-
Isoler le rapport tangente.
-
Déterminer l’angle trigonométrique à l’aide du tableau des valeurs remarquables ou de la fonction réciproque |\boldsymbol{\arctan}.|
-
Résoudre l’équation obtenue avec l’angle trigonométrique.
-
Calculer la période de la fonction tangente.
-
Calculer les asymptotes de la fonction tangente.
-
Donner l’ensemble-solution de l’inéquation.
Voici un exemple où on utilise le tableau des valeurs remarquables du rapport tangente pour résoudre l’inéquation.
Résous l'inéquation suivante.||3\tan\left(\dfrac{x}{4}\right)>-\sqrt{3}||
-
Changer le symbole d’inégalité par un symbole d’égalité
||\begin{align}3\tan\left(\dfrac{x}{4}\right)&>-\sqrt{3}\\&\downarrow\\3\tan\left(\dfrac{x}{4}\right)&=-\sqrt{3}\end{align}|| -
Isoler le rapport tangente
||\begin{align}3\tan\left(\dfrac{x}{4}\right)&=-\sqrt{3}\\[3pt]\tan\left(\dfrac{x}{4}\right)&=-\dfrac{\sqrt{3}}{3}\end{align}|| -
Déterminer l’angle trigonométrique
|
Angle |
Tangente de l’angle |
|---|---|
|
||\dfrac{\pi}{3}|| |
||\sqrt{3}|| |
|
||\dfrac{\pi}{4}|| |
||1|| |
|
||\dfrac{\pi}{6}|| |
||\dfrac{\sqrt{3}}{3}|| |
|
||0|| |
||0|| |
|
||\boldsymbol{\color{#fa7921}{-\dfrac{\pi}{6}}}|| |
||\boldsymbol{\color{#c58ae1}{-\dfrac{\sqrt{3}}{3}}}|| |
|
||-\dfrac{\pi}{4}|| |
||-1|| |
|
||-\dfrac{\pi}{3}|| |
||-\sqrt{3}|| |
Puisque |\boldsymbol{\color{#c58ae1}{-\dfrac{\sqrt{3}}{3}}}| est une valeur remarquable du rapport tangente, on détermine l’angle recherché directement à partir du tableau des valeurs remarquables.
On trouve que l’angle pour lequel le rapport tangente vaut |-\dfrac{\sqrt{3}}{3}| est |\boldsymbol{\color{#fa7921}{-\dfrac{\pi}{6}}}.|
-
Résoudre l’équation
||\begin{align}\tan\left(\dfrac{x}{4}\right)&=-\dfrac{\sqrt{3}}{3}\\ &\Downarrow\\\dfrac{x}{4}&=-\dfrac{\pi}{6}\\[3pt]\boldsymbol{\color{#fa7921}{x_1}}&=\boldsymbol{\color{#fa7921}{-\dfrac{2\pi}{3}}}\end{align}|| -
Calculer la période de la fonction tangente
Comme la fonction tangente est périodique, il faut calculer la période pour être en mesure de donner toutes les solutions.||\begin{align}p&=\dfrac{\pi}{\vert b\vert}\\[3pt]&=\dfrac{\pi}{\vert\frac{1}{4}\vert}\\[3pt]&=4\pi\end{align}||
-
Calculer les asymptotes de la fonction tangente
On calcule les asymptotes de part et d’autre de |\boldsymbol{\color{#fa7921}{x_1}}.|
Asymptote inférieure à |\boldsymbol{x_1}|
||\begin{align}\boldsymbol{\color{#333fb1}{x_0}}&=h-\dfrac{p}{2}\\[3pt]&=0-\dfrac{4\pi}{2}\\[3pt]&=\boldsymbol{\color{#333fb1}{-2\pi}}\end{align}||
Asymptote supérieure à |\boldsymbol{x_1}|
||\begin{align}\boldsymbol{\color{#ec0000}{x_2}}&=h+\dfrac{p}{2}\\[3pt]&=0+\dfrac{4\pi}{2}\\[3pt]&=\boldsymbol{\color{#ec0000}{2\pi}}\end{align}||
-
Donner l’ensemble-solution de l’inéquation
Il y a 2 intervalles possibles, soit celui entre l’asymptote inférieure |\boldsymbol{(\color{#333fb1}{x_0})}| et |\boldsymbol{\color{#fa7921}{x_1}},| et celui entre |\boldsymbol{\color{#fa7921}{x_1}}| et l’asymptote supérieure |\boldsymbol{(\color{#ec0000}{x_2})}.| Pour déterminer l’intervalle qui fait partie de l’ensemble-solution, on peut utiliser le graphique ou tester une valeur de |x| dans chaque intervalle.
Remarque : Puisque le signe d'inégalité est |>,| la borne associée à |\boldsymbol{\color{#fa7921}{x_1}}| est exclue de l’ensemble-solution. De plus, la borne associée à une asymptote est toujours exclue.
||\left]\boldsymbol{\color{#333fb1}{-2\pi}},\boldsymbol{\color{#fa7921}{-\dfrac{2\pi}{3}}}\right[||On teste |x=-\pi.|||\begin{align}3\tan\left(\dfrac{x}{4}\right)&>-\sqrt{3}\\[3pt]3\tan\left(\dfrac{-\pi}{4}\right)&\overset{\text{?}}{>}-\sqrt{3}\\3\times-1&\overset{\text{?}}{>}-\sqrt{3}\\-3&\color{#ec0000}{\not>}-\sqrt{3}\end{align}||Cette inégalité est fausse, ce qui implique que l’intervalle |\left]\boldsymbol{\color{#333fb1}{-2\pi}},\boldsymbol{\color{#fa7921}{-\dfrac{2\pi}{3}}}\right[| ne fait pas partie de l’ensemble-solution.
||\left]\boldsymbol{\color{#fa7921}{-\dfrac{2\pi}{3}}},\boldsymbol{\color{#ec0000}{2\pi}}\right[||On teste |x=0.|||\begin{align}3\tan\left(\dfrac{x}{4}\right)&>-\sqrt{3}\\[3pt]3\tan\left(\dfrac{0}{4}\right)&\overset{\text{?}}{>}-\sqrt{3}\\3\times0&\overset{\text{?}}{>}-\sqrt{3}\\0&>-\sqrt{3}\end{align}||Cette inégalité est vraie, ce qui implique que l’intervalle |\left]\boldsymbol{\color{#fa7921}{-\dfrac{2\pi}{3}}},\boldsymbol{\color{#ec0000}{2\pi}}\right[| fait partie de l’ensemble-solution.
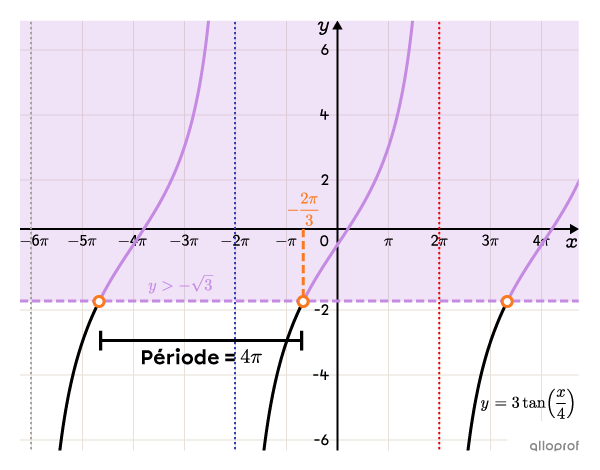
Puisque les bornes de l’intervalle se répètent à chaque période, l’ensemble-solution de l’inéquation |3\tan\left(\dfrac{x}{4}\right)>-\sqrt{3}| est le suivant.
||x\in\left]-\dfrac{2\pi}{3}+4\pi n,\ 2\pi+4\pi n\right[||où||n\in\mathbb{Z}||
Voici un exemple où on utilise la fonction réciproque arc tangente pour résoudre l’inéquation.
Résous l’inéquation suivante.||\dfrac{1}{4}\tan\big(2(x-\pi)\big)-6\le-5||
Résous l’inéquation suivante.||\dfrac{1}{4}\tan\big(2(x-\pi)\big)-6\le-5||
-
Changer le symbole d’inégalité par un symbole d’égalité
||\begin{align}\dfrac{1}{4}\tan\big(2(x-\pi)\big)-6&\le-5\\&\downarrow\\\dfrac{1}{4}\tan\big(2(x-\pi)\big)-6&=-5\end{align}|| -
Isoler le rapport tangente
||\begin{align}\dfrac{1}{4}\tan\big(2(x-\pi)\big)-6&=-5\\[3pt]\dfrac{1}{4}\tan\big(2(x-\pi)\big)&=1\\[3pt]\tan\big(2(x-\pi)\big)&=4\end{align}|| -
Déterminer l’angle trigonométrique
On détermine l’angle recherché en utilisant |\arctan.|||\begin{align}\tan\big(2(x-\pi)\big)&=4\\&\Downarrow\\\boldsymbol{\color{#fa7921}{2(x-\pi)}}&=\arctan\left(4\right)\\&\approx\boldsymbol{\color{#fa7921}{1{,}33}}\end{align}||
-
Résoudre l’équation
||\begin{align}2(x-\pi)&\approx1{,}33\\x-\pi&\approx0{,}66\\\boldsymbol{\color{#fa7921}{x_1}}&\approx\boldsymbol{\color{#fa7921}{3{,}8}}\end{align}|| -
Calculer la période de la fonction tangente
Comme la fonction tangente est périodique, il faut calculer la période pour être en mesure de donner toutes les solutions.||\begin{align}p&=\dfrac{\pi}{\vert b\vert}\\[3pt]&=\dfrac{\pi}{\vert2\vert}\\[3pt]&=\dfrac{\pi}{2}\end{align}||
-
Calculer les asymptotes de la fonction tangente
On calcule les asymptotes de part et d’autre de |\boldsymbol{\color{#fa7921}{x_1}}.|
Asymptote inférieure à |\boldsymbol{x_1}|
||\begin{align}\boldsymbol{\color{#333fb1}{x_0}}&=h-\dfrac{p}{2}\\[3pt]&=\pi-\dfrac{\frac{\pi}{2}}{2}\\[3pt]&=\pi-\dfrac{\pi}{4}\\[3pt]&=\boldsymbol{\color{#333fb1}{\dfrac{3\pi}{4}}}\end{align}||
Asymptote supérieure à |\boldsymbol{x_1}|
||\begin{align}\boldsymbol{\color{#ec0000}{x_2}}&=h+\dfrac{p}{2}\\[3pt]&=\pi+\dfrac{\frac{\pi}{2}}{2}\\[3pt]&=\pi+\dfrac{\pi}{4}\\[3pt]&=\boldsymbol{\color{#ec0000}{\dfrac{5\pi}{4}}}\end{align}||
-
Donner l’ensemble-solution de l’inéquation
Il y a 2 intervalles possibles, soit celui entre l’asymptote inférieure |\boldsymbol{(\color{#333fb1}{x_0})}| et |\boldsymbol{\color{#fa7921}{x_1}},| et celui entre |\boldsymbol{\color{#fa7921}{x_1}}| et l’asymptote supérieure |\boldsymbol{(\color{#ec0000}{x_2})}.| Pour déterminer l’intervalle qui fait partie de l’ensemble-solution, on peut utiliser le graphique ou tester une valeur de |x| dans chaque intervalle.
Remarque : Puisque le signe d'inégalité est |\le,| la borne associée à |\boldsymbol{\color{#fa7921}{x_1}}| est incluse dans l’ensemble-solution. De plus, la borne associée à une asymptote est toujours exclue.
||\left]\boldsymbol{\color{#333fb1}{\dfrac{3\pi}{4}}};\boldsymbol{\color{#fa7921}{3{,}8}}\right]||On teste |x=\pi.|||\begin{align}\dfrac{1}{4}\tan\big(2(x-\pi)\big)-6&\le-5\\[3pt]\dfrac{1}{4}\tan\big(2(\pi-\pi)\big)-6&\overset{\text{?}}{\le}-5\\[3pt]\dfrac{1}{4}\tan(0)-6&\overset{\text{?}}{\le}-5\\[3pt]\dfrac{1}{4}\times0-6&\overset{\text{?}}{\le}-5\\[3pt]-6&\le-5\end{align}||Cette inégalité est vraie, ce qui implique que l’intervalle |\left]\boldsymbol{\color{#333fb1}{\dfrac{3\pi}{4}}};\boldsymbol{\color{#fa7921}{3{,}8}}\right]| fait partie de l’ensemble-solution.
||\left[\boldsymbol{\color{#fa7921}{3{,}8}};\boldsymbol{\color{#ec0000}{\dfrac{5\pi}{4}}}\right[||On teste |x=3{,}85.|||\begin{align}\dfrac{1}{4}\tan\big(2(x-\pi)\big)-6&\le-5\\[3pt]\dfrac{1}{4}\tan\big(2(3{,}85-\pi)\big)-6&\overset{\text{?}}{\le}-5\\[3pt]\dfrac{1}{4}\times6{,}44-6&\overset{\text{?}}{\le}-5\\[3pt]-4{,}39&\color{#ec0000}{\not\le}-5\end{align}||Cette inégalité est fausse, ce qui implique que l’intervalle |\left[\boldsymbol{\color{#fa7921}{3{,}8}};\boldsymbol{\color{#ec0000}{\dfrac{5\pi}{4}}}\right[| ne fait pas partie de l’ensemble-solution.
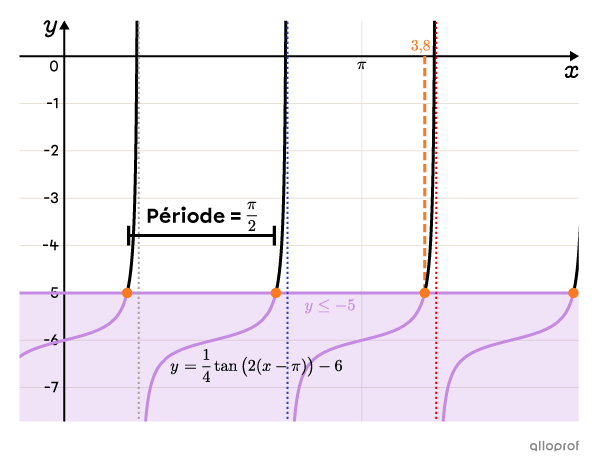
Puisque les bornes de l’intervalle se répètent à chaque période, l’ensemble-solution de l’inéquation |\dfrac{1}{4}\tan\big(2(x-\pi)\big)-6\le-5| est le suivant.
||x\in\left]\dfrac{3\pi}{4}+\dfrac{\pi}{2}n;\ 3{,}8+\dfrac{\pi}{2}n\right]||où||n\in\mathbb{Z}||
Voici un exemple où on résout une inéquation tangente de degré 2.
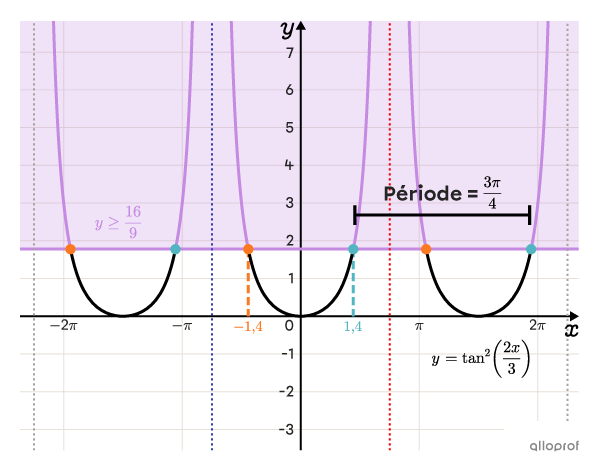
Résous l'inéquation suivante.||\tan^2\left(\dfrac{2x}{3}\right)\ge\dfrac{16}{9}||
-
Changer le symbole d’inégalité par un symbole d’égalité
||\begin{align}\tan^2\left(\dfrac{2x}{3}\right)&\ge\dfrac{16}{9}\\&\downarrow\\\tan^2\left(\dfrac{2x}{3}\right)&=\dfrac{16}{9}\end{align}|| -
Isoler le rapport tangente
||\begin{align}\tan^2\left(\dfrac{2x}{3}\right)&=\dfrac{16}{9}\\[3pt]\tan\left(\dfrac{2x}{3}\right)&=\pm\sqrt{\dfrac{16}{9}}\\[3pt]\tan\left(\dfrac{2x}{3}\right)&=\pm\dfrac{4}{3}\end{align}|| -
Déterminer les angles trigonométriques
On détermine les 2 angles recherchés en utilisant |\arctan| dans les 2 équations.
||\begin{align}\tan\left(\dfrac{2x}{3}\right)&=-\dfrac{4}{3}\\&\Downarrow\\\boldsymbol{\color{#fa7921}{\dfrac{2x}{3}}}&=\arctan\left(-\dfrac{4}{3}\right)\\[3pt]&\approx\boldsymbol{\color{#fa7921}{-0{,}93}}\end{align}||
||\begin{align}\tan\left(\dfrac{2x}{3}\right)&=\dfrac{4}{3}\\&\Downarrow\\\boldsymbol{\color{#51b6c2}{\dfrac{2x}{3}}}&=\arctan\left(\dfrac{4}{3}\right)\\[3pt]&\approx\boldsymbol{\color{#51b6c2}{0{,}93}}\end{align}||
-
Résoudre les équations
On obtient les 2 équations suivantes, formées par les angles trouvés à l’étape précédente, qu’on résout.
||\begin{align}\dfrac{2x}{3}&\approx-0{,}93\\[3pt]\boldsymbol{\color{#fa7921}{x_1}}&\approx\boldsymbol{\color{#fa7921}{-1{,}39}}\end{align}||
||\begin{align}\dfrac{2x}{3}&\approx0{,}93\\[3pt]\boldsymbol{\color{#51b6c2}{x_2}}&\approx\boldsymbol{\color{#51b6c2}{1{,}39}}\end{align}||
-
Calculer la période de la fonction tangente
Comme la fonction tangente est périodique, il faut calculer la période pour être en mesure de donner toutes les solutions.||\begin{align}p&=\dfrac{\pi}{\vert b\vert}\\[3pt]&=\dfrac{\pi}{\left\vert\frac{2}{3}\right\vert}\\[3pt]&=\dfrac{3\pi}{2}\end{align}||
-
Calculer les asymptotes de la fonction tangente
On calcule les asymptotes de part et d’autre de |\boldsymbol{\color{#fa7921}{x_1}}| et |\boldsymbol{\color{#51b6c2}{x_2}}.|
Asymptote inférieure à |\boldsymbol{x_1}|
||\begin{align}\boldsymbol{\color{#333fb1}{x_0}}&=h-\dfrac{p}{2}\\[3pt]&=0-\dfrac{\frac{3\pi}{2}}{2}\\[3pt]&=\boldsymbol{\color{#333fb1}{-\dfrac{3\pi}{4}}}\end{align}||
Asymptote supérieure à |\boldsymbol{x_2}|
||\begin{align}\boldsymbol{\color{#ec0000}{x_3}}&=h+\dfrac{p}{2}\\[3pt]&=0+\dfrac{\frac{3\pi}{2}}{2}\\[3pt]&=\boldsymbol{\color{#ec0000}{\dfrac{3\pi}{4}}}\end{align}||
-
Donner l’ensemble-solution de l’inéquation
Il y a 3 intervalles possibles, soit celui entre l’asymptote inférieure |\boldsymbol{(\color{#333fb1}{x_0})}| et |\boldsymbol{\color{#fa7921}{x_1}},| celui entre |\boldsymbol{\color{#fa7921}{x_1}}| et |\boldsymbol{\color{#51b6c2}{x_2}},| et celui entre |\boldsymbol{\color{#51b6c2}{x_2}}| et l’asymptote supérieure |\boldsymbol{(\color{#ec0000}{x_3})}.| Pour déterminer le ou les intervalles qui font partie de l’ensemble-solution, on peut utiliser le graphique ou tester une valeur de |x| dans chaque intervalle.
Remarque : Puisque le signe d'inégalité est |\ge,| la borne associée à |\boldsymbol{\color{#fa7921}{x_1}}| et la borne associée à |\boldsymbol{\color{#51b6c2}{x_2}}| sont incluses dans l’ensemble-solution. De plus, la borne associée à une asymptote est toujours exclue.
||\left]\boldsymbol{\color{#333fb1}{-\dfrac{3\pi}{4}}};\boldsymbol{\color{#fa7921}{-1{,}39}}\right]||On teste |x=-\dfrac{\pi}{2}.|||\begin{align}\tan^2\left(\dfrac{2x}{3}\right)&\ge\dfrac{16}{9}\\[3pt]\tan^2\left(\dfrac{2\times-\frac{\pi}{2}}{3}\right)&\overset{\text{?}}{\ge}\dfrac{16}{9}\\[3pt]\tan^2\left(-\dfrac{\pi}{3}\right)&\overset{\text{?}}{\ge}\dfrac{16}{9}\\[3pt](-\sqrt{3})^2&\overset{\text{?}}{\ge}\dfrac{16}{9}\\[3pt]3&\ge\dfrac{16}{9}\end{align}||Cette inégalité est vraie, ce qui implique que l’intervalle |\left]\boldsymbol{\color{#333fb1}{-\dfrac{3\pi}{4}}};\boldsymbol{\color{#fa7921}{-1{,}39}}\right]| fait partie de l’ensemble-solution.
||[\boldsymbol{\color{#fa7921}{-1{,}39}};\boldsymbol{\color{#51b6c2}{1{,}39}}]||On teste |x=0.|||\begin{align}\tan^2\left(\dfrac{2x}{3}\right)&\ge\dfrac{16}{9}\\[3pt]\tan^2\left(\dfrac{2\times0}{3}\right)&\overset{\text{?}}{\ge}\dfrac{16}{9}\\[3pt]\tan^2(0)&\overset{\text{?}}{\ge}\dfrac{16}{9}\\[3pt]0^2&\overset{\text{?}}{\ge}\dfrac{16}{9}\\[3pt]0&\color{#ec0000}{\not\ge}\dfrac{16}{9}\end{align}||Cette inégalité est fausse, ce qui implique que l’intervalle |[\boldsymbol{\color{#fa7921}{-1{,}39}};\boldsymbol{\color{#51b6c2}{1{,}39}}]| ne fait pas partie de l’ensemble-solution.
||\left[\boldsymbol{\color{#51b6c2}{1{,}39}};\boldsymbol{\color{#ec0000}{\dfrac{3\pi}{4}}}\right[||On teste |x=\dfrac{\pi}{2}.|||\begin{align}\tan^2\left(\dfrac{2x}{3}\right)&\ge\dfrac{16}{9}\\[3pt]\tan^2\left(\dfrac{2\times\frac{\pi}{2}}{3}\right)&\overset{\text{?}}{\ge}\dfrac{16}{9}\\[3pt]\tan^2\left(\dfrac{\pi}{3}\right)&\overset{\text{?}}{\ge}\dfrac{16}{9}\\[3pt]\sqrt{3}^2&\overset{\text{?}}{\ge}\dfrac{16}{9}\\[3pt]3&\ge\dfrac{16}{9}\end{align}||Cette inégalité est vraie, ce qui implique que l’intervalle |\left[\boldsymbol{\color{#51b6c2}{1{,}39}};\boldsymbol{\color{#ec0000}{\dfrac{3\pi}{4}}}\right[| fait partie de l’ensemble-solution.
Puisque les bornes des intervalles se répètent à chaque période, l’ensemble-solution de l’inéquation |\tan^2\left(\dfrac{2x}{3}\right)\ge\dfrac{16}{9}| est le suivant.
||x\in\left]-\dfrac{3\pi}{4}+\dfrac{3\pi}{2}n;\,-1{,}39+\dfrac{3\pi}{2}n\right]\ \cup\ \left[1{,}39+\dfrac{3\pi}{2}n;\ \dfrac{3\pi}{4}+\dfrac{3\pi}{2}n\right[||où||n\in\mathbb{Z}||
On peut représenter l’ensemble-solution dans le graphique de la fonction tangente de degré 2 à l’aide d’un outil technologique. Tracer ce genre de graphique n’est pas au programme du secondaire.