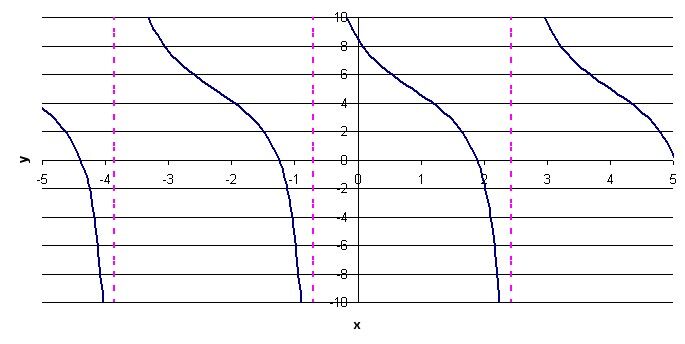
Il est possible de tracer une fonction tangente dans un plan cartésien si on connait sa règle. Pour ce faire, on peut suivre les étapes suivantes :
-
Placer le point d'inflexion |(h,k).|
-
Trouver la période de la fonction |\left(\text{période}=\dfrac{\pi}{{\mid}b{\mid}}\right).|
-
Calculer les équations des asymptotes situées à gauche et à droite du point d’inflexion déjà placé |\left(x=h\pm\dfrac{\text{période}}{2}\right)| et tracer ces 2 asymptotes.
-
Déterminer si la fonction est croissante |(ab>0)| ou décroissante |(ab<0).|
-
Positionner quelques points supplémentaires, au besoin.
-
Tracer la fonction.
Trace le graphique de la fonction |f(x)=2\tan\big(3(x-1)\big)+4.|
1. Placer le point d’inflexion
Les coordonnées du point d'inflexion sont |(h,k)=(1,4).|

2. Trouver la période de la fonction
La période de la fonction se calcule ainsi : ||p = \dfrac{\pi}{{\mid}b{\mid}} = \dfrac{\pi}{{\mid} 3 {\mid} } = \dfrac{\pi}{3}||
3. Calculer les équations des asymptotes situées à gauche et à droite du point d’inflexion déjà placé et tracer ces 2 asymptotes
L'équation de l'asymptote à gauche du point |(h,k)| se calcule ainsi : ||x = 1 - \dfrac{\dfrac{\pi}{3}}{2} = 1-\dfrac{\pi}{6} = \dfrac{6-\pi}{6}||
L'équation de l'asymptote à droite du point |(h,k)| se calcule ainsi : || x = 1 + \dfrac{\dfrac{\pi}{3}}{2} = 1+\dfrac{\pi}{6}= \dfrac{6+\pi}{6}||

4. Déterminer si la fonction est croissante ou décroissante
Le produit |ab| est positif, la fonction est donc croissante. En effet, |2 \times 3 >0.|
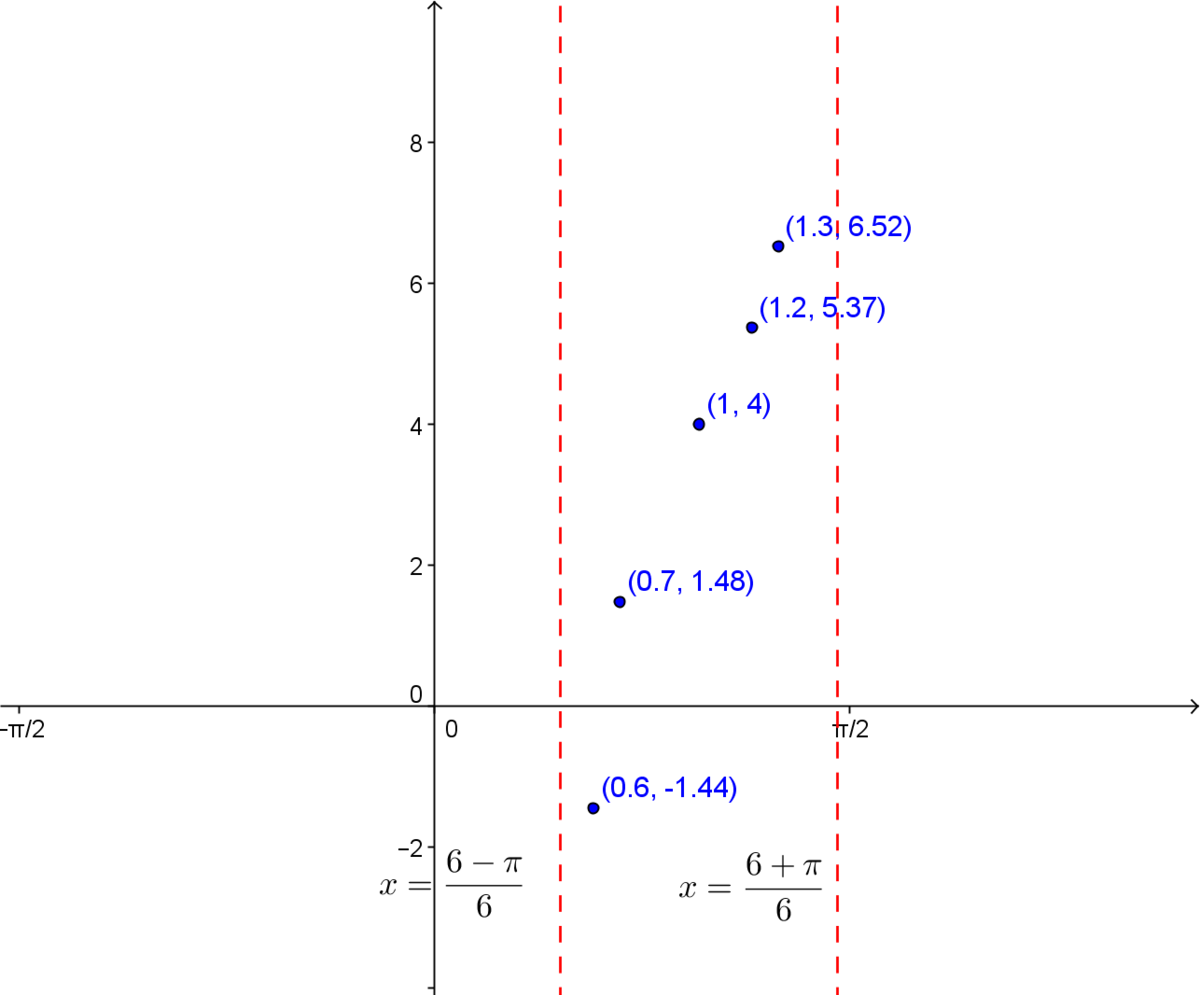
5. Positionner quelques points supplémentaires, au besoin
Pour trouver d'autres points, on peut faire une table de valeurs.
| |x| | |y| |
|---|---|
| |0{,}6| | |-1{,}14| |
| |0{,}7| | |1{,}48| |
| |1{,}2| | |5{,}37| |
| |1{,}3| | |6{,}52| |
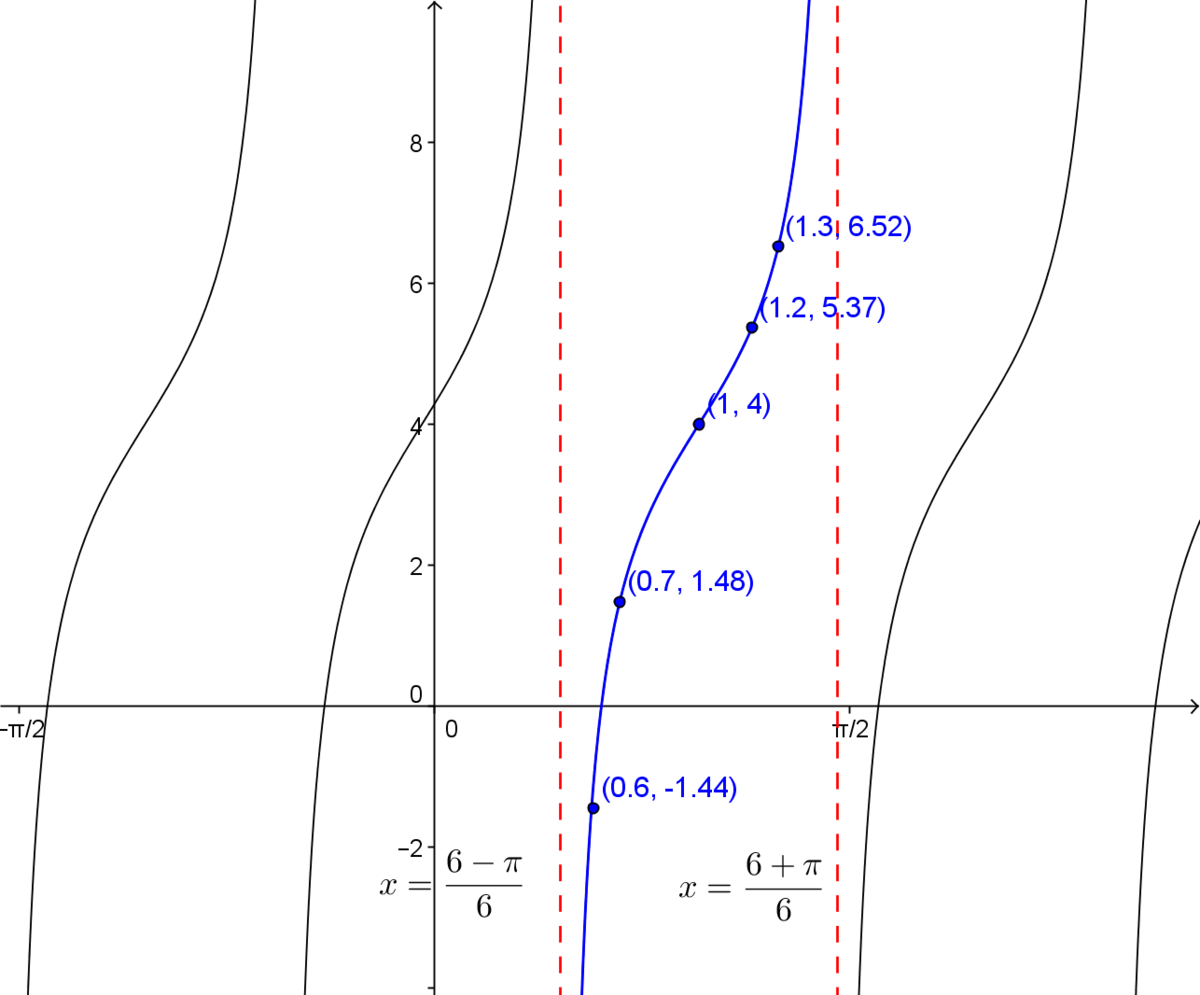
6. Tracer la fonction
Il existe une seconde manière de tracer une fonction tangente transformée dans un plan cartésien à l'aide de sa règle en utilisant les paramètres |a,| |b,| |h| et |k|. Pour ce faire, on peut suivre les étapes suivantes :
-
Tracer la fonction tangente de base, c'est-à-dire |y = \tan(x).|
-
Appliquer à cette fonction de base le changement d'échelle vertical imposé par le paramètre |a.|
-
Appliquer le changement d'échelle horizontal imposé par le paramètre |b.|
-
Appliquer la translation horizontale imposée par le paramètre |h.|
-
Appliquer la translation verticale imposée par le paramètre |k.|
Remarque : Les quatre dernières étapes peuvent être effectuées dans n'importe quel ordre.
Tracez la courbe |y = -3 \tan \big(1(x - 4)\big) + 5| dans un plan cartésien.
1. Tracer la fonction tangente de base.
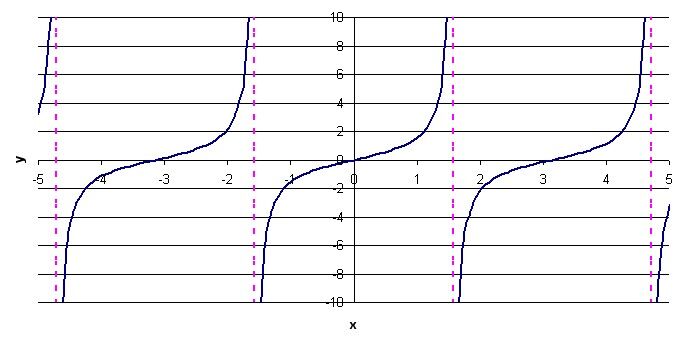
2. Appliquer le changement imposé par le paramètre |a|
Le paramètre |a| est égal à -3. Il faut donc effectuer une réflexion par rapport à l'axe des abscisses et « étirer » verticalement la fonction d'un facteur 3. On obtient la fonction suivante :
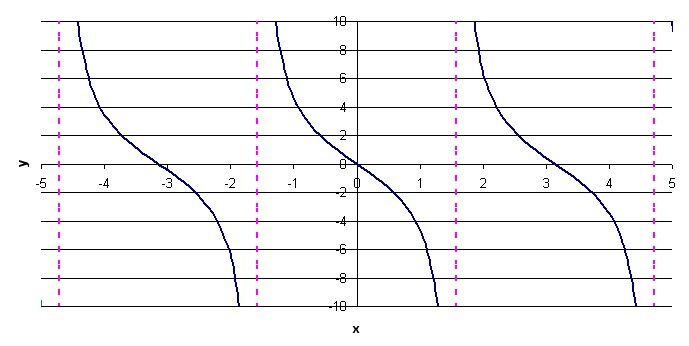
3. Appliquer le changement imposé par le paramètre |b|
Dans ce cas-ci, le paramètre |b| est égal à 1. Il n'est pas nécessaire d'effectuer de changement d'échelle horizontale.
4. Appliquer le changement imposé par le paramètre |h|
Dans ce cas-ci, le paramètre |h| est égal à 4. Il faudra donc effectuer une translation de quatre unités vers la droite :
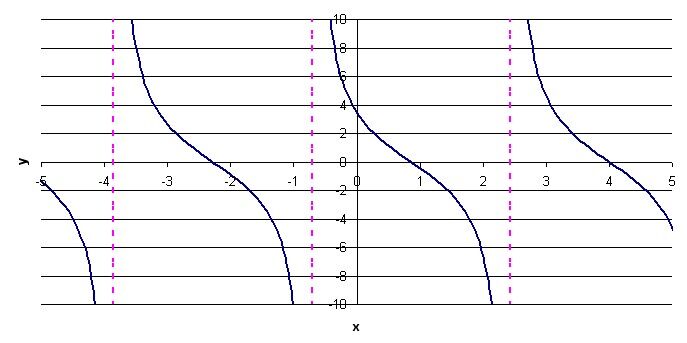
5. Appliquer le changement imposé par le paramètre |k|
Dans ce cas-ci, le paramètre |k| est égal à 5. Il faudra donc effectuer une translation de cinq unités vers le haut :