La radioactivité est le phénomène lors duquel le noyau d’un atome instable se dégrade en émettant des particules et/ou des radiations hautement énergétiques.
Lorsqu’un atome dont le noyau est instable se désintègre, une transformation nucléaire se produit. Cette transformation permet au noyau de l’atome de se stabiliser. Cette stabilisation est accompagnée d’un ou de plusieurs types de rayonnement : le rayonnement alpha |(\alpha),| le rayonnement bêta |(\beta)| et le rayonnement gamma |(\gamma).|
Les applications et les impacts de la radioactivité sont très variés. On peut exploiter la radioactivité des atomes pour dater des objets anciens, pour générer de l’énergie, pour élaborer des traitements médicaux, etc. Évaluer la demi-vie d’un atome donné peut fournir une indication de sa capacité à se désintégrer et du type d’utilisation qu’on peut en faire.
La radioactivité est un phénomène naturel qui a été découvert en 1896 par le physicien Henri Becquerel. La radioactivité d’une substance peut se mesurer de plusieurs manières. Par exemple, on peut employer le becquerel par gramme |(\text{Bq/g}).| Cette unité, nommée en l’honneur d’Henri Becquerel, permet d’évaluer le nombre de désintégrations d’atomes par seconde pour chaque gramme de matière qui se désintègre. C’est ce qu’on appelle l’activité massique.
Le tableau suivant permet de comparer la radioactivité de sources diverses.
| Source | Activité massique approximative |(\text{Bq/g})| |
|---|---|
| Corps humain | |0{,}120| |
| Banane | |0{,}110| |
| Eau de mer | |0{,}013| |
| Minerai d'uranium | |10\ 000| |
| Plutonium 239 | |2\ 300\ 000\ 000| |
Source des données : Institut de radioprotection et de sûreté nucléaire, 2021.
Les rayonnements alpha |(\alpha)| et bêta |(\beta)| sont des particules. Ce n’est pas le cas du rayonnement gamma |(\gamma)| qui est plutôt de nature électromagnétique. Ces propriétés ont une influence sur la capacité de ces rayonnements à pénétrer la matière. Ainsi, les rayonnements |\gamma| ont une capacité de pénétration plus grande que les particules |\alpha| et |\beta.| Les particules |\beta,| qui sont significativement plus petites et plus légères que les particules |\alpha,| sont plus pénétrantes que ces dernières.
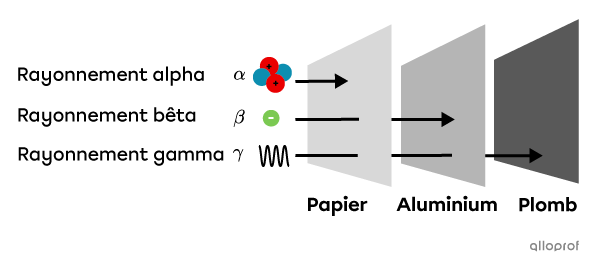
Le schéma suivant résume la capacité de pénétration des différents types de rayonnements.
-
Les rayonnements |\alpha| n’ont pas la capacité de pénétrer une feuille de papier. Ils ne peuvent pas non plus traverser la peau.
-
Les rayonnements |\beta| peuvent traverser une feuille de papier, mais pas une feuille d’aluminium. De plus, ils peuvent pénétrer le corps de façon superficielle et ne représentent qu’un faible risque pour la santé.
-
Les rayonnements |\gamma| peuvent pénétrer le papier et l’aluminium, mais peuvent être absorbés par le plomb. Ils peuvent également traverser le corps et représenter un grand risque pour la santé.
Ces trois types de rayonnement sont hautement énergétiques. On les appelle également rayonnements ionisants, car ils ont la capacité de créer des ions lorsqu’ils pénètrent la matière. En fonction de la façon dont ces rayons ionisants sont exploités, ils peuvent être bénéfiques ou dangereux pour la santé humaine.
La tomographie par émission de positons (TEP) exploite les rayons gamma. Elle permet de générer des images qui seront utiles aux médecins pour élaborer leur diagnostic.
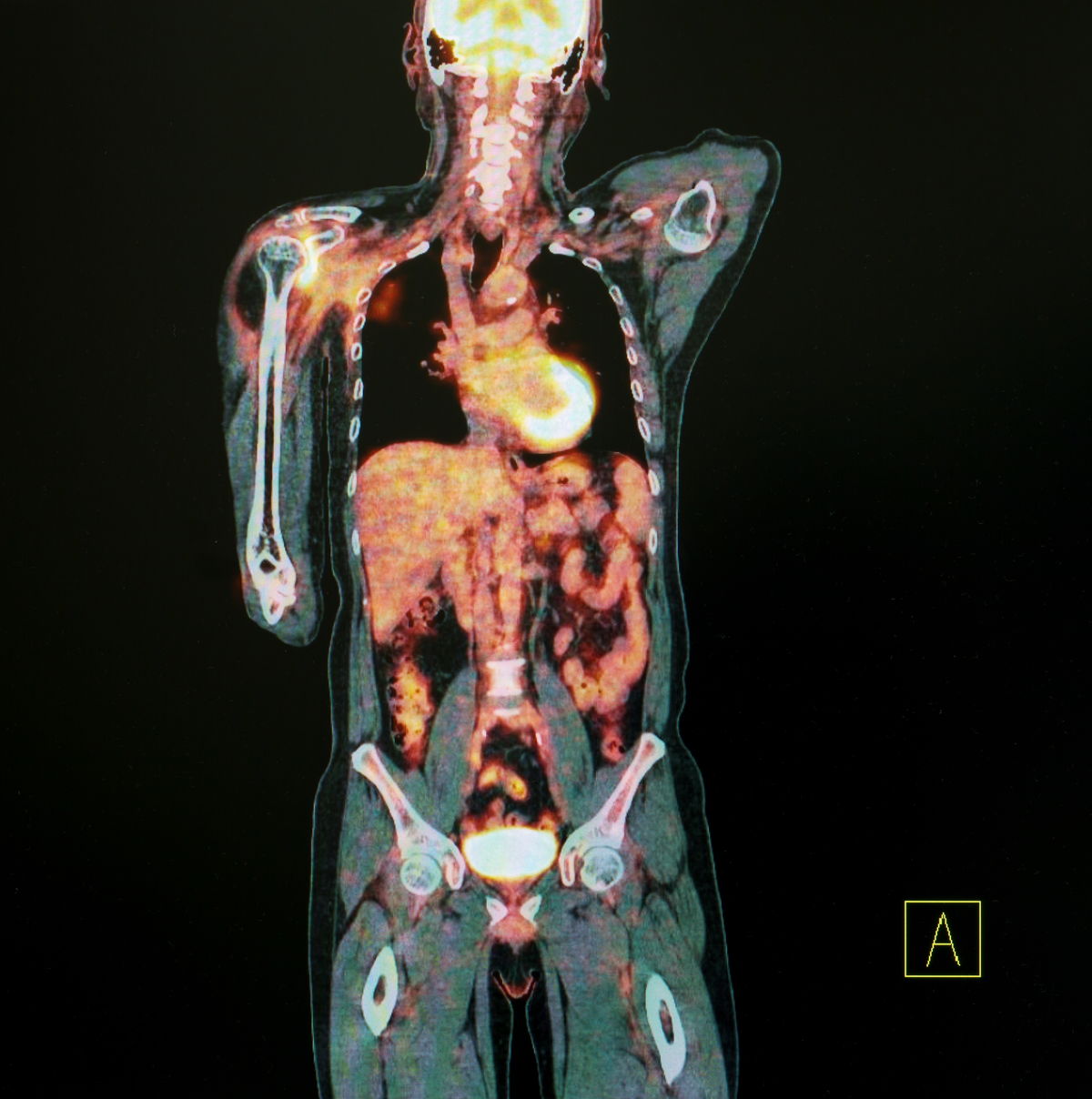
Monet_3k, Shutterstock.com
Les rayonnements gamma peuvent être exploités dans les traitements de radiothérapie. Ils ont la capacité de détruire les tissus cancéreux. Par exemple, le couteau gamma est une machine qui permet de détruire les tumeurs du cerveau avec beaucoup de précision.
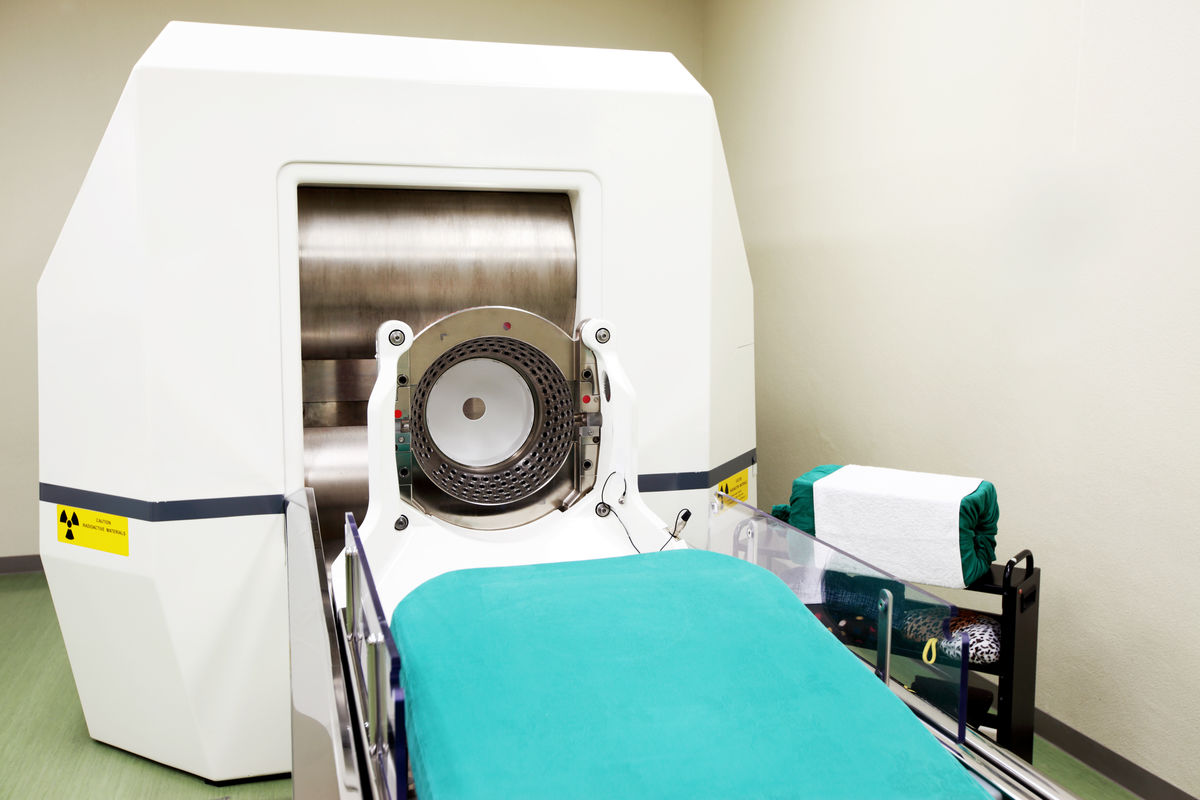
Alexander Gatsenko, Shutterstock.com
Les catastrophes nucléaires de Tchernobyl en Ukraine (1986) et de Fukushima au Japon (2011) sont les plus graves de l’histoire. Elles ont provoqué la libération d’une grande quantité de rayonnements radioactifs. Ces rayonnements ont fait de nombreuses victimes en engendrant des mutations génétiques qui ont causé des cancers et des malformations infantiles. De plus, les sols, l’air et les cours d’eau ont été largement contaminés.

Presslab, Shutterstock.com
Le temps de demi-vie |(t_{1/2})| d’un isotope correspond au temps nécessaire pour que la moitié des atomes présents dans un échantillon se dégrade.
Le temps de demi-vie est un indicatif de la stabilité d’un isotope.
Si un isotope est très instable, il faudra peu de temps pour que la moitié des atomes d’un échantillon de cet isotope se dégrade. Le temps de demi-vie sera court. Par exemple, le bohrium 271 |(^{271}\text{Bh})| est très instable et son temps de demi-vie est de |1{,}2| seconde.
Si, au contraire, un isotope est très stable, il faudra beaucoup de temps pour que la moitié des atomes d’un échantillon de cet isotope se dégrade. Le temps de demi-vie sera long. C’est le cas de l’iode 129 |(^{129}\text{I})| dont le temps de demi-vie est de |15{,}7| millions d’années.
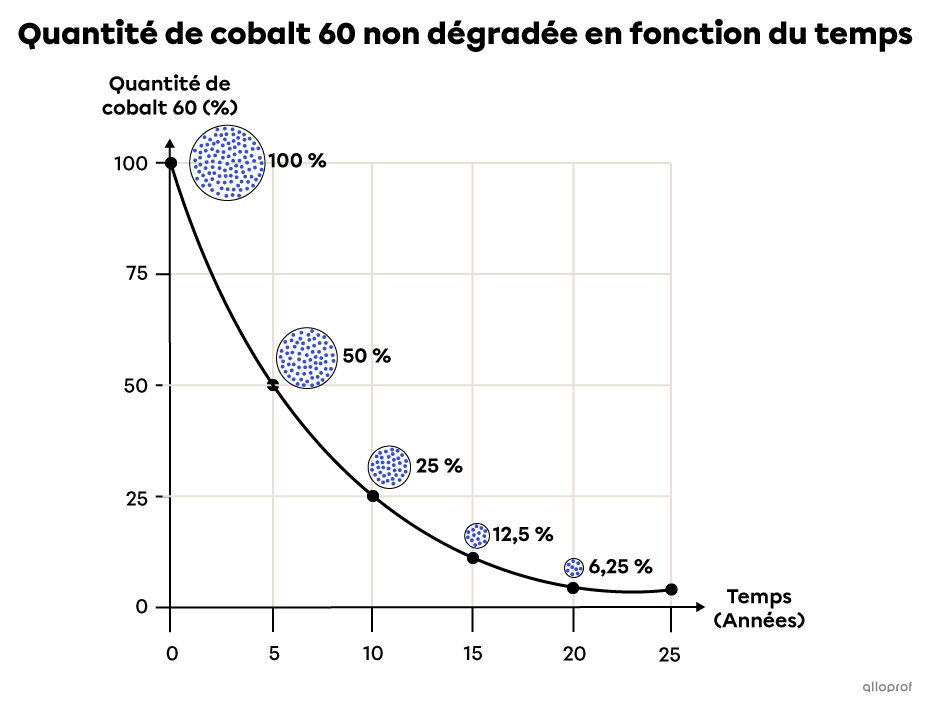
Ce graphique présente la quantité de cobalt 60 non dégradée en fonction du temps. Le graphique montre qu’au bout d’environ 5 ans, 50 % de l’échantillon de cobalt est dégradé. Le temps de demi-vie du cobalt 60 est donc approximativement de 5 ans. Il reste alors 50 % de l’échantillon initial.
Il faudra 5 autres années pour dégrader la moitié de ce qu’il reste, soit 25 % de cobalt, puis encore 5 autres années pour dégrader la moitié des 25 % restants, et ainsi de suite.
L’exploitation des mines d’uranium engendre plusieurs types de déchets radioactifs tels que le radium 226 |(^{226}\text{Ra}),| le thorium 230 |(^{230}\text{Th}),| divers isotopes du baryum |(\text{Ba})| et bien d’autres. La demi-vie de ces isotopes peut varier de quelques secondes à plusieurs milliers d’années, ce qui représente un défi pour l’entreposage sécuritaire de ces déchets.

John Carnemolla, Shutterstock.com
La notion de demi-vie peut également être exploitée afin de dater les spécimens archéologiques. Pour cela, on peut exploiter de nombreux éléments tels que le carbone, l’uranium ou encore le plomb.
Le carbone qui se trouve sur notre planète se trouve notamment sous la forme de carbone 12 |(^{12}_{6}\text{C}),| mais comprend aussi d’autres isotopes en petite quantité comme le carbone 13 |(^{13}_{6}\text{C})| et le carbone 14 |(^{14}_{6}\text{C}).| C’est ce dernier isotope qui est exploité afin d’effectuer la datation au carbone 14 de spécimens comprenant du carbone.
Lorsqu’un organisme est vivant, la concentration de carbone 14 qui le compose est stable. Par contre, lorsqu’un organisme décède, sa concentration de carbone 14 diminue avec le temps. Puisqu’on sait que le temps de demi-vie du carbone 14 est d’environ 5 730 années, l’âge de certains spécimens archéologiques peut être déterminé.
Par exemple, si la concentration de carbone 14 des restes d’un animal est deux fois plus petite que la normale, on sait qu’une demi-vie s’est écoulée depuis son décès. Cet animal aurait donc vécu il y a environ 5 730 années.

Dtopal, Shutterstock.com
On peut représenter les particules |\alpha| de diverses manières.
| |^4_2\text{He}^{2+}| | |^4_2\text{He}| | |\alpha| | |^4_2\alpha| |
Les particules |\alpha| sont généralement émises lorsqu’un atome dont le noyau est trop lourd se dégrade pour engendrer un atome dont le noyau est plus léger. À l’aide de la notation A/Z, aussi appelée notation de Berzelius, on peut représenter ce type de transformation de la manière suivante.
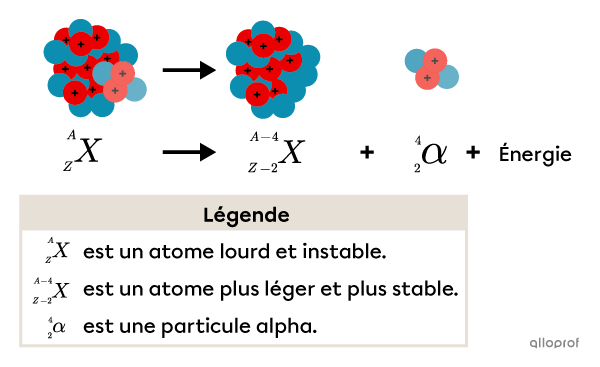
L’émission de rayonnements |\alpha| engendre les modifications suivantes :
-
l’atome qui se désintègre perd 2 neutrons et 2 protons;
-
son numéro atomique |(Z)| diminue de 2;
-
son nombre de masse |(A)| diminue de 4;
-
en bref, l’atome produit lors de cette réaction nucléaire est plus léger et plus stable grâce à un ratio plus favorable entre le nombre de protons et de neutrons.
En 1903, Marie Curie a reçu le prix Nobel de physique pour ses recherches sur la radioactivité. Entre autres, elle a étudié la radioactivité du polonium qui se dégrade selon la réaction de fission nucléaire suivante.
|^{218}_{84}\text{Po}\ \rightarrow\ ^{214}_{82}\text{Pb} \ +\ ^4_2\alpha|
Dans cette réaction, on peut observer les phénomènes suivants.
-
Une particule alpha est émise |(^4_2\alpha).|
-
Le nombre de masse |(A)| diminue de 218 à 214 puisque le polonium |(\text{Po})| a perdu 4 nucléons (2 protons et 2 neutrons qui se trouvent maintenant sous forme de particule |\alpha.|
-
Le numéro atomique |(Z)| diminue de 84 à 82, ce qui signifie que 2 protons sont perdus. L’atome de polonium |(\text{Po})| devient donc un atome de plomb |(\text{Pb}).| L’atome de plomb 214 est plus léger et plus stable que l’atome de polonium 218.
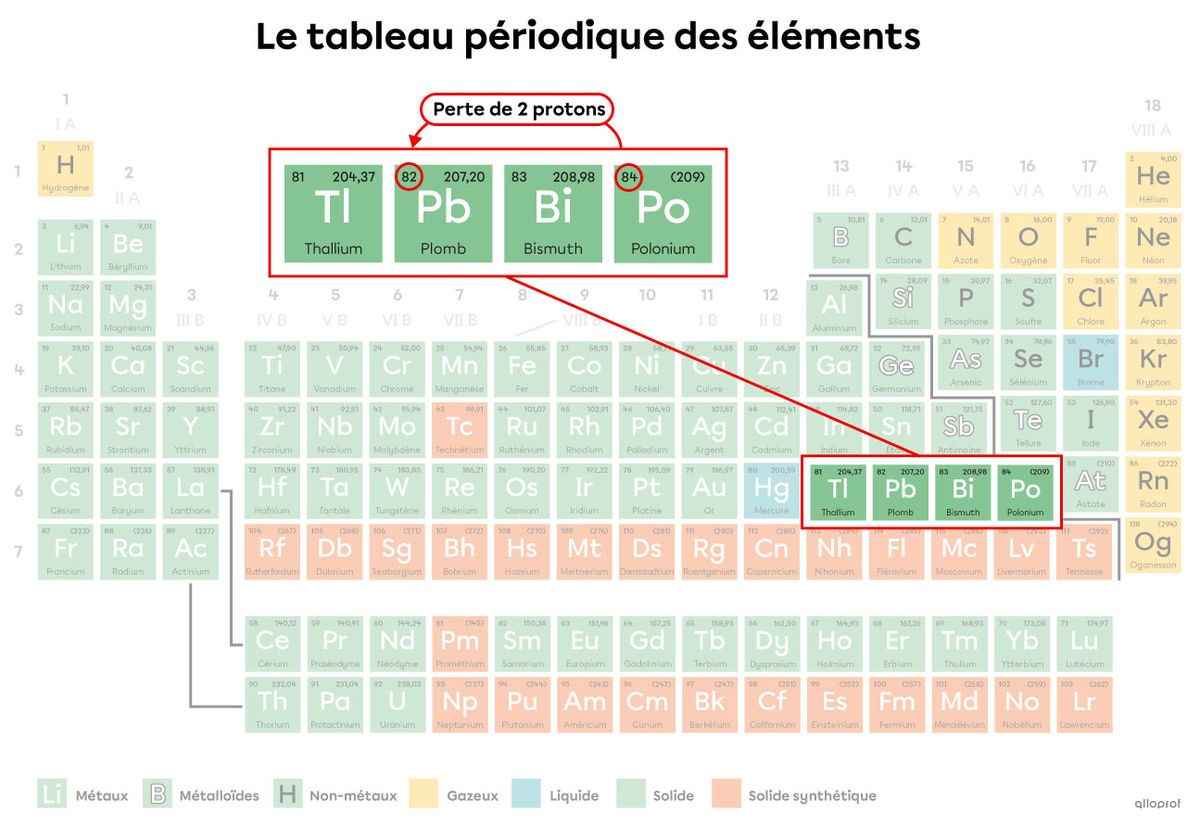
Le rayonnement bêta |(\beta),| aussi appelé particule bêta |(\beta),| est une particule très légère et hautement énergétique.
Une particule |\beta| peut avoir une charge positive ou une charge négative. Lorsqu’une particule |\beta| est positive, il s’agit d’un positon. Lorsqu’elle est négative, il s’agit d’un électron. Uniquement le cas des particules bêta négatives sera abordé.
En fonction du contexte, on peut représenter les particules |\beta| négatives de diverses manières.
| |\text{e}^-| | |\beta| | |\beta^-| | |^0_{-1}\beta| |
Les particules |\beta| négatives sont généralement émises lorsqu’un atome léger a trop de neutrons. Le noyau de cet atome se dégrade en transformant un neutron en proton, ce qui émet une particule |\beta.|
Selon le modèle élaboré au début du 20e siècle, on peut représenter cette transformation de la manière suivante en employant la notation A/Z.

Dans ce contexte, l’émission de rayonnements |\beta| engendre les modifications suivantes :
-
l’atome qui se désintègre perd 1 neutron et gagne 1 proton;
-
son numéro atomique |(Z)| augmente de 1;
-
son nombre de masse |(A)| reste le même;
-
en bref, l’atome produit lors de cette réaction nucléaire a sensiblement la même masse qu’auparavant, mais il est plus stable grâce à un ratio plus favorable entre le nombre de protons et de neutrons.
Le carbone 14 est un isotope radioactif du carbone qui se désintègre par rayonnement |\beta| selon l’équation suivante.
||^{14}_{6}\text{C}\ \rightarrow\ ^{14}_7\text{N}\ +\ ^0_{-1}\beta||
Lors de cette réaction, on peut observer les phénomènes suivants.
-
Une particule bêta est émise |(^0_{-1}\beta).|
-
Le nombre de masse |(A)| reste le même, soit 14. Autrement dit, la somme du nombre de neutrons et de protons reste la même.
-
Le numéro atomique |(Z)| passe de 6 à 7. Ainsi, le carbone 14 |(^{14}_{6}\text{C})| possède 6 protons et 8 neutrons. Il se transforme ensuite en azote 14 |(^{14}_{7}\text{N}),| qui lui, possède 7 protons et 7 neutrons. Au cours de la réaction, un neutron s’est donc transformé en proton.
-
En bref, l’atome de carbone |(\text{C})| devient un atome d’azote |(\text{N}).| Cet atome d’azote 14 a sensiblement la même masse que l’atome de carbone 14, mais a un proton de plus et un neutron de moins.

Dans l’exemple précédent, il est indiqué qu’un atome se dégradant par rayonnement |\beta| engendre un autre atome et une particule |\beta.| Cependant, dans les années 1920, plusieurs physiciens se rendent compte qu’une telle dégradation ne respecte pas la loi de la conservation de la masse : la masse de l’atome avant sa dégradation (|m_\text{initiale}|) n’est pas exactement la même que la masse du nouvel atome et d’une particule bêta (|m_\text{finale}).|
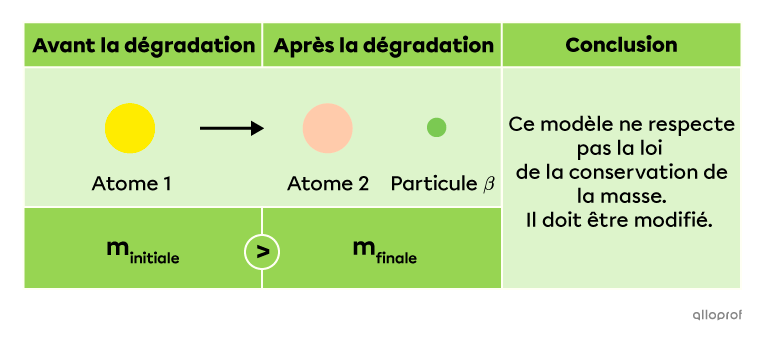
Face à cette étrange découverte, le physicien Wolfgang Pauli en déduit qu’une autre particule doit surement être émise lors de cette réaction. Cette particule est un neutrino |(\nu).| Il s’agit d’une particule subatomique élémentaire neutre et très légère. Ainsi, il serait plus précis de représenter la dégradation par rayonnement |\beta| de la manière suivante.
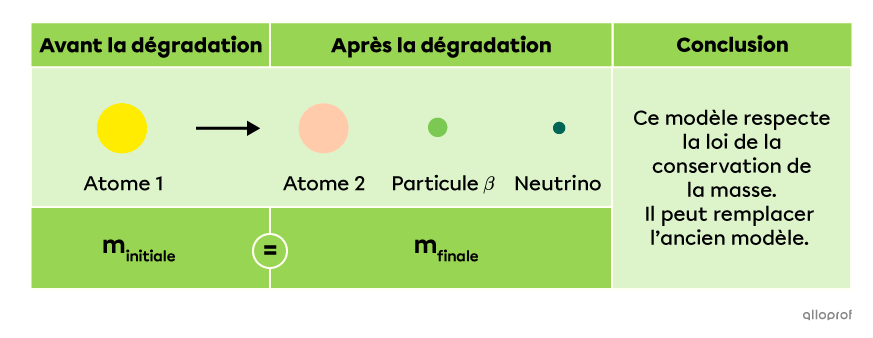
En employant la notation A/Z, on peut décrire cette réaction nucléaire ainsi.
|^{A}_Z\text{X}\ \rightarrow\ ^{A}_{Z+1}\text{X}\ +\ ^0_{-1}\beta\ +\ ^0_0\nu\ +\ \text{Énergie}|
Le rayonnement gamma |(\gamma)| est un rayonnement électromagnétique hautement énergétique qui n’a pas de masse.
On peut représenter le rayonnement |\gamma| de diverses manières.
| |\gamma| | |^0_0\gamma| |
L’émission de rayonnement |\gamma| accompagne souvent les réactions de dégradation par rayonnement |\alpha| ou |\beta.| Le rayonnement gamma peut aussi se produire lorsqu’un atome hautement énergétique perd son énergie. On dit alors que l’atome passe de l’état excité à l’état fondamental.
Dans ce contexte, on peut employer la notation A/Z et représenter cette émission d’énergie ainsi.

Un atome de cobalt hautement énergétique |^{60}_{27}\text{Co}^*| émet un rayonnement |\gamma| tel qu’indiqué dans cette équation :
|^{60}_{27}\text{Co}^*\ \rightarrow\ ^{60}_{27}\text{Co}\ +\ ^0_0\gamma|
Lors de cette réaction, on peut observer les phénomènes suivants.
-
Une grande quantité d’énergie est émise sous forme de rayonnement |\gamma.|
-
Le nombre de masse |(A = 60)| et le numéro atomique |(Z = 27)| du cobalt restent les mêmes.
-
En bref, le cobalt 60 ne subit aucune perte de neutrons, de protons ou d’électrons. Il émet simplement de l’énergie.
Institut de radioprotection et de sûreté nucléaire. (2021). La radioécologie marine.
https://www.irsn.fr/FR/connaissances/Environnement/radioactivite-environnement/radioecologie/Pages/5-radioecologie-marine.aspx#.X41akkE6-70
Institut de radioprotection et de sûreté nucléaire. (2021). Les sources de radioactivité naturelle.
https://www.irsn.fr/FR/connaissances/Environnement/radioactivite-environnement/sources-radioactivite/Pages/1-sources-radioactivite-naturelle.aspx