Malgré que les cônes soient des corps ronds, la façon de calculer leur volume est la même que celle des pyramides à la différence près que l’aire de la base sera toujours celle d’un disque.
Afin de déterminer l'espace en 3 dimensions qu'un cône occupe, on considère d'abord l'aire de sa base pour ensuite la multiplier par la mesure de sa hauteur. Il ne reste qu’à diviser par 3.
|V = \dfrac{A_b \times h}{3}| ou |V=\dfrac{\pi r^2\times h}{3}|
où
||\begin{align} V&: \text{Volume}\\A_b &: \text{Aire de la base}\\ h &: \text{hauteur du cône}\\ r &: \text{rayon de la base}\end{align}||
Dans un restaurant, on sert toutes les boissons dans des verres de même dimension.
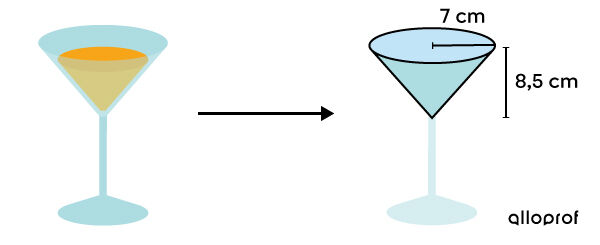
Afin de bien fixer le prix des différentes boissons, détermine, en |\text{cm}^3,| le volume maximum de liquide que peut contenir un verre.
-
Identifier le solide
Il s'agit d'un cône dont l'apex pointe vers le bas. -
Appliquer la formule ||\begin{align} V &= \dfrac{A_b \times h}{3}\\\\ &= \dfrac{\pi r^2 \times h}{3} \\\\&= \dfrac{\pi (7)^2 \times 8{,}5}{3}\\\\&\approx 436{,}16 \ \text{cm}^3\end{align}||
-
Interpréter la réponse
Chaque verre de ce format pourra contenir un maximum de |436{,}16\ \text{cm}^3| de liquide.
Dans certains problèmes, on peut rechercher la mesure de la base ou la hauteur du cône alors que le volume est donné. C’est ce qui s’appelle trouver une mesure manquante d'un cône à partir du volume.
Malgré toutes les formules qui sont disponibles, il arrive que certaines données soient manquantes. Dans ces cas, il faut utiliser d'autres concepts mathématiques afin d'obtenir le résultat recherché. Par exemple, la mesure de la hauteur ne sera pas toujours donnée. Ainsi, le théorème de Pythagore est souvent utilisé.
Trouver la mesure de la hauteur à partir de l’apothème
Dans le cas d'un cône droit, on peut obtenir un triangle rectangle en traçant le segment issu de l'apex et en rejoignant le cercle qui forme la base, la hauteur du cône et le rayon de la base.
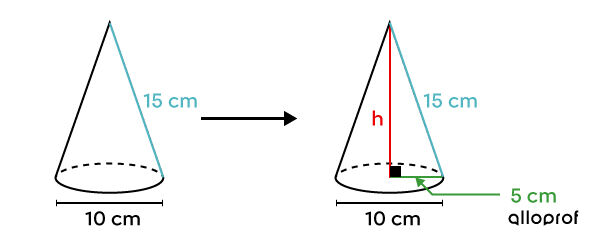
Puisque la hauteur intercepte le centre de la base et qu'il s'agit d'un cône droit, la mesure de la cathète horizontale correspond à la moitié de la mesure du diamètre.
En associant la mesure d'une cathète avec celle du rayon de la base, l'autre cathète avec celle de la hauteur du cône et l'apothème avec celle de l'hypoténuse, on peut utiliser la relation de Pythagore.
||\begin{align}\color{#3A9A38}{a}^2 + \color{#EC0000}{b}^2 &=\color{#51B6C2}{c}^2\\ \color{#3A9A38}{5}^2 +\color{#EC0000}{h}^2 &= \color{#51B6C2}{15}^2\\ \color{#EC0000}{h}^2 &= 200\\ \color{#EC0000}{h} &\approx 14{,}14 \ \text{cm}\end{align}||
Donc, la hauteur du cône est d’environ |14{,}14 \ \text{cm}.|
Si on cherche la mesure de l’apothème à partir de la hauteur, c’est encore le théorème de Pythagore qu’il faut utiliser.