-
A set is a group of elements that have a certain characteristic in common.
-
An element is an item that is part of a set.
There are many types of sets, which are classified depending on the number of elements they contain or on the characteristics of their elements.
An empty set is a set that contains no elements. It is represented by the symbol |\varnothing| or by 2 empty braces: |\{\ \}.|
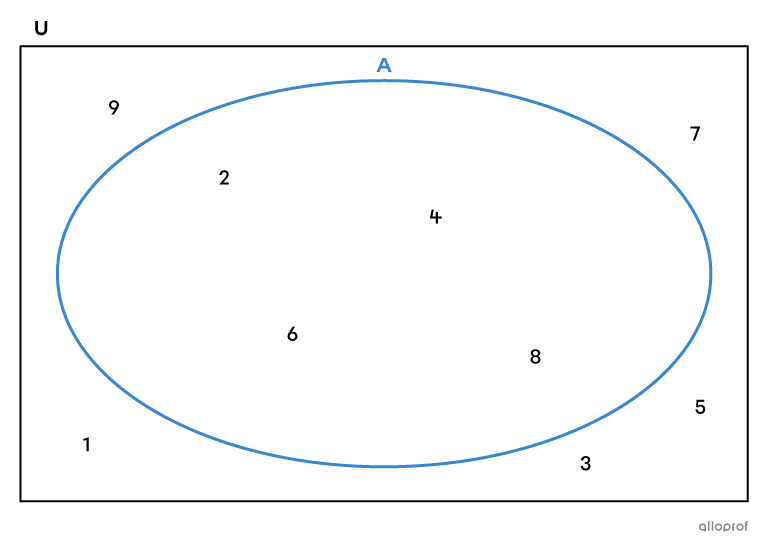
In this Venn diagram, the set |A| is an empty set, since it does not contain any elements.
||A = \varnothing||
-
A finite set is a set with a fixed number of elements. This number of elements is a natural number.
-
An infinite set is a set with an undetermined number of elements. This means that it contains an infinite number of elements.
Sometimes we refer to the cardinality of a set. This is the number of elements contained in the set.
The various number sets |(\mathbb N, \mathbb Z, \mathbb Q, \mathbb Q', \mathbb R)| are infinite sets.
A singleton or unit set is a set that contains only one element.
-
|A = \{2,4,6,8,10\}| is a finite set that contains |5| elements.
-
|B = \{1,2,3, \ldots ,100\}| is a finite set that contains |100| elements.
-
|C = \{\text{Prime numbers less than}\ 250\}| is a finite set.
-
|D = \{\text{Factors of}\ 27\}| is a finite set.
-
|E = \left\{\text{Fractions equivalent to}\ \dfrac{3}{4} \right\}| is an infinite set.
-
|F = \{\text{Multiples of}\ 5\}| is an infinite set.
-
|G = \{12\}| is a singleton or unit set, since it is a finite set that contains only one element.
A solution set is a set that consists of the different solutions to a given equation or inequality. It can contain 0 solutions or one or more solutions, depending on the problem.
-
The solution set of the equation |2x+5=25| is |A=\{10\}.|
-
The solution set of the equation |2a+3b=8| is |B=\{(4,0), (1,2), (-2,4), (-5,6), \ldots \}.|
-
The solution set of the inequality |4x< 12| is |C=\{x \in\mathbb R\ \vert\ x<3\},| which is all the |x|-values that belong to the universal set of real numbers and are strictly less than |3.|
For inequalities, there are several possible representations of a solution set: set builder notation, the use of a number line and interval notation.
A number set is a set in which all elements are a certain type of number. There are several of these:
-
Natural numbers |\mathbb N,| such as |2| and |657;|
-
Integers |\mathbb Z,| such as |2,| |-74,| and |-36;|
-
Rational numbers |\mathbb Q,| such as |2,| |-74,| |-\dfrac{5}{6}| and |2.\overline{3};|
-
Irrational numbers |\mathbb Q',| such as |\pi| and |\sqrt{2};|
-
Real numbers |\mathbb R,| a set which includes all the previous sets of numbers.

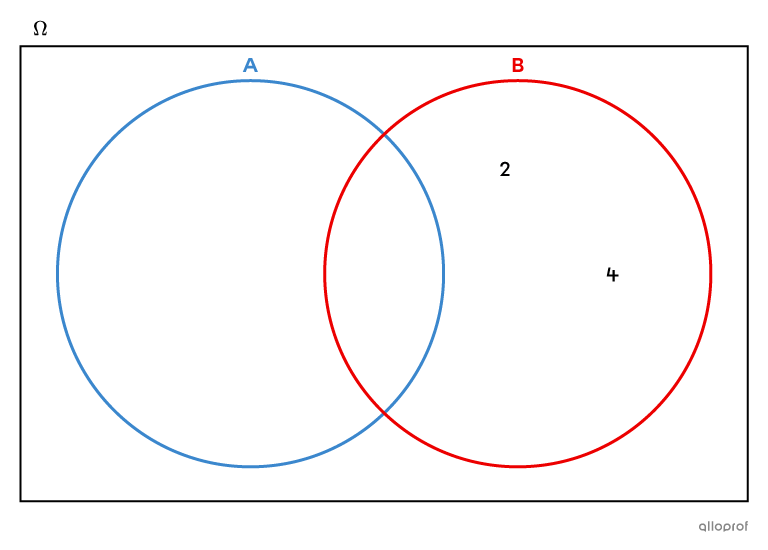
Disjoint sets are sets that have no elements in common.
The intersection of 2 disjoint sets is the empty set and can be written as |A\cap B=\varnothing.|
In this Venn diagram, set |A| contains odd numbers, while set |B| contains even numbers. These are 2 disjoint sets, since their intersection is empty.
-
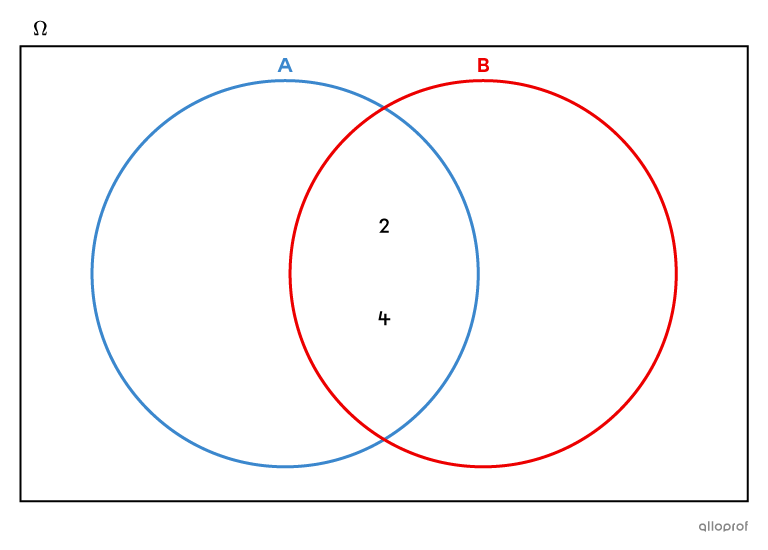
Equal sets are sets that contain exactly the same elements.
-
Distinct sets are sets that are not equal.
When we represent two equal sets in a Venn diagram, only the intersection is non-empty. Therefore, there is no element of one set that is not also part of the other set.
In this Venn diagram, the sets |A = \{2, 4\}| and |B = \{2, 4\}| are equal, since they contain exactly the same elements.
In the context of a theory or a problem, the universal set, or universe |(U),| represents the set of all the elements considered. It is the starting set from which other sets can be defined.
In the context of functions, the domain and codomain are universal sets. In probability, the sample space |(\Omega)| is a universal set.
The set |A = \{2, 4, 6, 8\}| consists of all the even numbers in the universal set |U = \{1, 2, 3, 4, 5, 6, 7, 8, 9\}.|