La masse atomique correspond à la masse d’un atome. Cette masse peut se mesurer en grammes |\text{(g)}| ou en unités de masse atomique |\text{(u)}.|
La masse atomique représente la masse de tous les neutrons et des protons constituant son noyau. La masse des électrons n’est pas prise en compte, car les électrons sont environ 2 000 fois plus légers que les protons et les neutrons. Leur masse a donc très peu d’influence sur la masse totale de l’atome.
| Masse d'un neutron |\text{(g)}| |
Masse d'un proton |\text{(g)}| |
Masse d'un électron |\text{(g)}| |
|---|---|---|
| |1{,}675 \times 10^{-24}| | |1{,}673 \times 10^{-24}| | |9{,}109 \times 10^{-28}| |
La masse atomique peut se mesurer en grammes |\text{(g)},| mais les valeurs de masse obtenues sont très petites. On privilégie donc l’unité de masse atomique |\text{(u)}| afin de faciliter les calculs.
|1\ \text{u}=1{,}66\times10^{-24}\ \text{g}|
Par convention, cette valeur correspond au douzième de la masse atomique du carbone |(1\ \text{u}= \dfrac{1}{12} \times m_c)|. Puisque l’unité de masse atomique est déterminée relativement à la masse d’un atome de carbone, on appelle ce type de masse atomique la masse atomique relative.
Un atome de potassium 39 |(^{39} \text{K})| a une masse atomique relative de |39{,}0\ \text{u}|. Quelle est sa masse atomique en grammes?
À partir du facteur de conversion et des données présentes dans l’énoncé, on sait que :
|\begin{align}1\ \text{u} &= 1{,}66 \times 10^{-24}\ \text{g}\\39{,}0\ \text{u}&= ?\end{align}|
Par produit croisé, on obtient :
|\begin{align}m_{\text{K}}&=\dfrac{(39{,}0\ \text{u}) \times (1{,}66 \times 10^{-24}\ \text{g})}{1\ \text{u}} \\m_{\text{K}}&\approx 6{,}47 \times 10^{-23}\ \text{g}\end{align}|
Ainsi, la masse atomique d’un atome de potassium 39 |(^{39} \text{K})| est d’environ |6{,}47 \times 10^{-23}\ \text{g}.|
Un atome d’azote a une masse atomique de |2{,}32 \times 10^{-23}\ \text{g}.| Quelle est sa masse atomique relative en unités de masse atomique |\text{u}|?
À partir du facteur de conversion et des données présentes dans l’énoncé, on sait que :
|\begin{align}1\ \text{u} &= 1{,}66 \times 10^{-24}\ \text{g}\\?&= 2{,}32 \times 10 ^{-23}\ \text{g}\end{align}|
Par produit croisé, on obtient :
|\begin{align}m_{\text{N}}&=\dfrac{(1\ \text{u}) \times (2{,}32 \times 10^{-23}\ \text{g})}{1{,}66 \times 10^{-24}\ \text{g}} \\m_{\text{N}}&\approx 14{,}0\ \text{u}\end{align}|
Ainsi, la masse atomique relative de cet atome d’azote est d’environ |14{,}0\ \text{u}.|
Afin de s’exprimer avec précision, on parle de masse atomique lorsque la masse de l’atome est en grammes |\text{(g)}.| Cependant, on parle de masse atomique relative quand on fait référence à une valeur exprimée en unités de masse atomique |\text{(u)}.|
Les éléments peuvent être caractérisés par leur numéro atomique |\text{(Z)},| mais aussi par leur nombre de masse.
Le nombre de masse (|\text{A}|) correspond à la somme du nombre de neutrons et de protons qui constituent le noyau d’un atome.
Un atome d’azote 14 |(^{14}\text{N})| est composé de 7 protons, 7 neutrons et 7 électrons.
-
Son numéro atomique |\text{(Z)}| est 7 puisqu’il possède 7 protons.
-
Son nombre de masse |\text{(A)}| est 14 puisqu’il possède 7 protons et 7 neutrons |(\text{A}=7+7=14).| C’est d’ailleurs la raison pour laquelle il se nomme « azote 14 » |(^{14}\text{N}).|
Dans la nature, les éléments existent sous différentes formes. En effet, plusieurs atomes peuvent avoir le même numéro atomique, mais un nombre de neutrons différent. Ces atomes sont des isotopes.
Les isotopes sont des atomes qui ont le même numéro atomique, mais pas le même nombre de masse. Ainsi, les isotopes ont le même nombre de protons, mais pas le même nombre de neutrons. Cela implique également que les isotopes n’ont pas la même masse atomique relative.
On peut facilement distinguer les isotopes grâce à la notation A/Z.
Le potassium 39 et le potassium 40 sont des isotopes. Leur nombre de masse est différent. La notation A/Z de ces isotopes est la suivante.
|_{19}^{39}\text{K}| et |_{19}^{40}\text{K}|
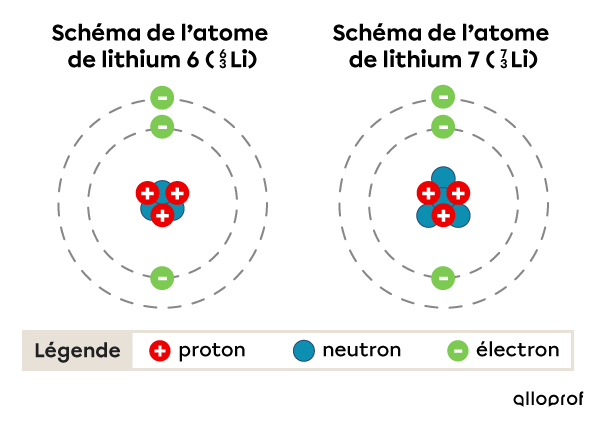
Voici le modèle atomique simplifié de deux atomes de lithium. Ces deux atomes n’ont pas le même nombre de neutrons (soit 3, soit 4 neutrons), mais ils ont le même nombre de protons (3). Ce sont donc des isotopes.
Le noyau du second isotope comprend plus de particules que le premier. Il a donc une plus grande masse atomique que le premier.
Le carbone a plusieurs isotopes. Les plus communs sont le carbone 12, le carbone 13 et le carbone 14. Voici quelques caractéristiques de ces 3 isotopes.
| Isotope | Carbone 12 | Carbone 13 | Carbone 14 |
|---|---|---|---|
| Nombre de masse |\text{(A)}| | |12| | |13| | |14| |
| Numéro atomique (|\text{Z}|, nombre de protons) | |6| | |6| | |6| |
| Nombre de neutrons | |6| | |7| |
|8| |
On note les points suivants :
-
Puisqu’il s’agit d’isotopes du même élément (le carbone), ces 3 isotopes ont le même numéro atomique |\text{(Z)}|, et donc le même nombre de protons, soit 6 protons.
-
Par contre, ils n’ont pas le même nombre de neutrons |\text{(N)}|. C’est la raison pour laquelle leur nombre de masse |\text{(A)}| varie.
Un isotope radioactif est un isotope dont le noyau est instable. Cette instabilité fait en sorte que le noyau de l’isotope se dégrade et émet de l’énergie.
Les isotopes d’un même élément n’ont pas tous la même stabilité. Souvent, l’instabilité du noyau des isotopes radioactifs est due à un excès de protons et/ou de neutrons.
Les isotopes radioactifs sont naturellement présents dans l’environnement, mais ils peuvent aussi être générés artificiellement. On peut exploiter leur radioactivité afin de créer des traitements contre certains types de cancer, de fabriquer des détecteurs de fumée, de générer de l’énergie électrique, etc.
Dans la nature, il existe plusieurs isotopes du carbone. Le carbone 12 et le carbone 13 sont les plus stables de ces isotopes. D’autres isotopes du carbone, comme le carbone 14, sont instables. Avec le temps, ce dernier se dégrade et sa concentration diminue. Cette caractéristique permet aux archéologues de dater certains restes (ossements, coquillages, etc.) ou objets anciens (objets en bois, etc.).
Dans la nature, il existe plusieurs isotopes d’un même élément. Chacun d’entre eux a une masse atomique différente. Certains isotopes sont présents en grande quantité, comme le carbone 12, tandis que d’autres, plus instables, sont présents en petite quantité, comme le carbone 14. On peut donc faire une moyenne des masses atomiques de tous les isotopes d’un élément en fonction de leur abondance dans la nature.
La masse atomique moyenne correspond à une moyenne pondérée de la masse atomique relative des isotopes d’un même élément. Cette moyenne pondérée se calcule en fonction de l’abondance naturelle des isotopes.
On peut trouver la masse atomique moyenne d’un élément dans le tableau périodique. Celle-ci se mesure en unités de masse atomique |\text{(u)}.| La masse atomique moyenne est donc aussi une masse atomique relative.

Dans le tableau périodique, la masse atomique moyenne du béryllium est de |9{,}01\ \text{u}.| Il est à noter que tous les tableaux périodiques n’ont pas nécessairement le même format. La valeur de la masse atomique moyenne peut se trouver dans différentes zones de la case de l’élément. Il faut donc se référer à la légende du tableau utilisé.
On peut également utiliser la formule suivante pour calculer la masse atomique moyenne.
||\overline{m} = (\%_{isotope\ 1} \times m_{isotope\ 1}) + (\%_{isotope\ 2} \times m_{isotope\ 2})+...||
où
|\overline{m}| représente la masse atomique moyenne d’un élément
|\%_{isotope\ 1}| représente l’abondance naturelle de l’isotope 1
|m_{isotope\ 1}| représente la masse atomique relative de l’isotope 1
|\%_{isotope\ 2}| représente l’abondance naturelle de l’isotope 2
|m_{isotope\ 2}| représente la masse atomique relative de l’isotope 2
En considérant les valeurs qui se trouvent dans le tableau suivant, quelle est la masse atomique moyenne du rubidium |\text(Rb)|?
| Isotope | Rubidium 85 | Rubidium 87 |
|---|---|---|
| Abondance naturelle de l'isotope | |72{,}2\ \%| | |27{,}8\ \%| |
| Masse atomique relative de l'isotope | |84{,}9\ \text{u}| | |86{,}9\ \text{u}| |
Afin de déterminer la masse atomique moyenne du rubidium, on applique la formule précédente.
||\overline{m} = (\%_{isotope\ 1} \times m_{isotope\ 1}) + (\%_{isotope\ 2} \times m_{isotope\ 2})+...||
On remplace les valeurs à partir des données du tableau.
\begin{align}\overline{m}_{\text{Rb}}&=(72{,}2\ \% \times84{,}9\ \text{u}) + (27{,}9\ \% \times 86{,}9\ \text{u})\\ \overline{m}_{\text{Rb}}&\approx 85{,}5\ \text{u}\end{align}
Ainsi, la masse atomique moyenne du rubidium est d’environ |85{,}5\ \text{u}.| Cette valeur calculée est cohérente avec celle qui se trouve dans le tableau périodique.

Les 2 isotopes stables du bore se présentent dans les proportions suivantes : |19{,}78\ \%| de bore |10| (|^{10}\text{B}|) et |80{,}22\ \%| de bore |11| |(^{11}\text{B)}|. Quelle est la masse atomique moyenne du bore?
Les masses atomiques relatives des isotopes du bore ne sont pas indiquées explicitement. Cependant, on peut estimer que le bore |10| a une masse atomique de |10\ \text{u}| et que le bore |11| a une masse atomique de |11\ \text{u}.|
Afin de déterminer la masse atomique moyenne du bore, on applique la formule suivante.
||\overline{m} = (\%_{isotope\ 1} \times m_{isotope\ 1}) + (\%_{isotope\ 2} \times m_{isotope\ 2})+...||
On remplace les valeurs à partir des données dont on dispose.
|\begin{align}\overline{m}_{\text{B}}&=(19{,}78\ \% \times10\ \text{u}) + (80{,}22\ \% \times 11\ \text{u})\\ \overline{m}_{\text{B}}&\approx 10{,}8\ \text{u}\end{align}|
Ainsi, la masse atomique moyenne du bore est d’environ |10{,}8\ \text{u}.| Cette valeur calculée est cohérente avec celle qui se trouve dans le tableau périodique.