Cette MiniRécup porte sur les situations de proportionnalité, les situations inversement proportionnelles et les suites arithmétiques. Ses vidéos interactives, son résumé et son exercice récapitulatif te permettront de faire une bonne révision sur ces sujets.
Dans cette MiniRécup, il est question notamment des situations de proportionnalité. Il est donc important que tu saches ce qu’est une proportion. Dans une proportion, on retrouve des rapports et des taux. Ce sont toutes des notions que tu dois maitriser.
De plus, comme on trace le graphique associé à différentes mises en situation, tu dois avoir une bonne compréhension du plan cartésien. Tu dois être capable d’y situer des points à partir d’une table de valeurs.
Finalement, comme on discute de la règle de ces 3 types de situations, il est préférable que tu maitrises les bases de l’algèbre. Par exemple, tu dois être capable de calculer la valeur d’une expression algébrique et d’isoler une variable pour résoudre une équation.
Voici le tableau des synonymes qui a été présenté dans la dernière vidéo.
| Les suites (Secondaire 1) |
Les types de situations (Secondaire 2) |
Les fonctions (Secondaire 3) |
|
|---|---|---|---|
 |
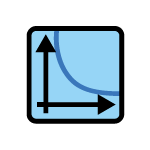
Situation de proportionnalité | Fonction linéaire ⇒ Variation directe ⇒ |y=ax| |
|
 |
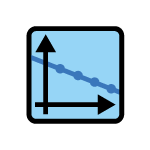
Situation inversement proportionnelle | Fonction rationnelle ⇒ Variation inverse ⇒ |y=\dfrac{k}{x}| |
|
 |
Suite arithmétique ⇒ Terme = Régularité × Rang + Terme de rang |0|
|
Fonction affine ⇒ Variation indirecte ⇒ |y=ax+b| |
|
| ||a|| | Régularité ⇒ Bond ⇒ Raison |
Coefficient de proportionnalité | Taux de variation ⇒ Paramètre |a| |
| ||b|| | Valeur initiale ⇒ Terme de rang |0| ⇒ Ajustement ⇒ Terme constant |
Ordonnée à l’origine ⇒ Paramètre |b| |
Situation de proportionnalité
Une situation de proportionnalité, aussi appelée situation de variation directe ou fonction linéaire, présente les caractéristiques suivantes :
-
Dans la description verbale, il est question d’un taux constant.
-
Le graphique est une droite qui passe par l’origine du plan cartésien.
-
La règle est de la forme suivante : |y=ax.|
-
Les valeurs des 2 variables dans la table de valeurs varient dans le même sens.
On peut résoudre une situation de proportionnalité à l’aide de l’une ou l’autre des stratégies suivantes :
-
le coefficient de proportionnalité;
-
le facteur de changement;
-
le procédé additif;
-
le produit croisé;
-
la règle.
Situation inversement proportionnelle
Une situation inversement proportionnelle, aussi appelée situation de variation inverse ou fonction rationnelle, présente les caractéristiques suivantes :
-
Dans la description verbale, il est question d’une division en parts égales.
-
Le graphique est une courbe qui se rapproche des 2 axes sans y toucher.
-
La règle est de la forme suivante : |y=\dfrac{k}{x}.|
-
Les valeurs des 2 variables dans la table de valeurs varient dans le sens contraire.
On peut résoudre une situation inversement proportionnelle à l’aide de l’une ou l’autre des stratégies suivantes :
-
le facteur de changement inverse;
-
le produit constant;
-
la règle.
Suite arithmétique
Une suite arithmétique, qu’on peut associer aux fonctions affines, présente les caractéristiques suivantes :
-
Dans la description verbale, il est question d’une variation constante (la régularité).
-
Le graphique est une droite qui ne passe pas nécessairement par |(0,0).|
-
La règle est de la forme suivante : |y=ax+b.|
-
Dans la table de valeurs, on peut calculer un taux de variation constant.
On peut trouver une valeur manquante dans une suite à l’aide de l’une ou l’autre des stratégies suivantes :
-
Faire des bonds réguliers jusqu’à arriver au rang voulu.
-
Utiliser la règle.