To calculate the perimeter of a regular polygon, we need to know the measure of the side and the number of sides. To calculate the area, we also need to know the measure of the apothem.
Every regular polygon is named according to its number of sides.

Just like for the perimeter of a plane figure, the perimeter of a regular polygon is calculated by adding up the measures of all its sides. Since all the sides of a regular polygon have the same measurement, we can generalize the calculation of its perimeter as follows:
||\begin{align}P&=\overbrace{s+s+\ldots+s}^{\large\text{$n$ times}}\\&=n\times s\end{align}||where
|P:| perimeter of the regular polygon
|n:| number of sides
|s:| measure of one side
By moving the cursor in the following interactive animation, it is possible to see how to calculate the perimeter of a regular polygon.
What is the perimeter of a regular nonagon whose side measures |5.2\ \text{cm}|?
A regular nonagon is a |9|-sided polygon. Its perimeter can be calculated as follows:||\begin{align}P&=n\times s\\&=9\times5.2\\&=46.8\ \text{cm}\end{align}||Answer: The perimeter of the regular nonagon is |46.8\ \text{cm}.|
Sometimes the Pythagorean Theorem is needed to calculate the perimeter of a regular polygon.
What is the perimeter of this regular heptagon?

The measure of the apothem |(a)| and the measure of the radius of the circle that circumscribes the polygon, or the segment connecting the centre to a vertex |(r)|, are given.
In a regular polygon, these 2 segments form a right triangle with half of one side |\left(\dfrac{s}{2}\right)\!.| Therefore, we can use the Pythagorean theorem.||\boldsymbol{\color{#fa7921}{a}}^2+\left(\boldsymbol{\color{#3b87cd}{\dfrac{s}{2}}}\right)^{\!2}=\boldsymbol{\color{#7cca51}{r}}^2||
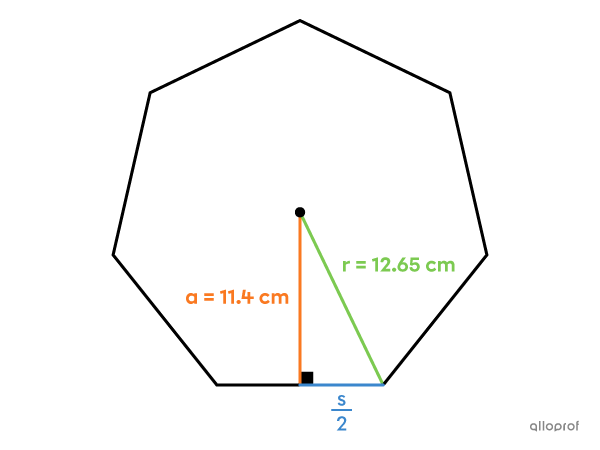
By substituting the values in the equation, then isolating |s,| the measure of one side of the regular heptagon can be found.||\begin{align}\boldsymbol{\color{#fa7921}{11.4}}^2+\left(\dfrac{s}{2}\right)^{\!2}&=\boldsymbol{\color{#7cca51}{12.65}}^2\\[3pt]129.96+\left(\dfrac{s}{2}\right)^{\!2}&=160.0225\\[3pt]129.96\boldsymbol{\color{#ec0000}{-129.96}}+\left(\dfrac{s}{2}\right)^{\!2}&=160.0225\boldsymbol{\color{#ec0000}{-129.96}}\\[3pt]\left(\dfrac{s}{2}\right)^{\!2}&=30.0625\\[3pt]\color{#ec0000}{\sqrt{\color{black}{\left(\dfrac{s}{2}\right)^{\!2}}}}&=\color{#ec0000}{\sqrt{\color{black}{30.0625}}}\\[3pt]\dfrac{s}{2}&=\sqrt{30.0625}\\[3pt]\dfrac{s}{2}\boldsymbol{\color{#ec0000}{\times2}}&=\sqrt{30.0625}\boldsymbol{\color{#ec0000}{\times2}}\\[3pt]\boldsymbol{\color{#3b87cd}{s}}&\approx\boldsymbol{\color{#3b87cd}{10.97}}\ \text{cm}\end{align}||The perimeter can now be calculated.||\begin{align}P&=\boldsymbol{n}\times\boldsymbol{\color{#3b87cd}{s}}\\&=\boldsymbol{7}\times\boldsymbol{\color{#3b87cd}{10.97}}\\&=76.79\ \text{cm}\end{align}||Answer: The perimeter of the regular heptagon is approximately |76.79\ \text{cm}.|
Some conjectures can be made by comparing the perimeters of equivalent regular polygons.
The area of a regular polygon is often calculated by using one of the following 2 formulas:
||A=\dfrac{s\times a\times n}{2}||
||A=\dfrac{P\times a}{2}||
where
|A:| area of the regular polygon
|s:| measure of one side
|a:| apothem
|n:| number of sides
|P:| perimeter
These 2 equations are equivalent. In fact, to switch from one to the other, simply use the formula for the perimeter of a regular polygon.||\begin{align}A&=\dfrac{s\times a\times n}{2}\\[3pt]&=\dfrac{\boldsymbol{n\times s}\times a}{2}\\[3pt]&=\dfrac{\boldsymbol{P}\times a}{2}\\[3pt]\end{align}||
Both formulas are derived from a different geometric proof. The area of a regular polygon can be calculated using one of the following 2 methods:
By moving the cursor in the following interactive animation, it is possible to see how the area of a regular polygon can be calculated using the Sum of the Area of Triangles method.
A regular polygon with |n| sides can be decomposed into |\boldsymbol{n}| isometric isosceles triangles. In other words, to calculate the area of a regular polygon, simply multiply the area of one of the triangles by the number of triangles in the polygon.||\begin{alignat}{13}A_\text{regular polygon}&=\qquad\!A_\text{triangle}&&\times\begin{gathered}\text{Number of}\\\text{triangles}\end{gathered}\\[3pt]&=\;\dfrac{\color{#3b87cd}{\textbf{Base}}\times\color{#fa7921}{\textbf{Height}}}{2}&&\times\begin{gathered}\text{Number of}\\\text{triangles}\end{gathered}\end{alignat}||The following equivalences exist:
-
The base of the triangle corresponds to the measure of one side of the regular polygon |(\boldsymbol{\color{#3b87cd}{s}}).|
-
The height of the triangle corresponds to the apothem of the regular polygon |(\boldsymbol{\color{#fa7921}{a}}).|
-
The number of triangles corresponds to the number of sides of the regular polygon |(\boldsymbol{n}).|
Replacing the terms in the previous equation with the corresponding variables gives the following formula:||\begin{align}A&=\dfrac{s\times a}{2}\times n\\[3pt]&=\dfrac{s\times a\times n}{2}\end{align}||
What is the area of this regular polygon?
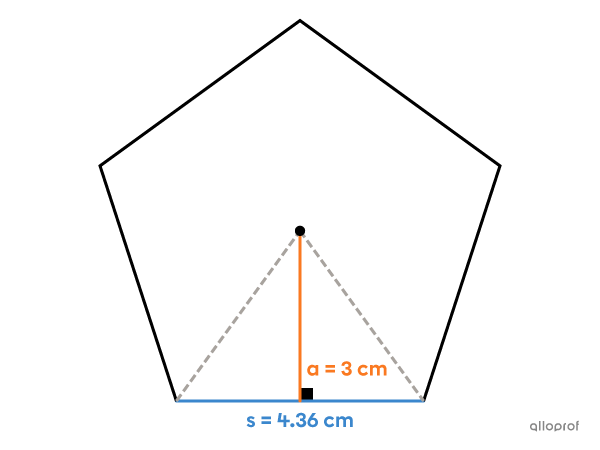
This is a regular pentagon, meaning a polygon with |5| sides |(n=5).| It is known that one side measures |(s=4.36\ \text{cm})| and that the apothem measures |(a=3\ \text{cm}).| The area of this regular pentagon can therefore be calculated as follows:||\begin{align}A&=\dfrac{\boldsymbol{\color{#3b87cd}{s}}\times\boldsymbol{\color{#fa7921}{a}}\times\boldsymbol{n}}{2}\\[3pt]&=\dfrac{\boldsymbol{\color{#3b87cd}{4.36}}\times\boldsymbol{\color{#fa7921}{3}}\times\boldsymbol{5}}{2}\\[3pt]&=32.7\ \text{cm}^2\end{align}||Answer: The area of this regular pentagon is |32.7\ \text{cm}^2.|
By moving the cursor in the following interactive animation, you can see how the area of a regular polygon can be calculated using the Area of a Parallelogram method.
A regular polygon can be split into triangles and then doubled to form a parallelogram. In other words, to calculate the area of a regular polygon, simply divide the area of the parallelogram by |2.|||\begin{alignat}{13}A_\text{regular polygon}&=\dfrac{A_\text{parallelogram}}{2}\\[3pt]&=\;\dfrac{\text{Base}\times\text{Height}}{2}\\[3pt]\end{alignat}||In a regular polygon, the following equivalences exist:
-
The base of the parallelogram corresponds to the measure of the perimeter |(\boldsymbol{\color{#3b87cd}{P}}).|
-
The height of the parallelogram corresponds to the apothem |(\boldsymbol{\color{#fa7921}{a}}).|
Replacing the terms in the previous equation with the corresponding variables gives the following formula:||A=\dfrac{P\times a}{2}||
What is the area of this regular polygon?
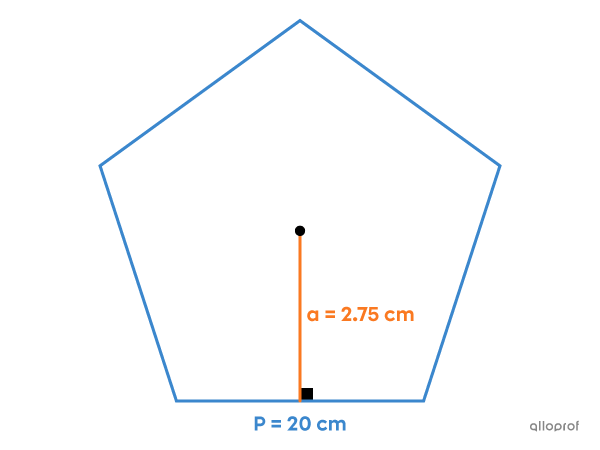
This is a regular pentagon, meaning a polygon with |5| sides. The perimeter is known |(P=20\ \text{cm}),| as is the measure of the apothem |(a=2.75\ \text{cm}).| The area of this regular pentagon can be calculated as follows:||\begin{align}A&=\dfrac{\boldsymbol{\color{#3b87cd}{P}}\times\boldsymbol{\color{#fa7921}{a}}}{2}\\[3pt]&=\dfrac{\boldsymbol{\color{#3b87cd}{20}}\times\boldsymbol{\color{#fa7921}{2.75}}}{2}\\[3pt]&=27.5\ \text{cm}^2\end{align}||Answer: The area of this regular pentagon is |27.5\ \text{cm}^2.|
Sometimes the Pythagorean Theorem is needed to calculate the area of a regular polygon.
What is the area of this regular dodecagon?

The measures of the perimeter |(P)| and the radius of the circle that circumscribes the polygon, or the segment connecting the centre to a vertex |(r),| are known.
In a regular polygon, the radius and apothem form a right triangle with half of one side |\left(\dfrac{s}{2}\right)\!.| Start by finding the measure of one side.||\begin{align}\boldsymbol{\color{#3b87cd}{P}}&=\boldsymbol{n}\times s\\[3pt]\boldsymbol{\color{#3b87cd}{136.04}}&=\boldsymbol{12}\times s\\[3pt]\color{#ec0000}{\dfrac{\color{black}{136.04}}{\boldsymbol{12}}}&=\color{#ec0000}{\dfrac{\color{black}{12\times s}}{\boldsymbol{12}}}\\[3pt]11.34\ \text{dm}&\approx s\end{align}||Next, apply the Pythagorean theorem.||\boldsymbol{\color{#fa7921}{a}}^2+\left(\dfrac{\boldsymbol{\color{#3b87cd}{s}}}{2}\right)^{\!2}=\boldsymbol{\color{#7cca51}{r}}^2||
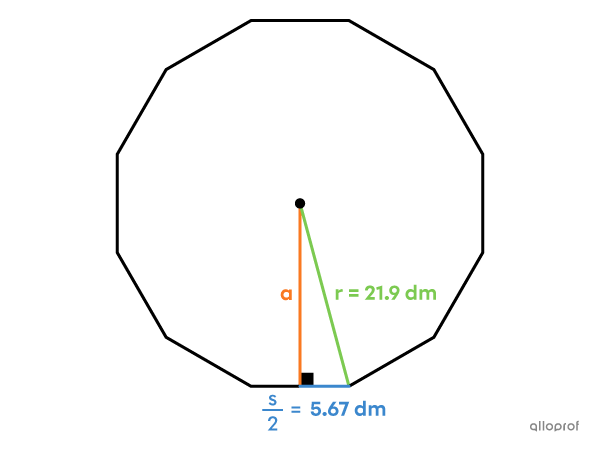
Substituting the values into the equation, then isolating |a,| gives the measure of the apothem of the regular dodecagon.||\begin{align}a^2+\left(\dfrac{\boldsymbol{\color{#3b87cd}{11.34}}}{2}\right)^{\!2}&=\boldsymbol{\color{#7cca51}{21.9}}^2\\[3pt]a^2+32.1489&=479.61\\[3pt]a^2+32.1489\boldsymbol{\color{#ec0000}{-32.1489}}&=479.61\boldsymbol{\color{#ec0000}{-32.1489}}\\[3pt]a^2&=447.4611\\[3pt]\color{#ec0000}{\sqrt{\color{black}{a^2}}}&=\color{#ec0000}{\sqrt{\color{black}{447.4611}}}\\[3pt]\boldsymbol{\color{#fa7921}{a}}&\approx\boldsymbol{\color{#fa7921}{21.15}}\ \text{dm}\end{align}||The area can now be calculated.||\begin{align}A&=\dfrac{\boldsymbol{\color{#3b87cd}{P}}\times\boldsymbol{\color{#fa7921}{a}}}{2}\\[3pt]&=\dfrac{\boldsymbol{\color{#3b87cd}{136.04}}\times\boldsymbol{\color{#fa7921}{21.15}}}{2}\\[3pt]&=1438.623\ \text{dm}^2\end{align}||Answer: The area of the regular dodecagon is |1438.623\ \text{dm}^2.|
To confirm you understand the area and perimeter of plane figures, see the following interactive CrashLesson:
