-
A trigonometric equation or inequality contains a trigonometric ratio, where the unknown |(x)| is found in the argument.
-
A 2nd-degree trigonometric equation or inequality contains at least one squared trigonometric ratio or at least one product of 2 trigonometric ratios.
Since trigonometric functions are periodic functions, these types of equations may have no solution, one solution, several solutions, or an infinite number of solutions.
Also, we need to use angles in radians.
Sometimes, the trigonometric equations to be solved contain only one trigonometric ratio. Other times, they contain more than one ratio. The strategies for solving those that have more than one ratio vary.
Here are some strategies you can use when solving an equation or inequality involving more than one trigonometric ratio.
-
Use the definitions of the trigonometric ratios.
-
Use the trigonometric identities.
-
Rewrite the fractions using a common denominator.
-
Set the restrictions.
-
Perform a change of variables.
-
Use factoring or the quadratic formula.
-
Use the unit circle or the inverse functions |\arcsin,| |\arccos| and |\arctan| to determine the solutions.
-
Calculate the period in order to give all of the solutions.
Note: The first 3 strategies allow you to rewrite the whole equation only in terms of either sine or cosine, making the equation easier to solve. However, most of the time, you do not need to use all of these strategies, nor do you necessarily need to use them in this particular order.
Here's a reminder of the definitions and trigonometric identities often used to solve trigonometric equations.
Definitions
||\begin{align}\tan(x)&=\dfrac{\sin(x)}{\cos(x)}\\[3pt]\text{cosec}(x)&=\dfrac{1}{\sin(x)}\\[3pt]\sec(x)&=\dfrac{1}{\cos(x)}\\[3pt]\cot(x)&=\dfrac{1}{\tan(x)}=\dfrac{\cos(x)}{\sin(x)}\end{align}||
Basic identities
||\begin{align}\cos(-x)&=\cos(x)\\[3pt] \sin(-x)&=-\sin(x) \end{align}||
Pythagorean identities
||\begin{alignat}{13}&\cos^2(x)&&+\sin^2(x)&&=1\\[3pt]&\quad\,1&&+\tan^2(x)&&=\sec^2(x)\\[3pt] &\cot^2(x)&&+\quad1&&=\text{cosec}^2(x)\end{alignat}||
The Trigonometric Identities of a Sum or a Difference
||\begin{align}\sin(A+B)&=\sin(A)\cos(B)+\cos(A)\sin(B)\\[2pt] \sin(A-B)&=\sin(A)\cos(B)-\cos(A)\sin(B)\\[2pt] \sin(2A)&=2\sin(A) \cos(A) \end{align}||
||\begin{align}\cos(A+B)&=\cos(A)\cos(B)-\sin(A)\sin(B)\\[2pt] \cos(A-B)&=\cos(A)\cos(B)+\sin(A)\sin(B)\\[2pt] \cos(2A)&=\cos^2(A)-\sin^2 (A)\end{align}||
||\begin{align}\tan(A+B)&=\dfrac{\tan(A)+\tan(B)}{1-\tan(A)\tan(B)}\\[5pt]\tan(A-B)&=\dfrac{\tan(A)-\tan(B)}{1+\tan(A)\tan(B)} \\[5pt] \tan(2A) &=\dfrac{2 \tan(A)}{1-\tan^2(A)} \end{align}||
When you use the inverse functions |\arcsin,| |\arccos| or |\arctan| on a calculator, you only get one angle value |(\theta).|
|\boldsymbol\arcsin|
We find the other angle that has the same sine value as |\theta| by calculating |\pi - \theta.|
|\boldsymbol\arccos|
We find the other angle that has the same cosine value as |\theta| by calculating |- \theta.|
|\boldsymbol\arctan|
For the function |\arctan,| we don't need to find the other angle, since the period of a tangent function is |\pi| and not |2\pi.|
Given that |\cos(x) = \dfrac{2}{3}| and that |x| is an angle between |0| and |\dfrac{\pi}{2},| what is the value of the following expressions?
a) |\sec(x)|
b) |\sin(x)|
c) |\cot(x)|
d) |\tan(-x)|
To answer these 4 sub-questions, we may be inclined to start by solving the equation |\cos(x)= \dfrac{2}{3}| to find the value of |x,| and then replace this value in each expression. However, this is not necessary.
a) We know that |\sec(x)| is the inverse of |\cos(x).| ||\sec(x)= \dfrac{1}{\cos(x)}||
To find the value of |\sec(x),| simply replace |\cos(x)| by |\dfrac{2}{3}.|
||\begin{align}\sec(x)&= \dfrac{1}{\cos(x)}\\ &= \dfrac{1}{\frac{\large2}{\large3}}\\ &= \dfrac{3}{2}\end{align}||
b) To find the value of |\sin(x)| from |\cos(x),| we can use the 1st Pythagorean identity: |\cos^2(x)+ \sin^2(x)=1.| We replace |\cos(x)| by its value, i.e., |\dfrac{2}{3},| then we isolate |\sin(x).|
||\begin{align}\cos^2(x)+ \sin^2(x)&=1\\ \left(\dfrac{2}{3}\right)^{\!2}+\sin^2(x)&=1\\ \dfrac{4}{9}+\sin^2(x)&=1\\ \sin^2(x)&=\dfrac{5}{9}\\ \sin(x)&=\sqrt{\dfrac{5}{9}}\\ \sin(x)&= \pm\dfrac{\sqrt5}{3}\end{align}||
There are therefore 2 possible solutions for |\sin(x),| i.e., |x=\dfrac{\sqrt5}{3}| and |x=-\dfrac{\sqrt5}{3}.| However, the problem specifies that |x| is an angle between |0| and |\dfrac{\pi}{2},| which means it is situated in the 1st quadrant of the unit circle. In this quadrant, all trigonometric ratios are positive. The solution is therefore |\sin(x)=\dfrac{\sqrt5}{3}.|
c) To find the value of |\cot(x),| we use the definition |\cot(x)= \dfrac{\cos(x)}{\sin(x)}.| We replace |\cos(x)| with |\dfrac{2}{3}| and |\sin(x)| with |\dfrac{\sqrt5}{3},| as we just calculated.
||\begin{align}\cot(x) &= \dfrac{\cos(x)}{\sin(x)}\\ &=\dfrac{\dfrac{2}{3}}{\dfrac{\sqrt5}{3}}\\&=\dfrac{2}{3}\times \dfrac{3}{\sqrt5}\\ &=\dfrac{2}{\sqrt5}\end{align}||
Lastly, we need to rationalize the fraction so that the solution respects mathematical conventions. ||\begin{align}\cot(x)&=\dfrac{2\ \boldsymbol{\color{#3a9a38}{(\sqrt{5})}}}{\sqrt{5}\ \boldsymbol{\color{#3a9a38}{(\sqrt{5})}}}\\&=\dfrac{2\sqrt{5}}{5}\end{align}||
d) To find the value of |\tan(-x),| we use the definition |\tan(-x)= \dfrac{\sin(-x)}{\cos(-x)}.| Next, we use the basic trigonometric identities |\cos(-x)=\cos(x)| and |\sin(-x)=-\sin(x).|
||\begin{align}\tan(-x) &= \dfrac{\sin(-x)}{\cos(-x)}\\[3pt] &=\dfrac{-\sin(x)}{\cos(x)}\end{align}||
Now, we replace |\cos(x)| with |\dfrac{2}{3}| and |\sin(x)| with |\dfrac{\sqrt5}{3},| which we calculated in part b).
||\begin{align}\tan(-x)&=\dfrac{-\sin(x)}{\cos(x)}\\[3pt]&=\dfrac{-\dfrac{\sqrt5}{3}}{\dfrac{2}{3}}\\[3pt]&=-\dfrac{\sqrt5}{3}\times\dfrac{3}{2}\\[3pt]&=-\dfrac{\sqrt5}{2}\end{align}||
Solve the following equation:||\tan^2(x)-3\sec(x)\tan(x)-\sec^2(x)=-1||
-
Use the Pythagorean trigonometric identities.
By using the identity |1+\tan^2(x)=\sec^2(x),| we can replace |\tan^2(x)| by |\sec^2(x)-1.|
||\begin{align}\boldsymbol{\color{#3b87cd}{\tan^2(x)}}-3\sec(x)\tan(x)-\sec^2(x)&=-1\\[3pt] \boldsymbol{\color{#3b87cd}{\sec^2(x)-1}}-3\sec(x)\tan(x)-\sec^2(x)&=-1\\[3pt] -3\sec(x)\tan(x)&=0\\[3pt] \sec(x)\tan(x)&=0 \end{align}||
-
Use the definitions of the trigonometric ratios.
This allows the whole equation to be rewritten in terms of sine and cosine. ||\begin{align}\sec(x)\tan(x)&=0\\ \dfrac{1}{\cos(x)} \dfrac{\sin(x)}{\cos(x)}&=0\\ \dfrac{\sin(x)}{\cos^2(x)}&=0 \end{align}|| -
Set the restrictions.
As soon as fractions are involved, we must ensure that each denominator is not equal to |0.| ||\begin{alignat}{1} \cos^2(&x)&&\ne 0\\ &\!\!\Downarrow\\ \cos(&x)&&\ne 0\\ &\!\!\Downarrow\\[-20pt] &x &&\ne \left\lbrace\dots,\dfrac{\pi}{2},\dfrac{3\pi}{2},\dots\right\rbrace \end{alignat}|| -
Use the unit circle to determine the solutions.
For the fraction |\dfrac{\sin(x)}{\cos^2(x)}| to be equal to |0,| the numerator must be zero. Referring to the unit circle, we know that |\sin(x)=0| if |x\in\{\dots,\,0,\,\pi,\,2\pi\dots\}.| These values respect the restrictions.
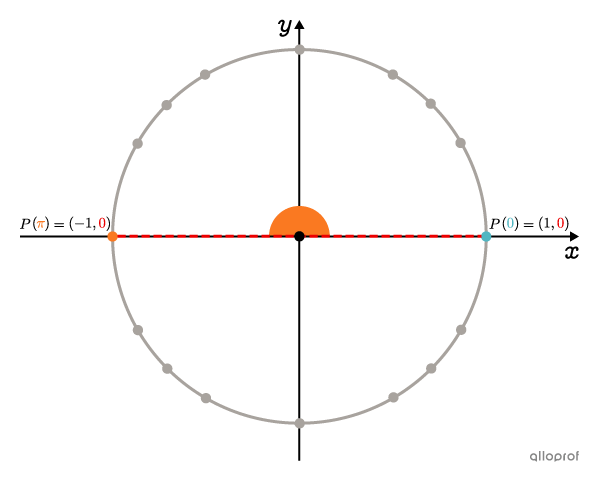
Answer: The solutions of the equation |\tan^2(x)-3\sec(x)\tan(x)-\sec^2(x)=-1| are as follows: ||x\in\{\dots,\,0,\,\pi,\,2\pi\dots\}||
Note: We started by using the Pythagorean identities instead of the definitions of the trigonometric ratios, but it would have worked just as well if we'd done the opposite.
Solve the following equation:||2\sin^2(x)+\cos(2x)+1=0||
-
Use the trigonometric identities of a sum or a difference.
First, we use the identity |\cos(2A)=\cos^2(A)-\sin^2 (A).|
||\begin{align}2\sin^2(x)+\boldsymbol{\color{#3b87cd}{\cos(2x)}}+1&=0\\ 2\sin^2(x)+\boldsymbol{\color{#3b87cd}{\cos^2(x)-\sin^2(x)}}+1&=0\\ \sin^2(x)+\cos^2(x)+1&=0\end{align}||
-
Use the Pythagorean trigonometric identities||\begin{align}\boldsymbol{\color{#3b87cd}{\sin^2(x)+\cos^2(x)}}+1&=0\\ \boldsymbol{\color{#3b87cd}{1}}+1&=0\\ 2&=0\end{align}||We get an equality that is false. This means that the original equation has no solutions.
Answer: The equation |2\sin^2(x)+\cos(2x)+1=0| has no solution.
Note: When we get a trivial equality like |0=0,| it means that the equation has an infinite number of solutions, meaning that all real values of |x| are solutions of the original equation.
We also use the trigonometric identities of a sum or a difference to calculate the exact value of a trigonometric ratio.
Solve the following equation:||\sin(x)\cos(x)=2\cos(x)||
-
Use factoring to reduce the equation to a product of factors equal to |0.|
Subtract |2 \cos(x)| from both sides of the equation. ||\sin(x)\cos(x) - 2\cos(x)= 0||
Remove the greatest common factor |\cos(x).| ||\cos(x)\Big(\!\sin(x) - 2\Big) =0|| Careful! You might be tempted to divide both sides of the equation by |\cos(x)| to simplify it, but you shouldn't do this. This would change the degree of the equation, and eliminate solutions. -
Apply the zero product property.
The product is equal to |0| if |\cos(x)=0| or if |\sin(x)-2=0.| We're left with 2 equations to solve.
|\boldsymbol{\cos(x)=0}|
Since |\boldsymbol{\color{#333fb1}{0}}| is an x-coordinate of one of the main points, we can determine the angles sought directly from the unit circle.

We find that the angles with an x-coordinate of |\boldsymbol{\color{#333fb1}{0}}| are |\boldsymbol{\color{#fa7921}{\dfrac{\pi}{2}}}| and |\boldsymbol{\color{#51b6c2}{\dfrac{3\pi}{2}}}.|
The period of the cosine function is |2\pi,| so the solutions to the equation |\cos(x)=0| are |x\in \left\lbrace \dfrac{\pi}{2} + 2\pi n,\ \dfrac{3\pi}{2} + 2 \pi n \right\rbrace,| where |n\in\mathbb{Z}.|
|\boldsymbol{\sin(x)-2=0}|
We isolate the sine ratio. ||\begin{align}\sin(x)-2&=0\\ \sin(x) &=2\end{align}|| This equation has no solution, because the sine of an angle is always between |-1| and |1| inclusively and here, |2\not\in[-1,1].|
Answer: The solutions of the equation |\sin(x)\cos(x)=2\cos(x)| are as follows:
||x\in\left\lbrace \dfrac{\pi}{2} + 2\pi n,\ \dfrac{3\pi}{2} + 2 \pi n \right\rbrace|| where |n\in\mathbb{Z}|
Solve the following equation:||15\sin(x)\cos(x)-2=5\sin(x)-6\cos(x)||
-
Use factoring to reduce the equation to a product of factors equal to |\boldsymbol{0}.|
We bring all terms to the same side of the equals sign.
||\begin{align}15\sin(x)\cos(x)-2&=5\sin(x)-6\cos(x)\\15\sin(x)\cos(x)-5\sin(x)+6\cos(x)-2&=0\end{align}||
We use factoring by grouping.
||\begin{align}15\sin(x)\cos(x)-5\sin(x)+6\cos(x)-2&=0\\ 5\sin(x)\big(3\cos(x)-1\big)+2\big(3\cos(x)-1\big)&=0\\ \big(3\cos(x)-1\big)\big(5\sin(x)+2\big)&=0\end{align}||
-
Apply the zero product property.
The product is equal to |0| if either of the 2 factors equals |0.| We're left with 2 equations to solve.
|\boldsymbol{3\cos(x)-1=0}|
We isolate the cosine ratio. ||\begin{align} 3\cos(x)-1&=0\\ 3\cos(x)&=1\\ \cos(x)&=\dfrac{1}{3} \end{align}|| The 1st |x|-value is found using |\arccos,| then the 2nd value is its opposite value. ||\begin{align}\cos(x)&=\dfrac{1}{3}\\x&=\arccos\left(\dfrac{1}{3}\right)\\ x_1&\approx1.23\quad\text{et}\quad x_2\approx-1.23 \end{align}|| The period of the function |y=3\cos(x)-1| is |2\pi,| so the solutions of the equation |3\cos(x)-1=0| are |x\in \left\lbrace -1.23 + 2\pi n;\ 1.23 + 2 \pi n \right\rbrace,| where |n\in\mathbb{Z}.|
|\boldsymbol{5\sin(x)+2=0}|
We isolate the sine ratio.||\begin{align}5\sin(x)+2&=0\\ 5\sin(x)&=-2\\ \sin(x)&=\dfrac{-2}{5}\end{align}|| The 1st x-value is found using |\arcsin,| then get the 2nd value by subtracting |x_1| from |\pi.| ||\begin{align}\sin(x)&=\dfrac{-2}{5}\\ x&=\arcsin\left(\dfrac{-2}{5}\right)\end{align}|| ||\begin{aligned}x_1\approx -0.41\quad\text{and}\\\\ \end{aligned} \quad \begin{aligned}x_2&\approx\pi--0.41\\ &\approx3.55 \end{aligned}|| The period of the function |y=5\sin(x)+2| is |2\pi,| so the solutions of the equation |5\sin(x)+2=0| are |x\in \left\lbrace -0.41 + 2\pi n;\ 3.55 + 2 \pi n \right\rbrace,| where |n\in\mathbb{Z}.|
Answer: The solutions of the equation |15\sin(x)\cos(x)-2=5\sin(x)-6\cos(x)| are as follows:
||x\in\left\lbrace -1.23+2\pi n,\, -0.41+2\pi n,\, 1.23+2\pi n,\, 3.55+2\pi n\right\rbrace,|| where |n\in\mathbb{Z}|
Solve the following equation:||3\tan(x)+\cot(x)=5\,\text{cosec}(x)||
Résous l'équation suivante.||3\tan(x)+\text{cotan}(x)=5\,\text{cosec}(x)||
-
Use the definitions of the trigonometric ratios.
This allows the entire equation to be rewritten in terms of sine and cosine.||\begin{alignat}{13} 3\tan(x)&+\cot(x)&&=5\,\text{cosec}(x)\\[3pt] 3\dfrac{\sin(x)}{\cos(x)}&+\dfrac{\cos(x)}{\sin(x)}&&=\dfrac{5}{\sin(x)} \end{alignat}||
-
Set the restrictions.
As soon as fractions are involved, we must ensure that each denominator is not equal to |0.|
||\begin{alignat}{13} \cos&(x)&&\ne0\\[3pt]&\,\Downarrow\\ &\ \ x&&\ne\left\{\dots,\dfrac{\pi}{2},\dfrac{3\pi}{2},\dots\right\}\end{alignat}||
||\begin{alignat}{13}\sin&(x)&&\ne0\\&\,\Downarrow\\&\ \ x&&\ne\{\dots, 0,\,\pi,\,2\pi,\dots\}\end{alignat}||
To sum up, |x| must not be equal to |\left\{\dots,\,0,\,\dfrac{\pi}{2},\,\pi,\,\dfrac{3\pi}{2},\,2\pi,\,\dots\right\}.|
-
Rewrite the fractions using a common denominator.
To find the common denominator, we can multiply the denominators together. So, the common denominator is |\cos(x)\sin(x).| Therefore, we must multiply the 1st fraction by |\dfrac{\sin(x)}{\sin(x)}| and the 2 others by |\dfrac{\cos(x)}{\cos(x)}.|
||\begin{align}\dfrac{3\sin(x)}{\cos(x)}+\dfrac{\cos(x)}{\sin(x)}&=\dfrac{5}{\sin(x)}\\[3pt]\dfrac{3\sin(x)}{\cos(x)}\times\dfrac{\sin(x)}{\sin(x)}+\dfrac{\cos(x)}{\sin(x)}\times\dfrac{\cos(x)}{\cos(x)}&=\dfrac{5}{\sin(x)}\times\dfrac{\cos(x)}{\cos(x)}\\[3pt]\dfrac{3\sin^2(x)}{\cos(x)\sin(x)}+\dfrac{\cos^2(x)}{\cos(x)\sin(x)}&=\dfrac{5\cos(x)}{\cos(x)\sin(x)}\end{align}||
Multiplying both sides of the equation by |\cos(x)\sin(x),| we get the following equation: ||3\sin^2(x) + \cos^2(x) = 5\cos(x)||
-
Use the Pythagorean trigonometric identities.
Using the identity |\cos^2(x) + \sin^2(x)=1,| it is possible to replace |\sin^2(x)| with |1-\cos^2(x).|
||\begin{align} 3\boldsymbol{\color{#3b87cd}{\sin^2(x)}}+ \cos^2(x) &= 5\cos(x)\\ 3\!\boldsymbol{\color{#3b87cd}{\left(1-\cos^2 (x)\right)}} + \cos^2(x) &= 5\cos(x)\end{align}||
All that is left is to simplify the equation and bring all the terms to the same side of the equal sign. ||\begin{align} 3-3\cos^2 (x) + \cos^2(x) &= 5\cos(x) \\3-2\cos^2 (x)&=5\cos(x)\\3-2\cos^2(x) -5\cos(x)&=0\end{align}||
-
Perform a change of variables.
By setting |\cos(x)= z,| we get |-2z^2 -5z + 3=0.| We'll temporarily set aside the cosine ratios to concentrate on solving the 2nd-degree equation.
-
Factor and apply the zero product property.
We need to factor the trinomial |-2z^2 -5z + 3.| We can use the product-sum method to do so.
We are looking for 2 numbers for which the product is |-2\times 3=-6| and for which the sum is |-5.| These numbers are |1| and |-6.|
We rewrite the trinomial by decomposing the term |-5z.| ||-2z^2 \boldsymbol{\color{#3b87cd}{-5z}} + 3\\-2z^2\boldsymbol{\color{#3b87cd}{+1z-6z}}+3||
We use factoring by grouping. ||-2z^2+1z-6z+3\\ z(-2z+1)+3(-2z+1)\\(-2z+1)(z+3)|| We apply the zero product property. This algebraic expression is equal to |0| if |-2z+1=0| or if |z+3=0.| ||\begin{align}\begin{aligned}-2z+1&=0\\-2z&=-1\\ z_1&=\dfrac{1}{2}\end{aligned}\qquad \begin{aligned}z+3&=0\\ z_2&=-3 \\ \phantom{\dfrac{1}{2}} \end{aligned}\end{align}||
The solutions of the equation |-2z^2-5z+3=0| are therefore |z_1=\dfrac{1}{2}| and |z_2=-3.|
Since we made a change of variable, we can substitute |z| with |\cos(x).| We then obtain 2 new equations: |\cos(x)=\dfrac{1}{2}| and |\cos(x)=-3.|
The equation |\cos(x)=-3| has no solution, because the cosine of an angle must always be between |-1| and |1| inclusively and here |-3\not\in[-1,1].|
-
Use the unit circle to determine the solutions.
Since |\boldsymbol{\color{#333fb1}{\dfrac{1}{2}}}| is an x-coordinate of one of the main points, we can determine the angles sought directly from the unit circle.
We find that the angles for which the x-coordinate is |\boldsymbol{\color{#333fb1}{\dfrac{1}{2}}}| are |\boldsymbol{\color{#fa7921}{\dfrac{\pi}{3}}}| and |\boldsymbol{\color{#51b6c2}{\dfrac{5\pi}{3}}}.| So, |x = \dfrac{\pi}{3}| or |x=\dfrac{5\pi}{3}.| Both of these values respect the restrictions.
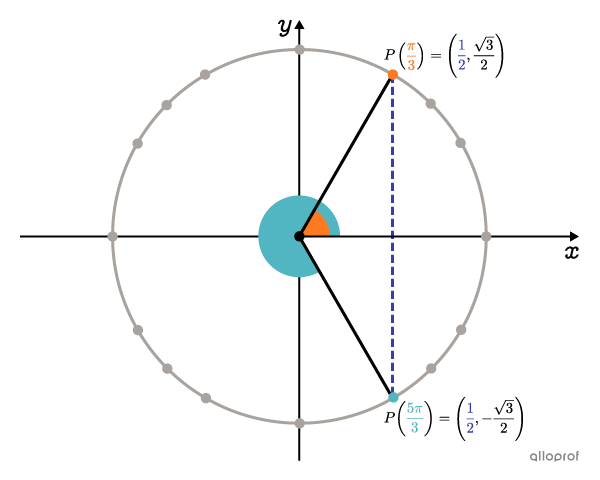
-
Calculate the period and give the solutions.
Since we found our trigonometric angles from a cosine function where |b=1,| we use the basic period of sinusoidal functions, |2\pi.|
Answer: The solutions of the equation |3\tan(x)+\cot(x)=5\,\text{cosec}(x)| are as follows:
||x\in\left\lbrace \dfrac{\pi}{3} + 2\pi n, \dfrac{5\pi}{3} + 2\pi n \right\rbrace,|| where |n\in\mathbb{Z}|
To solve a trigonometric inequality, we use the same strategies as for solving a trigonometric equation. Then, once we have the solutions to the equation, we find the solution set of the inequation by testing values located on either side of the solutions found.
Also, always pay particular attention to the boundaries of the intervals of the solution set.
-
If the inequality sign is |<| or |>,| the boundaries are excluded.
-
If the inequality sign is |\leq| or |\geq,| the boundaries are included.
-
When a boundary corresponds to an asymptote (for the tangent function), it is always excluded.
Solve the following equation:||2\tan(x)+4\sec(x)\le 3\sin(x)+6||
-
Change the inequality symbol to an equals sign.
||\begin{align}2\tan(x)+4\sec(x)&\le 3\sin(x)+6\\ &\downarrow\\ 2\tan(x)+4\sec(x)&= 3\sin(x)+6\end{align}||
-
Use the definitions of the trigonometric ratios.
This allows the entire equation to be rewritten in terms of sine and cosine.||\begin{align} 2\dfrac{\sin(x)}{\cos(x)}+4\dfrac{1}{\cos(x)}&= 3\sin(x)+6\\[3pt]\dfrac{2\sin(x)+4}{\cos(x)}&= 3\sin(x)+6\end{align}||
-
Set the restrictions.
As soon as fractions are involved, we must ensure that each denominator is not equal to |0.| ||\begin{alignat}{13} \cos&(x)&&\ne0\\[3pt]&\,\Downarrow\\ &\ \ x&&\ne\left\{\dots,\dfrac{\pi}{2},\dfrac{3\pi}{2},\dots\right\}\end{alignat}||
-
Use factoring to reduce the equation to a product of factors equal to |0.|
We multiply both sides of the equation by |\cos(x).| We get the following equation: ||2\sin(x)+4= 3\sin(x)\cos(x)+6\cos(x)|| We subtract |2\sin(x)+4| from both sides.
||0= 3\sin(x)\cos(x)+6\cos(x)-2\sin(x)-4|| We factor by grouping. ||\begin{align}0&= 3\sin(x)\cos(x)+6\cos(x)-2\sin(x)-4\\ 0&= 3\cos(x)\big(\!\sin(x)+2\big)-2\big(\!\sin(x)+2\big)\\ 0&=\big(\!\sin(x)+2\big)\big(3\cos(x)-2\big)\end{align}||
-
Apply the zero product property.
The product is equal to |0| if |\sin(x)+2=0| or if |3\cos(x)-2=0.| This gives us 2 equations to solve.
|\boldsymbol{\sin(x)+2=0}|
We isolate the sine ratio.||\begin{align}\sin(x)+2&=0\\ \sin(x) &=-2\end{align}|| This equation has no solution, because the sine of an angle is always between |-1| and |1| inclusively and here|2\not\in[-1,1].|
|\boldsymbol{3\cos(x)-2=0}|
We isolate the cosine ratio.||\begin{align} 3\cos(x)-2&=0\\ 3\cos(x)&=2\\ \cos(x)&=\dfrac{2}{3} \end{align}|| The 1st |x|-value is found using |\arccos,| then the 2nd value is its opposite value. ||\begin{align}\cos(x)&=\dfrac{2}{3}\\x&=\arccos\left(\dfrac{2}{3}\right)\\ x_1&\approx 0.84\quad\text{et}\quad x_2\approx-0.84 \end{align}|| The period of the function |y=3\cos(x)-2| is |2\pi,| so the solutions of the equation |3\cos(x)-2=0| are |x\in \left\lbrace -0.84 + 2\pi n,\ 0.84 + 2 \pi n \right\rbrace,| where |n\in\mathbb{Z}.|
-
Give the solution set of the inequality.
To determine which intervals are part of the solution set, place the solutions of the equation found in Step 5 and the restrictions found in Step 3 on a number line.
In ascending order, the first value is |x_2=-0.84.| Next, we have the value |x_1=0.84.| Then we have a restriction at |x=\dfrac{\pi}{2}\approx 1.57| and another at |x=\dfrac{3\pi}{2}\approx 4.71.| Finally, we see a value that is equivalent to |x_2,| just one period later: |x_3\approx -0.84+2\pi\approx 5.44.|

There are therefore 4 possible intervals, i.e., the one between |-0.84| and |0.84,| the one between |0.84| and |\dfrac{\pi}{2},| the one between |\dfrac{\pi}{2}| and |\dfrac{3\pi}{2},| and the one between |\dfrac{3\pi}{2}| and |5.44.| To determine which intervals are part of the solution set, we can test one |x| value in each interval.
Note: Since the inequality sign is |\le,| the boundaries of the interval are included in the solution set. The restrictions, however, are not.
||\left[\boldsymbol{\color{#51b6c2}{-0.84},\ \boldsymbol{\color{#fa7921}{0.84}}}\right]||
Let’s test |x=0.| ||\begin{align}2\tan(x)+4\sec(x)&\le 3\sin(x)+6\\[3pt] 2\tan(x)+\dfrac{4}{\cos(x)}&\le 3\sin(x)+6\\[3pt] 2\tan(0)+\dfrac{4}{\cos(0)}&\overset{\text{?}}{\le} 3\sin(0)+6\\[3pt] 2\times 0+\dfrac{4}{1}&\overset{\text{?}}{\le} 3\times 0+6\\[3pt] 4&\color{#3a9a38}{\le}6\end{align}|| This inequality is true, which means that the interval |\left[\boldsymbol{\color{#51b6c2}{-0.84},\ \boldsymbol{\color{#fa7921}{0.84}}}\right]| is part of the solution set.
||\left[\boldsymbol{\color{#fa7921}{0.84}},\ \boldsymbol{\color{#ec0000}{\dfrac{\pi}{2}}}\right[||
Let’s test |x=1.| ||\begin{align}2\tan(x)+4\sec(x)&\le 3\sin(x)+6\\[3pt] 2\tan(x)+\dfrac{4}{\cos(x)}&\le 3\sin(x)+6\\[3pt] 2\tan(1)+\dfrac{4}{\cos(1)}&\overset{\text{?}}{\le} 3\sin(1)+6\\[3pt] 2\times 1.56+\dfrac{4}{0.54}&\overset{\text{?}}{\le} 3\times 0.84+6\\[3pt] 10.52&\color{#ec0000}{\not\le}8.52\end{align}|| This inequality is false, which means that the interval |\left[\boldsymbol{\color{#fa7921}{0.84}},\ \boldsymbol{\color{#ec0000}{\dfrac{\pi}{2}}}\right[| is not part of the solution set.
||\left]\boldsymbol{\color{#ec0000}{\dfrac{\pi}{2}}},\boldsymbol{\color{#ec0000}{\dfrac{3\pi}{2}}}\right[||
Let’s test |x=\pi.| ||\begin{align}2\tan(x)+4\sec(x)&\le 3\sin(x)+6\\[3pt] 2\tan(x)+\dfrac{4}{\cos(x)}&\le 3\sin(x)+6\\[3pt] 2\tan(\pi)+\dfrac{4}{\cos(\pi)}&\overset{\text{?}}{\le} 3\sin(\pi)+6\\[3pt] 2\times 0+\dfrac{4}{-1}&\overset{\text{?}}{\le} 3\times 0+6\\[3pt] -4&\color{#3a9a38}{\le}6\end{align}|| This inequality is true, which means that the interval |\left]\boldsymbol{\color{#ec0000}{\dfrac{\pi}{2}}},\boldsymbol{\color{#ec0000}{\dfrac{3\pi}{2}}}\right[|| is part of the solution set.
||\left]\boldsymbol{\color{#ec0000}{\dfrac{3\pi}{2}}},\ \boldsymbol{\color{#51b6c2}{5.44}}\right]||
Let’s test |x=5.| ||\begin{align}2\tan(x)+4\sec(x)&\le 3\sin(x)+6\\[3pt] 2\tan(x)+\dfrac{4}{\cos(x)}&\le 3\sin(x)+6\\[3pt] 2\tan(5)+\dfrac{4}{\cos(5)}&\overset{\text{?}}{\le} 3\sin(5)+6\\[3pt] 7.34&\color{#ec0000}{\not\le}3.12\end{align}|| This inequality is false, which means that the interval ||\left]\boldsymbol{\color{#ec0000}{\dfrac{3\pi}{2}}},\ \boldsymbol{\color{#51b6c2}{5.44}}\right]|| is not part of the solution set.
Answer: Since the boundaries of the interval repeat themselves in every period |(2\pi),| the solution set of the inequality |2\tan(x)+4\sec(x)\le 3\sin(x)+6| is as follows:
||x\in\Big[-0.84+2\pi n,\ 0.84+2\pi n\Big]\ \cup\ \left]\dfrac{\pi}{2}+2\pi n,\dfrac{3\pi}{2}+2\pi n\right[,|| where |n\in\mathbb{Z}|
Solve the following inequality: ||2\cos^2(x)<1-\sin(x)||
-
Change the inequality symbol to an equal sign.
||\begin{align}2\cos^2(x)&<1-\sin(x)\\ &\downarrow\\ 2\cos^2(x)&=1-\sin(x)\end{align}||
-
Use the Pythagorean trigonometric identities.
Using the identity |\cos^2(x) + \sin^2(x)=1,| it’s possible to replace |\cos^2(x)| with |1-\sin^2(x).| ||\begin{align}2\boldsymbol{\color{#3b87cd}{\cos^2(x)}}&=1-\sin(x)\\2\left(\boldsymbol{\color{#3b87cd}{1-\sin^2(x)}}\right)&=1-\sin(x)\\ 2-2\sin^2(x)&=1-\sin(x)\\ 0&=2\sin^2(x)-\sin(x)-1\end{align}||
-
Perform a change of variables.
By setting |\sin(x)= z,| we get |2z^2 -z -1=0.| We'll temporarily set aside the sine ratios to concentrate on solving the 2nd-degree equation.
-
Use factoring and apply the zero product property.
We need to factor the trinomial |2z^2 -z -1.| We can use the product-sum method to do so. We are looking for 2 numbers for which the product is |2\times -1=-2| and for which the sum is |-1.| These numbers are |1| and |-2.|
We rewrite the trinomial by decomposing the term |-z.| ||2z^2 \boldsymbol{\color{#3b87cd}{-z}}-1\\ 2z^2\boldsymbol{\color{#3b87cd}{-2z+z}}-1|| We factor by grouping.
||2z^2-2z+z-1\\2z(z-1)+1(z-1)\\(z-1)(2z+1)|| We apply the zero product property. This algebraic expression is equal to |0| if |z-1=0| or if |2z+1=0.| ||\begin{align}\begin{aligned}z-1&=0\\z_1&=1\\ \phantom{\dfrac{1}{2}}\end{aligned}\qquad \begin{aligned}2z+1&=0\\ 2z&=-1\\ z_2&=-\dfrac{1}{2} \end{aligned}\end{align}|| The solutions of the equation |2z^2-z-1=0| are therefore |z_1=1| and |z_2=-\dfrac{1}{2}.| Since we made a change of variable, we can substitute |z| with |\sin(x).| We then obtain 2 new equations: |\sin(x)=1| and |\sin(x)=-\dfrac{1}{2}.|
-
Use the unit circle to determine the solutions.
Since |\boldsymbol{\color{#ec0000}{1}}| and |\boldsymbol{\color{#ec0000}{-\dfrac{1}{2}}}| are y-coordinates of main points, we can find the angles sought directly from the unit circle.
We find that the angles when the y-coordinate is |\boldsymbol{\color{#ec0000}{1}}| are |\boldsymbol{\color{#ff55c3}{\dfrac{\pi}{2}}},| and the angles when the y-coordinate is |\boldsymbol{\color{#ec0000}{-\dfrac{1}{2}}}| are |\boldsymbol{\color{#fa7921}{\dfrac{7\pi}{6}}}| and |\boldsymbol{\color{#51b6c2}{\dfrac{11\pi}{6}}}.|
Therefore, |x_1 = \dfrac{\pi}{2},| |x_2=\dfrac{7\pi}{6},| and |x_3=\dfrac{11\pi}{6}.|

-
Give the solution set of the inequality.
There are therefore 3 possible intervals, i.e., the one between |\boldsymbol{\color{#ff55c3}{\dfrac{\pi}{2}}}| and |\boldsymbol{\color{#fa7921}{\dfrac{7\pi}{6}}},| the one between |\boldsymbol{\color{#fa7921}{\dfrac{7\pi}{6}}}| and |\boldsymbol{\color{#51b6c2}{\dfrac{11\pi}{6}}},| and the one between|\boldsymbol{\color{#51b6c2}{\dfrac{11\pi}{6}}}| and the value that is one period further than |\boldsymbol{\color{#ff55c3}{\dfrac{\pi}{2}}}.| To determine which intervals are part of the solution set, we can test one |x| value in each interval.
Note: Since the inequality sign is |<,| the boundaries of the interval are not included in the solution set.
||\left]\boldsymbol{\color{#ff55c3}{\dfrac{\pi}{2}}},\boldsymbol{\color{#fa7921}{\dfrac{7\pi}{6}}}\right[||
Let’s test |x=\pi.| ||\begin{align}2\cos^2(x)&<1-\sin(x)\\[3pt] 2\cos^2(\pi)&\overset{\text{?}}{<}1-\sin(\pi)\\[3pt] 2(-1)^2&\overset{\text{?}}{<}1-0\\[3pt] 2&\color{#ec0000}{\not<}1\end{align}|| This inequality is false, which means that the interval ||\left]\boldsymbol{\color{#ff55c3}{\dfrac{\pi}{2}}},\boldsymbol{\color{#fa7921}{\dfrac{7\pi}{6}}}\right[|| is not part of the solution set.
||\left]\boldsymbol{\color{#fa7921}{\dfrac{7\pi}{6}}}, \boldsymbol{\color{#51b6c2}{\dfrac{11\pi}{6}}}\right[||
Let’s test |x=\dfrac{3\pi}{2}.| ||\begin{align}2\cos^2(x)&<1-\sin(x)\\[3pt] 2\cos^2\left(\dfrac{3\pi}{2}\right)&\overset{\text{?}}{<}1-\sin\left(\dfrac{3\pi}{2}\right)\\2(0)^2&\overset{\text{?}}{<}1--1\\[3pt] 0&\color{#3a9a38}{<}2\end{align}|| This inequality is true, which means that the interval |\left]\boldsymbol{\color{#fa7921}{\dfrac{7\pi}{6}}}, \boldsymbol{\color{#51b6c2}{\dfrac{11\pi}{6}}}\right[| is part of the solution set.
||\begin{align}\left]\boldsymbol{\color{#51b6c2}{\dfrac{11\pi}{6}},\color{#ff55c3}{\dfrac{\pi}{2}}}+p\right[&= \left]\boldsymbol{\color{#51b6c2}{\dfrac{11\pi}{6}},\color{#ff55c3}{\dfrac{\pi}{2}}}+2\pi\right[\\[3pt]&=\left]\boldsymbol{\color{#51b6c2}{\dfrac{11\pi}{6}},\color{#ff55c3}{\dfrac{5\pi}{2}}}\right[\end{align}||
Let’s test |x=2\pi.| ||\begin{align}2\cos^2(x)&<1-\sin(x)\\[3pt] 2\cos^2(2\pi)&\overset{\text{?}}{<}1-\sin(2\pi)\\[3pt] 2(1)^2&\overset{\text{?}}{<}1-0\\[3pt] 2&\color{#ec0000}{\not<}1\end{align}|| This inequality is false, which means that the interval |\left]\boldsymbol{\color{#51b6c2}{\dfrac{11\pi}{6}},\color{#ff55c3}{\dfrac{5\pi}{2}}}\right[| is not part of the solution set.
Answer: Since the boundaries of the interval repeat themselves in every period |(2\pi),| the solution set of the inequality |2\cos^2(x)<1-\sin(x)| is as follows:
||x\in \left]\dfrac{7\pi}{6}+2\pi n,\dfrac{11\pi}{6}+2\pi n\right[,|| where |n\in\mathbb{Z}|