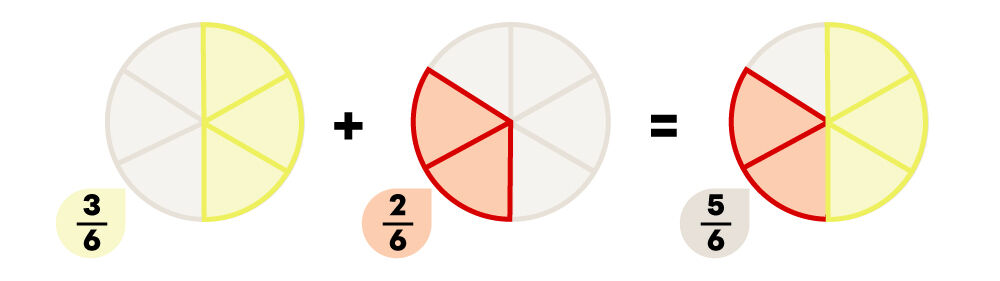
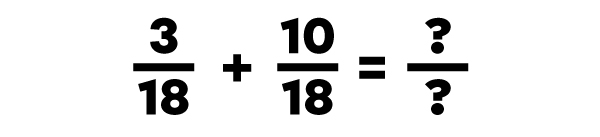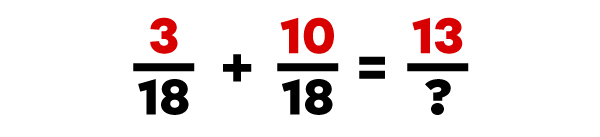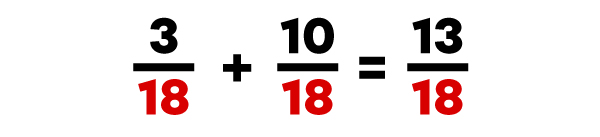Pour faire une addition de fractions dont le dénominateur est commun (identique), tu dois additionner les numérateurs et conserver le même dénominateur pour la réponse.
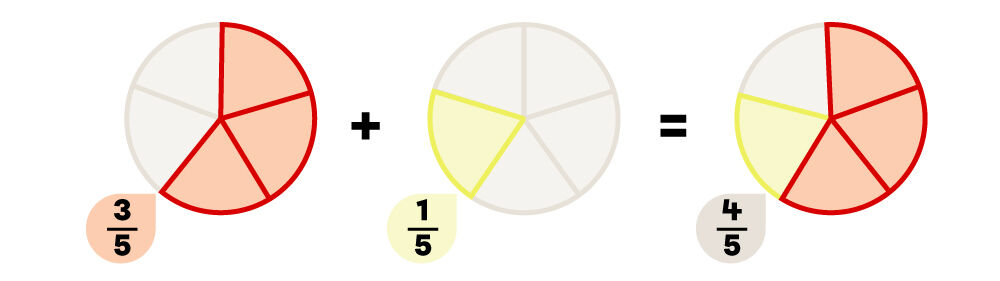
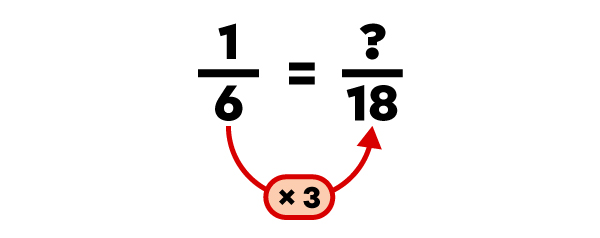
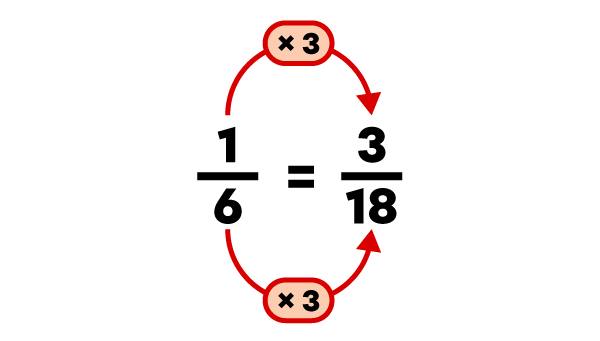
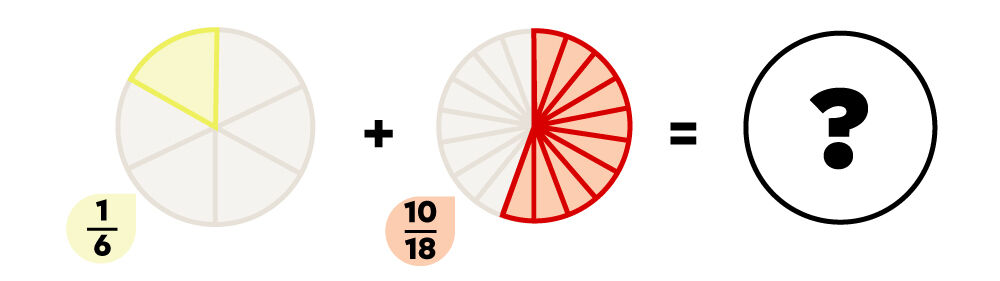
Lorsque les fractions additionnées ont un dénominateur différent, il faut d'abord trouver un dénominateur commun (identique) et ensuite transformer les fractions de façon à ce qu'elles restent équivalentes.
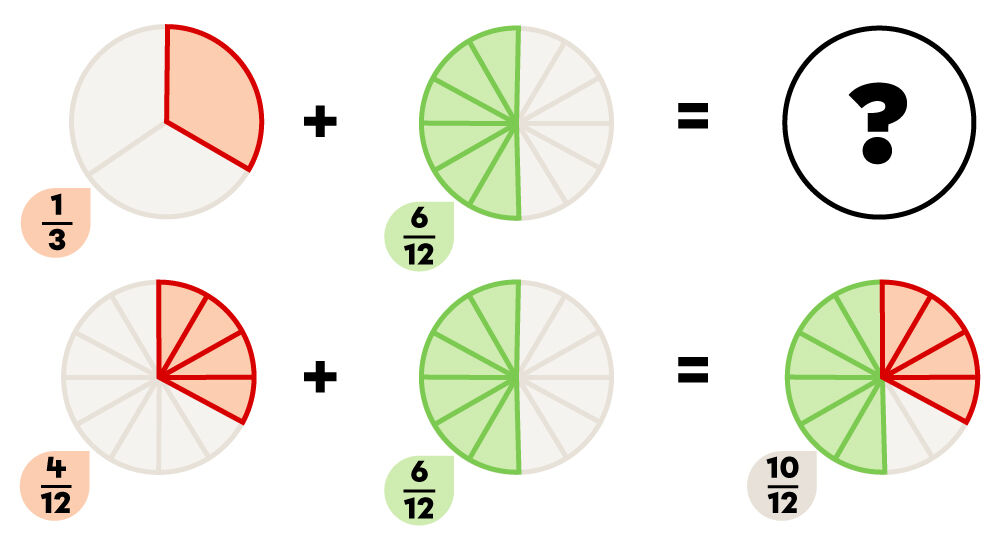
Les fractions |\dfrac{1}{3}| et |\dfrac{6}{12}| peuvent être transformées en fractions équivalentes sur |12|.
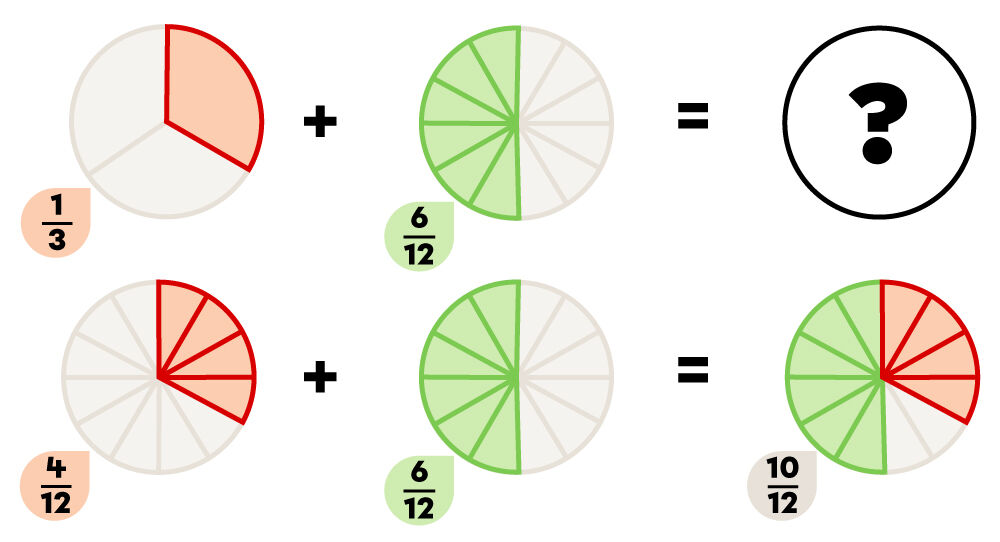
Assure-toi de bien respecter les consignes qui te sont données. Tu peux avoir à écrire la réponse en nombre fractionnaire ou sous la forme d’une fraction irréductible.
|
|
|
|
|
|
|
|
|
|
|
|
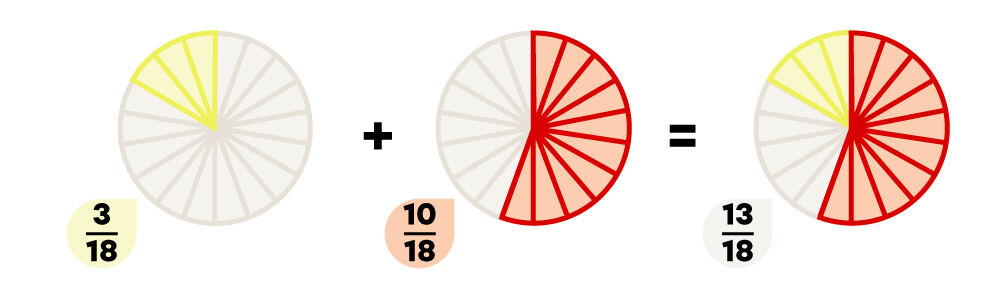
Pour additionner des fractions dont les dénominateurs sont différents à l’aide du plus petit commun multiple (PPCM), il faut d'abord trouver un dénominateur commun (identique) et ensuite transformer les fractions de façon à ce qu'elles restent équivalentes.
Les fractions |\dfrac{1}{3}| et |\dfrac{6}{12}| peuvent être transformées en fractions équivalentes sur |12|.
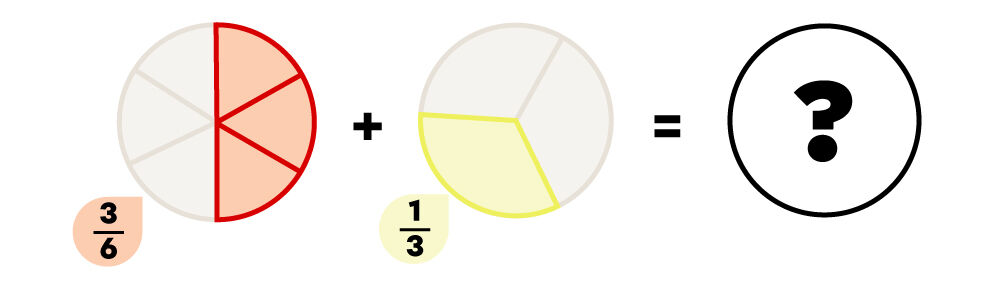
Assure-toi de bien respecter les consignes qui te sont données. Tu peux avoir à écrire la réponse en nombre fractionnaire ou sous la forme d’une fraction irréductible.
|
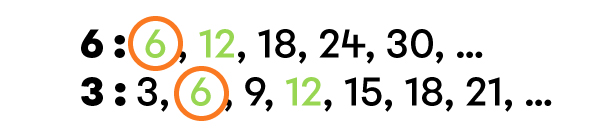 |
|
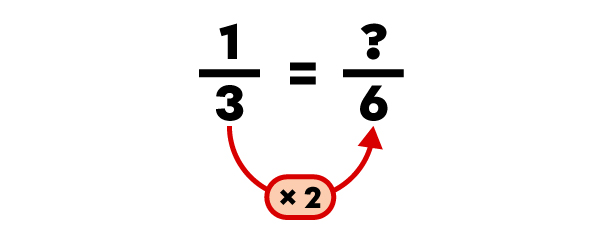 |
|
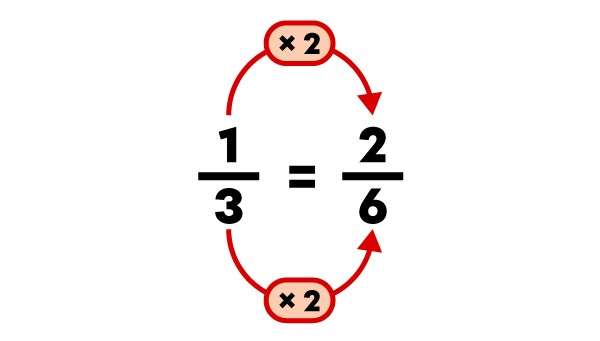 |
|
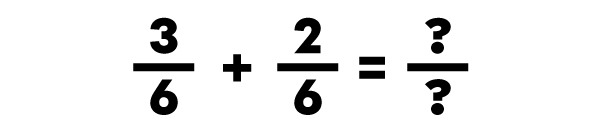 |
|
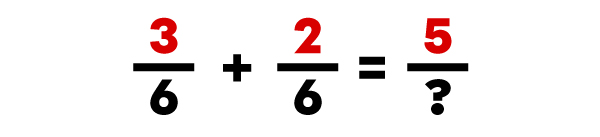 |
|
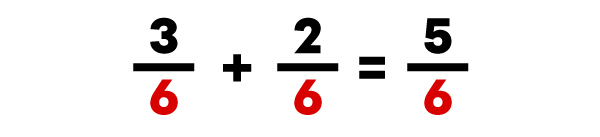 |