Lorsqu’on effectue une addition ou une soustraction de vecteurs, on obtient un nouveau vecteur qu’on appelle vecteur résultant (aussi appelé résultante).
Plusieurs méthodes sont utilisées pour additionner des vecteurs. Lorsque les vecteurs sont dans un plan, on peut utiliser la méthode du triangle ou la méthode du parallélogramme. On peut aussi additionner des vecteurs de façon algébrique à l’aide de la méthode algébrique. Finalement, dans certains cas, on peut utiliser la relation de Chasles.
La somme des vecteurs |\overrightarrow{u}| et |\overrightarrow{v}| est définie par le vecteur résultant suivant.||\overrightarrow{u}+\overrightarrow{v}||
Comme son nom l’indique, la méthode du triangle consiste à obtenir un vecteur résultant en formant un triangle dans un plan cartésien.
-
Placer les vecteurs l'un à la suite de l'autre de façon à ce que l'extrémité du premier vecteur devienne l'origine du second vecteur.
-
Tracer le vecteur résultant en reliant l’origine du premier vecteur à l'extrémité du second vecteur.
Détermine la résultante de la somme des vecteurs suivants.
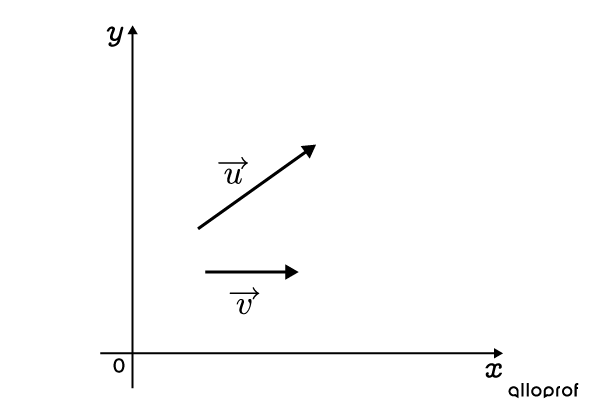
-
Placer les vecteurs l’un à la suite de l’autre
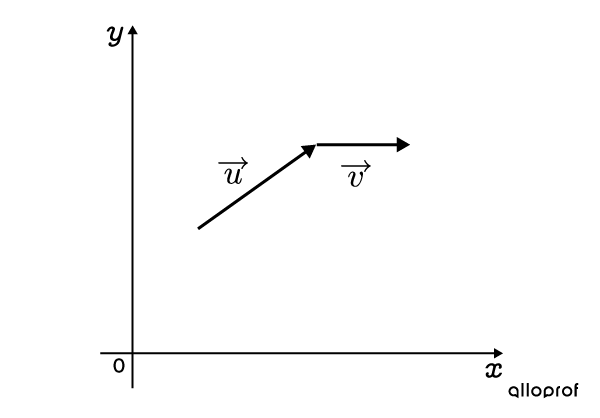
-
Tracer le vecteur résultant

La résultante est le vecteur vert qui a été obtenu à la suite de l'addition de |\overrightarrow {u}| et |\overrightarrow {v}.|
Lorsque les vecteurs ont la même origine, on peut utiliser la méthode du parallélogramme. La résultante est alors la diagonale du parallélogramme ainsi formé.
-
Placer |\overrightarrow{u}| et |\overrightarrow{v}| de sorte qu’ils aient la même origine.
-
Tracer un autre |\overrightarrow{u}| à l'extrémité de |\overrightarrow{v}.|
-
Tracer un autre |\overrightarrow{v}| à l'extrémité de |\overrightarrow{u}.|
-
Tracer le vecteur résultant qui débute à l'origine et qui se rend jusqu'au sommet opposé du parallélogramme ainsi formé.
Détermine la résultante de la somme des vecteurs suivants.
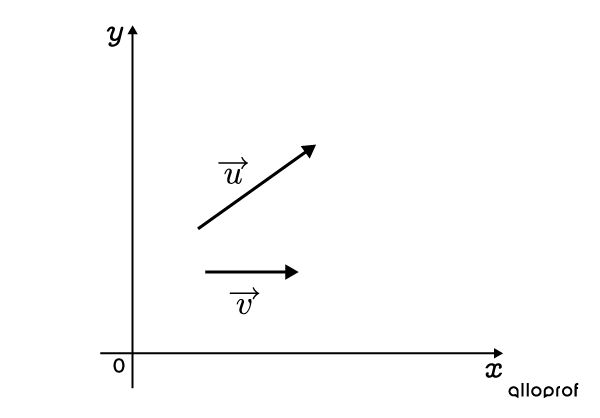
-
Placer |\overrightarrow{u}| et |\overrightarrow{v}| de sorte qu’ils aient la même origine
En déplaçant |\overrightarrow{v},| on obtient la représentation suivante.
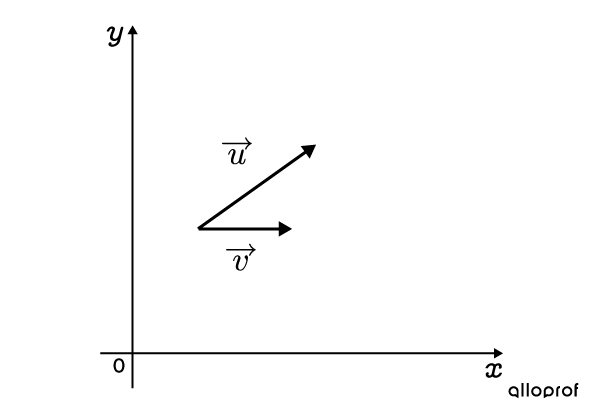
-
Tracer un autre |\overrightarrow{u}| à l'extrémité de |\overrightarrow{v}|
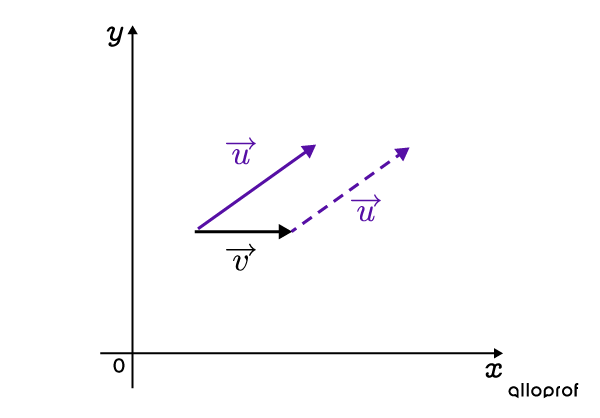
-
Tracer un autre |\overrightarrow{v}| à l'extrémité de |\overrightarrow{u}|
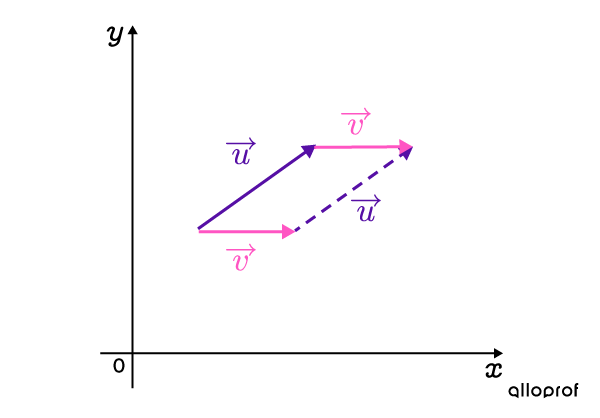
-
Tracer le vecteur résultant

La résultante est le vecteur vert qui a été obtenu à la suite de l'addition de |\overrightarrow {u}| et |\overrightarrow {v}.|
Pour additionner des vecteurs de façon algébrique, on additionne les composantes des vecteurs afin d’obtenir les composantes du vecteur résultant.
Soit |\overrightarrow{u}=(a,b)| et |\overrightarrow{v}=(c,d),| alors :||\begin{align}\overrightarrow {u}+\overrightarrow{v}&= (\color{#EC0000}a,\color{#3B87CD}b)+(\color{#EC0000}c, \color{#3B87CD}d)\\&=(\color{#EC0000}a+\color{#EC0000}c,\color{#3B87CD}b+ \color{#3B87CD}d)\end{align}||
-
Additionner les composantes en |x| et en |y| de chacun des vecteurs.
-
Déduire les composantes du vecteur résultant.
Soit |\overrightarrow{u}=(3, 2)| et |\overrightarrow{v}=(4, -1).| Quelle est la résultante de la somme de ces 2 vecteurs?
-
Additionner les composantes en |x| et en |y| de chacun des vecteurs||\begin{align}\overrightarrow {u}+\overrightarrow{v}&= (\color{#EC0000}3,\color{#3B87CD}2)+(\color{#EC0000}4, \color{#3B87CD}{-1})\\&=(\color{#EC0000}3+\color{#EC0000}4,\color{#3B87CD}2+ \color{#3B87CD}{-1})\\&=(7,1)\end{align}||
-
Déduire les composantes du vecteur résultant
Les composantes |(x,y)| de la résultante sont |(7, 1).|
Pour additionner des vecteurs à l’aide de la relation de Chasles, les points de départ et d’arrivée des vecteurs doivent être identifiés par des lettres. La relation de Chasles est très utile lors des démonstrations vectorielles.
Il est possible d’additionner deux vecteurs à l’aide de la relation de Chasles lorsque l’extrémité du premier vecteur concorde avec l'origine du second vecteur. La somme est alors égale au vecteur ayant comme origine celle du premier et comme extrémité celle du second vecteur.||\overrightarrow{A\color{#FF55C3}{B}}+\overrightarrow{\color{#FF55C3}BC}=\overrightarrow{AC}||
L’exemple suivant présente un cas où il est possible d’appliquer la relation de Chasles.
Quel est le vecteur résultant de l’addition des vecteurs |\overrightarrow{RS}| et |\overrightarrow{TR}|?
On remarque que le premier vecteur a le point |R| comme origine, alors que le second a le point |R| comme extrémité. Comme l'addition des vecteurs est commutative, on peut changer l'ordre de l’addition des vecteurs, ce qui fait en sorte que l’extrémité du premier concorde avec l’origine du second.||\overrightarrow{RS}+\overrightarrow{TR}=\overrightarrow{TR}+\overrightarrow{RS}||On a maintenant la bonne forme pour pouvoir appliquer la relation de Chasles. On obtient :||\overrightarrow{T\color{#FF55C3}{R}}+\overrightarrow{\color{#FF55C3}RS}=\overrightarrow{TS}||La résultante de la somme des vecteurs |\overrightarrow{RS}| et |\overrightarrow{TR}| est le vecteur |\overrightarrow{TS}.|
Soustraire un vecteur revient à additionner son vecteur opposé.
La soustraction de |\overrightarrow{u}| et |\overrightarrow{v}| est :||\overrightarrow{u}-\overrightarrow{v}=\overrightarrow{u}+(-\overrightarrow{v})||Dans cette image, on a représenté l’addition et la soustraction de |\overrightarrow{u}| et |\overrightarrow{v}.|
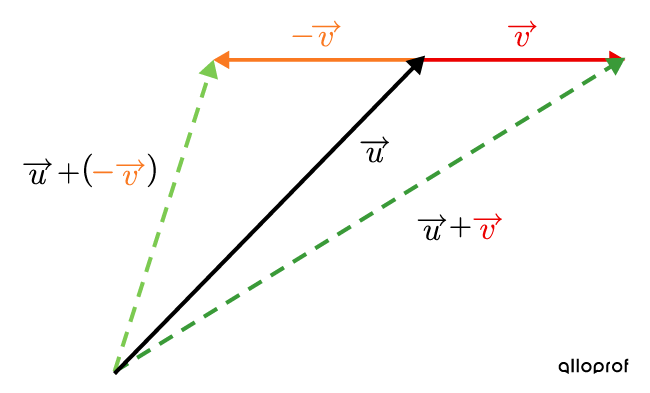
Après avoir changé la soustraction pour une addition, on peut utiliser la méthode du triangle ou du parallélogramme pour obtenir le vecteur résultant dans un plan.
Pour soustraire des vecteurs de façon algébrique, on additionne les composantes du premier vecteur avec l’opposé des composantes du deuxième vecteur.
Soit |\overrightarrow{u}=(a,b)| et |\overrightarrow{v}=(c,d),| alors :||\begin{align}\overrightarrow {u}-\overrightarrow{v}&=\overrightarrow {u}+(-\overrightarrow{v})\\&= (\color{#EC0000}a,\color{#3B87CD}b)+(-\color{#EC0000}c, -\color{#3B87CD}d)\\&=(\color{#EC0000}a-\color{#EC0000}c,\color{#3B87CD}b-\color{#3B87CD}d)\end{align}||
-
Additionner les composantes du premier vecteur avec l’opposé des composantes du deuxième vecteur.
-
Déduire les composantes du vecteur résultant.
Soit le vecteur |\overrightarrow{u}=(3,2)| et le vecteur |\overrightarrow{v}=(4,-1).| Que vaut |\overrightarrow{u}-\overrightarrow{v}|?
-
Additionner les composantes du premier vecteur avec l’opposé des composantes du deuxième vecteur||\begin{align}\overrightarrow {u}-\overrightarrow{v}&=(\color{#EC0000}a,\color{#3B87CD}b)+(-\color{#EC0000}c,-\color{#3B87CD}d)\\&=(\color{#EC0000}3,\color{#3B87CD}2)+(-\color{#EC0000}4,-\color{#3B87CD}{-1})\\&=(\color{#EC0000}3-\color{#EC0000}4,\color{#3B87CD}2+\color{#3B87CD}{1})\\&=(-1,3)\end{align}||
-
Déduire les composantes du vecteur résultant
Les composantes |(x,y)| de la résultante sont |(-1,3).|
En utilisant le point de départ et le point d’arrivée des vecteurs ainsi que la définition de la soustraction des vecteurs, on peut écrire la soustraction comme ceci.||\begin{align}\overrightarrow{AB}-\overrightarrow{CD}&=\overrightarrow{AB}+(-\overrightarrow{CD})\\&=\overrightarrow{AB}+\overrightarrow{DC}\end{align}||Cette dernière écriture permet, dans certains cas, d’utiliser la relation de Chasles.
Quel est le vecteur résultant de la soustraction |\overrightarrow{AC}-\overrightarrow{BC}|?
Comme soustraire revient à additionner le vecteur opposé, on a :||\overrightarrow{AC}-\overrightarrow{BC}=\overrightarrow{AC}+\overrightarrow{CB}||Comme l’extrémité du premier vecteur concorde avec l’origine du second, on peut appliquer la relation de Chasles.||\overrightarrow{A\color{#FF55C3}{C}}+\overrightarrow{\color{#FF55C3}CB}=\overrightarrow{AB}||La résultante de la soustraction des vecteurs |\overrightarrow{AC}| et |\overrightarrow{BC}| est le vecteur |\overrightarrow{AB}.|
Pour valider ta compréhension à propos des vecteurs de façon interactive, consulte la MiniRécup suivante :
