L’aire d’un solide peut être exprimée au moyen d'expressions algébriques. Dans ce cas, les mesures nécessaires pour effectuer les calculs sont exprimées par des monômes ou des polynômes. Pour permettre la résolution de ce type de problème, on utilise un maximum de deux variables pour définir les différentes mesures.
L'aire d'un solide est la surface occupée par ses faces. Il est possible d’exprimer l’aire au moyen d’une expression algébrique si la mesure de ses côtés est exprimée par des variables ou des expressions algébriques. Pour la calculer, on utilise les formules d'aire associées au solide étudié, mais il est également possible d'utiliser les formules d'aire des différentes figures correspondant à chacune de ses faces.
Il arrive que certaines mesures des solides soient manquantes. Dans ces cas, elles sont remplacées par des variables ou des expressions algébriques. Parfois, ces expressions algébriques sont fournies dans leur intégralité alors qu'à d'autres moments, il faut traduire mathématiquement les informations de l'énoncé pour les trouver. En appliquant les formules d'aire, on obtient une expression algébrique simplifiée.
L’exemple ci-dessous présente un problème où les expressions algébriques sont fournies.
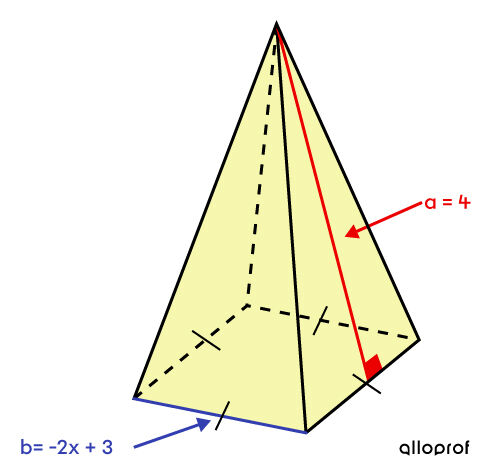
Détermine l’expression algébrique associée à l’aire latérale de la pyramide à base carrée suivante.

-
Identifier les expressions algébriques
Comme il s’agit d’une pyramide à base carrée, on utilise la formule |A_L=\dfrac{P_b\times a}{2}.|
-
Utiliser la formule appropriée et substituer les expressions algébriques ||\begin{align} A_L&=\dfrac{\color{#333FB1}{P_b}\times \color{#EC0000}{a}}{2}\\ &=\dfrac{{\color{#333FB1}{4c}}\times \color{#EC0000}{4}}{2}\\ &=\dfrac{\color{#333FB1}{4(-2x+3)\times \color{#EC0000}{4}}}{2}\end{align}||
-
Simplifier l’expression algébrique ||\begin{align} A_L &= \dfrac{{\color{#333FB1}{4(-2x+3)}}\times \color{#EC0000}{4}}{2} \\ &= \dfrac{\color{#333FB1}{(-8x+12)}\times\cancelto{2}{\color{#EC0000}{4}}}{\cancel{2}}\\ &=(-8x+12)\times2\\ &=-16x+24\end{align}||
-
Interpréter la réponse
L’expression algébrique de l’aire latérale de la pyramide est |-16x+24.|
L’exemple ci-dessous présente un problème où il faut traduire mathématiquement les informations de l'énoncé pour déterminer les expressions algébriques.
Afin de minimiser le cout de production des boites utilisées pour le transport de marchandises, les ingénieurs responsables de ce département savent que les boites, généralement en forme de prisme à base rectangulaire, doivent avoir une hauteur de 5 unités et que la largeur doit mesurer deux unités de moins que le triple de la mesure de la profondeur.
À la lumière de ces informations, détermine l'expression algébrique associée à l'aire totale d'une boite.
-
Si possible, représenter la situation par un dessin
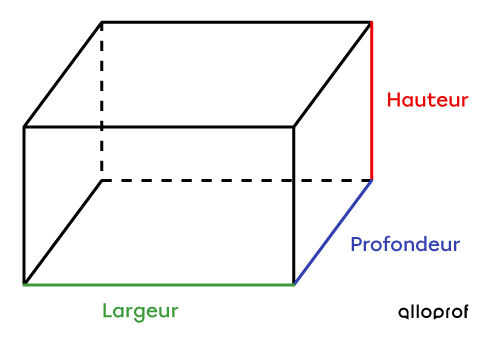
-
Identifier les expressions algébriques
À l'aide de la mise en situation, on peut attribuer la variable à l'une des dimensions, ici la profondeur, et déduire les autres dimensions.
|\begin{align}\color{#EC0000}{h} &= \color{#EC0000}{5}\\\color{#333FB1}{p} &= \color{#333FB1}{x}\\\color{#3A9A38}{l} &= \color{#3A9A38}{3x - 2}\end{align}|
Ainsi, on obtient le dessin suivant :
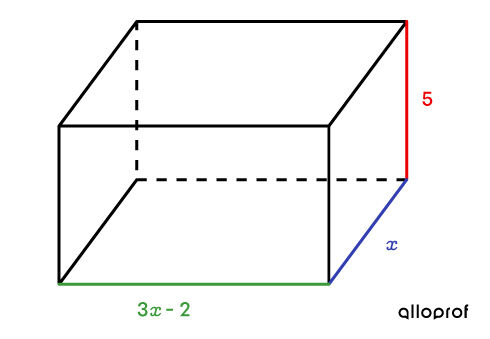
-
Utiliser la formule appropriée et substituer les expressions algébriques ||\begin{align} A_T &= 2 \times A_b &&+&& A_L \\&= 2 \times \color{#3A9A38}{l} \times \color{#333FB1}{p} &&+&& P_b \times \color{#EC0000}{h}\\&=2 \times (\color{#3A9A38}{3x-2}) \times \color{#333FB1}{x} &&+&& (\color{#3A9A38}{3x - 2} + \color{#3A9A38}{3x - 2} + \color{#333FB1}{x} + \color{#333FB1}{x}) \times \color{#EC0000}{5}\end{align}||
-
Simplifier l'expression algébrique ||\begin{align} A_T &= 2 \times (\color{#3A9A38}{3x-2}) \times \color{#333FB1}{x}&&+&& (\color{#3A9A38}{3x - 2} + \color{#3A9A38}{3x - 2} + \color{#333FB1}{x} + \color{#333FB1}{x}) \times \color{#EC0000}{5}\\&= 2\times (3x^2 - 2x) &&+&& (8x - 4)\times \color{#EC0000}{5} \\&= 6x^2 - 4x &&+&& 40x - 20\\&= 6x^2 + 36x -20 \end{align}||
-
Interpréter la réponse
L'expression algébrique de l'aire totale du prisme est |6x^2 + 36x - 20.|
L'utilisation d'expressions algébriques pour représenter la mesure des arêtes permet de généraliser et de résoudre un plus grand nombre de problèmes. On peut appliquer ce raisonnement avec le concept du volume.
Il arrive qu'aucune des mesures d’un solide ne soient connues. Dans ce cas, on peut toujours utiliser des expressions algébriques pour définir les mesures manquantes. L'utilisation de l'algèbre a pour avantage de représenter toutes les réponses possibles.
Quelle est l’expression algébrique associée à la mesure d’un côté de la base de ce prisme sachant que l’aire latérale est de |\color{#3A9A38}{80x^2}|?
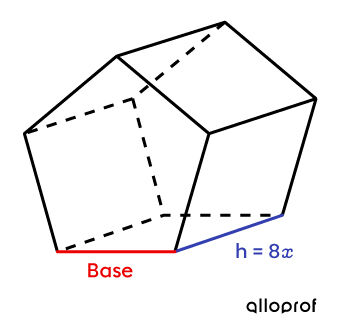
-
Utiliser la formule appropriée
On utilise la formule de l’aire latérale d’un prisme. ||A_L=P_b\times h|| -
Remplacer les valeurs connues ||\begin{align} \color{#3A9A38}{A_L} &= \color{#EC0000}{P_b} \times \color{#333FB1}{h}\\ \color{#3A9A38}{80 x^2} &=\color{#EC0000}{P_b} \times \color{#333FB1}{8x}\end{align}||
-
Trouver l’expression qui représente le périmètre de la base ||\begin{align}80x^2&=P_b\times 8x\\\dfrac{80x^2}{\color{#EC0000}{8x}}&=\dfrac{P_b\times 8x}{\color{#EC0000}{8x}}\\10x&=P_b\end{align}||
-
Déterminer la mesure du côté de la base en utilisant la formule du périmètre ||\begin{align} P_b &= c+c+c+c+c \\ 10x &= 5c \\ \dfrac{10x}{\color{#EC0000}{5}} &= \dfrac{5c}{\color{#EC0000}{5}} \\ 2x &= c \end{align}||
-
Interpréter la réponse
L’expression algébrique associée à la base du prisme est |2x.|
Quelle est l'expression algébrique associée à la hauteur d'un cylindre dont l’aire totale est de |48\pi x^2| et le rayon de la base, de |3x|?
-
Utiliser la formule appropriée
On utilise la formule de l’aire totale d’un cylindre. ||A_T = 2A_b + A_L|| -
Trouver l’expression qui représente l’aire d’une base ||\begin{align} \color{#333FB1}{A_b} &= \pi r^2\\&=\pi (3x)^2\\&=\pi \times 9x^2 \\ &= \color{#333FB1}{9\pi x^2} \end{align}||
-
Remplacer les valeurs connues ||\begin{align} \color{#3A9A38}{A_t} &= 2\color{#333FB1}{A_b} + A_L\\ \color{#3A9A38}{48\pi x^2} &= 2\times \color{#333FB1}{9\pi x^2} + A_L \end{align}||
-
Trouver l’expression qui représente l’aire latérale ||\begin{align} 48\pi x^2&=18\pi x^2+A_L \\ 30\pi x^2&=A_L \end{align}||
-
Déterminer la hauteur en utilisant la formule de l’aire latérale ||\begin{align} A_L &= P_b\times h \\ A_L &= 2\pi r \times h\\30\pi x^2 &= 2\pi(3x)\times h\\30\pi x^2&=6\pi x \times h\\ \dfrac{30\pi x^2}{\color{#EC0000}{6\pi x}} &= \dfrac{6\pi x \times h}{\color{#EC0000}{6\pi x}} \\ 5x &= h\end{align}||
-
Interpréter la réponse
L'expression algébrique associée à la hauteur du cylindre est |5x.|