Le volume d’un solide peut être exprimé au moyen d'expressions algébriques. Dans ce cas, les mesures nécessaires aux calculs sont exprimées par des monômes ou des polynômes. Pour effectuer les calculs dans ce type de problème, on utilise un maximum de 2 variables pour définir les différentes mesures.
Le volume d’un solide correspond à l’espace qu’il occupe. Il est possible d’exprimer le volume au moyen d’une expression algébrique si les mesures du solide sont définies par des variables ou des expressions algébriques. Ainsi, il est important de se référer aux différentes formules de calcul du volume des solides.
Il arrive que certaines mesures des solides soient manquantes. Dans ces cas, elles sont remplacées par des variables ou des expressions algébriques. Parfois, ces expressions algébriques sont fournies dans leur intégralité alors qu'à d'autres moments, il faut traduire mathématiquement les informations de l'énoncé pour les trouver. En appliquant les formules de calcul du volume, on est en mesure d'obtenir une expression algébrique simplifiée.
L’exemple ci-dessous présente un problème où les expressions algébriques sont fournies.
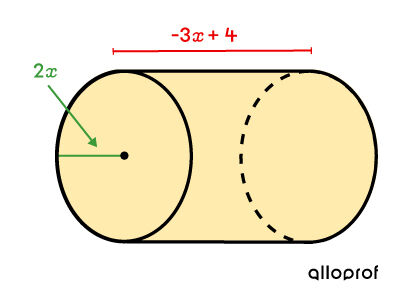
Détermine l’expression algébrique associée au volume du cylindre suivant.
-
Identifier les expressions algébriques
-
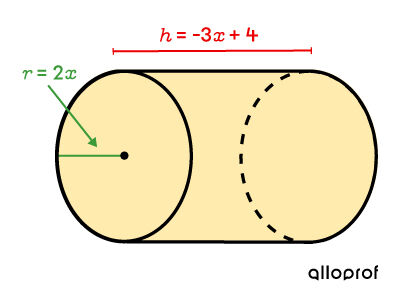
Utiliser la formule appropriée et substituer les expressions algébriques ||V=A_b\times \color{#EC0000}{h}\phantom{\times(-3x+4)}||
Comme la base est un disque, on utilise la formule de l’aire d’un disque : ||\begin{align} V &= A_b \times \color{#EC0000}{h}\\&= \pi \color{#3A9A38}{r}^2\times \color{#EC0000}h\\&=\pi (\color{#3A9A38}{2x})^2\times (\color{#EC0000}{-3x+4}) \end{align}|| -
Simplifier l’expression algébrique ||\begin{align} V&=\pi (\color{#3A9A38}{2x})^2\times (\color{#EC0000}{-3x+4})\\&=\pi(4x^2)\times (-3x+4)\\&=(4\pi x^2)\times (-3x+4)\\&=-12\pi x^3+16\pi x^2\\ &\approx -37{,}7x^3+50{,}27x^2\end{align}||
-
Interpréter la réponse
L’expression algébrique du volume du cylindre est |-12\pi x^3+16\pi x^2| ou environ |-37{,}7x^3+50{,}27x^2.|
L’exemple ci-dessous présente un problème où il faut traduire mathématiquement les informations de l'énoncé pour déterminer les expressions algébriques.
Dans le but de conserver les mêmes proportions pour les contenants de bonbons en forme de cône, les marchands tiennent à ce que la hauteur mesure trois unités de plus que le quadruple de la mesure du rayon.
Avec ces informations, détermine l'expression algébrique associée au volume de ces contenants.
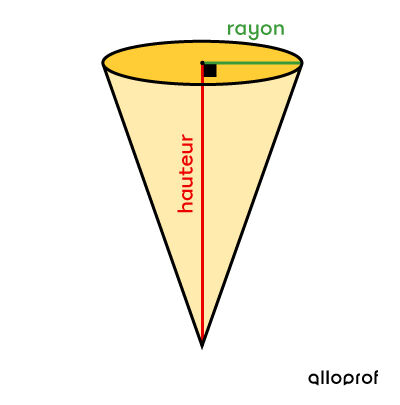
1. Représenter la situation par un dessin, au besoin
-
Identifier les expressions algébriques
À l'aide de la mise en situation, on peut attribuer la variable |x| à l'une des deux dimensions, ici le rayon, et déduire l’autre dimension. Ainsi, on pose :
|\begin{align} \color{#3A9A38}{r} &= \color{#3A9A38}{x} \\ \color{#EC0000}{h} &= \color{#EC0000}{4x + 3}\end{align}|
On peut donc modifier la représentation du cône de la façon suivante :

-
Utiliser la formule appropriée et substituer les expressions algébriques ||\begin{align} V &= \dfrac{A_b \times \color{#EC0000}{h}}{3} \\\\ &=\dfrac{\pi \color{#3A9A38}{r}^2 \times \color{#EC0000}{h}}{3}\\\\ &= \frac{\pi \color{#3A9A38}{x}^2 \times (\color{#EC0000}{4x+3})}{3}\end{align}||
-
Simplifier l'expression algébrique ||\begin{align} V &= \dfrac{\pi \color{#3A9A38}{x}^2 \times (\color{#EC0000}{4x+3})}{3} \\\\ &= \dfrac{4\pi x^3 +3\pi x^2}{3} \\\\ &= \dfrac{4}{3}\pi x^3 + \pi x^2 \\\\ &\approx 4{,}19x^3 + 3{,}14x^2\end{align}||
-
Interpréter la réponse
L'expression algébrique exacte représentant le volume des contenants est : |\dfrac{4}{3}\pi x^3+\pi x^2.|
L'expression algébrique arrondie qui est associée au volume est : |4{,}19x^3 + 3{,}14x^2.|
Remarque: on aurait aussi pu décider de conserver la variable |r| pour le rayon. Dans ce cas, la hauteur aurait été de |4r +3.| La solution aurait été |\dfrac{4}{3}\pi r^3+\pi r^2.|
En associant des expressions algébriques et des variables aux différentes mesures, cela permet d'obtenir les dimensions de tous les solides qui respectent les contraintes énoncées au début du problème.
Avec un peu plus d'informations, on peut arriver à trouver la valeur numérique associée à la variable utilisée.
Parfois, il arrive qu'aucune des mesures ne soit connue. Dans ce cas, on peut utiliser des expressions algébriques pour définir les mesures manquantes. L'utilisation de l'algèbre a pour avantage de représenter plusieurs réponses possibles.
Quelle est l'expression algébrique associée à l'aire de la base d'une pyramide dont le volume est de |\dfrac{8}{3}x^2 - \dfrac{2}{3}x\ \text{cm}^3| et la hauteur de |4x\ \text{cm?}|
-
Identifier la formule
Dans ce cas, on utilise la formule du volume d'une pyramide. ||\phantom{\dfrac{8}{3}x^2 - \dfrac{2}{3}x}\color{#EC0000}{V} = \dfrac{A_b \times \color{#333FB1}{h}}{3}|| -
Remplacer les variables par les valeurs connues ||\begin{align} \color{#EC0000}{V} &= \dfrac{A_b \times \color{#333FB1}{h}}{3} \\\\ \color{#EC0000}{\dfrac{8}{3}x^2 - \dfrac{2}{3}x } &= \dfrac{A_b\times \color{#333FB1}{4x}}{3} \end{align}||
-
Simplifier et isoler la variable ||\begin{align} \color{#EC0000}{\dfrac{8}{3}x^2 - \dfrac{2}{3}x } &= \dfrac{A_b\times \color{#333FB1}{4x}}{3} \\\\ 8x^2 - 2x &= A_b\times \color{#333FB1}{4x} \\ \\ \dfrac{8x^2-2x}{4x}&=A_b\\ 2x-0,5&=A_b \end{align}||
-
Interpréter la réponse
L'expression algébrique associée à l'aire de la base est |2x -0,5.|
Il est possible qu’il y ait des problèmes où l’on doive utiliser la factorisation lors de la résolution. En voici un exemple.
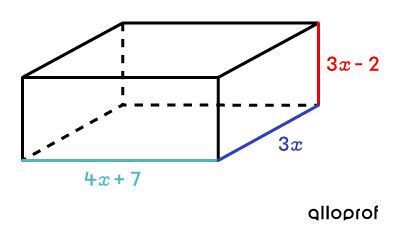
Quelle est l'expression algébrique associée à la mesure de chacune des dimensions d'un prisme à base rectangulaire dont le volume est |36 x^3 + 39x^2 - 42 x\ \text{cm}^3?|
-
Identifier la formule
Il n'y a pas assez d'informations sur les mesures du prisme pour utiliser la formule qui permet de calculer son volume. On effectue donc la factorisation du polynôme. -
Factorisation du polynôme ||\begin{align} &36x^3 + 39 x^2 - 42 x \\ =\ &3x (12x^2 + 13x - 14) && \text{mise en évidence simple} \\ =\ &3x (12x^2 +21x - 8x - 14) &&\text{Somme-produit}\\ =\ &3x \big(3x (4x+7) - 2(4x+7)\big) &&\\ =\ &\color{#333FB1}{3x} \color{#51B6C2}{(4x+7)} \color{#EC0000}{(3x-2)}\end{align}||
-
Interpréter la réponse
Puisque le calcul du volume d'un tel prisme consiste à multiplier 3 facteurs, on peut associer les expressions algébriques à chacune des dimensions du prisme :