The area of a solid can be expressed using algebraic expressions. When this happens, the measurements necessary to perform the calculations are expressed using monomials or polynomials. To solve this type of problem, a maximum of two variables are used to define the various measurements.
The area of a solid is the surface occupied by its faces. The area of a solid can be expressed using an algebraic expression if the measurement of its sides is expressed using variables or algebraic expressions. To calculate the area, use the area formulas corresponding to the solid. However, it is also possible to use the area formulas for the different figures corresponding to each of its faces.
At times, certain side measurements of a solid are missing. If so, they are replaced by variables or algebraic expressions. The algebraic expressions provided may be complete, or it may be necessary to translate the information in the statement mathematically to find them. A simplified algebraic expression is obtained by applying the area formulas.
The following example shows a problem where algebraic expressions are given.
Determine the algebraic expression associated with the lateral area of the square pyramid below.

-
Identify algebraic expressions
Since it is a square pyramid, use the formula |A_L=\dfrac{P_b\times a}{2}.|

-
Use the appropriate formula and substitute the algebraic expressions
||\begin{align} A_L&=\dfrac{\color{#333FB1}{P_b}\times \color{#EC0000}{a}}{2}\\ &=\dfrac{{\color{#333FB1}{4c}}\times \color{#EC0000}{4}}{2}\\ &=\dfrac{\color{#333FB1}{4(-2x+3)\times \color{#EC0000}{4}}}{2}\end{align}|| -
Simplify the algebraic expression
||\begin{align} A_L &= \dfrac{{\color{#333FB1}{4(-2x+3)}}\times \color{#EC0000}{4}}{2} \\ &= \dfrac{\color{#333FB1}{(-8x+12)}\times\cancelto{2}{\color{#EC0000}{4}}}{\cancel{2}}\\ &=(-8x+12)\times2\\ &=-16x+24\end{align}|| -
Interpret the answer
The algebraic expression for the total area of the pyramid is |-16x+24.|
The following example presents a problem where it is necessary to mathematically translate the information in the statement to determine the algebraic expressions.
To minimize the production costs of boxes used for transporting goods, the department’s engineers know that the boxes, which are rectangular prisms, must have a height of 5 units and their length must measure 2 units less than 3 times their width.
Based on this information, determine the algebraic expression associated with the total area of a box.
-
If possible, represent the situation with a drawing
-
Identify algebraic expressions
Using the information provided, assign the variable to one of the dimensions (i.e., the depth), and determine the other dimensions.|\begin{align}\color{#EC0000}{h} &= \color{#EC0000}{5}\\\color{#333FB1}{p} &= \color{#333FB1}{x}\\\color{#3A9A38}{l} &= \color{#3A9A38}{3x - 2}\end{align}|
Thus, we obtain the following illustration:
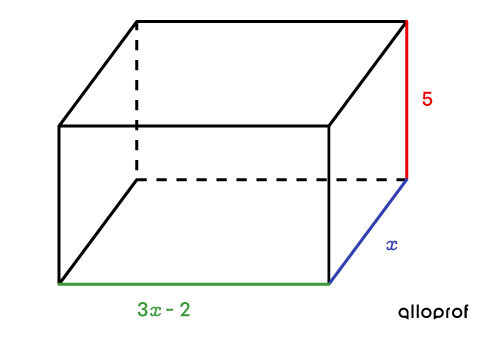
-
Use the appropriate formula and substitute the algebraic expressions
||\begin{align} A_T &= 2 \times A_b &&+&& A_L \\&= 2 \times \color{#3A9A38}{l} \times \color{#333FB1}{w} &&+&& P_b \times \color{#EC0000}{h}\\&=2 \times (\color{#3A9A38}{3x-2}) \times \color{#333FB1}{x} &&+&& (\color{#3A9A38}{3x - 2} + \color{#3A9A38}{3x - 2} + \color{#333FB1}{x} + \color{#333FB1}{x}) \times \color{#EC0000}{5}\end{align}|| -
Simplify the algebraic expression
||\begin{align} A_T &= 2 \times (\color{#3A9A38}{3x-2}) \times \color{#333FB1}{x}&&+&& (\color{#3A9A38}{3x - 2} + \color{#3A9A38}{3x - 2} + \color{#333FB1}{x} + \color{#333FB1}{x}) \times \color{#EC0000}{5}\\&= 2\times (3x^2 - 2x) &&+&& (8x - 4)\times \color{#EC0000}{5} \\&= 6x^2 - 4x &&+&& 40x - 20\\&= 6x^2 + 36x -20 \end{align}|| -
Interpret the answer
The algebraic expression for the total area of the prism is |6x^2 + 36x - 20.|
Using algebraic expressions to represent the measurement of the edges makes it possible to generalize and solve a larger number of problems. This method can also be applied with the concept of volume.
Sometimes, the measurements of a solid are not known. In this case, algebraic expressions can be used to define the missing measurements. The advantage of using algebra is that it will present all possible answers.
What is the algebraic expression associated with the measurement of one side of the prism’s base, knowing that the lateral area is |\color{#3A9A38}{80x^2}|?
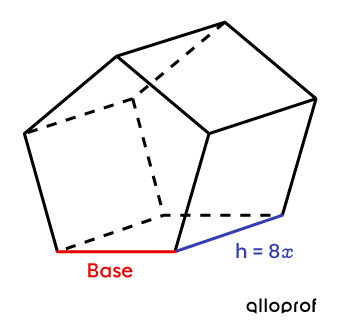
-
Use the appropriate formula
Use the formula for the lateral area of a prism.
||A_L=P_b\times h|| -
Replace the known values
||\begin{align} \color{#3A9A38}{A_L} &= \color{#EC0000}{P_b} \times \color{#333FB1}{h}\\ \color{#3A9A38}{80 x^2} &=\color{#EC0000}{P_b} \times \color{#333FB1}{8x}\end{align}|| -
Find the expression that represents the perimeter of the base
||\begin{align}80x^2&=P_b\times 8x\\\dfrac{80x^2}{\color{#EC0000}{8x}}&=\dfrac{P_b\times 8x}{\color{#EC0000}{8x}}\\10x&=P_b\end{align}|| -
Determine the measurement of the side of the base using the formula for perimeter
||\begin{align} P_b &= c+c+c+c+c \\ 10x &= 5c \\ \dfrac{10x}{\color{#EC0000}{5}} &= \dfrac{5c}{\color{#EC0000}{5}} \\ 2x &= c \end{align}|| -
Interpret the answer
The algebraic expression associated with the base of the prism is |2x.|
What is the algebraic expression associated with the height of a cylinder with a total area of |48\pi x^2| and the radius of the base is |3x|?
-
Use the appropriate formula
Use the formula for the total area of a cylinder.
||A_T = 2A_b + A_L|| -
Find the expression that represents the area of a base
||\begin{align} \color{#333FB1}{A_b} &= \pi r^2\\&=\pi (3x)^2\\&=\pi \times 9x^2 \\ &= \color{#333FB1}{9\pi x^2} \end{align}|| -
Replace the known values
||\begin{align} \color{#3A9A38}{A_t} &= 2\color{#333FB1}{A_b} + A_L\\ \color{#3A9A38}{48\pi x^2} &= 2\times \color{#333FB1}{9\pi x^2} + A_L \end{align}|| -
Find the expression that represents the lateral area
||\begin{align} 48\pi x^2&=18\pi x^2+A_L \\ 30\pi x^2&=A_L \end{align}|| -
Determine the height using the lateral area formula
||\begin{align} A_L &= P_b\times h \\ A_L &= 2\pi r \times h\\30\pi x^2 &= 2\pi(3x)\times h\\30\pi x^2&=6\pi x \times h\\ \dfrac{30\pi x^2}{\color{#EC0000}{6\pi x}} &= \dfrac{6\pi x \times h}{\color{#EC0000}{6\pi x}} \\ 5x &= h\end{align}|| -
Interpret the answer
The algebraic expression associated with the height of the cylinder is |5x.|