Pour trouver le ou les point(s) de rencontre entre une droite et une conique, on résout le système d’équations composé d’une équation de degré 1 et d’une équation de degré 2.
-
Utiliser la méthode de substitution afin d'obtenir une équation à une variable.
-
Exprimer l’équation de sorte qu’elle soit égale à |0.|
-
Résoudre l’équation pour trouver la ou les valeur(s) de la variable isolée.
-
Remplacer la ou les valeur(s) obtenue(s) dans l’une des équations de départ pour obtenir la ou les valeur(s) de l’autre variable.
-
Écrire les coordonnées du ou des point(s) d’intersection.
Contrairement à l'intersection entre une parabole et une conique, il y a 3 cas possibles quant au nombre de solutions :
-
la droite et la conique ne se croisent pas;
-
la droite et la conique ne se croisent qu’à un endroit, qu’on nomme point de tangence;
-
la droite et la conique se croisent en 2 endroits distincts.
Dans l'animation interactive qui suit, on peut sélectionner une conique, puis déplacer le curseur afin d’analyser les cas possibles.
-
Utiliser la méthode de substitution
On utilise la méthode de substitution puisque la variable |y,| dans l’équation de la droite, est déjà isolée.||\begin{align}
x^2+\color{#3a9a38}{y}^2&=10\\
x^2+(\color{#3a9a38}{2x+5})^2&=10
\end{align}|| -
Exprimer l’équation de sorte qu’elle soit égale à |0|
||\begin{align}
x^2+(2x+5)^2&=10\\
x^2+(4x^2+20x+25)&=10\\
\color{#3B87CD}{5}x^2+\color{#3A9A38}{20}x+\color{#EC0000}{15}&=0
\end{align}|| -
Résoudre l’équation
En utilisant la formule quadratique, on obtient :||\begin{align}
x&=\dfrac{-\color{#3A9A38}{b}\pm\sqrt{\color{#3A9A38}{b}^2-4\color{#3B87CD}{a}\color{#EC0000}{c}}}{2\color{#3B87CD}{a}}\\\\
&=\dfrac{-(\color{#3A9A38}{20})\pm\sqrt{(\color{#3A9A38}{20})^2-4(\color{#3B87CD}{5})(\color{#EC0000}{15})}}{2(\color{#3B87CD}{5})}\\\\
&=\dfrac{-20\pm\sqrt{100}}{10}\\\\
x_{\small{A}}&=-3\\
x_{\small{B}}&=-1
\end{align}|| -
Remplacer les valeurs obtenues dans l’une des équations de départ
Pour le point |A| en |x_{\small{A}}=-3,| on a :||\begin{align}
y_{\small{A}}&=2\color{#3A9A38}{x_{\small{A}}}+5\\
&=2(\color{#3A9A38}{-3})+5\\
&=-1
\end{align}||Quant au point |B| en |x_{\small{B}}=-1,| on a :||\begin{align}
y_{\small{B}}&=2\color{#3A9A38}{x_{\small{B}}}+5\\
&=2(\color{#3A9A38}{-1})+5\\
&=3
\end{align}|| -
Écrire les coordonnées des points d’intersection
Les coordonnées des 2 points d’intersection entre la droite |y=2x+5| et le cercle |x^2+y^2=10| sont |A(-3,-1)| et |B(-1,3).|

-
Utiliser la méthode de substitution
On utilise la méthode de substitution puisque la variable |y,| dans l’équation de la droite, est déjà isolée.||\begin{align}\dfrac{x^2}{36}+\dfrac{\color{#3a9a38}{y}^2}{49}&=1\\\\ \dfrac{x^2}{36}+\dfrac{(\color{#3a9a38}{-2x+6})^2}{49}&=1\end{align}|| -
Exprimer l’équation de sorte qu’elle soit égale à |0|
||\begin{align}\dfrac{x^2}{36}+\dfrac{(-2x+6)^2}{49}&=1\\\\ \dfrac{49x^2}{1\ 764}+\dfrac{36(-2x+6)^2}{1\ 764}&=1\\\\ \dfrac{49x^2+36(4x^2-24x+36)}{1\ 764}&=1\\\\ 49x^2+144x^2-864x+1\ 296&=1\ 764\\ \color{#3B87CD}{193}x^2\color{#3A9A38}{-864}x\color{#EC0000}{-468}=0\end{align}|| -
Résoudre l’équation
En utilisant la formule quadratique, on obtient : ||\begin{align}x&=\dfrac{-\color{#3A9A38}{b}\pm\sqrt{\color{#3A9A38}{b}^2-4\color{#3B87CD}{a}\color{#EC0000}{c}}}{2\color{#3B87CD}{a}}\\\\ &=\dfrac{-(\color{#3A9A38}{-864})\pm\sqrt{(\color{#3A9A38}{-864})^2-4(\color{#3B87CD}{193})(\color{#EC0000}{-468})}}{2(\color{#3B87CD}{193})}\\\\ &=\dfrac{864\pm\sqrt{1\ 107\ 792}}{386}\\\\ x_{\small{A}}&\approx-0{,}49\\ x_{\small{B}}&\approx4{,}97\end{align}|| -
Remplacer les valeurs obtenues dans l’une des équations de départ
Pour le point |A| en |x_{\small{A}}=-0{,}49,| on a : ||\begin{align}y_{\small{A}}&=-2\color{#3A9A38}{x_{\small{A}}}+6\\ &=-2(\color{#3A9A38}{-0{,}49})+6\\ &=6{,}98\end{align}||Quant au point |B| en |x_{\small{B}}=4{,}97,| on a : ||\begin{align}y_{\small{B}}&=-2\color{#3A9A38}{x_{\small{B}}}+6\\ &=-2(\color{#3A9A38}{4{,}97})+6\\ &=-3{,}94\end{align}|| -
Écrire les coordonnées des points d’intersection
Les coordonnées des 2 points d’intersection entre la droite |y=-2x+6| et l’ellipse |\dfrac{x^2}{36}+\dfrac{y^2}{49}=1| sont |A(-0{,}49;6{,}98)| et |B(4{,}97;-3{,}94).|

Détermine les coordonnées du ou des point(s) d’intersection entre la droite |y=2x-13| et l’hyperbole |\dfrac{x^2}{25}-\dfrac{y^2}{100}=1.|
-
Utiliser la méthode de substitution
On utilise la méthode de substitution puisque la variable |y,| dans l’équation de la droite, est déjà isolée.||\begin{align}\dfrac{x^2}{25}-\dfrac{\color{#3a9a38}{y}^2}{100}&=1\\\\ \dfrac{x^2}{25}-\dfrac{(\color{#3a9a38}{2x-13})^2}{100}&=1\end{align}|| -
Exprimer l’équation de sorte qu’elle soit égale à |0|
||\begin{align}\dfrac{x^2}{25}-\dfrac{(2x-13)^2}{100}&=1\\\\ \dfrac{4x^2-(2x-13)^2}{100}&=1\\\\ 4x^2-(4x^2-52x+169)&=100\\ 52x-269&=0\end{align}|| -
Résoudre l’équation ||\begin{align}52x-269&=0\\ 52x&=269\\ x_{\small{A}}&\approx5{,}17\end{align}||
-
Remplacer la valeur obtenue dans l’une des équations de départ
||\begin{align}y_{\small{A}}&=2\color{#3A9A38}{x_{\small{A}}}-13\\ &=2(\color{#3A9A38}{5{,}17})-13\\ &=-2{,}66\end{align}|| -
Écrire les coordonnées du point d’intersection
Les coordonnées du point d’intersection entre la droite |y=2x-13| et l’hyperbole |\dfrac{x^2}{25}-\dfrac{y^2}{100}=1| sont |A(5{,}17;-2{,}66).|

-
Utiliser la méthode de substitution
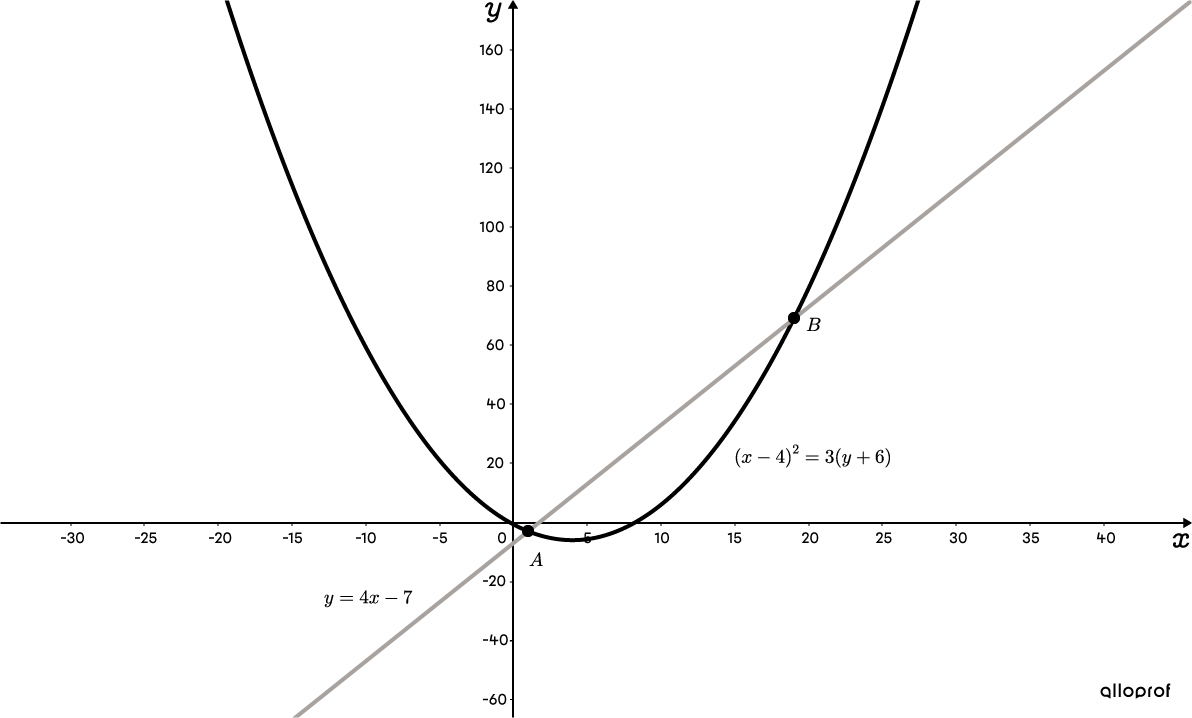
On utilise la méthode de substitution puisque la variable |y,| dans l’équation de la droite, est déjà isolée.||\begin{align}(x-4)^2&=3(\color{#3a9a38}{y}+6)\\ (x-4)^2&=3(\color{#3a9a38}{4x-7}+6)\\ (x-4)^2&=3(4x-1)\end{align}|| -
Exprimer l’équation de sorte qu’elle soit égale à |0|
||\begin{align}(x-4)^2&=3(4x-1)\\ x^2-8x+16&=12x-3\\ \color{#3B87CD}{1}x^2\color{#3A9A38}{-20}x+\color{#EC0000}{19}&=0\end{align}|| -
Résoudre l’équation
En utilisant la formule quadratique, on obtient : ||\begin{align}x&=\dfrac{-\color{#3A9A38}{b}\pm\sqrt{\color{#3A9A38}{b}^2-4\color{#3B87CD}{a}\color{#EC0000}{c}}}{2\color{#3B87CD}{a}}\\\\ &=\dfrac{-(\color{#3A9A38}{-20})\pm\sqrt{(\color{#3A9A38}{-20})^2-4(\color{#3B87CD}{1})(\color{#EC0000}{19})}}{2(\color{#3B87CD}{1})}\\\\ &=\dfrac{20\pm\sqrt{324}}{2}\\\\ x_{\small{A}}&=1\\ x_{\small{B}}&=19\end{align}|| -
Remplacer les valeurs obtenues dans l’une des équations de départ
Pour le point |A| en |x_{\small{A}}=1,| on a : ||\begin{align}y_{\small{A}}&=4\color{#3A9A38}{x_{\small{A}}}-7\\ &=4(\color{#3A9A38}{1})-7\\ &=-3\end{align}||Quant au point |B| en |x_{\small{B}}=19,| on a : ||\begin{align}y_{\small{B}}&=4\color{#3A9A38}{x_{\small{B}}}-7\\ &=4(\color{#3A9A38}{19})-7\\ &=69\end{align}|| -
Écrire les coordonnées des points d’intersection
Les coordonnées des 2 points d’intersection entre la droite |y=4x-7| et la parabole |(x-4)^2=3(y+6)| sont |A(1,-3)| et |B(19,69).|