Cette MiniRécup porte sur le rôle des paramètres |a,| |b,| |h| et |k| dans les fonctions dont la règle est sous forme canonique. Sa vidéo interactive, son résumé et son exercice récapitulatif te permettront de faire une courte révision à ce sujet.
Cette MiniRécup te permettra de bien comprendre le rôle des 4 paramètres utilisés dans l’équation d’une fonction sous forme canonique : les paramètres |a,| |b,| |h| et |k.|
Pour y arriver, tu dois être en mesure de travailler avec la règle de certaines fonctions, entre autres en changeant sa forme à l’aide d’une mise en évidence simple. Il est utile d’avoir une idée générale de la représentation graphique de certaines fonctions comme la fonction polynomiale de degré 2 ou la fonction partie entière, par exemple. Par contre, ce n’est pas nécessaire que tu les connaisses toutes. Finalement, tu dois savoir utiliser le plan cartésien.
L’identification des paramètres dans une règle
Voici un tableau qui présente la forme de base et la forme canonique de différentes fonctions.
| Forme de base | Forme canonique |
|---|---|
|
||f(x)=x^2|| |
||f(x)=\color{#3A9A38}a\big(\color{#EC0000}b(x-\color{#51B6C2}h)\big)^2+\color{#FA7921}k|| |
|
||f(x)=[x]|| |
||f(x)=\color{#3A9A38}a\big[\color{#EC0000}b(x-\color{#51B6C2}h)\big]+\color{#FA7921}k|| |
|
||f(x)=\sqrt x|| |
||f(x)=\color{#3A9A38}a\sqrt{\color{#EC0000}b(x-\color{#51B6C2}h)}+\color{#FA7921}k|| |
|
||f(x)=\cos x|| |
||f(x)=\color{#3A9A38}a\cos \big(\color{#EC0000}b(x-\color{#51B6C2}h)\big)+\color{#FA7921}k|| |
|
||f(x)=\vert x\vert || |
||f(x)=\color{#3A9A38}a\big\vert\color{#EC0000}b(x-\color{#51B6C2}h)\big\vert+\color{#FA7921}k|| |
Le rôle de chaque paramètre et l’effet sur le graphique
Le tableau suivant présente un résumé du rôle de chaque paramètre.
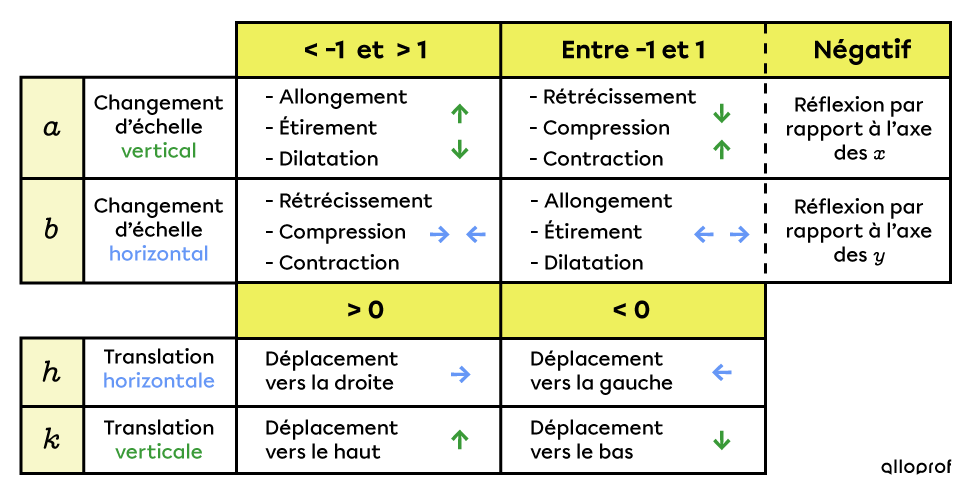
Le paramètre h est le nombre situé à droite du signe moins dans la parenthèse uniquement lorsque l’équation est sous forme canonique. Si l’équation n’est pas sous forme canonique, il faut effectuer une mise en évidence simple de |b.|
Exemple : |h(x)=2\vert 3x-12\vert | n’est pas sous forme canonique. En effectuant une mise en évidence simple, on obtient : ||\begin{align}h(x)&=2|3x-12|\\&=2|3(x\color{#EC0000}{-}\color{#51B6C2}{4})|\\\\&\Rightarrow\ \color{#51B6C2}{h}=\color{#51B6C2}{4}\end{align}||
Manipulation animée des paramètres
Dans l’animation suivante, il est possible de sélectionner la fonction de ton choix et de modifier les paramètres |a,| |b,| |h| et |k.| On peut voir apparaitre les modifications qui s’opèrent sur chaque fonction par rapport à celle de base. Pour la fonction exponentielle et logarithmique, on trouve un 5e paramètre (paramètre |c|) qu’il est aussi possible de modifier.
De la forme de base vers la forme canonique
La transformation qui associe un point de la forme de base d’une fonction à un point de sa forme canonique est la suivante. ||(x,y)\mapsto \left(\frac{x}{\color{#EC0000}b}+\color{#51B6C2}h,\color{#3A9A38}ay+\color{#FA7921}k\right)||
On peut donc prendre un point |(x,y)| de la forme de base et, en lui appliquant les paramètres de la forme canonique, obtenir son point associé appartenant à la fonction transformée.