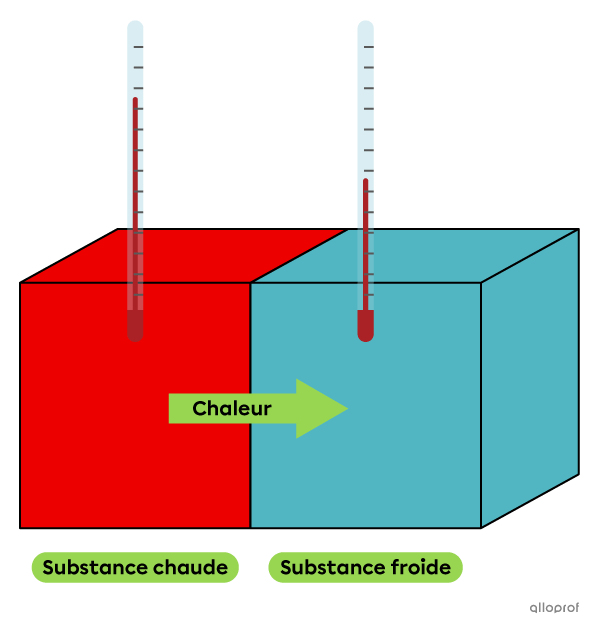
Lorsque deux substances de températures différentes sont en contact, une partie de l’énergie thermique de la substance la plus chaude se transfère à la substance la plus froide, jusqu’à ce que les deux substances atteignent la même température. Les deux substances subissent alors une variation de température. La substance chaude subit une diminution de température, car elle dégage de l’énergie thermique. La substance froide subit une augmentation de température, car elle absorbe de l’énergie thermique. Ce phénomène se nomme la chaleur.
La chaleur est le transfert d’énergie thermique entre deux systèmes de températures différentes.
La quantité de chaleur absorbée ou dégagée par un échantillon de substance dépend de la masse de l’échantillon, de la capacité thermique massique de la substance et de la variation de la température. On calcule la chaleur à l’aide de la formule suivante.
|Q=mc\Delta T|
où
|Q\ :| chaleur en joules |(\text{J})|
|m\ :| masse en grammes |(\text{g})|
|c\ :| capacité thermique massique en joules par gramme et par degré Celsius |(\text{J/g}{\cdot^\circ\!\text{C}})|
|\Delta T\ :| variation de la température en degrés Celsius |(^\circ\text{C})|
La quantité de chaleur |(Q)| est positive ou négative selon que la substance absorbe ou dégage de l'énergie thermique.
-
Lorsque |Q| est positive, cela signifie que la substance a absorbé de l’énergie thermique et que sa température a augmenté.
-
Lorsque |Q| est négative, cela signifie que la substance a dégagé de l’énergie thermique et que sa température a diminué.
La capacité thermique massique |(c)| est une propriété caractéristique. Elle correspond à la quantité d’énergie thermique nécessaire pour qu’un gramme d’une substance augmente sa température d'un degré Celsius. La capacité thermique massique se mesure en joules par gramme et par degré Celsius |(\text{J/g}{\cdot^\circ\!\text{C}}).| Le tableau suivant contient la capacité thermique massique de quelques substances.
|
Substance |
Air |
Aluminium |
Antigel |
Argent |
Cuivre |
Eau liquide |
Éthanol |
Fer |
Mercure |
Plomb |
Verre |
|---|---|---|---|---|---|---|---|---|---|---|---|
|
|c| |
|1{,}01| |
|0{,}90| |
|2{,}20| |
|0{,}24| |
|0{,}39| |
|4{,}19| |
|2{,}44| |
|0{,}45| |
|0{,}14| |
|0{,}13| |
|0{,}84| |
Source des données : Meziane et al., 2015[1] |
|||||||||||
En bref, la capacité thermique massique d’une substance décrit la capacité de celle-ci à faire varier sa température.
-
Plus la capacité thermique massique d’une substance est faible, plus il est facile pour cette substance d'augmenter ou de diminuer sa température. C’est le cas entre autres de l’argent, du mercure et du plomb.
-
Plus la capacité thermique massique d’une substance est élevée, plus il est difficile pour cette substance d’augmenter ou de diminuer sa température. C’est le cas entre autres de l’antigel, de l’eau liquide et de l’éthanol.
Pour connaitre la capacité thermique massique de plus de substances, consulte la fiche suivante.
La variation de la température d’une substance |(\Delta T)| est la différence entre sa température finale |(T_{\text{f}})| et sa température initiale |(T_{\text{i}}).|
|\Delta T=T_{\text{f}}-T_{\text{i}}|
où
|\Delta T\ :| variation de la température en degrés Celsius |(^\circ\text{C})|
|T_{\text{f}}\ :| température finale en degrés Celsius |(^\circ\text{C})|
|T_{\text{i}}\ :| température initiale en degrés Celsius |(^\circ\text{C})|
Quelle chaleur est absorbée par un cube de fer de |0{,}475\ \text{kg}| lorsque sa température varie de |10\ ^\circ\text{C}| à |22\ ^\circ\text{C}|?
La capacité thermique massique du fer est de |0{,}45\ \text{J/g}{\cdot^\circ\!\text{C}}.|
-
On identifie les données.
||\begin{align}Q &=\ ?\ \text{J}\\m &=0{,}475\ \cancel{\text{kg}}\times1\ 000\ \text{g/}\cancel{\text{kg}}= 475\ \text{g}\\c &=0{,}45\ \text{J/g}{\cdot^\circ\!\text{C}}\\T_{\text{f}} &=22\ ^\circ\text{C}\\T_{\text{i}} &=10\ ^\circ\text{C}\end{align}||
On calcule la variation de température à l’aide de la formule suivante.
||\begin{align}\Delta T &=T_{\text{f}}-T_{\text{i}}\\\Delta T &=22\ ^\circ\text{C}-10\ ^\circ\text{C}\\\Delta T &=12\ ^\circ\text{C}\end{align}|| -
On détermine la formule à utiliser.
||Q=mc\Delta T|| -
On remplace les variables et on résout l’équation.
||\begin{align}Q &=475\ \cancel{\text{g}}\ \times0{,}45\ \text{J/}\cancel{\text{g}\cdot^\circ\!\text{C}}\ \times12\ \cancel{^\circ\text{C}}\\Q &=2\ 565\ \text{J}\end{align}|| -
On répond à la question.
Le cube de fer a absorbé |2\ 565\ \text{J}| ou environ |2{,}6\ \text{kJ}| en tenant compte des chiffres significatifs.
Quelle masse d’eau dégage |1\ 100\ \text{J}| d’énergie thermique si sa température varie de |39{,}0\ ^\circ\text{C}| à |20{,}5\ ^\circ\text{C}|?
La capacité thermique massique de l’eau est de |4{,}19\ \text{J/g}{\cdot^\circ\!\text{C}}.|
-
On identifie les données. Puisque la température de l’eau a diminué, on sait que l’eau a dégagé de l’énergie thermique et que la valeur de |Q| est négative.
||\begin{align}Q &=-1\ 100\ \text{J}\\m &=\ ?\ \text{g}\\c &=4{,}19\ \text{J/g}{\cdot^\circ\!\text{C}}\\T_{\text{f}} &=20{,}5\ ^\circ\text{C}\\T_{\text{i}} &=39{,}0\ ^\circ\text{C}\end{align}||
On calcule la variation de la température à l’aide de la formule suivante.
||\begin{align}\Delta T &=T_{\text{f}}-T_{\text{i}}\\\Delta T &=20{,}5\ ^\circ\text{C}-39{,}0\ ^\circ\text{C}\\\Delta T &=-18{,}5\ ^\circ\text{C}\end{align}|| -
On détermine la formule à utiliser et on isole |m.|
||Q=mc\Delta T\Rightarrow m=\dfrac{Q}{c\Delta T}|| -
On remplace les variables et on résout l’équation.
||\begin{align}m &=\dfrac{-1\ 100\ \cancel{\text{J}}}{4{,}19\ \cancel{\text{J}}\text{/g}\cancel{^\circ\!\text{C}}\ \times-18{,}5\ \cancel{^\circ\text{C}}}\\\\m &\approx14{,}2\ \text{g}\end{align}|| -
On répond à la question.
La masse de l’eau est d’environ |14{,}2\ \text{g}.|
En laboratoire, on transfère |260\ \text{J}| de chaleur à un bloc de |25\ \text{g}| d’un métal inconnu et on observe que sa température passe de |24\ ^\circ\text{C}| à |104\ ^\circ\text{C}.|
Détermine la capacité thermique massique de ce métal inconnu, puis identifie de quel métal il s’agit.
|
Métal |
Aluminium |
Argent |
Cuivre |
Fer |
Mercure |
Plomb |
|---|---|---|---|---|---|---|
|
|c| |
|0{,}90| |
|0{,}24| |
|0{,}39| |
|0{,}45| |
|0{,}14| |
|0{,}13| |
Source des données : Meziane et al., 2015[1] |
||||||
-
On identifie les données.
||\begin{align}Q &=260\ \text{J}\\c &=\ ?\ \text{J/g}{\cdot^\circ\!\text{C}}\\m &=25\ \text{g}\\T_{\text{f}} &=104\ ^\circ\text{C}\\T_{\text{i}} &=24\ ^\circ\text{C}\end{align}||
On calcule la variation de la température à l’aide de la formule suivante.
||\begin{align}\Delta T &=T_{\text{f}}-T_{\text{i}}\\\Delta T &=104\ ^\circ\text{C}-24\ ^\circ\text{C}\\\Delta T &=80\ ^\circ\text{C}\end{align}|| -
On détermine la formule à utiliser et on isole |c.|
||\begin{align}Q=mc\Delta T \Rightarrow c=\dfrac{Q}{m\Delta T}\end{align}|| -
On remplace les variables et on résout l’équation.
||\begin{align}c &=\dfrac{260\ \text{J}}{25\ \text{g}\times80\ ^\circ\text{C}}\\\\c &=0{,}13\ \text{J/g}{\cdot^\circ\!\text{C}}\end{align}|| -
On répond à la question.
La capacité thermique massique du métal inconnu est de |0{,}13\ \text{J/g}{\cdot^\circ\!\text{C}}.| Il s'agit donc du plomb.
Un litre |(1\ \text{L})| d’antigel à |5{,}4\ ^\circ\text{C}| absorbe |10\ 500\ \text{J}| d’énergie thermique.
a) Quelle est la variation de la température de l'antigel?
b) Quelle est la température finale de l’antigel?
La masse volumique |(\rho)| de l’antigel est de |1{,}135\ \text{g/mL}.|
La capacité thermique massique de l’antigel est de |2{,}20\ \text{J/g}{\cdot^\circ\!\text{C}}.|
a) Déterminer la variation de la température de l’antigel.
-
On identifie les données. Puisque l’antigel a absorbé de l’énergie thermique, on sait que la valeur de |Q| est positive.
||\begin{align}Q &=10\ 500\ \text{J}\\c &=2{,}20\ \text{J/g}{\cdot^\circ\!\text{C}}\\m &=\ ?\ \text{g}\\\Delta T &=\ ?\ ^\circ\text{C}\end{align}||
Sachant que |1\ \text{L}| d’antigel correspond à |1\ 000\ \text{mL}| d’antigel, on calcule la masse de l’antigel à l’aide de la démarche suivante.
||\begin{align}\\\rho &=1{,}135\ \text{g/mL}&\\m &=\ ?\ \text{g}\\V &= 1\ 000\ \text{mL}\\\\\rho &=\dfrac{m}{V} \Rightarrow m=\rho\times V\\\\m &=1{,}135\ \text{g/}\cancel{\text{mL}}\times1\ 000\ \cancel{\text{mL}}\\m &=1\ 135\ \text{g}\end{align}|| -
On détermine la formule à utiliser et on isole |\Delta T.|
||Q=mc\Delta T\Rightarrow\Delta T=\dfrac{Q}{mc}|| -
On remplace les variables et on résout l’équation.
||\begin{align}\Delta T &=\dfrac{10\ 500\ \cancel{\text{J}}}{1\ 135\ \cancel{\text{g}}\times2{,}20\ \cancel{\text{J}}\text{/}\cancel{\text{g}}{\cdot^\circ\!\text{C}}}\\\\\Delta T &\approx4{,}21\ ^\circ\text{C}\end{align}|| -
On répond à la question.
La variation de la température de l’antigel est d’environ |4{,}21\ ^\circ\text{C}.|
b) Déterminer la température finale de l’antigel
-
On identifie les données.
||\begin{align}\Delta T &=4{,}21\ ^\circ\text{C}\\T_{\text{i}} &=5{,}4^\circ\text{C}\\T_{\text{f}} &=\ ?\ ^\circ\text{C}\end{align}|| -
On détermine la formule à utiliser et on isole |T_{\text{f}}.|
||\Delta T=T_{\text{f}}-T_{\text{i}} \Rightarrow T_{\text{f}}=\Delta T+T_{\text{i}}|| -
On remplace les variables et on résout l’équation.
||\begin{align}T_{\text{f}} &=4{,}21 ^\circ\text{C}+5{,}4 ^\circ\text{C}\\T_{\text{f}} &\approx9{,}6\ ^\circ\text{C}\end{align}|| -
On répond à la question.
La température finale de l’antigel est d’environ |9{,}6\ ^\circ\text{C}.|
En laboratoire, on plonge une bille d’aluminium de |78\ \text{g}| dont la température initiale est de |280\ ^\circ\text{C}| dans |350\ \text{mL}| d’eau. Après quelques minutes, la température de l’eau se stabilise à |28\ ^\circ\text{C}.| Détermine la température initiale de l’eau.
La capacité thermique massique de l’aluminium est de |0{,}90\ \text{J/g}{\cdot^\circ\!\text{C}}| et celle de l’eau est de |4{,}19\ \text{J/g}{\cdot^\circ\!\text{C}}.|
La masse volumique de l’eau est de |1{,}00\ \text{g/mL}.|
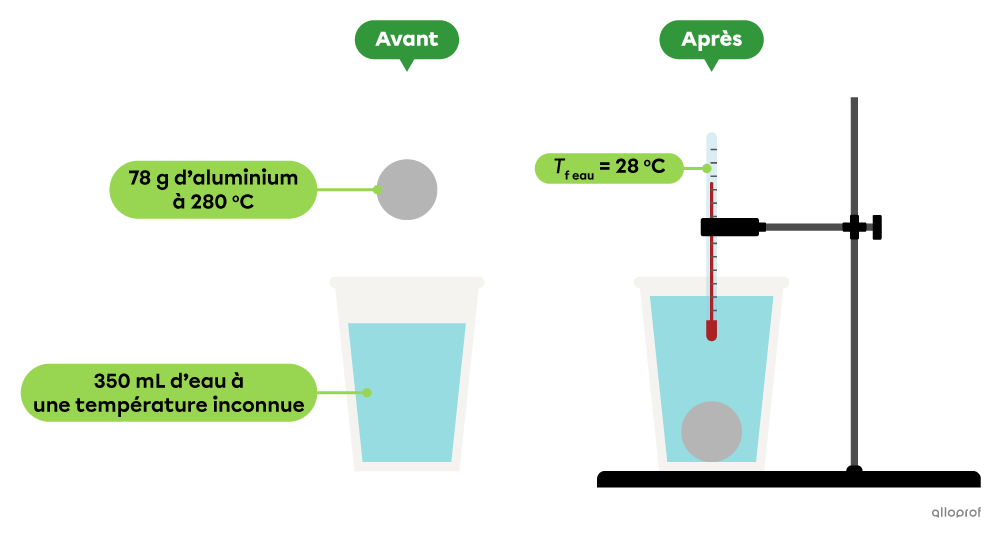
Dans cet exemple, on considère que toute l’énergie dégagée par la bille d’aluminium a été absorbée par l’eau sans aucune perte d’énergie dans l’air ambiant. La température finale de l’eau est aussi la température finale de la bille d'aluminium.
On calcule la chaleur dégagée par la bille d’aluminium.
-
On identifie les données.
||\begin{align}Q_{\text{aluminium}} &=\ ?\ \text{J}\\m_{\text{aluminium}} &=78\ \text{g}\\c_{\text{aluminium}} &=0{,}90\ \text{J/g}{\cdot^\circ\!\text{C}}\\\Delta T_{\text{aluminium}} &=T_{\text{f}}-T_{\text{i}}\\\Delta T_{\text{aluminium}} &=28\ ^\circ\text{C}-280\ ^\circ\text{C}=-252\ ^\circ\text{C}\end{align}|| -
On détermine la formule à utiliser.
||Q=mc\Delta T|| -
On remplace les variables et on résout l’équation.
||\begin{align}Q &=78\ \cancel{\text{g}}\ \times0{,}90\ \text{J/}\cancel{\text{g}\cdot^\circ\!\text{C}}\ \times-252\ \cancel{^\circ\text{C}}\\Q &=-17\ 690{,}4\ \text{J}\end{align}||
On peut dire que la bille d’aluminium a dégagé |17\ 690{,}4\ \text{J}| de chaleur et que l’eau a absorbé |17\ 690{,}4\ \text{J}| de chaleur. On peut maintenant calculer la température initiale de l’eau à l’aide de la démarche suivante.
-
On identifie les données.
||\begin{align}Q_{eau} &=-17\ 690{,}4\ \text{J}\\c_{eau} &=4{,}19\ \text{J/g}{\cdot^\circ\!\text{C}}\\m_{\text{eau}} &=\ ?\ \text{g}\\\Delta T_{eau} &=\ ?\ ^\circ\text{C}\end{align}||
On calcule la masse de l’eau à l’aide de la démarche suivante.
||\begin{align}\rho=\dfrac{m}{V} \Rightarrow m &=\rho\times V\\m &=1{,}00\ \text{g/}\cancel{\text{mL}}\times350\ \cancel{\text{mL}}\\m &=350\ \text{g}\end{align}|| -
On détermine la formule à utiliser et on isole |\Delta T.|
||Q=mc\Delta T\Rightarrow\Delta T=\dfrac{Q}{mc}|| -
On remplace les variables et on résout l'équation.
||\begin{align}\Delta T &=\dfrac{17\ 690{,}4\ \cancel{\text{J}}}{350\ \cancel{\text{g}}\times4{,}19\ \cancel{\text{J}}\text{/}\cancel{\text{g}}{\cdot^\circ\!\text{C}}}\\\\\Delta T &\approx12{,}1\ ^\circ\text{C}\end{align}|| -
À partir de la formule de la variation de la température, on isole |T_{\text{i}}| et on calcule la température initiale de l’eau.
||\begin{align}\Delta T=T_{\text{f}}-T_{\text{i}} \Rightarrow T_{\text{i}} &=T_{\text{f}}-\Delta T\\T_{\text{i}} &=28\ ^\circ\text{C}-12{,}1\ ^\circ\text{C}\\T_{\text{i}} &\approx16\ ^\circ\text{C} \end{align}|| -
On répond à la question.
La température initiale de l’eau était d’environ |16\ ^\circ\text{C}.|
Pour valider ta compréhension à propos de l'énergie thermique de façon interactive, consulte la MiniRécup suivante :

-
Meziane. M et all. (2015) Delta - Chimie. Chenelière Éducation.