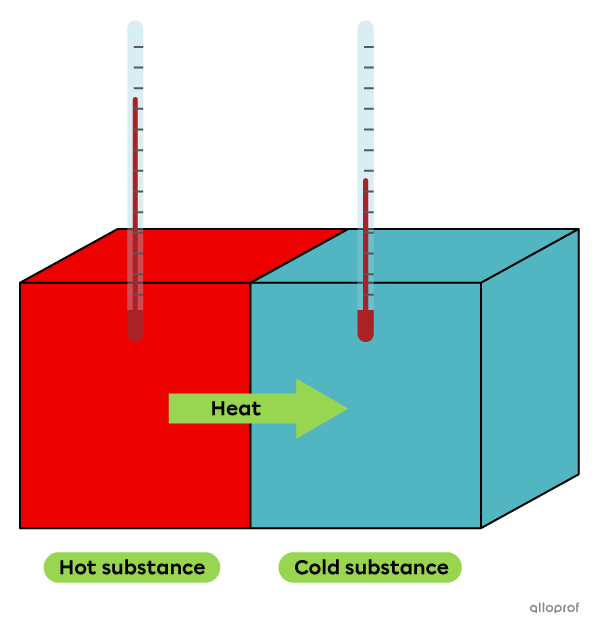
When two substances of different temperatures are in contact, some of the thermal energy of the hotter substance is transferred to the colder substance, until the two substances reach the same temperature. Both substances then undergo a temperature change. The hot substance experiences a decrease in temperature because it releases thermal energy. The cold substance experiences an increase in temperature because it absorbs thermal energy. This phenomenon is called heat.
Heat is the transfer of thermal energy between two systems at different temperatures.
The amount of heat absorbed or released by a substance depends on the mass of the substance, the specific heat capacity of the substance and the temperature change. Heat is calculated using the following formula.
|Q=mc\Delta T|
where
|Q\!:| heat in joules |(\text{J})|
|m\!:| mass in grams |(\text{g})|
|c\!:| specific heat capacity in joules per gram and degrees Celsius |(\text{J/g}{\cdot^\circ\!\text{C}})|
|\Delta T\!:| temperature change in degrees Celsius |(^\circ\text{C})|
The amount of heat |(Q)| is positive or negative depending on whether the substance absorbs or releases thermal energy.
-
When |Q| is positive, the substance absorbs thermal energy and its temperature increases.
-
When |Q| is negative, the substance releases thermal energy and its temperature decreases.
The specific heat capacity |(c)| is a characteristic property. It is the amount of thermal energy required to raise the temperature of one gram of a substance by one degree Celsius. The specific heat capacity is measured in joules per gram and degrees Celsius |(\text{J/g}{\cdot^\circ\!\text{C}}).| The following table gives the specific heat capacity of some substances.
|
Substance |
Air |
Aluminum |
Antifreeze |
Silver |
Copper |
Liquid water |
Ethanol |
Iron |
Mercury |
Lead |
Glass |
|---|---|---|---|---|---|---|---|---|---|---|---|
|
|\bf c| |
|1.01| |
|0.90| |
|2.20| |
|0.24| |
|0.39| |
|4.19| |
|2.44| |
|0.45| |
|0.14| |
|0.13| |
|0.84| |
Source: Couture et al., (2011)[1] |
|||||||||||
In short, the specific heat capacity of a substance describes its ability to change its temperature.
-
The lower the specific heat capacity of a substance, the easier it is for the substance to raise or lower its temperature. This is the case for silver, mercury and lead, among others.
-
The higher the specific heat capacity of a substance, the harder it is for that substance to raise or lower its temperature. Examples include antifreeze, liquid water and ethanol.
To find out the specific heat capacity of more substances, consult the following sheet.
The temperature change of a substance |(\Delta T)| is the difference between the final temperature |(T_{\text{f}})| and the initial temperature |(T_{\text{i}}).|
|\Delta T=T_{\text{f}}-T_{\text{i}}|
where
|\Delta T\!:| temperature change in degrees Celsius |(^\circ\text{C})|
|T_{\text{f}}\!:| final temperature in degrees Celsius |(^\circ\text{C})|
|T_{\text{i}}\!:| initial temperature in degrees Celsius |(^\circ\text{C})|
How much heat is absorbed by a |0.475\ \text{kg}| iron cube when its temperature changes from |10^\circ\text{C}| to |22^\circ\text{C}|?
The specific heat capacity of iron is |0.45\ \text{J/g}{\cdot^\circ\!\text{C}}.|
-
First, identify the given values: ||\begin{align}Q &=\ ?\ \text{J}\\m &=0.475\ \cancel{\text{kg}}\times1000\ \text{g/}\cancel{\text{kg}}= 475\ \text{g}\\c &=0.45\ \text{J/g}{\cdot^\circ\!\text{C}}\\T_{\text{f}} &=22^\circ\text{C}\\T_{\text{i}} &=10^\circ\text{C}\end{align}||
The temperature change is calculated using the following formula: ||\begin{align}\Delta T &=T_{\text{f}}-T_{\text{i}}\\\Delta T &=22^\circ\text{C}-10^\circ\text{C}\\\Delta T &=12^\circ\text{C}\end{align}|| -
Choose and write down the relevant formula: ||Q=mc\Delta T||
-
Replace the variables by the known values and solve the problem: ||\begin{align}Q &=475\ \cancel{\text{g}}\ \times0.45\ \text{J/}\cancel{\text{g}}{\cdot^\circ\!\text{C}}\ \times12\ \cancel{^\circ\text{C}}\\Q &=2565\ \text{J}\end{align}||
-
The final answer is:
An iron cube absorbed |2565\ \text{J},| or approximately |2.6\ \text{kJ}| when taking significant figures into account.
What mass of water releases |1100\ \text{J}| of thermal energy if its temperature decreases from |39.0^\circ\text{C}| to |20.5^\circ\text{C}|?
The specific heat capacity of water is |4.19\ \text{J/g}{\cdot^\circ\!\text{C}}.|
-
First, identify the given values. Since the water temperature decreased, the water released thermal energy and the value of |Q| is negative. ||\begin{align}Q &=-1100\ \text{J}\\m &=\ ?\ \text{g}\\c &=4.19\ \text{J/g}{\cdot^\circ\!\text{C}}\\T_{\text{f}} &=20.5^\circ\text{C}\\T_{\text{i}} &=39.0^\circ\text{C}\end{align}||The temperature change is calculated using the following formula: ||\begin{align}\Delta T &=T_{\text{f}}-T_{\text{i}}\\\Delta T &=20.5^\circ\text{C}-39.0^\circ\text{C}\\\Delta T &=-18.5^\circ\text{C}\end{align}||
-
Choose and write down the formula where |m| is isolated: ||Q=mc\Delta T\Rightarrow m=\dfrac{Q}{c\Delta T}||
-
Replace the variables by the known values and solve the problem:
||\begin{align}m &=\dfrac{-1100\ \cancel{\text{J}}}{4.19\ \cancel{\text{J}}\text{/g}\cancel{^\circ\!\text{C}}\ \times-18.5\ \cancel{^\circ\text{C}}}\\\\m &\approx14.2\ \text{g}\end{align}|| -
The final answer is:
The mass of water is approximately |14.2\ \text{g}.|
In a lab, |260\ \text{J}| of heat is transferred to a |25\ \text{g}| block of unknown metal. The temperature rises from |24^\circ\text{C}| to |104^\circ\text{C}.|
Determine the specific heat capacity of the metal in order to identify it.
|
Metal |
Aluminum |
Silver |
Copper |
Iron |
Mercury |
Lead |
|---|---|---|---|---|---|---|
|
|\bf c| |
|0.90| |
|0.24| |
|0.39| |
|0.45| |
|0.14| |
|0.13| |
Source: Couture et al., (2011)[1] |
||||||
-
First, identify the given values:
||\begin{align}Q &=260\ \text{J}\\c &=\ ?\ \text{J/g}{\cdot^\circ\!\text{C}}\\m &=25\ \text{g}\\T_{\text{f}} &=104^\circ\text{C}\\T_{\text{i}} &=24^\circ\text{C}\end{align}||
The temperature change is calculated using the following formula:
||\begin{align}\Delta T &=T_{\text{f}}-T_{\text{i}}\\\Delta T &=104^\circ\text{C}-24^\circ\text{C}\\\Delta T &=80^\circ\text{C}\end{align}|| -
Choose and write down the formula where |c| is isolated: ||\begin{align}Q=mc\Delta T \Rightarrow c=\dfrac{Q}{m\Delta T}\end{align}||
-
Replace the variables by the known values and solve the problem:
||\begin{align}c &=\dfrac{260\ \text{J}}{25\ \text{g}\times80^\circ\text{C}}\\\\c &=0.13\ \text{J/g}{\cdot^\circ\!\text{C}}\end{align}|| -
The final answer is:
The specific heat capacity of the unknown metal is |0.13\ \text{J/g}{\cdot^\circ\!\text{C}},| which corresponds to lead.
One litre |(1\ \text{L})| of antifreeze at |5.4^\circ\text{C}| absorbs |10\ 500\ \text{J}| of thermal energy.
a) What is the temperature change of antifreeze?
b) What is the final temperature of antifreeze?
The density |(\rho)| of antifreeze is |1.135\ \text{g/mL}.|
The specific heat capacity of antifreeze is |2.20\ \text{J/g}{\cdot^\circ\!\text{C}}.|
a) Determine the temperature change of antifreeze.
-
First, identify the given values. Since the antifreeze absorbed thermal energy, the value of |Q| is positive. ||\begin{align}Q &=10\ 500\ \text{J}\\c &=2.20\ \text{J/g}{\cdot^\circ\!\text{C}}\\m &=\ ?\ \text{g}\\\Delta T &=\ ?^\circ\text{C}\end{align}||
Knowing that |1\ \text{L}| of antifreeze corresponds to |1\ 000\ \text{mL},| the mass of the antifreeze can be calculated using the following procedure: ||\begin{align}\\\rho &=1.135\ \text{g/mL}&\\m &=\ ?\ \text{g}\\V &= 1\ 000\ \text{mL}\\\\\rho &=\dfrac{m}{V} \Rightarrow m=\rho\times V\\\\m &=1.135\ \text{g/}\cancel{\text{mL}}\times1\ 000\ \cancel{\text{mL}}\\m &=1\ 135\ \text{g}\end{align}|| -
Choose and write down the formula where |\Delta T| is isolated: ||Q=mc\Delta T\Rightarrow\Delta T=\dfrac{Q}{mc}||
-
Replace the variables by the known values and solve the problem: ||\begin{align}\Delta T &=\dfrac{10\ 500\ \cancel{\text{J}}}{1\ 135\ \cancel{\text{g}}\times2.20\ \cancel{\text{J}}\text{/}\cancel{\text{g}}{\cdot^\circ\!\text{C}}}\\\\\Delta T &\approx4.21^\circ\text{C}\end{align}||
-
The answer is:
The temperature of antifreeze changed approximately by |4.21^\circ\text{C}.|
b) Determine the final temperature of antifreeze.
-
First, identify the given values.
||\begin{align}\Delta T &=4.21^\circ\text{C}\\T_{\text{i}} &=5.4^\circ\text{C}\\T_{\text{f}} &=\ ?^\circ\text{C}\end{align}||
-
Choose and write down the formula where |T_{\text{f}}| is isolated: ||\Delta T=T_{\text{f}}-T_{\text{i}} \Rightarrow T_{\text{f}}=\Delta T+T_{\text{i}}||
-
Replace the variables by the known values and solve the problem:
||\begin{align}T_{\text{f}} &=4.21 ^\circ\text{C}+5.4 ^\circ\text{C}\\T_{\text{f}} &\approx9.6^\circ\text{C}\end{align}||
-
The answer is:
The final temperature of antifreeze is approximately |9.6^\circ\text{C}.|
In a lab, a |78\ \text{g}| aluminum ball with an initial temperature of |280^\circ\text{C}| is placed in |350\ \text{mL}| of water. After a few minutes, the water temperature reaches and stays at |28^\circ\text{C}.| Determine the initial temperature of the water.
The specific heat capacity of aluminum is |0.90\ \text{J/g}{\cdot^\circ\!\text{C}}| and of water is |4.19\ \text{J/g}{\cdot^\circ\!\text{C}}.|
The density of water is |1.00\ \text{g/mL}.|
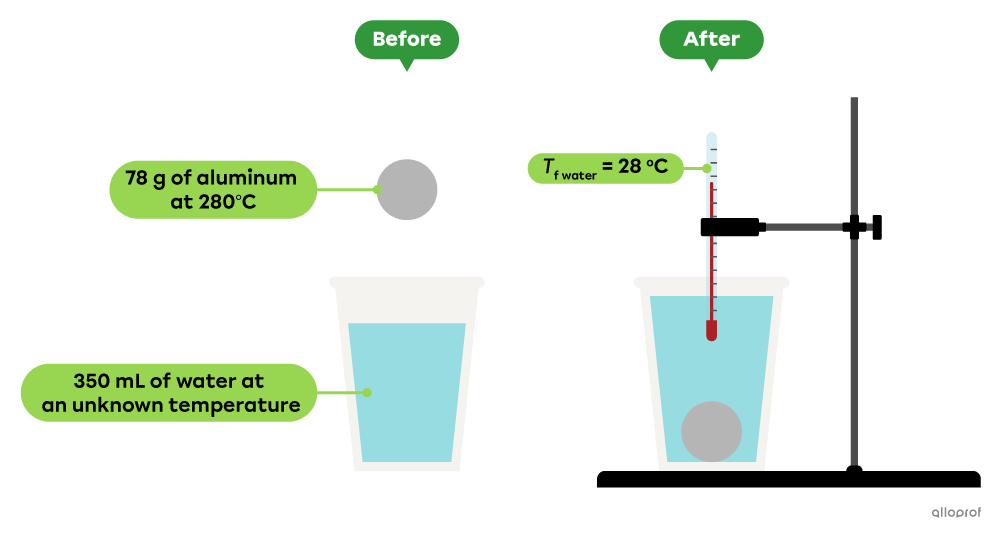
In this example, it is assumed that all the energy released by the aluminum ball is absorbed by the water, with no loss of energy to the surrounding air. The final temperature of the water is also the final temperature of the aluminum ball.
Let’s calculate the heat released by the aluminum ball.
-
First, identify the given values.
||\begin{align}Q_{\text{aluminum}} &=\ ?\ \text{J}\\m_{\text{aluminum}} &=78\ \text{g}\\c_{\text{aluminum}} &=0.90\ \text{J/g}{\cdot^\circ\!\text{C}}\\\Delta T_{\text{aluminum}} &=T_{\text{f}}-T_{\text{i}}\\\Delta T_{\text{aluminum}} &=28^\circ\text{C}-280^\circ\text{C}=-252^\circ\text{C}\end{align}||
-
Choose and write down the formula: ||Q=mc\Delta T||
-
Replace the variables by the known values and solve the problem:
||\begin{align}Q &=78\cancel{\text{g}}\ \times0.90\ \text{J/}\cancel{\text{g}}{\cdot^\circ\!\text{C}}\ \times-252\cancel{^\circ\text{C}}\\Q &=-17\ 690.4\ \text{J}\end{align}||
The aluminum ball releases |17\ 690.4\ \text{J}| of heat and the water absorbs |17\ 690.4\ \text{J}| of heat. Now, let’s calculate the initial temperature of the water.
-
First, identify the given values.
||\begin{align}Q_{water} &=-17\ 690.4\ \text{J}\\c_{water} &=4.19\ \text{J/g}{\cdot^\circ\!\text{C}}\\m_{\text{water}} &=\ ?\ \text{g}\\\Delta T_{water} &=\ ?^\circ\text{C}\end{align}||
The mass of the water is calculated using the following procedure. ||\begin{align}\rho=\dfrac{m}{V} \Rightarrow m &=\rho\times V\\m &=1.00\ \text{g/}\cancel{\text{mL}}\times350\ \cancel{\text{mL}}\\m &=350\ \text{g}\end{align}|| -
Choose and write down the formula where |\Delta T| is isolated: ||Q=mc\Delta T\Rightarrow\Delta T=\dfrac{Q}{mc}||
-
Replace the variables by the known values and solve the problem: ||\begin{align}\Delta T &=\dfrac{17\ 690.4\ \cancel{\text{J}}}{350\ \cancel{\text{g}}\times4.19\ \cancel{\text{J}}\text{/}\cancel{\text{g}}\cdot^\circ\!\text{C}}\\\\\Delta T &\approx12.1^\circ\text{C}\end{align}||
-
Using the temperature change formula, isolate the |T_{\text{i}}| and calculate the initial temperature:
||\begin{align}\Delta T=T_{\text{f}}-T_{\text{i}} \Rightarrow T_{\text{i}} &=T_{\text{f}}-\Delta T\\T_{\text{i}} &=28^\circ\text{C}-12.1^\circ\text{C}\\T_{\text{i}} &\approx16^\circ\text{C} \end{align}||
-
The final answer is:
The initial temperature of water is approximately |16^\circ\text{C}.|
Pour valider ta compréhension à propos de l'énergie thermique de façon interactive, consulte la MiniRécup suivante :

Couture, I., Lacombe-Harvey, M., & Levasseur-Thériault, G. (2011) Quantum - Chemistry. Chenelière Éducation.