Cette MiniRécup est une révision de plusieurs sujets de géométrie de 1re et de 2e secondaire. Pour bien comprendre les 2 vidéos, tu dois t’assurer de connaitre les éléments suivants : la différence entre le concept de périmètre et celui d’aire d’une figure plane, les formules de périmètre et d’aire de toutes les figures planes, la proportion qui permet de calculer la mesure d’un arc de cercle, celle qui permet de calculer l’aire d’un secteur de disque, la conversion d’unités de longueur et la conversion d’unités d’aire.
Lorsque tu fais face à un problème impliquant des figures planes, voici ce que tu devrais faire pour t’aider avant d’effectuer tes calculs :
-
Déterminer s’il s’agit d’un problème de périmètre ou d’un problème d’aire.
-
Uniformiser les unités de mesure.
-
Faire un schéma de la situation dans lequel tu inscris les données du problème.
-
Faire un plan des étapes de résolution.
Le tableau suivant peut t’aider à déterminer s’il s’agit d’un problème de périmètre ou d’un problème d’aire :
| Périmètre | Aire |
|---|---|
| Synonymes | |
|
|
| Exemples | |
|
|
| Unités | |
|
|
Pour calculer l’aire d’une figure décomposable, tu peux procéder de 2 façons :
-
Tu peux calculer l’aire de la figure au complet et soustraire l’aire des parties à enlever.
-
Tu peux commencer par découper ta figure décomposable en figures plus simples, comme des triangles, des rectangles, etc. Ensuite, tu calcules l’aire de chacune de ces parties, puis tu additionnes le tout.
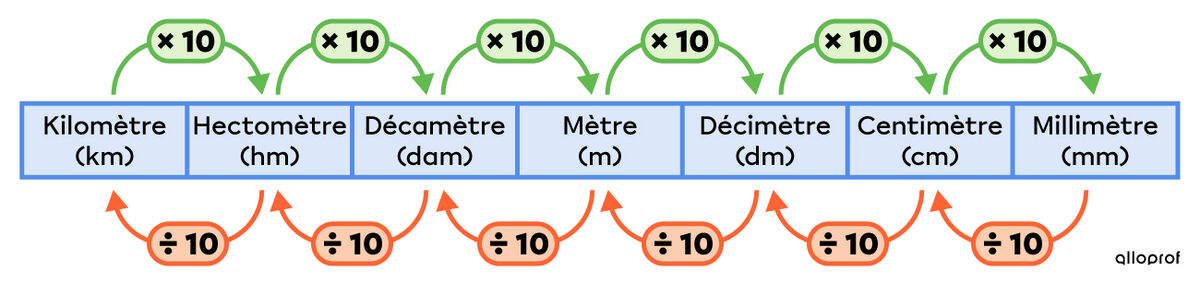
Voici le tableau de conversion des unités de longueur et celui de conversion des unités d’aire :
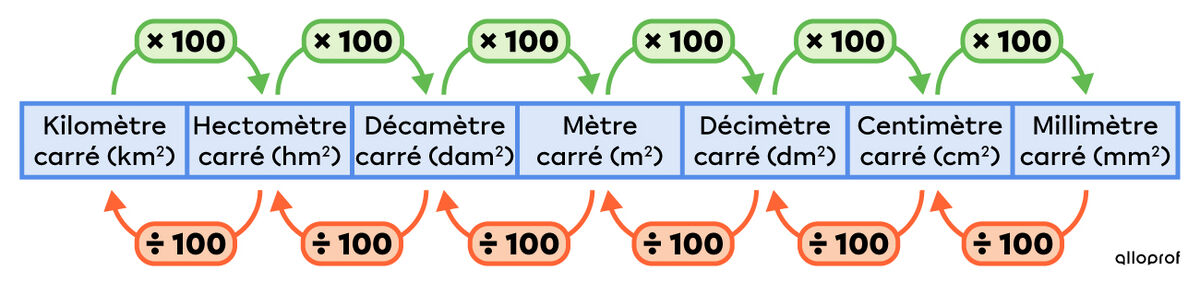
Voici les formules de périmètre et d’aire des figures planes :
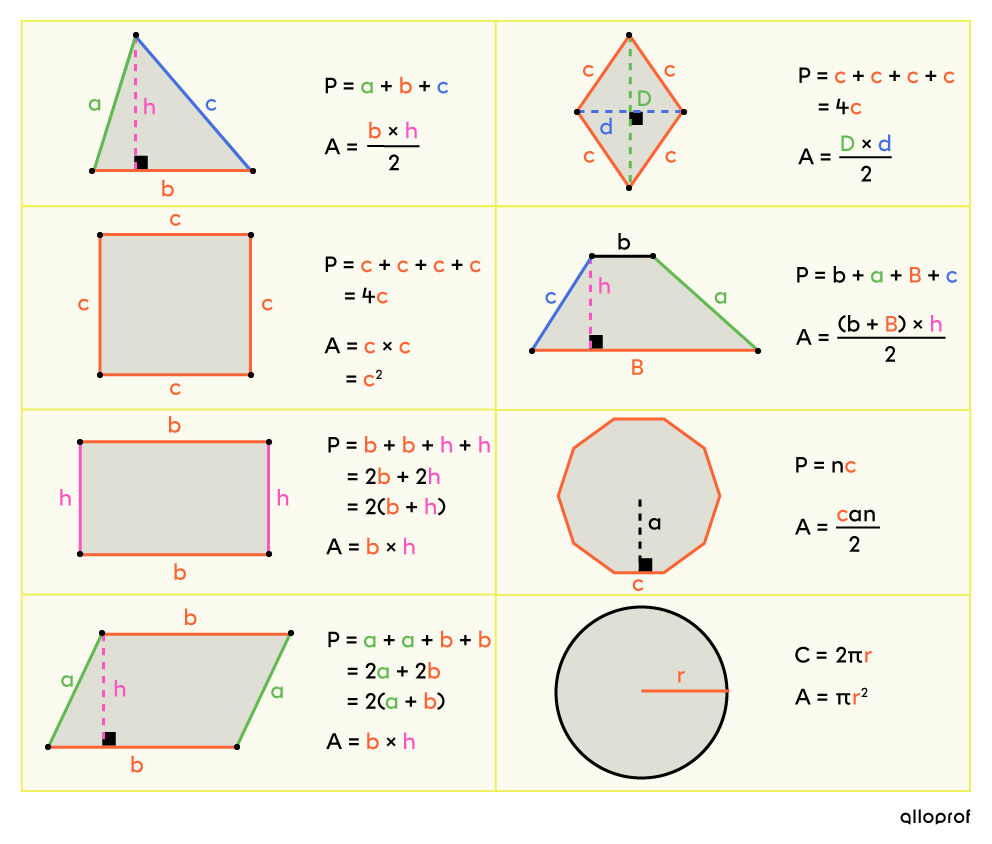
Pour calculer la mesure d’un arc de cercle ou l’aire d’un secteur de disque, tu dois utiliser l’une des 2 proportions suivantes : ||\dfrac{\text{Angle au centre}}{360^{\circ}}=\dfrac{\text{Arc de cercle}}{\text{Circonférence}}||ou||\dfrac{\text{Angle au centre}}{360^{\circ}}=\dfrac{\text{Aire du secteur}}{\text{Aire du disque}}||