A tangent equation or inequality contains a tangent ratio, where the unknown |(x)| is found in the argument.
Since the tangent function is periodic, this type of equation may have no solution, one solution, several solutions, or an infinite number of solutions.
Also, we need to use the angles in radians.
In the unit circle, the tangent of an angle corresponds to the ratio of the y-coordinate and the x-coordinate of the point on the circle. When solving a tangent equation, we can use the main points of the unit circle or the inverse function |\boldsymbol{\arctan}.|
When using the inverse function |\arctan,| the result obtained is always an angle in the 1st quadrant or the 4th quadrant of the unit circle. In other words, the angle is between |-\dfrac{\pi}{2}| and |\dfrac{\pi}{2}.|
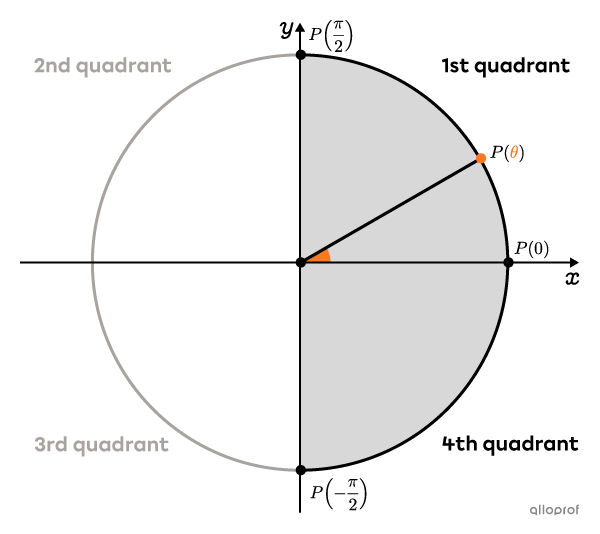
The inverse function |\arctan| is sometimes denoted |\tan^{-1},| especially on calculators.
There are some main values for the tangent ratio, which can be used when solving a tangent equation or inequality.
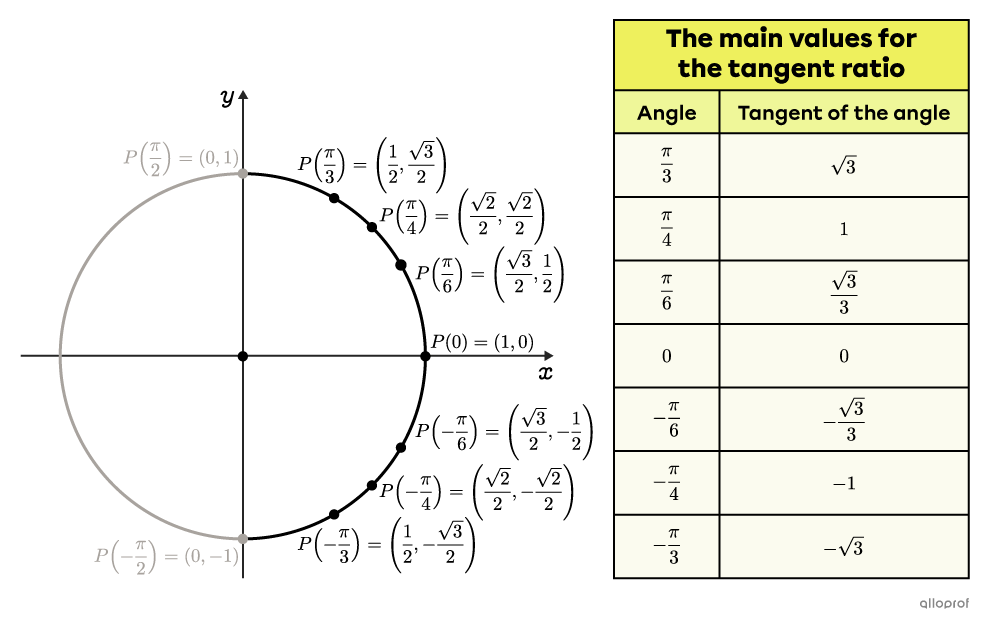
These values are obtained by dividing the |y| and |x| coordinates of the main points located in the 1st and 4th quadrants of the unit circle. Here's an example of the calculation using the angle |-\dfrac{\pi}{6}.| ||\begin{align}\tan\left(-\dfrac{\pi}{6}\right)&=\dfrac{\sin\left(-\dfrac{\pi}{6}\right)}{\cos\left(-\dfrac{\pi}{6}\right)}\\[3pt]&=\dfrac{-\dfrac{1}{2}}{\dfrac{\sqrt{3}}{2}}\\[3pt]&=-\dfrac{1}{\color{#ec0000}{\cancel{\color{black}{2}}}}\times\dfrac{\color{#ec0000}{\cancel{\color{black}{2}}}}{\sqrt{3}}\\[3pt]&=-\dfrac{1}{\sqrt{3}}\boldsymbol{\color{#ec0000}{\times\dfrac{\sqrt{3}}{\sqrt{3}}}}\\[3pt]&=-\dfrac{\sqrt{3}}{3}\end{align}||Note: There is no main value for the angles |\dfrac{\pi}{2}| and |-\dfrac{\pi}{2},| since we get a division by |0.| For this reason, the basic |\tan(x)| function has asymptotes at |x=\dfrac{\pi}{2}| and |x=-\dfrac{\pi}{2}.|
The procedure for solving a tangent equation is as follows:
-
Isolate the tangent ratio.
-
Determine the trigonometric angle using the table of main values or the inverse function |\boldsymbol{\arctan}.|
-
Solve the equation obtained with the trigonometric angle.
-
Calculate the period of the tangent function.
-
Give the solutions of the equation.
Here's an example using the table of main values of the tangent ratio to solve the equation.
Solve the following equation:||\tan(2x)-3=-2||
Solve the following equation:||\tan(2x)-3=-2||
-
Isolate the tangent ratio.
||\begin{align}\tan(2x)-3&=-2\\\tan(2x)&=1\end{align}|| -
Determine the trigonometric angle.
|
Angle |
Tangent of the angle |
|---|---|
|
||\dfrac{\pi}{3}|| |
||\sqrt{3}|| |
|
||\boldsymbol{\color{#fa7921}{\dfrac{\pi}{4}}}|| |
||\boldsymbol{\color{#c58ae1}{1}}|| |
|
||\dfrac{\pi}{6}|| |
||\dfrac{\sqrt{3}}{3}|| |
|
||0|| |
||0|| |
|
||-\dfrac{\pi}{6}|| |
||-\dfrac{\sqrt{3}}{3}|| |
|
||-\dfrac{\pi}{4}|| |
||-1|| |
|
||-\dfrac{\pi}{3}|| |
||-\sqrt{3}|| |
Since |\boldsymbol{\color{#c58ae1}{1}}| is a main value of the tangent ratio, we can determine the angles sought directly from the table of main values.
We find that the angle with a tangent ratio of |1| is |\boldsymbol{\color{#fa7921}{\dfrac{\pi}{4}}}.|
-
Solve the equation.
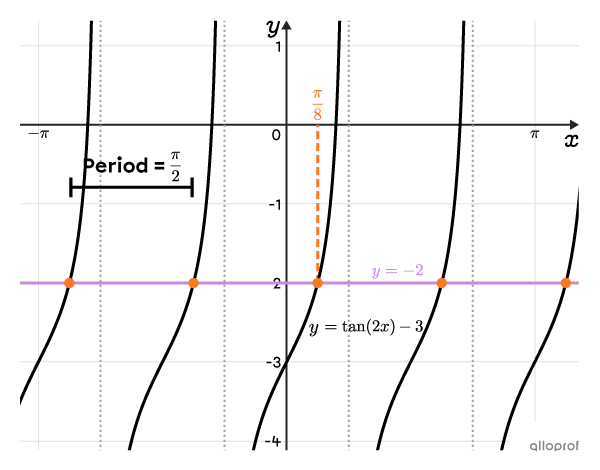
||\begin{align}\tan(2x)&=1\\ &\Downarrow\\2x&=\dfrac{\pi}{4}\\[3pt]\boldsymbol{\color{#fa7921}{x_1}}&=\boldsymbol{\color{#fa7921}{\dfrac{\pi}{8}}}\end{align}|| -
Calculate the period of the tangent function.
The tangent function is periodic, so we need to calculate the period in order to determine all the solutions.||\begin{align}p&=\dfrac{\pi}{\vert b\vert}\\[3pt]&=\dfrac{\pi}{\vert2\vert}\\[3pt]&=\dfrac{\pi}{2}\end{align}||
-
Give the solutions of the equation.
The solutions of the equation |\tan(2x)-3=-2| are as follows:
||x=\dfrac{\pi}{8}+\dfrac{\pi}{2}n||where||n\in\mathbb{Z}||
Here's an example using the inverse function arctangent to solve the equation.
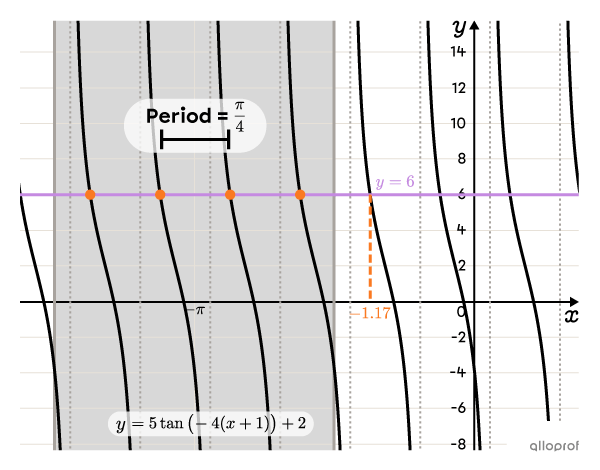
Solve the following equation for the interval |\left[-\dfrac{3\pi}{2},-\dfrac{\pi}{2}\right].|||5\tan\big(\!-4(x+1)\big)+2=6||
-
Isolate the tangent ratio.
||\begin{align}5\tan\big(\!-4(x+1)\big)+2&=6\\5\tan\big(\!-4(x+1)\big)&=4\\\tan\big(\!-4(x+1)\big)&=\dfrac{4}{5}\end{align}|| -
Determine the trigonometric angle.
We determine the angle sought using |\arctan.|||\begin{align}\tan\big(\!-4(x+1)\big)&=\dfrac{4}{5}\\&\Downarrow\\\boldsymbol{\color{#fa7921}{-4(x+1)}}&=\arctan\left(\dfrac{4}{5}\right)\\[3pt]&\approx\boldsymbol{\color{#fa7921}{0.67}}\end{align}||
-
Solve the equation.
We get the following equation that is formed from the angle found in the last step, and solve it.||\begin{align}-4(x+1)&\approx0.67\\x+1&\approx-0.17\\\boldsymbol{\color{#fa7921}{x_1}}&\approx\boldsymbol{\color{#fa7921}{-1.17}}\end{align}||
-
Calculate the period of the tangent function.
The tangent function is periodic, so we need to calculate the period in order to determine all the solutions.||\begin{align}p&=\dfrac{\pi}{\vert b\vert}\\[3pt]&=\dfrac{\pi}{\vert-4\vert}\\[3pt]&=\dfrac{\pi}{4}\end{align}||
-
Give the solutions of the equation.
Since we're looking for solutions within the interval |\left[-\dfrac{3\pi}{2},-\dfrac{\pi}{2}\right],| there are a finite number of solutions. The other solutions are calculated by adding or subtracting the period |\left(\dfrac{\pi}{4}\right)| to the value found in Step 3, without exceeding the interval.
We reject |-1.17,| since this value is larger than |-\dfrac{\pi}{2}.|||\begin{align}x&\approx-1.17-\dfrac{\pi}{4}\\[3pt]&\approx-1.95\end{align}||We keep |-1.95,| since this value is found inside the interval |\left[-\dfrac{3\pi}{2},-\dfrac{\pi}{2}\right].|||\begin{align}x&\approx-1.95-\dfrac{\pi}{4}\\[3pt]&\approx-2.74\end{align}||We keep |-2.74,| since this value is found inside the interval |\left[-\dfrac{3\pi}{2},-\dfrac{\pi}{2}\right].|||\begin{align}x&\approx-2.74-\dfrac{\pi}{4}\\[3pt]&\approx-3.52\end{align}||We keep |-3.52,| since this value is found inside the interval |\left[-\dfrac{3\pi}{2},-\dfrac{\pi}{2}\right].||\begin{align}x&\approx-3.52-\dfrac{\pi}{4}\\[3pt]&\approx-4.31\end{align}||We keep |-4.31,| since this value is found inside the interval |\left[-\dfrac{3\pi}{2},-\dfrac{\pi}{2}\right].|||\begin{align}x&\approx-4.31-\dfrac{\pi}{4}\\[3pt]&\approx-5.1\end{align}||We reject |-5.1,| since this value is less than |-\dfrac{3\pi}{2}.|
The solutions of the equation |5\tan\big(\!-4(x+1)\big)+2=6| for the interval |\left[-\dfrac{3\pi}{2},-\dfrac{\pi}{2}\right]| are the following:||x\in\{-4.31,\ -3.52,\ -2.74,\ -1.95\}||
Here's an example of solving a 2nd degree tangent equation.
Solve the following equation:||2\tan^2(x-2)-5\tan(x-2)+2=0||
A tangent equation of this type can be solved using the same strategies we use to solve a 2nd degree polynomial equation. In other words, you can use factoring or the quadratic formula.
To do so, we need to change the variable by replacing |\tan(x-2)| with |z.| This way, we can temporarily set aside the tangent ratios and concentrate on solving the 2nd degree polynomial.
The result is the following equation:||2\tan^2(x-2)-5\tan(x-2)+2=0\\\Updownarrow\\2z^2-5z+2=0||Using the quadratic formula, we obtain the following solutions for |z|:||\begin{align}z_{1,2}&=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}\\[3pt]&=\dfrac{-(-5)\pm\sqrt{(-5)^2-4(2)(2)}}{2(2)}\\[3pt]&=\dfrac{5\pm\sqrt{9}}{4}\\\\z_1&=\dfrac{1}{2}\quad\text{et}\quad z_2=2\end{align}||The solutions of the equation |2z^2-5z+2=0| are therefore |z_1=\dfrac{1}{2}| and |z_2=2.| Since we changed variables, we can substitute |z| with |\tan(x-2).| We get the following 2 equations:
||\tan(x-2)=\dfrac{1}{2}||
||\tan(x-2)=2||
We can now proceed as we would for a 1st degree tangent equation.
-
Isolate the tangent ratio.
The tangent ratio is already isolated in both equations.
-
Determine the trigonometric angles.
We determine the 2 angles sought using |\arctan| in both equations.
||\begin{align}\tan(x-2)&=\dfrac{1}{2}\\&\Downarrow\\\boldsymbol{\color{#fa7921}{x-2}}&=\arctan\left(\dfrac{1}{2}\right)\\[3pt]&\approx\boldsymbol{\color{#fa7921}{0.46}}\end{align}||
||\begin{align}\tan(x-2)&=2\\&\Downarrow\\\boldsymbol{\color{#51b6c2}{x-2}}&=\arctan(2)\\&\approx\boldsymbol{\color{#51b6c2}{1.11}}\end{align}||
-
Solve the equations.
We get the following 2 equations, which are formed using the angles found in the last step, and solve them.
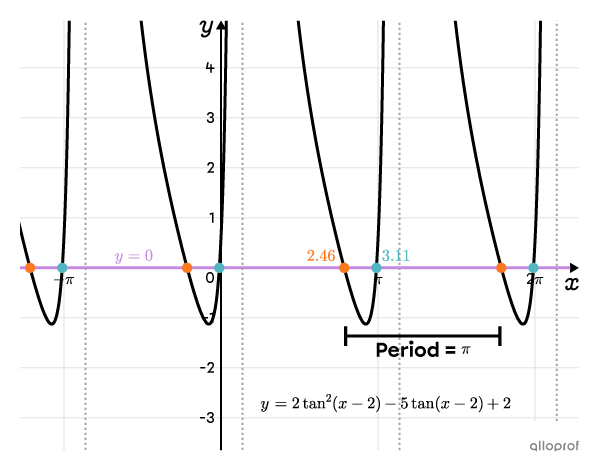
||\begin{align}x-2&\approx0.46\\\boldsymbol{\color{#fa7921}{x_1}}&\approx\boldsymbol{\color{#fa7921}{2.46}}\end{align}||
||\begin{align}x-2&\approx1.11\\\boldsymbol{\color{#51b6c2}{x_2}}&\approx\boldsymbol{\color{#51b6c2}{3.11}}\end{align}||
-
Calculate the period of the tangent function.
The tangent function is periodic, so we need to calculate the period in order to determine all the solutions.||\begin{align}p&=\dfrac{\pi}{\vert b\vert}\\[3pt]&=\dfrac{\pi}{\vert1\vert}\\[3pt]&=\pi\end{align}||
-
Give the solutions to the equation.
The solutions to the equation |2\tan^2(x-2)-5\tan(x-2)+2=0| are the following:
||x\in\left\{2.46+\pi n,\ 3.11+\pi n\right\}||where||n\in\mathbb{Z}||
We can use a technological tool to plot the solutions on the graph of the 2nd degree tangent function. Sketching this sort of graph is not part of the high school curriculum.
The procedure for solving a tangent inequality is as follows:
-
Change the inequality symbol to an equal symbol.
-
Isolate the tangent ratio.
-
Determine the trigonometric angle using the table of main values or the inverse function |\boldsymbol{\arctan}.|
-
Solve the equations obtained with the trigonometric angles.
-
Calculate the period of the tangent function.
-
Calculate the asymptotes of the tangent function.
-
Give the solution set of the inequality.
Here's an example using the table of main points tangent values to solve the inequality.
Solve the following inequality:||3\tan\left(\dfrac{x}{4}\right)>-\sqrt{3}||
-
Change the inequality symbol to an equal symbol.
||\begin{align}3\tan\left(\dfrac{x}{4}\right)&>-\sqrt{3}\\&\downarrow\\3\tan\left(\dfrac{x}{4}\right)&=-\sqrt{3}\end{align}|| -
Isolate the tangent ratio.
||\begin{align}3\tan\left(\dfrac{x}{4}\right)&=-\sqrt{3}\\[3pt]\tan\left(\dfrac{x}{4}\right)&=-\dfrac{\sqrt{3}}{3}\end{align}|| -
Determine the trigonometric angles.
|
Angle |
Tangent of the angle |
|---|---|
|
||\dfrac{\pi}{3}|| |
||\sqrt{3}|| |
|
||\dfrac{\pi}{4}|| |
||1|| |
|
||\dfrac{\pi}{6}|| |
||\dfrac{\sqrt{3}}{3}|| |
|
||0|| |
||0|| |
|
||\boldsymbol{\color{#fa7921}{-\dfrac{\pi}{6}}}|| |
||\boldsymbol{\color{#c58ae1}{-\dfrac{\sqrt{3}}{3}}}|| |
|
||-\dfrac{\pi}{4}|| |
||-1|| |
|
||-\dfrac{\pi}{3}|| |
||-\sqrt{3}|| |
Since |\boldsymbol{\color{#c58ae1}{-\dfrac{\sqrt{3}}{3}}}| is a main value of the tangent ratio, we can determine the angles sought directly from the table of main values.
We find that the angle with a tangent ratio of |-\dfrac{\sqrt{3}}{3}| is |\boldsymbol{\color{#fa7921}{-\dfrac{\pi}{6}}}.|
-
Solve the equations.
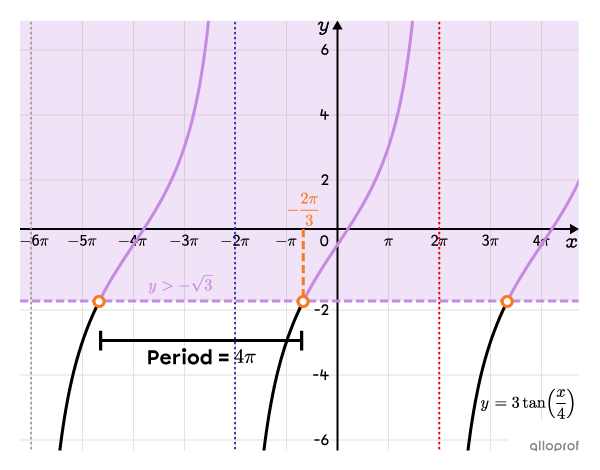
||\begin{align}\tan\left(\dfrac{x}{4}\right)&=-\dfrac{\sqrt{3}}{3}\\ &\Downarrow\\\dfrac{x}{4}&=-\dfrac{\pi}{6}\\[3pt]\boldsymbol{\color{#fa7921}{x_1}}&=\boldsymbol{\color{#fa7921}{-\dfrac{2\pi}{3}}}\end{align}|| -
Calculate the period of the tangent function.
The tangent function is periodic, so we need to calculate the period in order to determine all the solutions.||\begin{align}p&=\dfrac{\pi}{\vert b\vert}\\[3pt]&=\dfrac{\pi}{\vert\frac{1}{4}\vert}\\[3pt]&=4\pi\end{align}||
-
Calculate the asymptotes of the tangent function.
We calculate the asymptotes on either side of |\boldsymbol{\color{#fa7921}{x_1}}.|
Asymptote before |\boldsymbol{x_1}|
||\begin{align}\boldsymbol{\color{#333fb1}{x_0}}&=h-\dfrac{p}{2}\\[3pt]&=0-\dfrac{4\pi}{2}\\[3pt]&=\boldsymbol{\color{#333fb1}{-2\pi}}\end{align}||
Asymptote after |\boldsymbol{x_1}|
||\begin{align}\boldsymbol{\color{#ec0000}{x_2}}&=h+\dfrac{p}{2}\\[3pt]&=0+\dfrac{4\pi}{2}\\[3pt]&=\boldsymbol{\color{#ec0000}{2\pi}}\end{align}||
-
Give the solution set of the inequality.
There are 2 possible intervals: either between the lower asymptote |\boldsymbol{(\color{#333fb1}{x_0})}| and |\boldsymbol{\color{#fa7921}{x_1}},| or between |\boldsymbol{\color{#fa7921}{x_1}}| and the upper asymptote |\boldsymbol{(\color{#ec0000}{x_2})}.| To determine which interval is part of the solution set, we can use the graph or test an |x| value in each interval.
Note: Since the inequality symbol is |>,| the boundary associated with |\boldsymbol{\color{#fa7921}{x_1}}| is excluded from the solution set. Moreover, any boundary associated with an asymptote is always excluded.
||\left]\boldsymbol{\color{#333fb1}{-2\pi}},\boldsymbol{\color{#fa7921}{-\dfrac{2\pi}{3}}}\right[||Let’s test |x=-\pi.|||\begin{align}3\tan\left(\dfrac{x}{4}\right)&>-\sqrt{3}\\[3pt]3\tan\left(\dfrac{-\pi}{4}\right)&\overset{\text{?}}{>}-\sqrt{3}\\3\times-1&\overset{\text{?}}{>}-\sqrt{3}\\-3&\color{#ec0000}{\not>}-\sqrt{3}\end{align}||This inequality is false, which means that the interval |\left]\boldsymbol{\color{#333fb1}{-2\pi}},\boldsymbol{\color{#fa7921}{-\dfrac{2\pi}{3}}}\right[| is not part of the solution set.
||\left]\boldsymbol{\color{#fa7921}{-\dfrac{2\pi}{3}}},\boldsymbol{\color{#ec0000}{2\pi}}\right[||Let’s test |x=0.|||\begin{align}3\tan\left(\dfrac{x}{4}\right)&>-\sqrt{3}\\[3pt]3\tan\left(\dfrac{0}{4}\right)&\overset{\text{?}}{>}-\sqrt{3}\\3\times0&\overset{\text{?}}{>}-\sqrt{3}\\0&>-\sqrt{3}\end{align}||This inequality is true, which means that the interval |\left]\boldsymbol{\color{#fa7921}{-\dfrac{2\pi}{3}}},\boldsymbol{\color{#ec0000}{2\pi}}\right[| is part of the solution set.
Since the boundaries of the interval repeat themselves in every period, the solution set of the inequality |3\tan\left(\dfrac{x}{4}\right)>-\sqrt{3}| is as follows:
||x\in\left]-\dfrac{2\pi}{3}+4\pi n,\ 2\pi+4\pi n\right[||where||n\in\mathbb{Z}||
Here's an example using the inverse function arctangent to solve the inequality.
Solve the following inequality:||\dfrac{1}{4}\tan\big(2(x-\pi)\big)-6\le-5||
Solve the following inequality:||\dfrac{1}{4}\tan\big(2(x-\pi)\big)-6\le-5||
-
Change the inequality symbol to an equal symbol.
||\begin{align}\dfrac{1}{4}\tan\big(2(x-\pi)\big)-6&\le-5\\&\downarrow\\\dfrac{1}{4}\tan\big(2(x-\pi)\big)-6&=-5\end{align}|| -
Isolate the tangent ratio.
||\begin{align}\dfrac{1}{4}\tan\big(2(x-\pi)\big)-6&=-5\\[3pt]\dfrac{1}{4}\tan\big(2(x-\pi)\big)&=1\\[3pt]\tan\big(2(x-\pi)\big)&=4\end{align}|| -
Determine the trigonometric angles.
We determine the angle sought using |\arctan.|||\begin{align}\tan\big(2(x-\pi)\big)&=4\\&\Downarrow\\\boldsymbol{\color{#fa7921}{2(x-\pi)}}&=\arctan\left(4\right)\\&\approx\boldsymbol{\color{#fa7921}{1.33}}\end{align}||
-
Solve the equation.
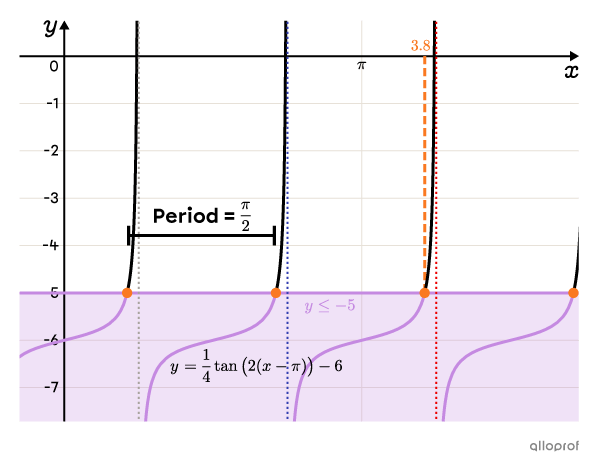
||\begin{align}2(x-\pi)&\approx1.33\\x-\pi&\approx0.66\\\boldsymbol{\color{#fa7921}{x_1}}&\approx\boldsymbol{\color{#fa7921}{3.8}}\end{align}|| -
Calculate the period of the tangent function.
The tangent function is periodic, so we need to calculate the period in order to determine all the solutions.||\begin{align}p&=\dfrac{\pi}{\vert b\vert}\\[3pt]&=\dfrac{\pi}{\vert2\vert}\\[3pt]&=\dfrac{\pi}{2}\end{align}||
-
Calculate the asymptotes of the tangent function.
We calculate the asymptotes on either side of |\boldsymbol{\color{#fa7921}{x_1}}.|
Asymptote before |\boldsymbol{x_1}|
||\begin{align}\boldsymbol{\color{#333fb1}{x_0}}&=h-\dfrac{p}{2}\\[3pt]&=\pi-\dfrac{\frac{\pi}{2}}{2}\\[3pt]&=\pi-\dfrac{\pi}{4}\\[3pt]&=\boldsymbol{\color{#333fb1}{\dfrac{3\pi}{4}}}\end{align}||
Asymptote after |\boldsymbol{x_1}|
||\begin{align}\boldsymbol{\color{#ec0000}{x_2}}&=h+\dfrac{p}{2}\\[3pt]&=\pi+\dfrac{\frac{\pi}{2}}{2}\\[3pt]&=\pi+\dfrac{\pi}{4}\\[3pt]&=\boldsymbol{\color{#ec0000}{\dfrac{5\pi}{4}}}\end{align}||
-
Give the solution set of the inequality.
There are 2 possible intervals: either between the lower asymptote |\boldsymbol{(\color{#333fb1}{x_0})}| and |\boldsymbol{\color{#fa7921}{x_1}},| or between |\boldsymbol{\color{#fa7921}{x_1}}| and the upper asymptote |\boldsymbol{(\color{#ec0000}{x_2})}.| To determine which interval is part of the solution set, we can use the graph or test an |x| value in each interval.
Note: Since the inequality symbol is |\le,| the boundary associated with |\boldsymbol{\color{#fa7921}{x_1}}| is included in the solution set. Moreover, any boundary associated with an asymptote is always excluded.
||\left]\boldsymbol{\color{#333fb1}{\dfrac{3\pi}{4}}},\boldsymbol{\color{#fa7921}{3.8}}\right]||Let’s test |x=\pi.|||\begin{align}\dfrac{1}{4}\tan\big(2(x-\pi)\big)-6&\le-5\\[3pt]\dfrac{1}{4}\tan\big(2(\pi-\pi)\big)-6&\overset{\text{?}}{\le}-5\\[3pt]\dfrac{1}{4}\tan(0)-6&\overset{\text{?}}{\le}-5\\[3pt]\dfrac{1}{4}\times0-6&\overset{\text{?}}{\le}-5\\[3pt]-6&\le-5\end{align}||This inequality is true, which means that the interval |\left]\boldsymbol{\color{#333fb1}{\dfrac{3\pi}{4}}},\boldsymbol{\color{#fa7921}{3.8}}\right]| is part of the solution set.
||\left[\boldsymbol{\color{#fa7921}{3.8}},\boldsymbol{\color{#ec0000}{\dfrac{5\pi}{4}}}\right[||Let’s test |x=3.85.|||\begin{align}\dfrac{1}{4}\tan\big(2(x-\pi)\big)-6&\le-5\\[3pt]\dfrac{1}{4}\tan\big(2(3{,}85-\pi)\big)-6&\overset{\text{?}}{\le}-5\\[3pt]\dfrac{1}{4}\times6.44-6&\overset{\text{?}}{\le}-5\\[3pt]-4.39&\color{#ec0000}{\not\le}-5\end{align}||This inequality is false, which means that the interval
|\left[\boldsymbol{\color{#fa7921}{3.8}},\boldsymbol{\color{#ec0000}{\dfrac{5\pi}{4}}}\right[| is not part of the solution set.
Since the boundaries of the interval repeat themselves in every period, the solution set of the inequality |\dfrac{1}{4}\tan\big(2(x-\pi)\big)-6\le-5| is as follows:
||x\in\left]\dfrac{3\pi}{4}+\dfrac{\pi}{2}n,\ 3.8+\dfrac{\pi}{2}n\right]||where||n\in\mathbb{Z}||
Here's an example of solving a 2nd degree tangent inequality.
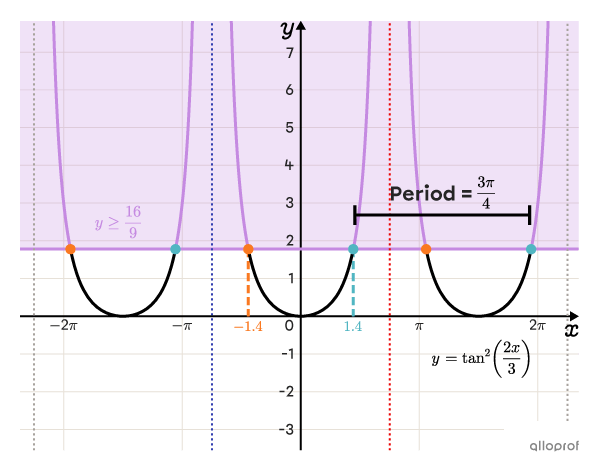
Solve the following inequality:||\tan^2\left(\dfrac{2x}{3}\right)\ge\dfrac{16}{9}||
-
Change the inequality symbol to an equal symbol.
||\begin{align}\tan^2\left(\dfrac{2x}{3}\right)&\ge\dfrac{16}{9}\\&\downarrow\\\tan^2\left(\dfrac{2x}{3}\right)&=\dfrac{16}{9}\end{align}|| -
Isolate the tangent ratio.
||\begin{align}\tan^2\left(\dfrac{2x}{3}\right)&=\dfrac{16}{9}\\[3pt]\tan\left(\dfrac{2x}{3}\right)&=\pm\sqrt{\dfrac{16}{9}}\\[3pt]\tan\left(\dfrac{2x}{3}\right)&=\pm\dfrac{4}{3}\end{align}|| -
Determine the trigonometric angles.
We determine the 2 angles sought by using |\arctan| in both equations.
||\begin{align}\tan\left(\dfrac{2x}{3}\right)&=-\dfrac{4}{3}\\&\Downarrow\\\boldsymbol{\color{#fa7921}{\dfrac{2x}{3}}}&=\arctan\left(-\dfrac{4}{3}\right)\\[3pt]&\approx\boldsymbol{\color{#fa7921}{-0.93}}\end{align}||
||\begin{align}\tan\left(\dfrac{2x}{3}\right)&=\dfrac{4}{3}\\&\Downarrow\\\boldsymbol{\color{#51b6c2}{\dfrac{2x}{3}}}&=\arctan\left(\dfrac{4}{3}\right)\\[3pt]&\approx\boldsymbol{\color{#51b6c2}{0.93}}\end{align}||
-
Solve the equations.
We get the following equations, formed using the angles found in the last step, and solve them.
||\begin{align}\dfrac{2x}{3}&\approx-0.93\\[3pt]\boldsymbol{\color{#fa7921}{x_1}}&\approx\boldsymbol{\color{#fa7921}{-1.39}}\end{align}||
||\begin{align}\dfrac{2x}{3}&\approx0.93\\[3pt]\boldsymbol{\color{#51b6c2}{x_2}}&\approx\boldsymbol{\color{#51b6c2}{1.39}}\end{align}||
-
Calculate the period of the tangent function.
The tangent function is periodic, so we need to calculate the period in order to determine all the solutions.||\begin{align}p&=\dfrac{\pi}{\vert b\vert}\\[3pt]&=\dfrac{\pi}{\left\vert\frac{2}{3}\right\vert}\\[3pt]&=\dfrac{3\pi}{2}\end{align}||
-
Calculate the asymptotes of the tangent function.
We calculate the asymptotes on either side of |\boldsymbol{\color{#fa7921}{x_1}}| and |\boldsymbol{\color{#51b6c2}{x_2}}.|
Asymptote before |\boldsymbol{x_1}|
||\begin{align}\boldsymbol{\color{#333fb1}{x_0}}&=h-\dfrac{p}{2}\\[3pt]&=0-\dfrac{\frac{3\pi}{2}}{2}\\[3pt]&=\boldsymbol{\color{#333fb1}{-\dfrac{3\pi}{4}}}\end{align}||
Asymptote after |\boldsymbol{x_2}|
||\begin{align}\boldsymbol{\color{#ec0000}{x_3}}&=h+\dfrac{p}{2}\\[3pt]&=0+\dfrac{\frac{3\pi}{2}}{2}\\[3pt]&=\boldsymbol{\color{#ec0000}{\dfrac{3\pi}{4}}}\end{align}||
-
Give the solution set of the inequality.
There are 3 possible intervals: between the lower asymptote |\boldsymbol{(\color{#333fb1}{x_0})}| and |\boldsymbol{\color{#fa7921}{x_1}};| between |\boldsymbol{\color{#fa7921}{x_1}}| and |\boldsymbol{\color{#51b6c2}{x_2}};| and between |\boldsymbol{\color{#51b6c2}{x_2}}| and the upper asymptote |\boldsymbol{(\color{#ec0000}{x_3})}.| To determine which interval is part of the solution set, we can use the graph or test an |x| value in each interval.
Note: Since the inequality symbol is |\ge,| the boundaries associated with |\boldsymbol{\color{#fa7921}{x_1}}| and |\boldsymbol{\color{#51b6c2}{x_2}}| are included in the solution set. Moreover, any boundary associated with an asymptote is always excluded.
||\left]\boldsymbol{\color{#333fb1}{-\dfrac{3\pi}{4}}},\boldsymbol{\color{#fa7921}{-1.39}}\right]||Let’s test |x=-\dfrac{\pi}{2}.|||\begin{align}\tan^2\left(\dfrac{2x}{3}\right)&\ge\dfrac{16}{9}\\[3pt]\tan^2\left(\dfrac{2\times-\frac{\pi}{2}}{3}\right)&\overset{\text{?}}{\ge}\dfrac{16}{9}\\[3pt]\tan^2\left(-\dfrac{\pi}{3}\right)&\overset{\text{?}}{\ge}\dfrac{16}{9}\\[3pt](-\sqrt{3})^2&\overset{\text{?}}{\ge}\dfrac{16}{9}\\[3pt]3&\ge\dfrac{16}{9}\end{align}||This inequality is true, which means that the interval |\left]\boldsymbol{\color{#333fb1}{-\dfrac{3\pi}{4}}},\boldsymbol{\color{#fa7921}{-1.39}}\right]| is part of the solution set.
||[\boldsymbol{\color{#fa7921}{-1.39}},\boldsymbol{\color{#51b6c2}{1.39}}]||Let’s test |x=0.|||\begin{align}\tan^2\left(\dfrac{2x}{3}\right)&\ge\dfrac{16}{9}\\[3pt]\tan^2\left(\dfrac{2\times0}{3}\right)&\overset{\text{?}}{\ge}\dfrac{16}{9}\\[3pt]\tan^2(0)&\overset{\text{?}}{\ge}\dfrac{16}{9}\\[3pt]0^2&\overset{\text{?}}{\ge}\dfrac{16}{9}\\[3pt]0&\color{#ec0000}{\not\ge}\dfrac{16}{9}\end{align}||This inequality is false, which means that the interval |[\boldsymbol{\color{#fa7921}{-1.39}},\boldsymbol{\color{#51b6c2}{1.39}}]| is not part of the solution set.
||\left[\boldsymbol{\color{#51b6c2}{1.39}},\boldsymbol{\color{#ec0000}{\dfrac{3\pi}{4}}}\right[||Let’s test |x=\dfrac{\pi}{2}.|||\begin{align}\tan^2\left(\dfrac{2x}{3}\right)&\ge\dfrac{16}{9}\\[3pt]\tan^2\left(\dfrac{2\times\frac{\pi}{2}}{3}\right)&\overset{\text{?}}{\ge}\dfrac{16}{9}\\[3pt]\tan^2\left(\dfrac{\pi}{3}\right)&\overset{\text{?}}{\ge}\dfrac{16}{9}\\[3pt]\sqrt{3}^2&\overset{\text{?}}{\ge}\dfrac{16}{9}\\[3pt]3&\ge\dfrac{16}{9}\end{align}||This inequality is true, which means that the interval |\left[\boldsymbol{\color{#51b6c2}{1.39}},\boldsymbol{\color{#ec0000}{\dfrac{3\pi}{4}}}\right[| is part of the solution set.
Since the boundaries of the interval repeat themselves in every period, the solution set of the inequality |\tan^2\left(\dfrac{2x}{3}\right)\ge\dfrac{16}{9}| is as follows:
||x\in\left]-\dfrac{3\pi}{4}+\dfrac{3\pi}{2}n,\,-1.39+\dfrac{3\pi}{2}n\right]\ \cup\ \left[1.39+\dfrac{3\pi}{2}n,\ \dfrac{3\pi}{4}+\dfrac{3\pi}{2}n\right[||where||n\in\mathbb{Z}||
We can use a technology tool to graph the 2nd degree tangent function. Drawing such a graph is not part of the high school curriculum.