La loi de Charles est une loi simple des gaz.
La loi de Charles est une relation mathématique qui décrit la relation entre le volume |(V)| et la température absolue |(T)| d’un gaz.
Pour modéliser la relation entre la température et le volume d’un gaz, on peut effectuer l’expérience suivante où la pression et la quantité de matière sont constantes.

On chauffe un gaz dans un cylindre creux fermé par un piston.
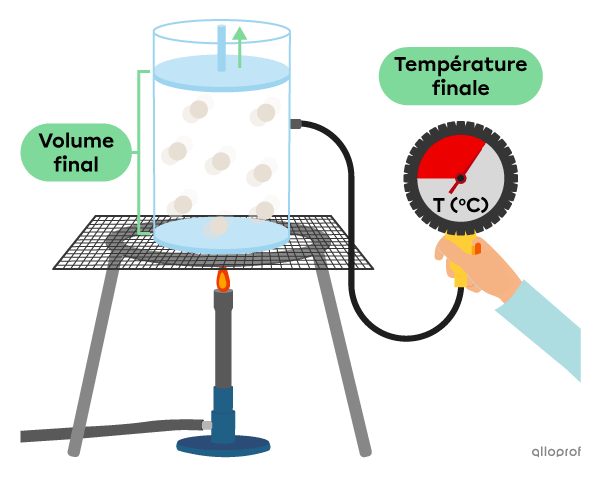
On chauffe le cylindre et on note l’augmentation de son volume en fonction de la température du gaz.

Les données obtenues décrivent une fonction de variation partielle.
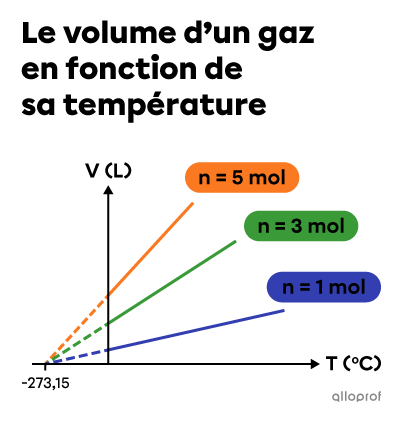
En réalisant la même expérience, mais avec des quantités de gaz différentes, on constate que les extrapolations des droites convergent toutes vers une même valeur d’abscisse à l’origine. En 1848, le physicien anglais Lord Kelvin établit cette valeur à |-273{,}15 ^\circ\text{C}.| Il s’agit du zéro absolu.

En utilisant l’échelle de température absolue, la relation entre le volume et la température d’un gaz lorsque la quantité (n) et la pression (P) sont constantes est décrite par une fonction de variation directe où le quotient |\dfrac{V}{T}| est constant.
L’échelle de température absolue est une échelle de mesure de la température où la température la plus basse admise correspond au zéro absolu |(-273{,}15 ^\circ\text{C}).| Il s’agit de la température théorique à laquelle l’énergie cinétique des particules serait nulle. Cette échelle ne présente aucune valeur négative et son unité de mesure est le kelvin |(\text{K}).|
||0\ \text{K}=-273{,}15\ ^\circ\text{C}||
Pour passer d’une température exprimée en degrés Celsius |(^\circ\text{C})| à une température exprimée en kelvins |(\text{K}),| on utilise la formule suivante.
||T_{\text{K}}=T_{^\circ\text{C}}+273{,}15||
La loi de Charles stipule que le volume |(V)| d’un gaz est directement proportionnel à sa température absolue |(T)| lorsque le nombre de moles |(n)| et la pression |(P)| sont constants. Elle s’exprime mathématiquement par l’expression suivante.
À |P| et |n| constants :
|V\propto\ T| où |\dfrac{V}{T}=\text{constante}|
où
|V : | Volume souvent en litres |(\text{L})|
|T : | Température absolue en kelvins |(\text{K})|
Puisque le quotient |\dfrac{V}{T}| est constant, on peut utiliser l’expression suivante pour comparer l’état initial et final d’un gaz.
||\dfrac{V_\text{1}}{T_\text{1}}=\dfrac{V_\text{2}}{T_\text{2}}||
où
|V_\text{1} : | Volume initial souvent en litres |(\text{L})|
|T_\text{1} : | Température initiale en kelvins |(\text{K})|
|V_\text{2} : | Volume final souvent en litres |(\text{L})|
|T_\text{2} : | Température finale en kelvins |(\text{K})|
La loi de Charles peut également s’expliquer grâce à la théorie cinétique des gaz.
Lorsqu’un gaz est chauffé, l’énergie cinétique de ses particules augmente. Puisque le mouvement des particules est amplifié, le gaz se dilate et occupe un plus grand volume. Ainsi, lorsque la température d’un gaz augmente, son volume augmente. À l’inverse, lorsque sa température diminue, son volume diminue.
Si un gaz est confiné dans un contenant, l’augmentation de sa température tend à faire augmenter le nombre et l’intensité des collisions entre ses particules et les parois du contenant dans lequel il se trouve. Dans un contenant de volume fixe, ceci ferait augmenter la pression du gaz. Dans un contenant de volume variable, le volume occupé par le gaz augmente au fur et à mesure que l’énergie cinétique des particules augmente, ce qui contribue à maintenir la pression constante.
Ainsi, si la température d’un gaz augmente, son volume tend à augmenter proportionnellement lorsque la quantité de matière et la pression sont constantes.
Les lois simples des gaz s’appliquent uniquement aux gaz parfaits.
Autrement dit, les valeurs calculées à l’aide des lois simples correspondent approximativement aux valeurs réelles, tant que la température du gaz n’est pas trop basse et que la pression n’est pas trop élevée.
On gonfle des ballons en préparation d’une fête d’anniversaire. Les ballons sont gonflés à l’intérieur de la maison, à une température de |20{,}00\ ^\circ\text{C}.| Chaque ballon contient un volume de |1{,}50\ \text{L}| d’air. Plus tard dans la journée, on installe les ballons à l’extérieur où la température est de |33{,}00\ ^\circ\text{C}.| Sachant que les ballons ont une capacité maximale de |1{,}80\ \text{L},| est-ce que les ballons sont à risque d’éclater?
-
On identifie les données et on convertit les degrés Celsius en kelvins.
|\begin{align}
V_1&=1{,}50\ \text{L}\\
T_1&=20{,}00\ ^\circ\text{C}+273{,}15=293{,}15\ \text{K}\\
V_2&=?\\
T_2&=33{,}00\ ^\circ\text{C}+273{,}15=306{,}15\ \text{K}\\
\end{align}|
On considère que la pression |(P)| et le nombre de moles de gaz |(n)| sont constants. -
On détermine la formule à utiliser
||\dfrac{V_\text{1}}{T_\text{1}}=\dfrac{V_\text{2}}{T_\text{2}}|| -
On isole |V_2| et on remplace les variables dans la formule.
|\begin{align}
V_2&=\dfrac{V_1\times T_2}{T_1}\\\\
V_2&=\dfrac{1{,}50\ \text{L}\times 306{,}15\ \text{K}}{293{,}15\ \text{K}}\\\\
V_2&\approx1{,}57\ \text{L}
\end{align}| -
On compare le volume final avec la capacité maximale des ballons.
|\begin{align}
V_{\text{max}}&=1{,}80\ \text{L}\\
V_2&=1{,}57\ \text{L}
\end{align}|
||1{,}57\ \text{L}\lt1{,}80\ \text{L}||
Le volume des ballons une fois à l’extérieur est d’environ |1{,}57\ \text{L}|, ce qui est inférieur à la capacité maximale des ballons |(1{,}80\ \text{L}).|
Les ballons ne sont pas à risque d’éclater une fois à l’extérieur.