La relation mathématique entre la pression et le nombre de moles est une loi simple des gaz.
La relation entre la pression |(P)| et le nombre de moles de gaz |(n)| est une loi qui décrit la relation mathématique entre ces deux variables lorsque le volume |(V)| et la température |(T)| sont constants.
On considère une certaine quantité de gaz dans un contenant incompressible à température constante.
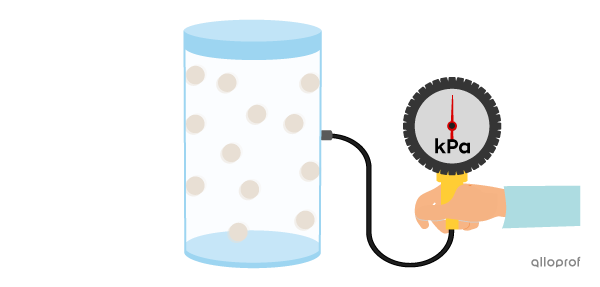
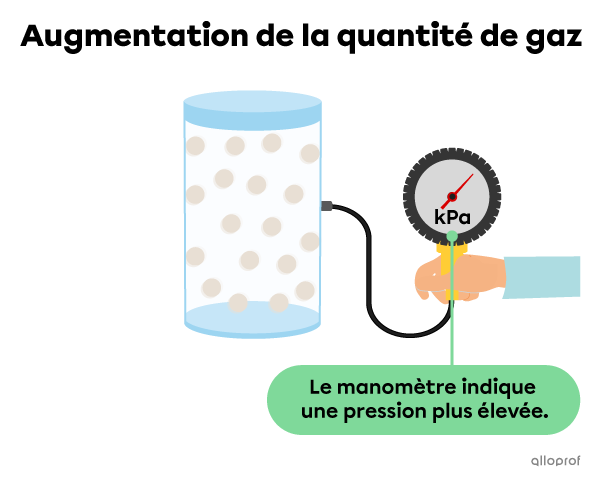
Si on augmente la quantité de gaz présente dans le contenant, les particules sont plus serrées, ce qui engendre davantage de collisions. Il y a alors une plus grande pression sur les parois du contenant.
Si on diminue la quantité de gaz présente dans le contenant, les particules sont moins serrées, alors le nombre de collisions diminue, ce qui diminue également la pression exercée par le gaz.
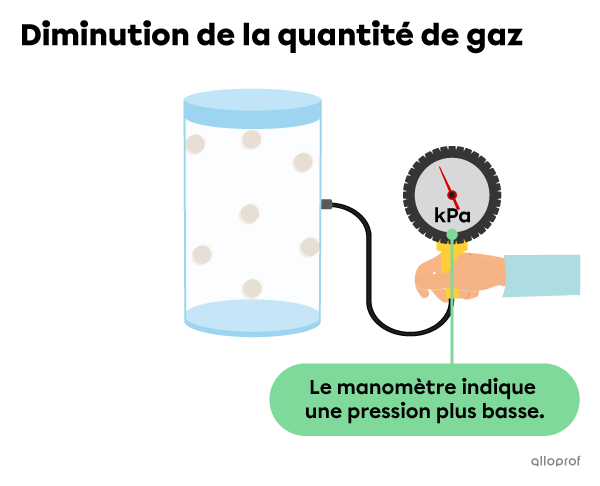
En somme, lorsque la température |(T)| et le volume |(V)| sont constants, plus la quantité de gaz augmente, plus la pression augmente. À l’inverse, plus la quantité de gaz diminue, plus la pression diminue.
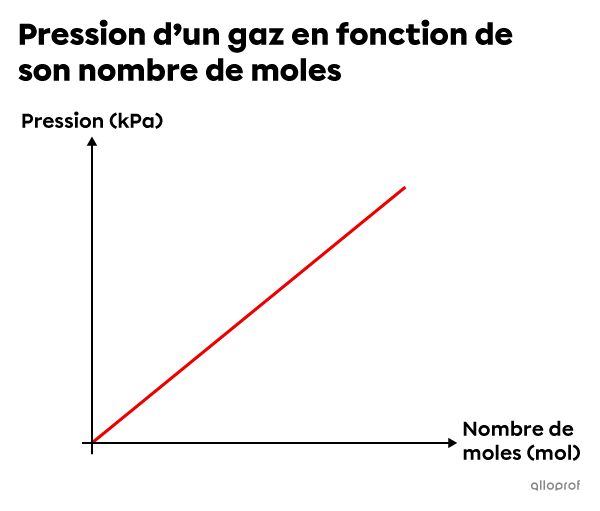
Ce graphique décrit la relation de variation directe qui unit la pression et le nombre de moles d’un gaz.
On dit que la pression d’un gaz est directement proportionnelle à son nombre de moles. Cette relation peut s’exprimer à l’aide de la formule suivante.
À |V| et |T| constants :
|P\propto n| ou |\dfrac{P}{n}=\text{constante}|
où
|P : | pression souvent en kilopascals |(\text{kPa})|
|n : | quantité de gaz en moles |(\text{mol})|
On peut aussi comparer une situation initiale et une situation finale dans laquelle la pression et le nombre de moles d’un gaz ont changé. La formule suivante peut alors être employée.
À |V| et |T| constants :
|\dfrac{P_1}{n_1} = \dfrac{P_2}{n_2}|
où
|P_1 : | pression initiale souvent en kilopascals |(\text{kPa})|
|n_1 : | quantité initiale de gaz en moles |(\text{mol})|
|P_2 : | pression finale souvent en kilopascals |(\text{kPa})|
|n_2 : | quantité finale de gaz en moles |(\text{mol})|
Les lois simples des gaz s’appliquent uniquement aux gaz parfaits.
Autrement dit, les valeurs calculées à l’aide des lois simples correspondent approximativement aux valeurs réelles, tant que la température du gaz n’est pas trop basse et que la pression n’est pas trop élevée.
Un pneu de voiture est crevé. Au départ, la pression d’air dans le pneu est de |220\ \text{kPa}| et la quantité de gaz est de |0{,}898\ \text{mol}.| Après un certain moment, |0{,}122\ \text{mol}| d’air se sont échappés du pneu.
Quelle est la pression d’air dans le pneu?
On considère que le volume du pneu et la température sont constants.
Un pneu de voiture est crevé. Au départ, la pression d’air dans le pneu est de |220\ \text{kPa}| et la quantité de gaz est de |0{,}898\ \text{mol}.| Après un certain moment, |0{,}122\ \text{mol}| d’air se sont échappés du pneu.
Quelle est la pression d’air dans le pneu?
On considère que le volume du pneu et la température sont constants.
-
On identifie les données.
|\begin{align}
P_1 &= 220\ \text{kPa}\\
n_1 &= 0{,}898\ \text{mol}\\
P_2 &=?\\
n_2 &= 0{,}898\ \text{mol} - 0{,}122\ \text{mol} = 0{,}776\ \text{mol}
\end{align}|
|V| et |T| sont constants.
-
On détermine la formule à utiliser. Puisque |V| et |T| sont constants, alors :
|\dfrac{P_1}{n_1} = \dfrac{P_2}{n_2}|
-
On isole la variable |P_2| et on remplace les données dans la formule.
|\begin{align}
P_2 &=\dfrac{P_1 \times n_2}{n_1}\\
P_2 &=\dfrac{220\ \text{kPa}\times 0{,}776\ \text{mol}}{0{,}898\ \text{mol}}\\
P_2 &\approx 190\ \text{kPa}
\end{align}|
La pression d’air dans le pneu est passée de |220\ \text{kPa}| à environ |190\ \text{kPa}.|
Vidéo à venir.
Exercices à venir.