To solve a problem involving a tangent function, it is often helpful to graph the situation. Generally, the rule of the tangent function must be found to answer the questions. Moreover, often a tangent equation must be solved.
The calculator must be set to radians (RAD) when working with trigonometric functions.
The main steps for solving a problem using the tangent function are as follows:
-
Identify the variables.
-
Place the information on the Cartesian plane and sketch the curve.
-
Find the rule of the function.
-
Answer the question(s).
Since tangent functions are periodic, there are many possible |x| values for any given |y| value.
Here is a video with an example of how to solve a problem involving a tangent function.
Enya is participating in a drone competition that requires her to perform a number of maneuvers. One of them follows a trajectory corresponding to a tangent function. The height of the drone is determined as a function of the horizontal distance between the drone and the competitor.
Here are the details of this trajectory:
-
At |11| metres high, the drone must be |9.38| metres away horizontally.
-
At a height of |15| metres, the drone must be approximately |10.65| metres away horizontally.
-
Enya must be situated at the origin of the Cartesian plane.
-
|11| metres from the competitor, there is a building along which the drone must fly.
a) What is the height of the drone when it is |2| metres away horizontally?
b) What horizontal distance did the drone travel when it is at a height of|12| metres?
c) If Enya’s drone is |1| metre away horizontally and |8| metres high, is she successfully following the trajectory?
-
Identify the variables.
|x:| horizontal distance (m)
|y:| height (m)
-
Place the information on the Cartesian plane and sketch the curve.
The first 2 details of the problem can be used to deduce two points: |(9.38,11)| and |(10.65,15).|
Since Enya is at the origin of the Cartesian plane, it is possible to deduce the first asymptote: |x=0.|
The building, located |11| metres away, represents the second asymptote: |x=11.|
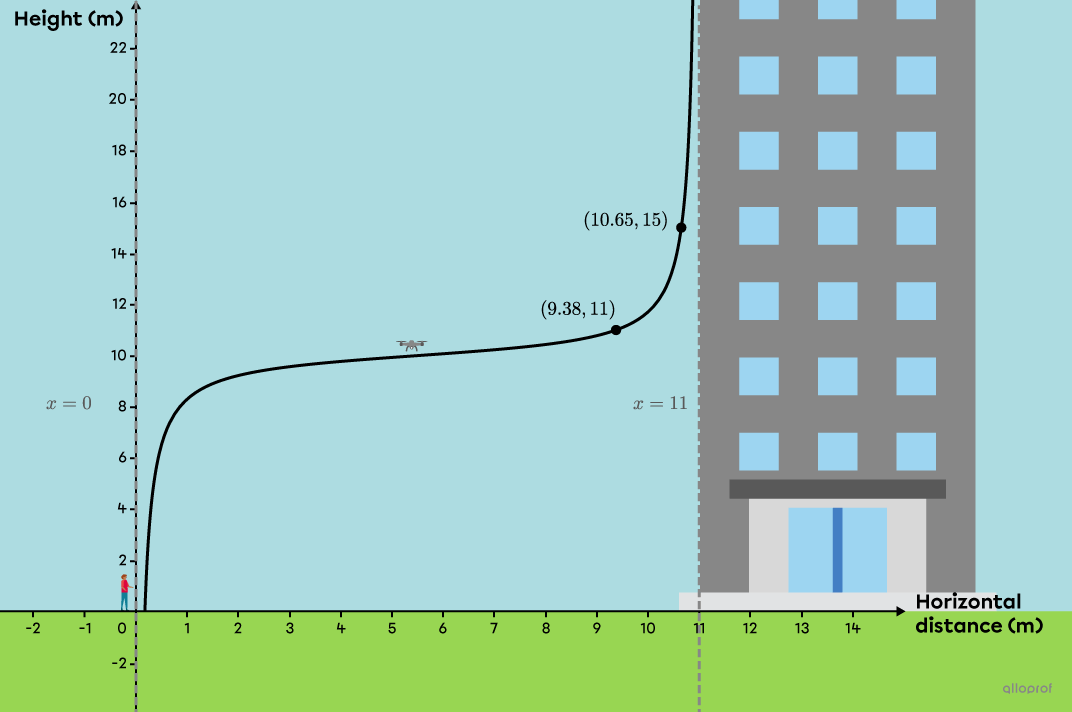
-
Find the rule of the function.
Finding the rule of the function allows questions to be answered with precision. The rule in standard form for a tangent function is |f(x)=a\tan\!\big(b(x-h)\big)+k.| With the information provided, we know 2 points and two consecutive asymptotes.
Determine the period from the 2 asymptotes
The value of the period is equal to the difference between the x-coordinates of the asymptotes.||p=11-0=11||
Determine the value of |b|
The |\vert b\vert| value is found from the period.||\begin{align}\vert b\vert&=\dfrac{\pi}{p}\\&=\dfrac{\pi}{11}\end{align}||To determine the sign of |b,| analyze the variation of the function. The graph indicates that the function is increasing. This means |a| and |b| have the same sign. A positive value can be used for both of these parameters.||b=\dfrac{\pi}{11}||
Determine the value of |h|
The |h| value is determined using the mean of the x-coordinates of the asymptotes.||h=\dfrac{11+0}{2}=5.5||
Create a system of equations and solve
Form 2 equations with 2 unknowns using the given points.
Point |(9.38,11)| gives the 1st equation.||11=\color{#3b87cd}a\tan\!\left(\dfrac{\pi}{11}(9.38-5.5)\right)+\color{#3A9A38}k||Isolate |k.|||\begin{align}11&=\color{#3b87cd}a\tan\!\left(\dfrac{\pi}{11}(3.88)\right)+\color{#3A9A38}k\\11&\approx\color{#3b87cd}a\tan(1.1081)+\color{#3A9A38}k\\11&\approx2\color{#3b87cd}a+\color{#3A9A38}k\\11-2\color{#3b87cd}a&\approx\color{#3A9A38}k\end{align}||
Point |(10.65,15)| gives the 2nd equation.||15=\color{#3b87cd}a\tan\!\left(\dfrac{\pi}{11}(10.65-5.5)\right)+\color{#3A9A38}k||Isolate |k.|||\begin{align}15&=\color{#3b87cd}a\tan\!\left(\dfrac{\pi}{11}(5.15)\right)+\color{#3A9A38}k\\15&\approx\color{#3b87cd}a\tan(1.4708)+\color{#3A9A38}k\\15&\approx9.97\color{#3b87cd}a+\color{#3A9A38}k\\15-9.97\color{#3b87cd}a&\approx\color{#3A9A38}k\end{align}||
Use the comparison method to find the value of |a.|||\begin{align}11-2\color{#3b87cd}a&=15-9.97\color{#3b87cd}a\\7.97\color{#3b87cd}a&=4\\\color{#3b87cd}{a}&\approx \color{#3b87cd}{0.5}\end{align}||The |k| value is determined using either of the 2 equations previously formed.||\begin{align}11-2\color{#3b87cd}a&=\color{#3A9A38}k\\11-2(\color{#3b87cd}{0.5})&=\color{#3A9A38}k\\10&=\color{#3A9A38}k\end{align}||The rule of the function is |f(x)=0.5\tan\left(\dfrac{\pi}{11}(x-5.5)\right)+10.|
-
Answer the question(s).
a) What is the height of the drone when it is |2| metres away horizontally?
Answering this question involves finding the value of |\color{#FA7921}{f(x)}| when |\color{#560FA5}{x=2}.|||\begin{align}\color{#FA7921}{f(x)}&=0.5\tan\left(\dfrac{\pi}{11}(\color{#560FA5}x-5.5)\right)+10\\\color{#FA7921}{f(x)}&=0.5\tan\left(\dfrac{\pi}{11}(\color{#560FA5}2-5.5)\right)+10\\\color{#FA7921}{f(x)}&=0.5\tan\left(\dfrac{\pi}{11}(-3.5)\right)+10\\\color{#FA7921}{f(x)}&\approx0.5(-1.556)+10\\\color{#FA7921}{f(x)}&\approx9.22\end{align}||Answer: When the drone is |2| metres away horizontally, it’s height is about |9.22| metres.
b) What horizontal distance did the drone travel when it is at a height of |12| metres?
This time, the value of |\color{#560FA5}x| when |\color{#FA7921}{f(x)=12}| is sought. A tangent equation must be solved.||\begin{align}\color{#FA7921}{f(x)}&=0.5\tan\left(\dfrac{\pi}{11}(\color{#560FA5}x-5{,}5)\right)+10\\\color{#FA7921}{12}&=0.5\tan\left(\dfrac{\pi}{11}(\color{#560FA5}x-5.5)\right)+10\\2&=0.5\tan\left(\dfrac{\pi}{11}(\color{#560FA5}x-5.5)\right)\\4&=\tan\left(\dfrac{\pi}{11}(\color{#560FA5}x-5.5)\right)\\\color{#EC0000}{\tan^{-1}(}4\color{#EC0000})&=\dfrac{\pi}{11}(\color{#560FA5}x-5.5)\\1.3258&\approx\dfrac{\pi}{11}(\color{#560FA5}x-5.5)\\4.6422&\approx\color{#560FA5}x-5.5\\10.14&\approx\color{#560FA5}x\end{align}||Answer: When the drone is |12| metres high, it will have travelled about |10.14| metres horizontally.
c) If Enya’s drone is |1| metre away horizontally and |8| metres high, is she successfully following the trajectory?
To answer this question, verify if the point |(1,8)| is part of the function. Replace |x| with |1| in the rule and verify if the answer is truly |8.|||\begin{align}\color{#FA7921}{f(x)}&=0.5\tan\left(\dfrac{\pi}{11}(\color{#560FA5}x-5.5)\right)+10\\\color{#FA7921}{f(1)}&=0.5\tan\left(\dfrac{\pi}{11}(\color{#560FA5}1-5.5)\right)+10\\\color{#FA7921}{f(1)}&\approx0.5\tan(-1.2852)+10\\\color{#FA7921}{f(1)}&\approx8.297\end{align}||Answer: Enya’s drone did not respect the trajectory, since it flew about |0.3| metres above the requested path.