The volume of a solid can be expressed using algebraic expressions. In this case, the measurements necessary for the calculations are expressed by monomials or polynomials. To solve this type of problem, a maximum of two variables are used to define the different measurements.
The volume of a solid relates to the space it occupies. It is possible to express the volume as an algebraic expression if the solid’s measurements are defined by variables or algebraic expressions. Thus, it is important to refer to the different formulas for calculating the volume of solids.
Sometimes a solid has missing measurements, in which case they are represented using variables or algebraic expressions. These algebraic expressions may be provided or it may be necessary to find them by mathematically translating the statement. A simplified algebraic expression can be obtained by applying the formulas for calculating volume.
The following example illustrates a problem where the algebraic expressions are given.
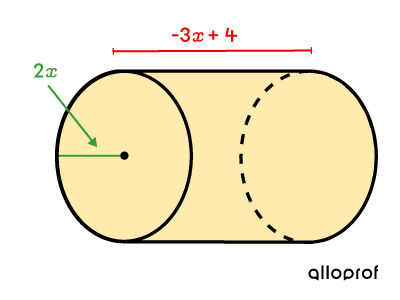
Determine the algebraic expression associated with the volume of the following cylinder.
-
Identify the algebraic expressions

-
Use the appropriate formula and substitute in the algebraic expressions||V=A_b\times \color{#EC0000}{h}\phantom{\times(-3x+4)}||
Since the base is a circle, use the formula for the area of a circle: ||\begin{align} V &= A_b \times \color{#EC0000}{h}\\&= \pi \color{#3A9A38}{r}^2\times \color{#EC0000}h\\&=\pi (\color{#3A9A38}{2x})^2\times (\color{#EC0000}{-3x+4}) \end{align}|| -
Simplify the algebraic expression||\begin{align} V&=\pi (\color{#3A9A38}{2x})^2\times (\color{#EC0000}{-3x+4})\\&=\pi(4x^2)\times (-3x+4)\\&=(4\pi x^2)\times (-3x+4)\\&=-12\pi x^3+16\pi x^2\\ &\approx -37{.}7x^3+50{.}27x^2\end{align}||
-
Interpret the answer
The algebraic expression for the volume of the cylinder is |-12\pi x^3+16\pi x^2|, or around |-37{.}7x^3+50{.}27x^2.|
The following example presents a problem where it is necessary to determine the algebraic expressions by mathematically translating the statement.
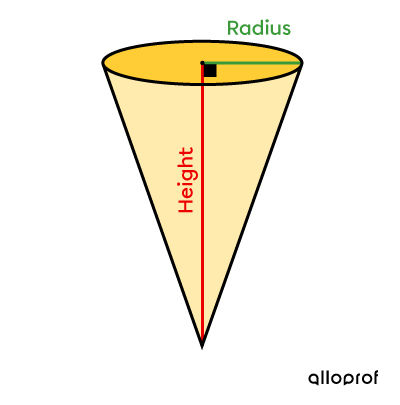
In an effort to keep the same proportions for cone-shaped candy containers, merchants insist that the height of the holders must be three units more than four times the measure of the radius.
With this information, determine the algebraic expression associated with the volume of the containers.
-
Represent the situation with a drawing, if necessary
-
Identify the algebraic expressions
In this scenario, the variable |x| can be assigned to one of the two dimensions. In this case, let |x| represent the radius. Therefore:
|\begin{align} \color{#3A9A38}{r} &= \color{#3A9A38}{x} \\ \color{#EC0000}{h} &= \color{#EC0000}{4x + 3}\end{align}|
The cone’s measurements can be represented as follows:

-
Use the appropriate formula and substitute in the algebraic expressions||\begin{align} V &= \dfrac{A_b \times \color{#EC0000}{h}}{3} \\\\ &=\dfrac{\pi \color{#3A9A38}{r}^2 \times \color{#EC0000}{h}}{3}\\\\ &= \frac{\pi \color{#3A9A38}{x}^2 \times (\color{#EC0000}{4x+3})}{3}\end{align}||
-
Simplify the algebraic expression||\begin{align} V &= \dfrac{\pi \color{#3A9A38}{x}^2 \times (\color{#EC0000}{4x+3})}{3} \\\\ &= \dfrac{4\pi x^3 +3\pi x^2}{3} \\\\ &= \dfrac{4}{3}\pi x^3 + \pi x^2 \\\\ &\approx 4{.}19x^3 + 3{.}14x^2\end{align}||
-
Interpret the answer
The exact algebraic expression for the volume of the holder is: |\dfrac{4}{3}\pi x^3+\pi x^2.|
The rounded algebraic expression associated with the volume is: |4{.}19x^3 + 3{.}14x^2.|
Note: The variable |r| could have been used for the radius. In this case, the height would be |4r +3.| The solution would be |\dfrac{4}{3}\pi r^3+\pi r^2.|
By associating algebraic expressions and variables with different measurements, it is possible to obtain the dimensions of all the solids that respect the constraints stated in the problem.
With a little more information, the numerical value associated with the variable used can be found.
Sometimes, none of the measurements are known, in which case algebraic expressions can be used to define the missing measurements. The advantage of using algebra is that it provides several possible answers.
What is the algebraic expression for the area of the base of a pyramid with a volume of |\dfrac{8}{3}x^2 - \dfrac{2}{3}x\ \text{cm}^3| and a height of |4x\ \text{cm?}|
-
Identify the formula
Use the formula for the volume of a pyramid. ||\phantom{\dfrac{8}{3}x^2 - \dfrac{2}{3}x}\color{#EC0000}{V} = \dfrac{A_b \times \color{#333FB1}{h}}{3}|| -
Replace variables with known values or algebraic expressions||\begin{align} \color{#EC0000}{V} &= \dfrac{A_b \times \color{#333FB1}{h}}{3} \\\\ \color{#EC0000}{\dfrac{8}{3}x^2 - \dfrac{2}{3}x } &= \dfrac{A_b\times \color{#333FB1}{4x}}{3} \end{align}||
-
Simplify and isolate the variable||\begin{align} \color{#EC0000}{\dfrac{8}{3}x^2 - \dfrac{2}{3}x } &= \dfrac{A_b\times \color{#333FB1}{4x}}{3} \\\\ 8x^2 - 2x &= A_b\times \color{#333FB1}{4x} \\ \\ \dfrac{8x^2-2x}{4x}&=A_b\\ 2x-0.5&=A_b \end{align}||
-
Interpret the answer
The algebraic expression associated with the area of the base is |2x -0.5.|
There are situations where factorization must be used to solve the problem. Here is an example.
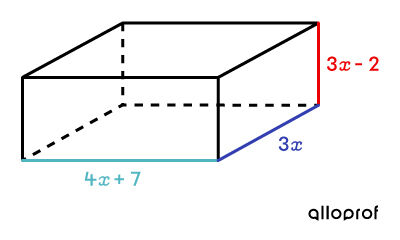
Find algebraic expressions for the all of the measurements of a rectangular prism that has a volume of |36 x^3 + 39x^2 - 42 x\ \text{cm}^3?|
-
Identify the formula
There is not enough information about the prism’s measurements to calculate its volume with the formula. Therefore, it is necessary to factor the polynomial. -
Factorization of the polynomial||\begin{align} &36x^3 + 39 x^2 - 42 x \\ =\ &3x (12x^2 + 13x - 14) && \text{Factoring out the greatest common factor} \\ =\ &3x (12x^2 +21x - 8x - 14) &&\text{Sum-product}\\ =\ &3x \big(3x (4x+7) - 2(4x+7)\big) &&\\ =\ &\color{#333FB1}{3x} \color{#51B6C2}{(4x+7)} \color{#EC0000}{(3x-2)}\end{align}||
-
Interpret the answer
Since calculating the prism’s volume consists of multiplying three factors, the algebraic expressions can be related with each of the prism’s dimensions as follows: