La réciproque de la fonction rationnelle

1. Interchanger |x| et |y.|

2. Isoler la variable dépendante |y| pour obtenir la fonction réciproque recherchée.

Quelle est la réciproque de la fonction rationnelle suivante? ||f(x)= \dfrac{-2}{5(x-1)}-2||

1. Interchanger |x| et |y| ||\begin{align}\color{#3b87cd}y&= \dfrac{-2}{5(\color{#ff55c3}x-1)}-2 \\ \color{#ff55c3}x &= \dfrac{-2}{5(\color{#3b87cd}y-1)}-2 \end{align}||

2. Isoler |y|
   On commence par isoler la fraction.||x+2= \dfrac{-2}{5(\color{#3B87CD}y-1)}||En utilisant les propriétés des proportions, on peut intervertir les extrêmes : |5(\color{#3B87CD}y-1)| et |x+2.| ||\color{#ec0000}{5(y-1)}= \dfrac{-2}{\color{#ec0000}{x+2}}||On finit d’isoler |\color{#3B87CD}y.| ||\begin{align} \color{#3B87CD}y-1 &= \dfrac{-2}{5(x+2)}\\ \color{#3B87CD}y &= \dfrac{-2}{5(x+2)}+1 \end{align}||

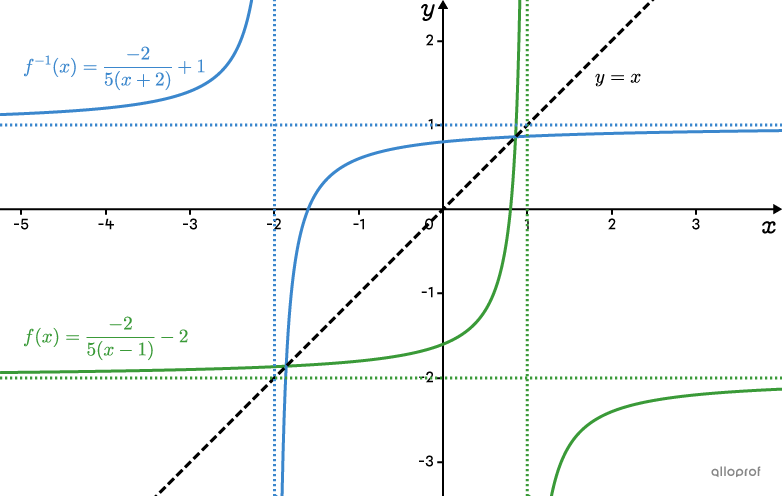
Réponse : La réciproque de |\color{#3a9a38}{f(x)= \dfrac{-2}{5(x-1)}-2}| est |\color{#3B87CD}{f^{-1}(x)=\dfrac{-2}{5(x+2)}+1}.|

Remarque : La règle de la réciproque est identique à la règle de la fonction de base à l’exception des paramètres |h| et |k| qui changent de place. 

Voici le graphique qui montre |\color{#3a9a38}{f(x)}| et |\color{#3B87CD}{f^{-1}(x)}.|

Quelle est la règle de la réciproque de la fonction rationnelle suivante? ||f(x)= \dfrac{5x+7}{3x+1}||

1. Interchanger |x| et |y| ||\begin{align} \color{#3B87CD}y &= \dfrac{5\color{#FF55C3}x+7}{3\color{#FF55C3}x+1} \\ \color{#FF55C3}x &= \dfrac{5\color{#3B87CD}y+7}{3\color{#3B87CD}y+1} \end{align}||

2. Isoler |y|
   On commence par faire un produit croisé.||\begin{align} \color{#FF55C3}x\times(3\color{#3B87CD}y+1) &= 5\color{#3B87CD}y+7 \\ 3\color{#FF55C3}x\color{#3B87CD}y+\color{#FF55C3}x &= 5\color{#3B87CD}y+7 \end{align}||On place les termes qui contiennent la variable |\color{#3B87CD}y| d’un côté et les autres termes de l’autre côté.||3\color{#FF55C3}x\color{#3B87CD}y-5\color{#3B87CD}y =-\color{#FF55C3}x + 7||On effectue une mise en évidence simple de |\color{#3B87CD}y| dans le membre de gauche de l'égalité.||\color{#3B87CD}y(3\color{#FF55C3}x-5) =-\color{#FF55C3}x + 7||On divise par |3\color{#FF55C3}x-5| pour isoler |\color{#3B87CD}y.| ||\color{#3B87CD}y=\dfrac{-\color{#FF55C3}x + 7}{3\color{#FF55C3}x-5}||

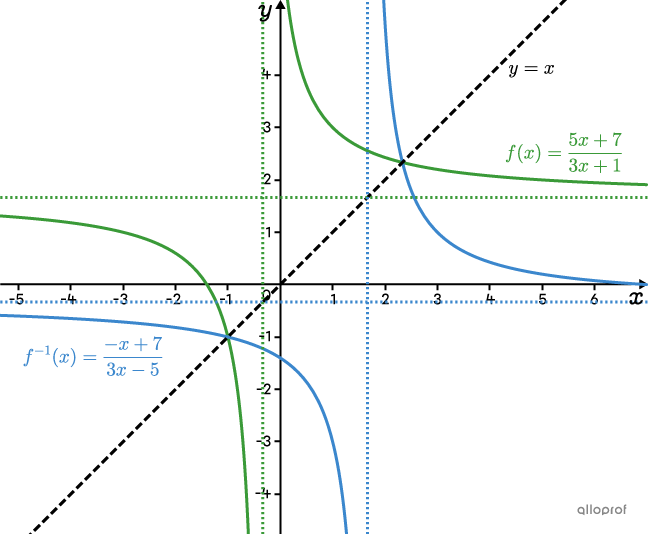
Réponse : La réciproque de |\color{#3a9a38}{f(x)= \dfrac{5x+7}{3x+1}}| est |\color{#3B87CD}{f^{-1}(x)=\dfrac{-x + 7}{3x-5}}.|

Voici le graphique qui montre |\color{#3a9a38}{f(x)}| et |\color{#3B87CD}{f^{-1}(x)}.|

Il est possible de tracer la réciproque d’une fonction en interchangeant les coordonnées |x| et |y| de certains points.

Par exemple, dans la figure ci-dessous, on peut observer la fonction |\color{#3a9a38}{f(x)=\dfrac{2}{5(x+1)}+2}| et sa réciproque : |\color{#3B87CD}{f^{-1}(x)=\dfrac{2}{5(x-2)}-1}.|

• L’ordonnée à l’origine de |\color{#3a9a38}{f(x)}| devient l’abscisse à l’origine de |\color{#3B87CD}{f^{-1}(x)}.| ||\color{#3a9a38}{(0;2{,}4)}\ \rightarrow\ \color{#3B87CD}{(2{,}4;0)}||

• L’abscisse à l’origine de |\color{#3a9a38}{f(x)}| devient l’ordonnée à l’origine de |\color{#3B87CD}{f^{-1}(x)}.| ||\color{#3a9a38}{(-1{,}2;0)}\ \rightarrow\ \color{#3B87CD}{(0;-1{,}2)}||

• Le point |\color{#3a9a38}{(1;2{,}2)}| devient le point |\color{#3B87CD}{(2{,}2;1)}| et ainsi de suite.

Il en est de même pour les asymptotes. L’asymptote verticale de |\color{#3a9a38}{f(x)}| devient l’asymptote horizontale de |\color{#3B87CD}{f^{-1}(x)}| et vice versa. ||\begin{align} &\color{#3a9a38}{x=-1}\ &&\rightarrow\ &&\color{#3B87CD}{y=-1}\\ &\color{#3a9a38}{y=2}\ &&\rightarrow\ &&\color{#3B87CD}{x=2} \end{align}||
 

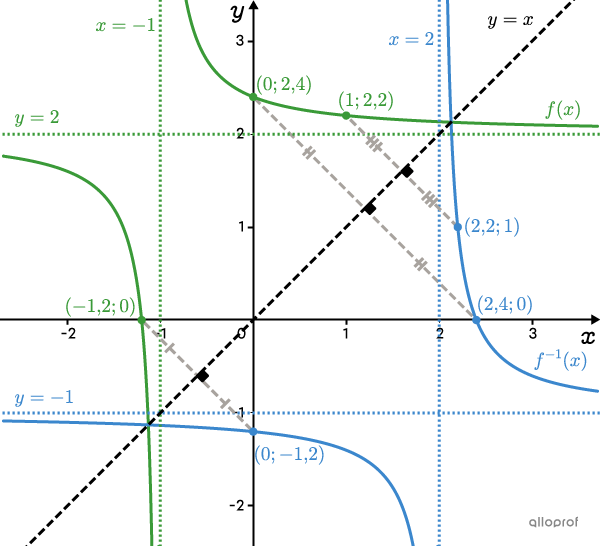
On peut aussi dire que |\color{#3B87CD}{f^{-1}(x)}| correspond à la réflexion de |\color{#3a9a38}{f(x)}| par rapport à l’axe d’équation |y=x.| Il est donc possible de tracer la réciproque par réflexion à condition que la graduation des axes |x| et |y| soit dans un rapport |1:1.|