La probabilité conditionnelle est la probabilité qu'un évènement |B| se produise sachant que l'évènement |A| s'est déjà produit. On la note |P(B \vert A).|
Il y a plusieurs façons de déterminer une telle probabilité selon le mode de représentation utilisé.
Il est possible de calculer une probabilité conditionnelle grâce à un diagramme en arbre. Pour y arriver, il suffit de trouver la bonne probabilité dans l’arbre.
On met |7| billes dans un récipient. Il y a |4| billes vertes |(V)| et |3| billes orange |(O).| On tire |2| billes sans remise. Quelle est la probabilité de piger une bille orange sachant qu'on a tiré une bille verte au 1er tirage?
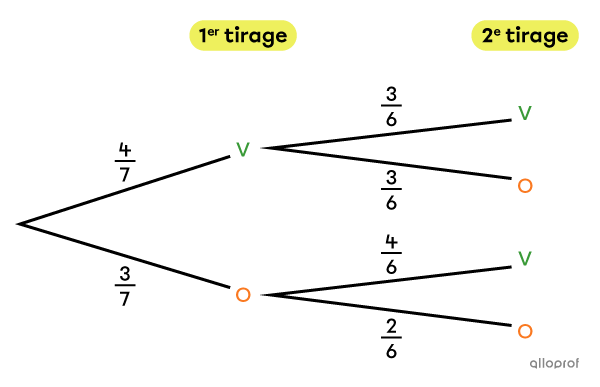
Puisqu’on sait que c’est une bille verte qui a été pigée au 1er tirage, on sait qu’on se trouve dans la partie supérieure du diagramme. On s’intéresse donc seulement aux 2 branches du 2e tirage pour répondre à la question. La probabilité d'obtenir une bille orange au 2e tirage est de |\dfrac{3}{6},| soit |\dfrac{1}{2}.|
Réponse : La probabilité de piger une bille orange sachant qu’on a pigé une bille verte au 1er tirage est |P(V\vert O)=\dfrac{1}{2}=50\ \%.|
Il est également possible de calculer une probabilité conditionnelle en utilisant une grille (tableau à double entrée).
Voici une étude réalisée dans un cinéma. Celle-ci s'intéresse aux types de films préférés des hommes et des femmes. Les choix sont divisés en 2 catégories : les films d'humour et les films d'horreur.
|
|
Humour |
Horreur |
Total |
|---|---|---|---|
|
Hommes |
23 |
67 |
90 |
|
Femmes |
75 |
24 |
99 |
|
Total |
98 |
91 |
189 |
On veut connaitre la probabilité que le type de film préféré d’une personne qui fréquente ce cinéma soit un film d'humour sachant que cette personne est un homme. Pour trouver la probabilité demandée, on doit seulement s’intéresser à la ligne Hommes du tableau, puisqu’on sait que c’est un homme qui est choisi. Il y a |23| hommes qui aiment les films d'humour sur un total de |90| hommes.
Réponse : La probabilité que le type de film préféré d’une personne soit un film d'humour sachant que cette personne est un homme est |P(\text{Humour}\vert \text{Homme})=\dfrac{23}{90}\approx 26\ \%.|
Lorsque les données sont présentées dans un diagramme de Venn ou sans mode de représentation, il est moins intuitif de déterminer des probabilités conditionnelles. Pour y arriver, on utilise plutôt une formule qui permet de calculer la probabilité d’un évènement |B| sachant que l’évènement |A| s’est déjà produit.
|P(B \vert A)=\dfrac{P(B \cap A)}{P(A)}|
où
|P(B \cap A) :| Intersection des évènements |B| et |A|
|P(A)>0|
On s'intéresse à la probabilité de piger une figure rouge dans un jeu de 52 cartes sachant que la carte pigée est une carte de carreau. Les évènements sont les suivants.
|A :| obtenir une carte de carreau
|B :| obtenir une figure rouge
Ainsi, on veut trouver |P(B \vert A).|
On représente la situation à l'aide d'un diagramme de Venn.
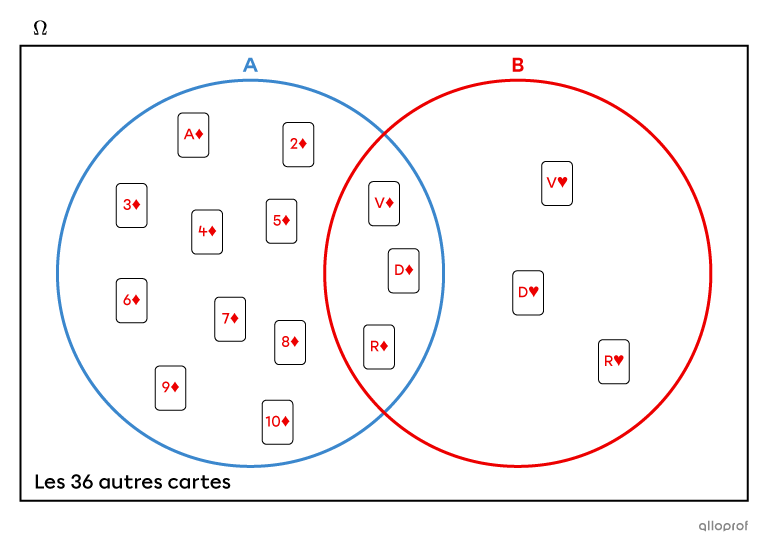
On utilise la formule |P(B \vert A) = \dfrac{P(B \cap A)}{P (A)}.|
La probabilité d’être dans l’intersection |(B \cap A)| est de |\dfrac{3}{52},| car il y a seulement |3| cartes sur les |52| qui sont en même temps dans les 2 ensembles : le roi, la dame et le valet de carreau.
La probabilité d’être dans l’ensemble |A| est de |\dfrac{13}{52}.| En effet, il y a |13| cartes de carreau dans le paquet.||\begin{align}P(B \vert A)&=\dfrac{P(B \cap A)}{P (A)}\\&=\dfrac{\ \ \dfrac{3}{52}\ \ }{\dfrac{13}{52}}\\&=\dfrac{3}{52} \times \dfrac{52}{13}\\&=\dfrac{3}{13}\end{align}||
Réponse : La probabilité de piger une figure rouge sachant qu'on a pigé une carte de carreau est de |\dfrac{3}{13},| soit environ |23\ \%.|
Voici un diagramme de Venn qui présente le nombre d'étudiants qui doivent reprendre un examen dans l’une ou l’autre des matières suivantes : mathématiques, français et/ou anglais.
Les évènements sont les suivants.
|M :| reprendre son examen de mathématiques
|F :| reprendre son examen de français
|A :| reprendre son examen d'anglais
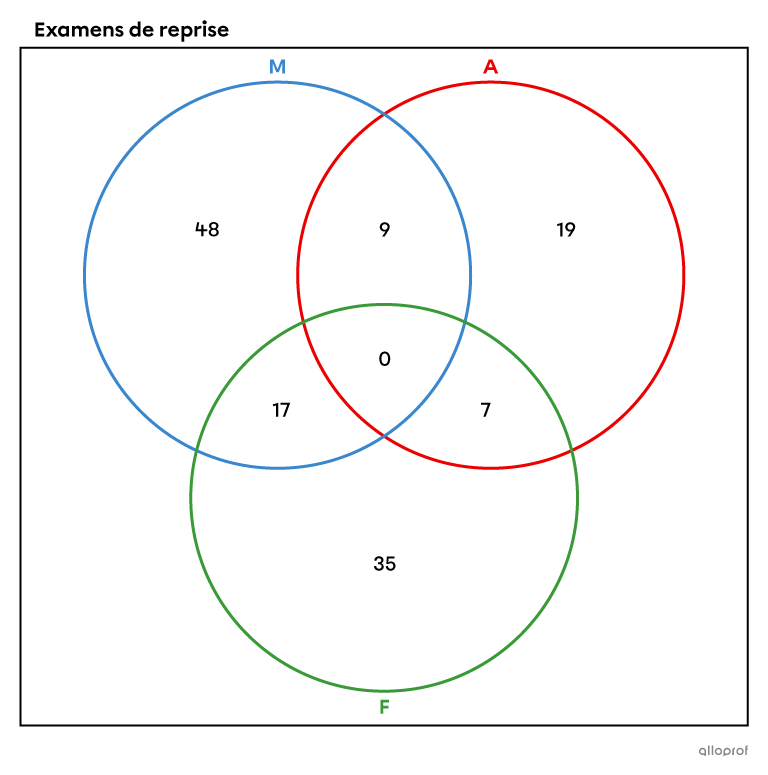
On veut savoir quelle est la probabilité qu'un élève reprenne son examen de mathématiques si on sait qu'il refait aussi son examen de français.
On cherche la probabilité de |M| sachant |F,| c’est-à-dire |P(M \vert F).|
On a besoin de |P(M \cap F)| et de |P(F).| On commence par déterminer le nombre d'élèves au total.||48+9+19+17+7+35=135|||P(M \cap F)| correspond à la probabilité qu'un élève reprenne son examen de mathématiques et celui de français. Cette probabilité est de |\dfrac{17}{135},| car il y a |17| élèves dans l’intersection sur un total de |135| élèves.
On doit aussi trouver |P(F).| Cette probabilité est de |\dfrac{59}{135},| car il y a |59| élèves au total dans l’ensemble |F| sur |135| élèves en tout. On peut maintenant calculer la probabilité conditionnelle.||\begin{align}P(M \vert F)&=\dfrac{P(M \cap F)}{P(F)}\\ &= \dfrac{\ \ \dfrac{17}{135}\ \ }{\ \ \dfrac{59}{135}\ \ }\\ &= \dfrac{17}{135} \times \dfrac{135}{59}\\ &=\dfrac{17}{59}\end{align}||
Réponse : La probabilité qu'un étudiant reprenne son examen de mathématiques sachant qu'il reprend déjà son examen de français est de |\dfrac{17}{59},| soit environ |29\ \%.|
Soit une expérience aléatoire comportant les évènements |A| et |B.| On sait que |P(A)=0{,}4,| |P(B)=0{,}7| et |P(A \cap B)=0{,}2.| Calcule |P(A \vert B)| et |P(B \vert A).|
Pour calculer la 1re probabilité conditionnelle, on utilise la formule.||\begin{align}P(A \vert B) &= \dfrac{P(A \cap B)}{P(B)}\\ &=\dfrac{0{,}2}{0{,}7}\\ &\approx 0{,}29\end{align}||Pour calculer la 2e probabilité conditionnelle, on utilise aussi la formule. Il est important de remarquer que l’intersection est commutative, donc |P(A \cap B) = P(B \cap A).|||\begin{align}P(B \vert A) &= \dfrac{P(B \cap A)}{P(A)}\\ &=\dfrac{0{,}2}{0{,}4}\\ &= 0{,}5\end{align}||
Réponses : ||\begin{align}P(A \vert B) &\approx 0{,}29 \\\\ P(B \vert A) &= 0{,}50\end{align}||
Il est également possible de répondre à d’autres questions en lien avec les informations de la question précédente.
Pour répondre à cette question, il faut se souvenir que 2 évènements sont indépendants si |P(A \cap B) = P(A) \times P(B).|
Il suffit de vérifier si cette condition est respectée.||\begin{align}P(A \cap B) &\overset{?}{=} P(A) \times P(B)\\0{,}2 &\overset{?}{=} 0{,}4 \times 0{,}7\\0{,}2 &\neq0{,}28 \end{align}||Comme la condition n’est pas respectée, on conclut que les évènements |A| et |B| sont dépendants.
Pour répondre à cette question, 2 évènements |(A| et |B)| sont mutuellement exclusifs si |P(A \cap B)=0.| Cela implique que |P(B \vert A)=0.| Or, ce n'est pas le cas. On conclut que les évènements |A| et |B| sont non mutuellement exclusifs.
Soit une expérience aléatoire comportant les évènements |A| et |B.| On sait que |P(B \vert A)=0{,}25| et |P(B \cap A)=0{,}2.| Calcule |P(A).|
On utilise la formule et on isole |P(A).|||\begin{align}P(B \vert A) &= \dfrac{P(B \cap A)}{P(A)}\\ 0{,}25&=\dfrac{0{,}2}{P(A)}\\ P(A)&= \dfrac{0{,}2}{0{,}25}\\P(A)&=0{,}8\end{align}||
Réponse : La probabilité de l’évènement |A| est de |0{,}8.|