The perimeter of any quadrilateral can always be determined by adding the measure of each side. The result is a length.
To determine the area of a quadrilateral, it is possible to use graph paper where each square has a specific area. By modifying the initial figure a little, the area of the quadrilateral can be determined.
By moving parts of the original quadrilateral, we can deduce the polygon has an area of |5\ \text{units}^2.|
It is possible to derive formulas for the perimeter and area specific to each quadrilateral based on their properties. The formulas are very useful for finding missing measurements.
Since the square is composed of 4 congruent sides and 4 right angles, we can derive formulas for the perimeter and area.
||\begin{align}P_\text{square}&=\color{#ec0000}a+\color{#3b87cd}b+\color{#3a9a38}c+\color{#fa7921}d\\
&=\color{#3a9a38}s+\color{#3a9a38}s+\color{#3a9a38}s+\color{#3a9a38}s\\
&=4\color{#3a9a38}s\end{align}||
Notice that the measure of one side of the square is the only information needed to calculate the perimeter.
To score a run in baseball, the player at bat must run to each base before finally returning to home plate. If a batter hits a homerun, the player can run the entire distance safely.
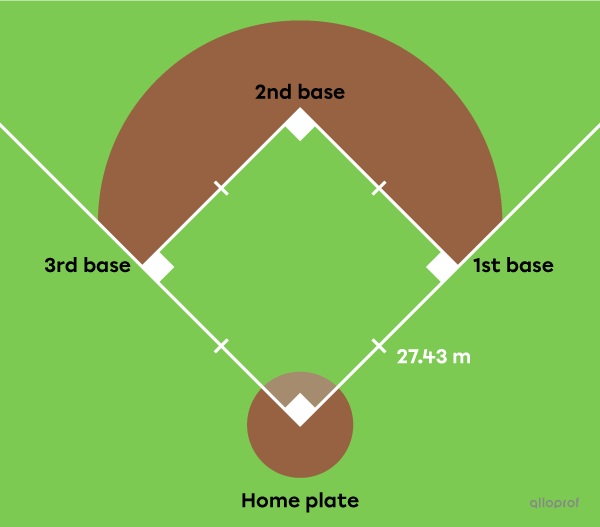
How far does a batter who hits a homerun have to travel before reaching home plate?
-
Identify the important measurements
||\color{#3a9a38}s=\color{#3a9a38}{27.43\ \text{m}}|| -
Find the perimeter
||\begin{align}P_\text{square}&=4\color{#3a9a38}s\\
&=4\times\color{#3a9a38}{27.43}\\
&=109.72\ \text{m}\end{align}|| -
Answer the question
The batter must travel a distance of |109.72\ \text{m}| before reaching home plate.
Just like calculating the perimeter, calculating the area of a square requires only the measure of one of its sides.
||\begin{align}A_\text{square}&=\color{#3a9a38}s\times \color{#3a9a38}s\\
&=\color{#3a9a38}s^2\end{align}||
where
|\color{#3a9a38}s:\text{side}|
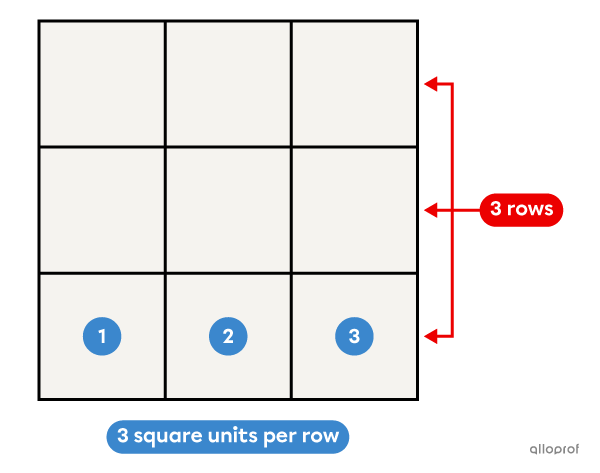
To calculate the area of a figure, we must determine the number of square units in the figure.
There are |\color{#ec0000}3| rows of |\color{#3b87cd}3| square units.
||\begin{align}A_\text{square}&=\text{Total number of square units}\\
&=\color{#ec0000}{3}\times\color{#3b87cd}{3}\\
&=\color{#ec0000}s\times\color{#3b87cd}s\\
&=s^2 \end{align}||
A homeowner wants to know the surface area of his house’s floor because he plans to install hardwood.
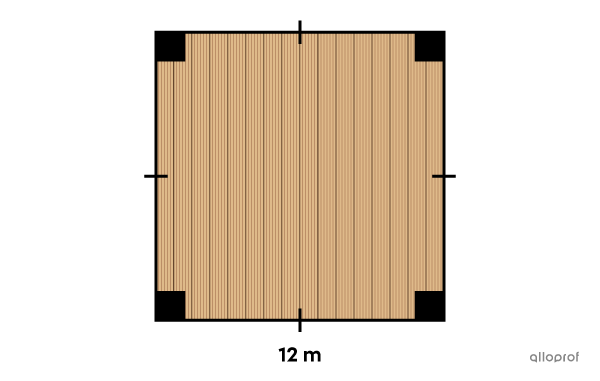
Does he have enough money with a budget of |\ $1\ 000| if the material desired costs
|\ $9.95/\text{m}^2?|
-
Identify the important measurements
||\color{#3a9a38}s=\color{#3a9a38}{12\ \text{m}}|| -
Find the area
||\begin{align}A_\text{square}&=\color{#3a9a38}s^2\\
&=\color{#3a9a38}{12}^2\\
&=144\ \text{m}^2\end{align}|| -
Answer the question
||\text{Cost} =144\times9.95=\$1\ 432.80\ ||
His |$1\ 000| budget will not be enough to install hardwood on his floor.
In a rectangle, the opposite sides are congruent and parallel. This property is useful when determining area and perimeter formulas.
||\begin{align}P_\text{rectangle}&=\color{#ec0000}a+\color{#3b87cd}b+\color{#3a9a38}c+\color{#fa7921}d\\
&= \color{#ec0000}h+\color{#ec0000}h+\color{#3b87cd}b+\color{#3b87cd}b\\
&=2\color{#ec0000}h+2\color{#3b87cd}b\\
&=2 (\color{#ec0000}h+\color{#3b87cd}b)\end{align}||
As shown in the previous box, the formula for the perimeter of a rectangle can be written several ways. Regardless of the formula chosen, the result is the same.
To install a border around his rectangular garden, Julian decides to install cement borders.
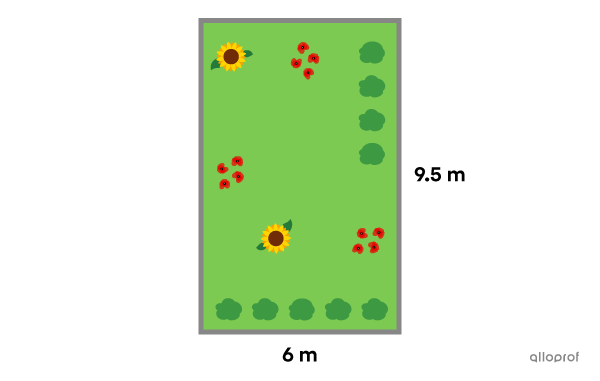
What is the cost of the installation if Julian knows a cement block of |90\ \text{cm}| in length costs |\$ 8.95?|
-
Identify the important measurements
||\begin{align}\color{#3b87cd}b&=\color{#3b87cd}{6\ \text{m}}\\
\color{#ec0000}h&=\color{#ec0000}{9.5\ \text{m}}\end{align}|| -
Find the perimeter
||\begin{align}P_\text{rectangle}&=2(\color{#3b87cd}b+\color{#ec0000}h)\\
&=2(\color{#3b87cd}6+\color{#ec0000}{9.5})\\
&=31\ \text{m}\\
&=3\ 100\ \text{cm}\end{align}|| -
Answer the question
||\text{Number of blocks}=3\ 100 \div 90 \approx 34.44||
Since we want to know how many blocks are needed, the answer must be a whole number. To install a border around the garden, |34| blocks are not enough. Julian must buy |35| blocks.
||\text{Cost}=35\times8.95=\$313.25\ ||
Julien must spend |\$ 313.25\ |on the border around his garden.
Note: The choices of the base and height were assigned randomly. In fact, the only connection between the base and the height is the fact they are perpendicular. We could have decided that |\color{#3b87cd}{b=9.5\ \text{m}}| and |\color{#ec0000}{h=6\ \text{m}}.| The result would have been the same.
||A_\text{rectangle}=\color{#3b87cd}b\times\color{#ec0000}h||
where
|\color{#3b87cd}b:\text{base}|
|\color{#ec0000}h:\text{height}|
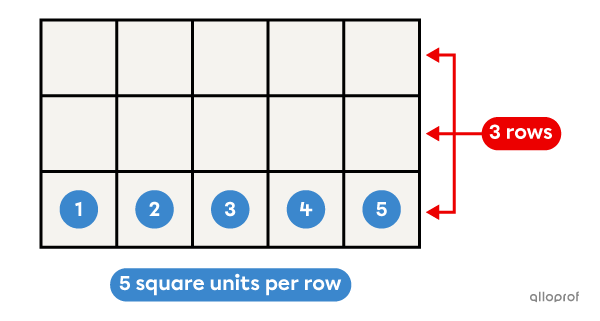
When we want to calculate the area of a figure, we have to determine the number of square units it is composed of. We simply perform a multiplication.
There are |\color{#ec0000}3| rows of |\color{#3b87cd}5| square units.
||\begin{align}A_\text{rectangle}&=\text{Total number of square units}\\
&=\color{#ec0000}3\times\color{#3b87cd}5\\
&=\color{#ec0000}h\times\color{#3b87cd}b\end{align}||
Since multiplication is commutative, we can say:
||A_\text{rectangle}=h\times b=b\times h||
Note: As in the application of the perimeter formula, the dimensions of the base and the height are randomly assigned, as long as the 2 segments are perpendicular.
To change the decor of a room, Suzy decides to paint one of the rectangular walls sky blue.

How much will the change cost her if a can of paint is sold for |\ $39.95,| and one can of paint covers an area of |20\ \text{m}^2?| She must also apply 3 coats of paint.
-
Identify the important measurements
||\begin{align}\color{#3b87cd}b&=\color{#3b87cd}{5.2\ \text{m}}\\
\color{#ec0000}h&=\color{#ec0000}{2.3\ \text{m}}\end{align}|| -
Find the area
||\begin{align}A_\text{rectangle}&= \color{#3b87cd}b\times \color{#ec0000}h\\
&=\color{#3b87cd}{5.2}\times\color{#ec0000}{2.3}\\
&=11.96\ \text{m}^2\end{align}|| -
Answer the question
Since we have to apply 3 coats, the area is tripled.
||\text{Area to paint}=11.96\times3=35.88\ \text{m}^2||
||\text{Number of cans needed}=35.88\ \text{m}^2\div 20\ \text{m}^2/\text{can} \approx 1.8\ \text{cans}||
Since we must buy full cans, Suzy needs 2 of them.
||\text{Cost}=2 \times39.95=\$79.90\ ||
The paint will cost |\ $79.90.|
Note: For problems related to the area of a figure, there is often more to do than just the calculation associated with the application of the formula. In such cases, it is important to understand the context of the problem.
The parallelogram's perimeter and area formulas are very similar to the rectangle’s.
||\begin{align}P_\text{parallelogram}&=\color{#3a9a38}a+\color{#3b87cd}b+\color{#ff55c3}c+\color{#fa7921}d\\
&=\color{#3a9a38}a+\color{#3b87cd}b+\color{#3a9a38}a+\color{#3b87cd}b\\
&=2\color{#3a9a38}a+2\color{#3b87cd}b\\
&=2(\color{#3a9a38}a+\color{#3b87cd}b)\end{align}||
As shown in the previous box, the formula for the perimeter of a parallelogram can be written in several ways. Regardless of the formula chosen, the result is the same.
Amélie runs in a park along a path that from a bird’s eye view forms a parallelogram. Her average running speed is |6\ \text{min/km}.| If she starts in front of the big tree and ends at the same spot, how long does her run last?

-
Identify the important measurements
||\begin{align}\color{#3b87cd}b&=\color{#3b87cd}{1.7\ \text{km}}\\
\color{#3a9a38}a&=\color{#3a9a38}{1.2\ \text{km}}\end{align}|| -
Find the perimeter
||\begin{align}P_\text{parallelogram}&=2(\color{#3a9a38}a+\color{#3b87cd}b)\\
&=2(\color{#3a9a38}{1.2}+\color{#3b87cd}{1.7})\\
&=5.8\ \text{km}\end{align}|| -
Answer the question
||\text{Run time: }5.8\ \text{km} \times 6\ \text{min/km} = 34.8\ \text{min}||
Amélie ran for almost |35| minutes.
||A_\text{parallelogram}=\color{#3b87cd}b\times \color{#ec0000}h||
where
|\color{#3b87cd}b:\text{base}|
|\color{#ec0000}h: \text{height}|
The area formula for a parallelogram is the same as a rectangle’s. To demonstrate it, simply grab a part of the parallelogram and move it to form a rectangle.
Note: The measure of the other pair of congruent sides |(\color{#3a9a38}a)| is not used in the area formula.
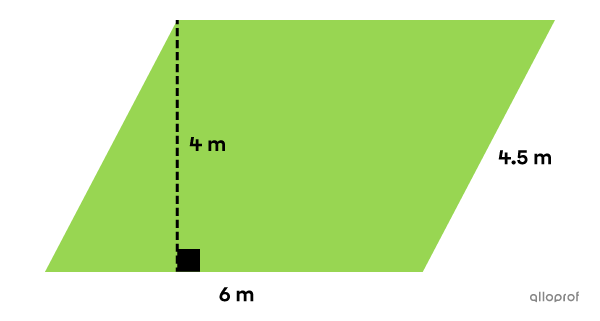
What is the area of the following parallelogram?
-
Identify the important measurements
||\begin{align}\color{#3b87cd}b&=\color{#3b87cd}{6\ \text{cm}}\\
\color{#ec0000}h&=\color{#ec0000}{4\ \text{cm}}\end{align}|| -
Find the area
||\begin{align}A_\text{parallelogram}&=\color{#3b87cd}b \times \color{#ec0000}h\\
&=\color{#3b87cd}6\times \color{#ec0000}4\\
&=24\ \text{cm}^2\end{align}|| -
Answer the question
The area of the parallelogram is |24\ \text{cm}^2.|
The area of a trapezoid, whether it is right-angled, isosceles, or otherwise, is always calculated with the same formula. However, the formula for the perimeter of a trapezoid can be tailored to the specific trapezoid.
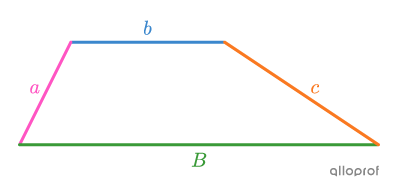
Trapezoid
||P_\text{trapezoid}= \color{#ff55c3}a+\color{#3b87cd}b+\color{#3a9a38}B+\color{#fa7921}c||
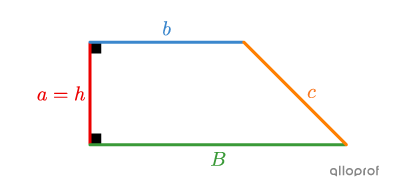
Right trapezoid
||\begin{align}P_\text{right trapezoid}&= \color{#ff55c3}a+\color{#3b87cd}b+\color{#3a9a38}B+\color{#fa7921}c\\&= \color{#ec0000}h+\color{#3b87cd}b+\color{#3a9a38}B+\color{#fa7921}c\end{align}||

Isosceles trapezoid
||\begin{align}P_\text{isosceles trapezoid}&= \color{#ff55c3}a+\color{#3b87cd}b+\color{#3a9a38}B+\color{#fa7921}c\\ &= \color{#ff55c3}a+\color{#3b87cd}b+\color{#3a9a38}B+\color{#ff55c3}a\\ &= 2\color{#ff55c3}a+\color{#3b87cd}b+\color{#3a9a38}B\end{align}||
Which one of the following trapezoids has the largest perimeter?
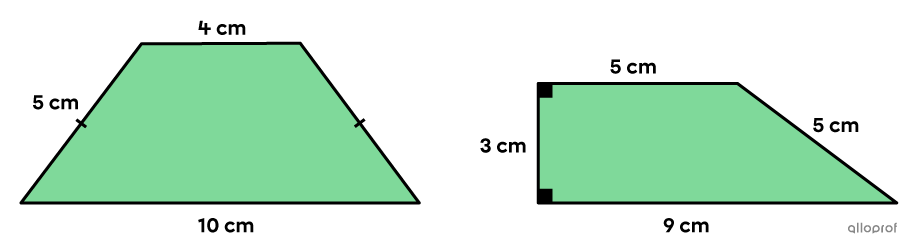
-
Identify the important measurements
Isosceles Trapezoid
||\begin{align}\color{#3b87cd}b&=\color{#3b87cd}{4\ \text{cm}}\\
\color{#3a9a38}B&=\color{#3a9a38}{10\ \text{cm}}\\
\color{#ff55c3}a&=\color{#ff55c3}{5\ \text{cm}}\end{align}||
Right Trapezoid
||\begin{align}\color{#3b87cd}b&=\color{#3b87cd}{5\ \text{cm}} \\
\color{#3a9a38}B&=\color{#3a9a38}{9\ \text{cm}}\\
\color{#ec0000}h&=\color{#ec0000}{3\ \text{cm}}\\
\color{#fa7921}c&=\color{#fa7921}{5\ \text{cm}}\end{align}||
-
Find the perimeters
||\begin{align}P_\text{isosceles trapezoid}&=2\color{#ff55c3}a+\color{#3b87cd}b+\color{#3a9a38}B\\
&=2\times\color{#ff55c3}5+\color{#3b87cd}4+\color{#3a9a38}{10}\\
&=24\ \text{cm}\end{align}||
||\begin{align}P_\text{right trapezoid}&=\color{#ec0000}h+ \color{#3b87cd}b+\color{#3a9a38}B+\color{#fa7921}c\\
&=\color{#ec0000}3+\color{#3b87cd}5+\color{#3a9a38}9+\color{#fa7921}5\\
&=22 \ \text{cm}\end{align}||
-
Answer the question
The perimeter of the isosceles trapezoid is the largest.
||A_\text{trapezoid}=\dfrac{(\color{#3a9a38}{B}+\color{#3b87cd}b)\times\color{#ec0000}h}{2}||
where
|\color{#3a9a38}B:\text{large base}|
|\color{#3b87cd}b:\text{small base}|
|\color{#ec0000}h:\text{height}|
To distinguish between each of the measurements used in the formula, refer to the properties of trapezoids. Note that the height always represents the distance measured perpendicular to the 2 bases.
To prove the formula, we use geometric transformations on some portions of a trapezoid to form a rectangle.
By doing so, we create a rectangle where the length is |\color{#3b87cd}b+\color{#3a9a38}B| and the height |\color{#ec0000}h| is the same as a trapezoid’s. Since the rectangle is composed of 2 trapezoids, we must divide by 2 to obtain the area of a trapezoid.
What is the area of the following trapezoid?
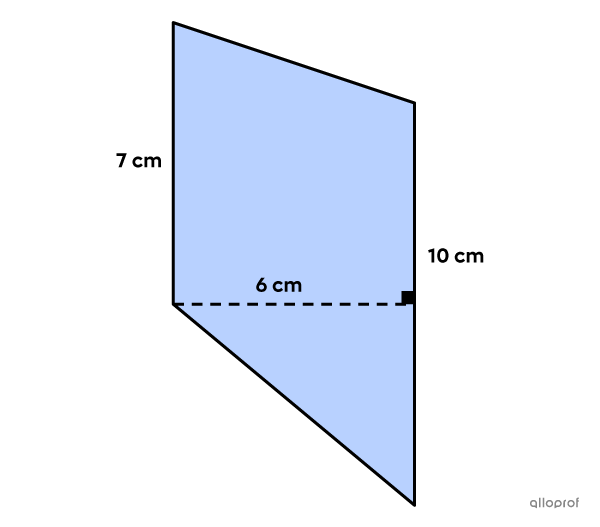
-
Identify the important measurements
||\begin{align}\color{#3a9a38}B&=\color{#3a9a38}{10\ \text{cm}}\\
\color{#3b87cd}b&=\color{#3b87cd}{7\ \text{cm}}\\
\color{#ec0000}h&=\color{#ec0000}{6 \ \text{cm}}\end{align}|| -
Find the area
||\begin{align}A_\text{trapezoid}&=\dfrac{(\color{#3a9a38}B+ \color{#3b87cd}b)\times\color{#ec0000}h}{2}\\
&=\dfrac{(\color{#3a9a38}{10}+\color{#3b87cd}7)\times \color{#ec0000}6}{2}\\
&=\dfrac{102}{2}\\
&=51\ \text{cm}^2\end{align}|| -
Answer the question
The area of the trapezoid is |51\ \text{cm}^2.|
||\begin{align}P_\text{rhombus}&=\color{#ff55c3}a+\color{#C58AE1}b+\color{#3a9a38}c+\color{#fa7921}d\\
&=\color{#3a9a38}s+\color{#3a9a38}s+\color{#3a9a38}s+\color{#3a9a38}s\\
&=4\color{#3a9a38}s\end{align}||
Only one measure is needed to calculate the perimeter of a rhombus.
What is the perimeter of the following rhombus?

-
Identify the important measurements
||\color{#3a9a38}s=\color{#3a9a38}{5.12\ \text{dm}}|| -
Find the perimeter
||\begin{align}P_\text{rhombus}&=4\color{#3a9a38}s\\
&=4\times\color{#3a9a38}{5.12}\\
&=20.48\ \text{dm}\end{align}|| -
Answer the question
The perimeter of the rhombus is |20.48\ \text{dm}.|
||A_\text{rhombus}=\dfrac{\color{#3b87cd}D\times\color{#ec0000}d}{2}||
where
|\color{#ec0000}d:\text{small diagonal}|
|\color{#3b87cd}D:\text{large diagonal}|
The formula for the area of a rhombus is related to the formula for the area of a rectangle. We can use a rotation to create a rectangle from a rhombus.
A rectangle is obtained with the area given by the following formula.
||\begin{align}A&=\color{#3b87cd}b\times\color{#ec0000}h\\
&=\color{#3b87cd}D\times\color{#ec0000}d\end{align}||
The rectangle is composed of 2 rhombuses. We must therefore divide the area of the rectangle by |2| to obtain the area of one rhombus.
||A_\text{rhombus}=\dfrac{\color{#3b87cd}D\times\color{#ec0000}d}{2}||
Theo has lost a card from his favorite deck of cards. It was the 7 of diamonds. Since he has a white card and some red paint, he decides to make a new card to replace it. The diamonds he paints are rhombi, all the same size. Given that one milliliter covers about |180\ \text{mm}^2,| how much paint will he need?

-
Identify the important measurements
||\begin{align}\color{#3b87cd}D&=\color{#3b87cd}{17\ \text{mm}}\\ \color{#ec0000}d&=\color{#ec0000}{13\ \text{mm}}\end{align}|| -
Find the area
||\begin{align}A_\text{rhombus}&=\dfrac{\color{#3b87cd}D\times \color{#ec0000}d}{2}\\
&=\dfrac{\color{#3b87cd}{17}\times\color{#ec0000}{13}}{2}\\
&=110.5\ \text{mm}^2\end{align}|| -
Answer the question
The area to determine is for one diamond. However, we must find the area of 7 diamonds.
||110.5 \times 7=773.5\ \text{mm}^2||
We can now find the amount of paint required.
||\begin{align}\dfrac{1\ \text{mL}}{180\ \text{mm}^2}&=\ \dfrac{?\ \text{mL}}{773.5\ \text{mm}^2}\\\\ ?&=\dfrac{1 \times 773.5}{180}\\?&\approx 4.3\ \text{mL}\end{align}||
About |4.3\ \text{mL}| of red paint is needed to duplicate the lost card.
||\begin{align}P_\text{kite}&=\color{#3a9a38}a+\color{#fa7921}b+\color{#ff55c3}c+\color{#C58AE1}d\\
&=\color{#3a9a38}a+\color{#3a9a38}a+\color{#fa7921}b+\color{#fa7921}b\\
&=2\color{#3a9a38}a+2\color{#fa7921}b\\
&=2(\color{#3a9a38}a+\color{#fa7921}b)\end{align}||
As illustrated in the previous box, the formula for the perimeter of the kite can be written in several ways. No matter which formula is chosen, the result is the same.
To protect the edges of a new kite, we want to buy plastic trim.

What is the total cost of the project if the material sells for |$1.95| per |10\ \text{cm?}|
-
Identify important measurements
||\begin{align}\color{#3a9a38}a&=\color{#3a9a38}{37\ \text{cm}}\\ \color{#fa7921}b&=\color{#fa7921}{52\ \text{cm}} \end{align}|| -
Find the perimeter
||\begin{align}P_\text{kite}&=2\color{#3a9a38}a+ 2\color{#fa7921}b\\
&=2\times\color{#3a9a38}{37}+2\times \color{#fa7921}{52}\\
&=178\ \text{cm}\end{align}|| -
Answer the question
Since it costs |$1.95| for |10\ \text{cm},| we conclude the following.
||\begin{align}\dfrac{$1.95}{10\ \text{cm}}&=\dfrac{\text{?}}{178\ \text{cm}}\\\\
\text{?}&=\dfrac{1.95 \times 178}{10}\\\\
\text{?}&=\ $34.71\end{align}||
It will cost |\ $34.71| to put protective trim on the kite’s edges.
||A_\text{kite}=\dfrac{\color{#ec0000}D\times \color{#3b87cd}d}{2}||
where
|\color{#ec0000}D:\text{large diagonal}|
|\color{#3b87cd}d:\text{small diagonal}|
The area formula of a kite is related to the rectangle's area formula. To understand where the formula comes from, refer to the proof of the formula for the area of a rhombus.
With changing weather conditions, a kite needs a new layer of water repellent for its surface so water won’t damage it.
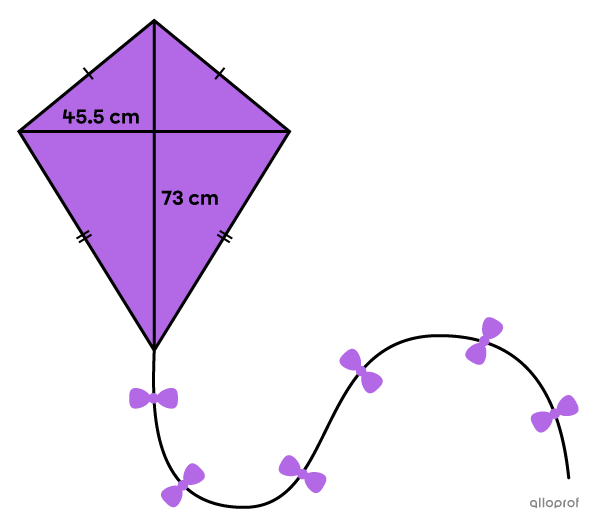
Assuming that both sides of the kite must be treated, how much product should be purchased if |10\ \text{mL}| can cover an area of |1\ \text{dm}^2?|
-
Identify the important measurements
||\begin{align}\color{#ec0000}D&=\color{#ec0000}{73\ \text{cm}}\\\color{#3b87cd}d&=\color{#3b87cd}{45.5\ \text{cm}}\end{align}|| -
Find the area
||\begin{align}A_\text{kite}&=\dfrac{\color{#ec0000}D \times \color{#3b87cd}d}{2}\\
&=\dfrac{\color{#ec0000}{73}\times \color{#3b87cd}{45.5}}{2}\\
&=1\ 660.75\ \text{cm}^2\\
&\approx 16.61\ \text{dm}^2\end{align}|| -
Answer the question
Since |10\ \text{mL}| is needed for |1\ \text{dm}^2,| we obtain the following for one side of the kite.
||\text{Total quantity}=16.61\ \text{dm}^2 \times 10\ \text{mL}/\text{dm}^2 = 166.1\ \text{mL}||
Since both sides of the kite must be painted, |166.1 \ \text{mL} \times 2 = 332.2\ \text{mL}| of paint is needed.