The inverse of a rational function is also a rational function.
Take the following steps to find the rule of the inverse of a rational function when the rule of the original function is known.
-
Interchange |x| and |y.|
-
Isolate the |y| variable to obtain the desired inverse function.
In the following example, the original function is in standard form.
What is the inverse of the following rational function?
||f(x)= \dfrac{-2}{5(x-1)}-2||
-
Interchange |x| and |y|
||\begin{align}\color{#3b87cd}y&= \dfrac{-2}{5(\color{#ff55c3}x-1)}-2 \\ \color{#ff55c3}x &= \dfrac{-2}{5(\color{#3b87cd}y-1)}-2 \end{align}|| -
Isolate |y|
Start by isolating the fraction.
||x+2= \dfrac{-2}{5(\color{#3B87CD}y-1)}||
Using the properties of proportions, invert the extremes: |5(\color{#3B87CD}y-1)| and |x+2.|
||\color{#ec0000}{5(y-1)}= \dfrac{-2}{\color{#ec0000}{x+2}}||
Finish by isolating |\color{#3B87CD}y.|
||\begin{align} \color{#3B87CD}y-1 &= \dfrac{-2}{5(x+2)}\\ \color{#3B87CD}y &= \dfrac{-2}{5(x+2)}+1 \end{align}||
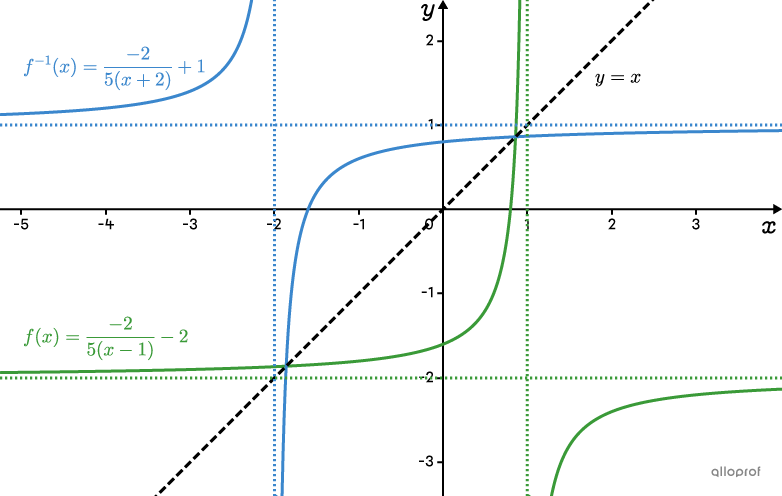
Answer: The inverse of |\color{#3a9a38}{f(x)= \dfrac{-2}{5(x-1)}-2}| is |\color{#3B87CD}{f^{-1}(x)=\dfrac{-2}{5(x+2)}+1}.|
Note: The inverse rule is identical to the original function rule, except parameters |h| and |k| have changed places.
The following graph indicates |\color{#3a9a38}{f(x)}| and |\color{#3B87CD}{f^{-1}(x)}.|
In the following example, the starting rule is given in general form.
What is the rule for the inverse of this rational function?
||f(x)= \dfrac{5x+7}{3x+1}||
-
Interchange |x| and |y|
||\begin{align} \color{#3B87CD}y &= \dfrac{5\color{#FF55C3}x+7}{3\color{#FF55C3}x+1} \\ \color{#FF55C3}x &= \dfrac{5\color{#3B87CD}y+7}{3\color{#3B87CD}y+1} \end{align}|| -
Isolate |y|
Start with cross-multiplication.
||\begin{align} \color{#FF55C3}x\times(3\color{#3B87CD}y+1) &= 5\color{#3B87CD}y+7 \\ 3\color{#FF55C3}x\color{#3B87CD}y+\color{#FF55C3}x &= 5\color{#3B87CD}y+7 \end{align}||
Place the terms with variable |\color{#3B87CD}y| on one side and the other terms on the opposite side.
||3\color{#FF55C3}x\color{#3B87CD}y-5\color{#3B87CD}y =-\color{#FF55C3}x + 7||
Factor out |\color{#3B87CD}y| on the left side of the equality.
||\color{#3B87CD}y(3\color{#FF55C3}x-5) =-\color{#FF55C3}x + 7||
Divide by |3\color{#FF55C3}x-5| to isolate |\color{#3B87CD}y.|
||\color{#3B87CD}y=\dfrac{-\color{#FF55C3}x + 7}{3\color{#FF55C3}x-5}||
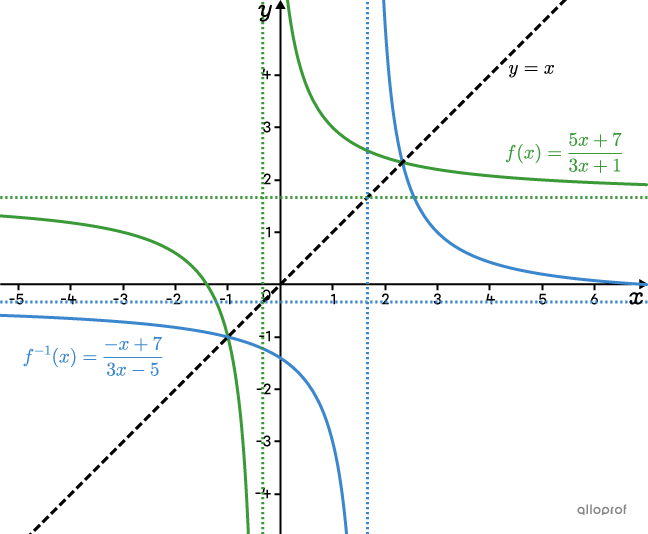
Answer: The inverse of |\color{#3a9a38}{f(x)= \dfrac{5x+7}{3x+1}}| is |\color{#3B87CD}{f^{-1}(x)=\dfrac{-x + 7}{3x-5}}.|
The following graph indicates |\color{#3a9a38}{f(x)}| and |\color{#3B87CD}{f^{-1}(x)}.|
The inverse of a function can be graphed by inverting the |x| and |y| coordinates of certain points.
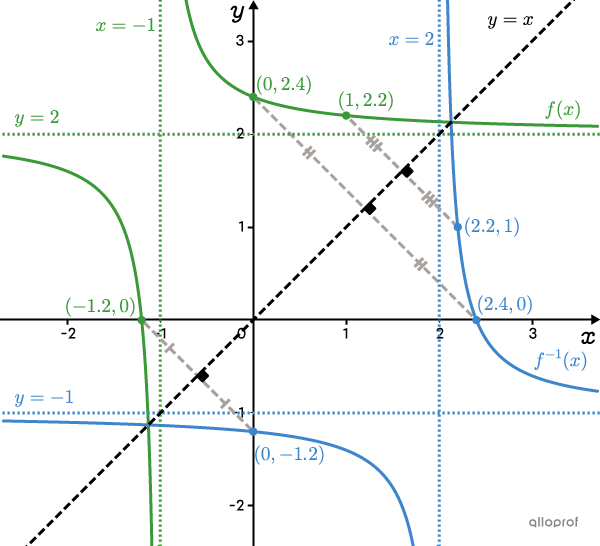
For example, in the following graph, observe the function |\color{#3a9a38}{f(x)=\dfrac{2}{5(x+1)}+2}| and its inverse, |\color{#3B87CD}{f^{-1}(x)=\dfrac{2}{5(x-2)}-1}.|
-
The |y|-intercept of |\color{#3a9a38}{f(x)}| becomes the |x|-intercept of |\color{#3B87CD}{f^{-1}(x)}.|
||\color{#3a9a38}{(0,2.4)}\ \rightarrow\ \color{#3B87CD}{(2.4,0)}|| -
The |x|-intercept of |\color{#3a9a38}{f(x)}| becomes the |y|-intercept of |\color{#3B87CD}{f^{-1}(x)}.|
||\color{#3a9a38}{(-1.2,0)}\ \rightarrow\ \color{#3B87CD}{(0,-1.2)}|| -
Point |\color{#3a9a38}{(1.2,2)}| becomes point |\color{#3B87CD}{(2.2,1)}| and so on.
The same is true for the asymptotes. The vertical asymptote of |\color{#3a9a38}{f(x)}| becomes the horizontal asymptote of |\color{#3B87CD}{f^{-1}(x)}| and vice versa.
||\begin{align} &\color{#3a9a38}{x=-1}\ &&\rightarrow\ &&\color{#3B87CD}{y=-1}\\ &\color{#3a9a38}{y=2}\ &&\rightarrow\ &&\color{#3B87CD}{x=2} \end{align}||
In addition, |\color{#3B87CD}{f^{-1}(x)}| corresponds to the reflection of |\color{#3a9a38}{f(x)}| with respect to the line |y=x.| Therefore, it is possible to graph the inverse using a reflection, provided that the scale of axes |x| and |y| have a ratio of |1:1.|