Le rapport sinus est l’un des 3 principaux rapports trigonométriques que l'on retrouve dans un triangle rectangle.
Dans un triangle rectangle, le sinus d’un angle |(\boldsymbol \theta)| correspond au rapport entre la mesure de la cathète opposée à l’angle et la mesure de l’hypoténuse.||\sin \theta=\dfrac{\text{cathète $\color{#EC0000}{\text{opposée}}$ à l'angle }\theta}{\text{$\color{#3A9A38}{\text{hypoténuse}}$}}||
Ainsi, si on veut déterminer le sinus des angles aigus dans le triangle rectangle suivant, on obtient 2 rapports.
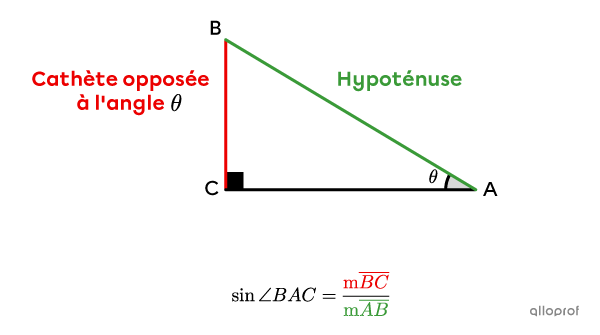
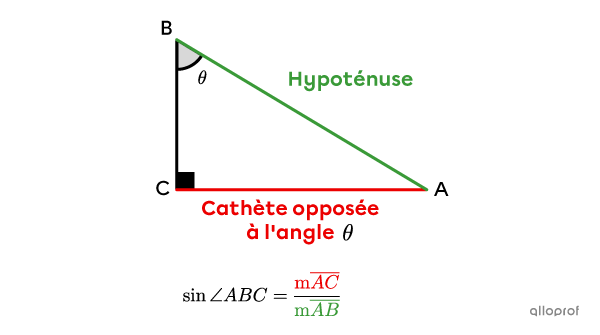
Le rapport trigonométrique sinus ne s’utilise qu’avec les angles aigus d’un triangle rectangle. Ainsi, on ne cherche jamais le sinus à partir de l’angle droit.
Pour déterminer la mesure d’une cathète dans un triangle rectangle à l’aide du rapport sinus, on doit connaitre la mesure de l’hypoténuse et celle de l’angle opposé au côté recherché.
Détermine la mesure du côté |\overline{BC}| à l’aide du rapport sinus dans le triangle rectangle suivant.

On doit choisir l’angle à utiliser pour déterminer la mesure de |\overline{BC}| à l’aide du rapport sinus.
Comme le côté |\overline{BC}| est adjacent à l’angle de |56^{\circ}| et non opposé à ce dernier, on ne peut pas utiliser le rapport sinus à partir de cet angle.
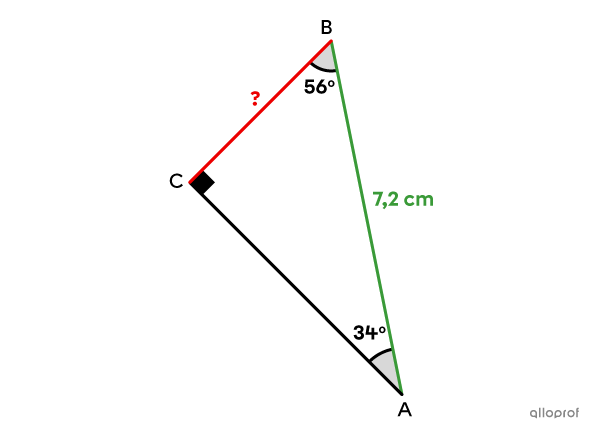
Le côté |\overline{BC}| est opposé à l’angle de |34^{\circ}.| Comme on connait également la mesure de l’hypoténuse, on peut utiliser le rapport sinus avec un angle |\theta| de |34^{\circ}| pour déterminer la mesure du côté |\overline{BC}.|
On substitue les mesures dans le rapport.||\begin{align}\sin \theta&=\dfrac{\text{cathète $\color{#EC0000}{\text{opposée}}$ à l'angle }\theta}{\text{$\color{#3A9A38}{\text{hypoténuse}}$}}\\\sin34^{\circ}&=\dfrac{\color{#EC0000}{\text{m}\overline{BC}}}{\color{#3A9A38}{7{,}2}}\end{align}||À l’aide de la calculatrice, on calcule le sinus de |34^{\circ}| et on isole la mesure recherchée.||\begin{align}0{,}559\,2&\approx\dfrac{\color{#EC0000}{\text{m}\overline{BC}}}{\color{#3A9A38}{7{,}2}}\\4{,}026\,2&\approx\color{#EC0000}{\text{m}\overline{BC}}\end{align}||
Réponse : Arrondie au centième près, la mesure du côté |\overline{BC}| est d’environ |4{,}03\ \text{cm}.|
Pour plus de précision, il est préférable d’effectuer le calcul en une seule étape sur la calculatrice. Si ce n’est pas possible, il est avantageux de conserver un minimum de 3 à 4 chiffres après la virgule.
Voici un exemple lorsque |\theta=65^{\circ}| et que l’hypoténuse mesure |59\ \text{cm}.|
En effectuant le calcul en 1 seule étape
|\begin{align}\sin65^{\circ}&=\dfrac{a}{{59}}\\\sin65^{\circ}\times59&=a\\\color{#EC0000}{53{,}47}&\approx a\end{align}|
En effectuant le calcul en 2 étapes
|\begin{align}\sin65^{\circ}&=\dfrac{a}{59}\\\color{#ec0000}{0{,}91}&\approx\dfrac{a}{59}\\0{,}91\times59&\approx a\\\color{#EC0000}{53{,}69}&\approx a\end{align}|
En effectuant le calcul en 2 étapes et en ne conservant que 2 décimales lors du calcul du sinus de l’angle, on obtient une différence de 22 centièmes avec la réponse attendue.
Dans certains cas, ni la mesure du côté opposé à l’angle ni celle de l'hypoténuse sont connues. Pour pouvoir appliquer le rapport sinus, il faut alors déterminer la mesure de l’autre angle.
Détermine la mesure de la cathète recherchée à l’aide du rapport sinus dans le triangle rectangle suivant.
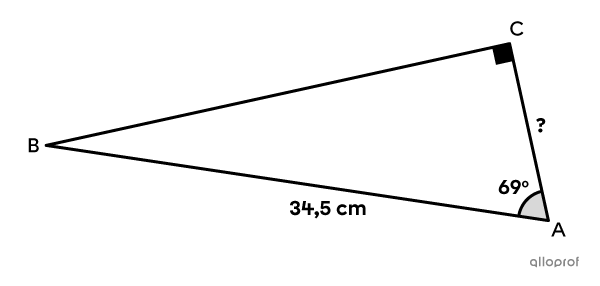
On doit choisir l’angle à utiliser pour déterminer la mesure du côté recherché à l’aide du rapport sinus.
Comme le côté |\overline{AC}| est adjacent à l’angle de |69^{\circ}| et non opposé à ce dernier, on ne peut pas utiliser le rapport sinus à partir de cet angle.
On doit alors déterminer la mesure de l’autre angle.||\begin{align}180^{\circ}-90^{\circ}-69^{\circ}&=\text{m}\angle ABC\\21^{\circ}&=\text{m}\angle ABC\end{align}||
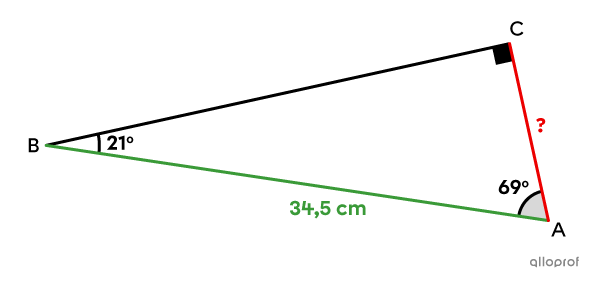
Le côté |\overline{AC}| est opposé à l’angle de |21^{\circ}.| Comme on connait également la mesure de l’hypoténuse, on peut utiliser le rapport sinus avec un angle |\theta| de |21^{\circ}.|||\begin{align}\sin \theta&=\dfrac{\text{cathète $\color{#EC0000}{\text{opposée}}$ à l'angle }\theta}{\text{$\color{#3A9A38}{\text{hypoténuse}}$}}\\\sin21^{\circ}&=\dfrac{\color{#EC0000}{\text{m}\overline{AC}}}{\color{#3A9A38}{34{,}5}}\\\sin21^{\circ}\times \color{#3A9A38}{34{,}5}&=\color{#EC0000}{\text{m}\overline{AC}}\\12{,}36&\approx\color{#EC0000}{\text{m}\overline{AC}}\end{align}||
Réponse : La mesure de la cathète recherchée est d’environ |12{,}36\ \text{cm}.|
Dans l’exemple précédent, il aurait été possible d’utiliser le rapport trigonométrique cosinus pour déterminer la mesure de la cathète recherchée à l’aide de l’angle de |69^{\circ}.| La réponse aurait alors été la même.
Pour déterminer la mesure de l’hypoténuse dans un triangle rectangle à l’aide du rapport sinus, on doit connaitre la mesure d’un angle aigu et celle de son côté opposé.
Détermine la mesure de l’hypoténuse à l’aide du rapport sinus dans le triangle rectangle suivant.

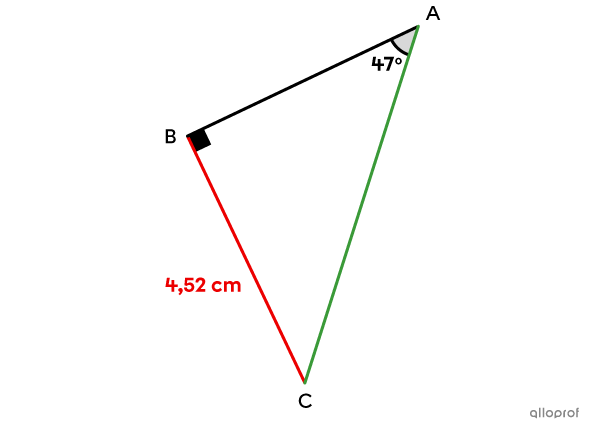
Le côté |\overline{BC}| est opposé à l’angle de |47^{\circ}.| Comme on cherche la mesure de l’hypoténuse, on peut utiliser le rapport sinus avec un angle |\theta| de |47^{\circ}.|||\begin{align}\sin \theta&=\dfrac{\text{cathète $\color{#EC0000}{\text{opposée}}$ à l'angle }\theta}{\text{$\color{#3A9A38}{\text{hypoténuse}}$}}\\\sin47^{\circ}&=\dfrac{\color{#EC0000}{4{,}52}}{\color{#3A9A38}{\text{m}\overline{AC}}}\end{align}||Puisque la mesure de l’hypoténuse se trouve au dénominateur dans le rapport, on peut procéder de la façon suivante.||\begin{align}\dfrac{\sin47^{\circ}}{1}&=\dfrac{4{,}52}{\color{#3A9A38}{\text{m}\overline{AC}}}\\\color{#3A9A38}{\text{m}\overline{AC}}\times\sin47^{\circ} &=4{,}52\times 1\\\color{#3A9A38}{\text{m}\overline{AC}}&=\dfrac{4{,}52}{\sin47^{\circ}}\\\color{#3A9A38}{\text{m}\overline{AC}}&\approx 6{,}18\end{align}||
Réponse : La mesure de l’hypoténuse est d’environ |6{,}18\ \text{cm}.|
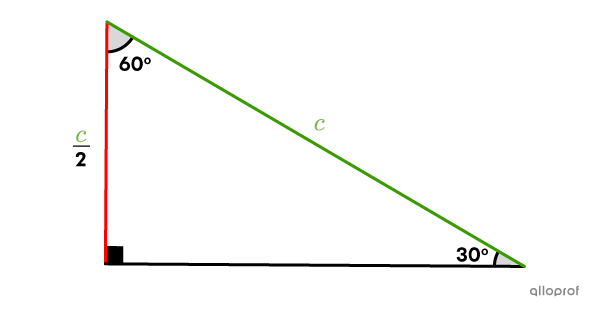
Dans un triangle rectangle, la mesure de la cathète opposée à l'angle de |30^{\circ}| est toujours égale à la moitié de celle de l'hypoténuse.
Le rapport sinus est donc toujours de |\dfrac{1}{2}.|||\begin{align}\sin30^{\circ}&=\dfrac{\text{cathète $\color{#EC0000}{\text{opposée}}$ à l'angle }\theta}{\text{$\color{#3A9A38}{\text{hypoténuse}}$}}\\&=\dfrac{\frac{\color{#3A9A38}c}{2}}{\color{#3A9A38}c}\\&=\dfrac{1}{2}\end{align}||
Quelle est la mesure du côté |\overline{AB}| dans le triangle suivant?

Comme le triangle rectangle comporte un angle de |30^{\circ},| on sait que la mesure du côté qui lui est opposé vaut la moitié de celle de l’hypoténuse. La mesure de l’hypoténuse est donc le double de |4{,}5.|
||\overline{AB}=4{,}5\times 2=9\ \text{cm}||
Réponse : La mesure du côté |\overline{AB}| est de |9\ \text{cm}.|
Pour déterminer la mesure d’un angle aigu dans un triangle rectangle à l’aide du rapport sinus, on doit connaitre la mesure de son côté opposé et celle de l’hypoténuse. Cela revient à répondre à la question suivante : « Quel angle me donne un sinus de…? »
On détermine d’abord le rapport sinus, puis on utilise la touche |\sin^{-1}| (qu’on appelle aussi |arcsin|) sur la calculatrice.
Détermine la mesure de l’angle |BAC| dans le triangle rectangle suivant à l’aide du rapport sinus.
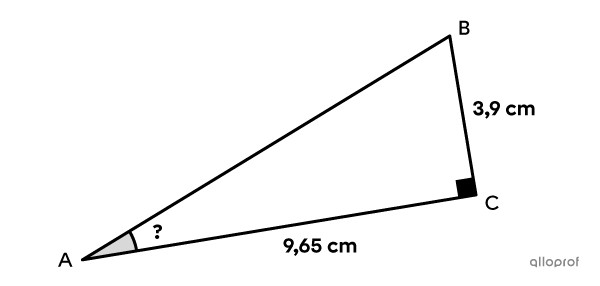
On connait uniquement la mesure du côté qui est opposé à l’angle |BAC| et celle du côté qui lui est adjacent. On ne peut donc pas appliquer le rapport sinus. Il faut avant tout déterminer la mesure de l’hypoténuse. Comme on connait les 2 cathètes du triangle, on peut appliquer le théorème de Pythagore afin de déterminer sa mesure.||\begin{align}\left(\text{m}\overline{AC}\right)^2+\left(\text{m}\overline{BC}\right)^2&=\left(\text{m}\overline{AB}\right)^2\\9{,}65^2+3{,}9^2&=\left(\text{m}\overline{AB}\right)^2\\\color{#EC0000}{\sqrt{\color{black}{108{,}332\,5}}}&=\color{#EC0000}{\sqrt{\color{black}{\left(\text{m}\overline{AB}\right)^2}}}\\10{,}41&\approx \text{m}\overline{AB}\end{align}||La mesure de l’hypoténuse est donc d’environ |10{,}41\ \text{cm}.| On peut maintenant appliquer le rapport sinus pour déterminer la mesure de l’angle |BAC.|||\begin{align}\sin \theta &=\dfrac{\text{cathète $\color{#EC0000}{\text{opposée}}$ à l'angle }\theta}{\text{$\color{#3A9A38}{\text{hypoténuse}}$}}\\\sin \theta&=\dfrac{\color{#EC0000}{3{,}9}}{\color{#3A9A38}{10{,}41}}\\\theta&=\color{#EC0000}{\sin^{-1}\left(\color{black}{\dfrac{3{,}9}{10{,}41}}\right)}\\\theta&\approx22^{\circ}\end{align}||
Réponse : La mesure de l’angle |BAC| est d’environ |22^{\circ}.|
En trigonométrie, plusieurs démarches sont possibles pour arriver au même résultat. Dans l’exemple précédent, on aurait pu utiliser |\boldsymbol{\tan^{-1}}| à partir de l’angle |BAC,| ce qui aurait donné sa mesure.
Voici une partie de ce qu’on appelle une table trigonométrique, un outil qui était utilisé en mathématiques avant l’invention de la calculatrice. On y a inscrit la mesure de certains angles et le rapport sinus qui leur est associé.
À l’époque, on devait utiliser ce tableau pour trouver la mesure d’un angle dans un triangle rectangle. Par exemple, si on savait qu’un rapport sinus valait environ |0{,}642\,8,| alors l’angle cherché était de |40^{\circ}.|
Heureusement, depuis l’invention de la calculatrice, il n’est plus obligatoire d'utiliser la table trigonométrique pour déterminer un angle dans un triangle rectangle.
| Mesure de l’angle | Rapport sinus |
|---|---|
| |10^{\circ}| | |\approx 0{,}173\,6| |
| |20^{\circ}| | |\approx 0{,}342\,0| |
| |30^{\circ}| | |0{,}5| |
| |40^{\circ}| | |\approx 0{,}642\,8| |
| |50^{\circ}| | |\approx 0{,}766\,0| |
| |60^{\circ}| | |\approx 0{,}866\,0| |
Heureusement, depuis l’invention de la calculatrice, il n’est plus obligatoire d'utiliser la table trigonométrique pour déterminer un angle dans un triangle rectangle.
La fonction arc sinus, notée |\sin^{-1}(x),| est la réciproque de la fonction sinus.||\sin \theta=x\ \Leftrightarrow \ \sin^{-1}x=\theta||