The sine ratio is one of the 3 main trigonometric ratios found in a right triangle.
In a right triangle, the sine of an angle |(\boldsymbol \theta)| is the ratio between the length of the leg that is opposite the angle and the hypotenuse.||\sin \theta=\dfrac{\text{leg $\color{#EC0000}{\text{opposite}}$ angle }\theta}{\text{$\color{#3A9A38}{\text{hypotenuse}}$}}||
If we want to find the sine of the acute angles in the following right triangle, we get 2 ratios.
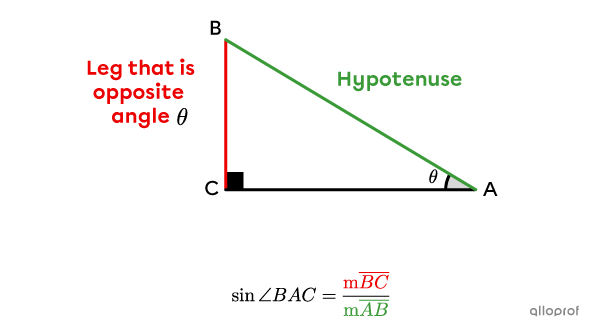
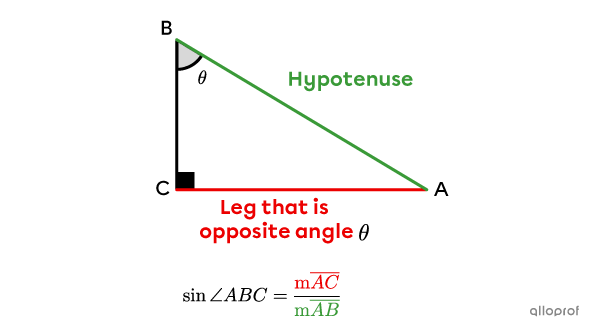
The sine trigonometric ratio is only used with respect to the acute angles of a right triangle. The sine is never sought in relation to the right angle.
To find the length of a leg of a right triangle using the sine ratio, the length of the hypotenuse and the measure of the angle opposite the side in question must be known.
Find the length of side |\overline{BC}| using the sine ratio in the following right triangle.

Choose which angle to use to determine the length of |\overline{BC}| directly using the sine ratio.
Since side |\overline{BC}| is adjacent to the |56^{\circ}| angle and not opposite it, the sine ratio cannot be used with respect to this angle.
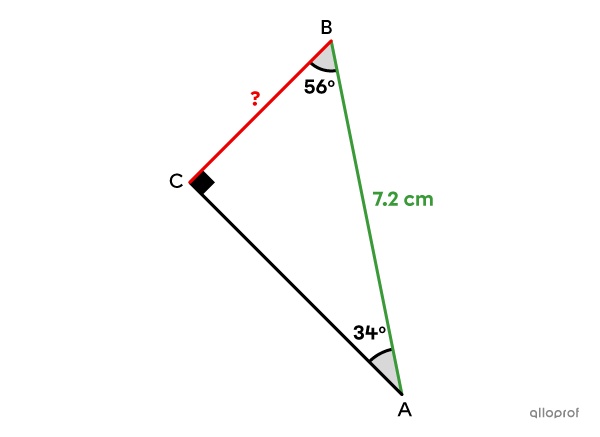
Side |\overline{BC}| is opposite the |34^{\circ}| angle. Since the length of the hypotenuse is also known, we can use the sine ratio with respect to the angle |\theta| of |34^{\circ}| to find the measure of side |\overline{BC}.|
Substitute the measurements into the ratio.||\begin{align}\sin \theta&=\dfrac{\text{leg $\color{#EC0000}{\text{opposite}}$ the angle }\theta}{\text{$\color{#3A9A38}{\text{hypotenuse}}$}}\\\sin34^{\circ}&=\dfrac{\color{#EC0000}{\text{m}\overline{BC}}}{\color{#3A9A38}{7.2}}\end{align}||Using a calculator, calculate the sine of |34^{\circ}| and isolate the desired measurement.||\begin{align}0.5592&\approx\dfrac{\color{#EC0000}{\text{m}\overline{BC}}}{\color{#3A9A38}{7.2}}\\4.0262&\approx\color{#EC0000}{\text{m}\overline{BC}}\end{align}||
Answer: Rounded to the nearest hundredth, side |\overline{BC}| measures approximately |4.03\ \text{cm}.|
For greater accuracy, do the calculations in one step on a calculator. If this is not possible, keep at least 3 to 4 digits after the decimal point to ensure greater accuracy.
Here is an example when |\theta=65^{\circ}| and the hypotenuse measures |59\ \text{cm}.|
Performing the calculation in one step
|\begin{align}\sin65^{\circ}&=\dfrac{a}{{59}}\\\sin65^{\circ}\times59&=a\\\color{#EC0000}{53.47}&\approx a\end{align}|
Performing the calculation in 2 steps
|\begin{align}\sin65^{\circ}&=\dfrac{a}{59}\\\color{#ec0000}{0.91}&\approx\dfrac{a}{59}\\0.91\times59&\approx a\\\color{#EC0000}{53.69}&\approx a\end{align}|
If the calculations are performed in 2 steps, and we only round to 2 decimal places when calculating the sine of the angle, there will be a difference of 22 hundredths compared to the correct answer.
In some cases, neither the length of the hypotenuse nor the length of the side opposite the angle are known. In order to apply the sine ratio, the measure of the other angle has to be determined.
Use the sine ratio to determine the length of the leg sought in the following right triangle.
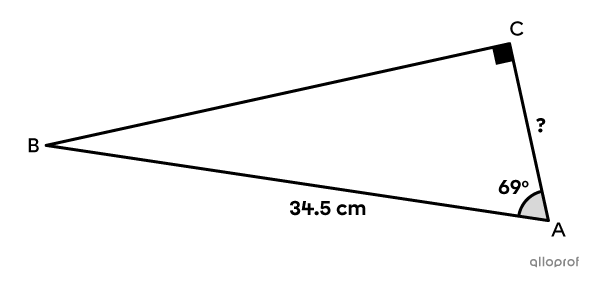
Choose the angle to use to apply the sine ratio in order to find the side measurement sought.
Since side |\overline{AC}| is adjacent to the |69^{\circ}| angle and not opposite it, the sine ratio cannot be used with respect to this angle.
Therefore, the measure of the other angle must be found.||\begin{align}180^{\circ}-90^{\circ}-69^{\circ}&=\text{m}\angle ABC\\21^{\circ}&=\text{m}\angle ABC\end{align}||
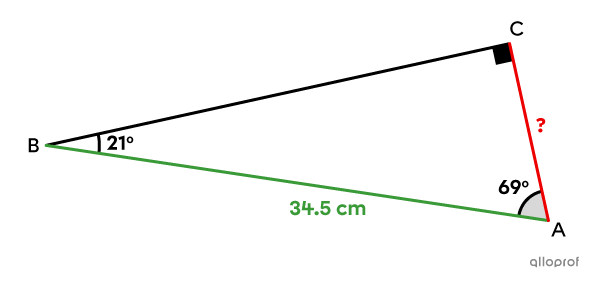
Side |\overline{AC}| is opposite the |21^{\circ}| angle. Since the length of the hypotenuse is also known, the sine ratio can be used with respect to angle |\theta| of |21^{\circ}.|
||\begin{align}\sin \theta&=\dfrac{\text{leg $\color{#EC0000}{\text{opposite}}$ angle }\theta}{\text{$\color{#3A9A38}{\text{hypotenuse}}$}}\\\sin21^{\circ}&=\dfrac{\color{#EC0000}{\text{m}\overline{AC}}}{\color{#3A9A38}{34.5}}\\\sin21^{\circ}\times \color{#3A9A38}{34.5}&=\color{#EC0000}{\text{m}\overline{AC}}\\12.36&\approx\color{#EC0000}{\text{m}\overline{AC}}\end{align}||
Answer: The leg sought measures approximately |12.36\ \text{cm}.|
In the last example, the cosine trigonometric ratio could have been used to find the length of the leg sought using the |69^{\circ}| angle. The answer would be the same.
To find the length of the hypotenuse in a right triangle using the sine ratio, the measure of one acute angle and the side opposite it must be known.
Find the length of the hypotenuse using the sine ratio in the following right triangle.

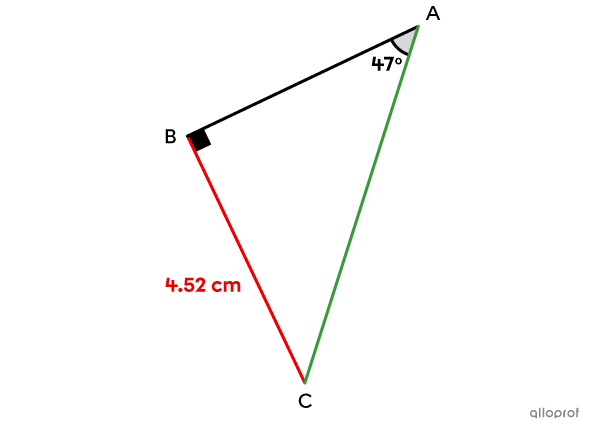
Side |\overline{BC}| is opposite the |47^{\circ}| angle. Since we want to find the length of the hypotenuse, we can use the sine ratio with angle |\theta| of |47^{\circ}.|||\begin{align}\sin \theta&=\dfrac{\text{leg $\color{#EC0000}{\text{opposite}}$ angle }\theta}{\text{$\color{#3A9A38}{\text{hypotenuse}}$}}\\\sin47^{\circ}&=\dfrac{\color{#EC0000}{4.52}}{\color{#3A9A38}{\text{m}\overline{AC}}}\end{align}||Since the length of the hypotenuse is found in the denominator of the ratio, proceed as follows:||\begin{align}\dfrac{\sin47^{\circ}}{1}&=\dfrac{4.52}{\color{#3A9A38}{\text{m}\overline{AC}}}\\\color{#3A9A38}{\text{m}\overline{AC}}\times\sin47^{\circ} &=4.52\times 1\\\color{#3A9A38}{\text{m}\overline{AC}}&=\dfrac{4.52}{\sin47^{\circ}}\\\color{#3A9A38}{\text{m}\overline{AC}}&\approx 6.18\end{align}||
Answer: The hypotenuse measures approximately |6.18\ \text{cm}.|
In a right triangle, the length of the leg opposite a |30^{\circ}| angle is always equal to half the length of the hypotenuse.
This means the sine ratio is always |\dfrac{1}{2}.|||\begin{align}\sin30^{\circ}&=\dfrac{\text{leg $\color{#EC0000}{\text{opposite}}$ angle }\theta}{\text{$\color{#3A9A38}{\text{hypotenuse}}$}}\\&=\dfrac{\frac{\color{#3A9A38}c}{2}}{\color{#3A9A38}c}\\&=\dfrac{1}{2}\end{align}||
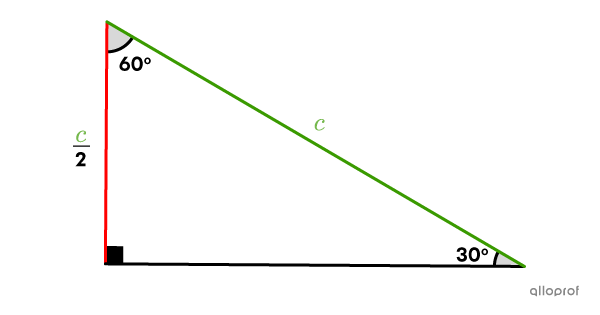
What is the length of side |\overline{AB}| in the following triangle?

Since the right triangle has a |30^{\circ}| angle, we know the length of the side opposite it is half the length of the hypotenuse. Therefore, the hypotenuse measures 2 times |4.5.|||\overline{AB}=4.5\times 2=9\ \text{cm}||Answer: Side |\overline{AB}| measures |9\ \text{cm}.|
To find the measure of an acute angle in a right triangle using the sine ratio, the length of the side opposite it and the length of the hypotenuse must be known. This is essentially the same as answering the following question: “What angle gives a sine of...?”
First, determine the sine ratio, then use the |\sin^{-1}| key (also called |arcsin| ) on a calculator.
Find the measure of angle |BAC| in the following right triangle using the sine ratio.
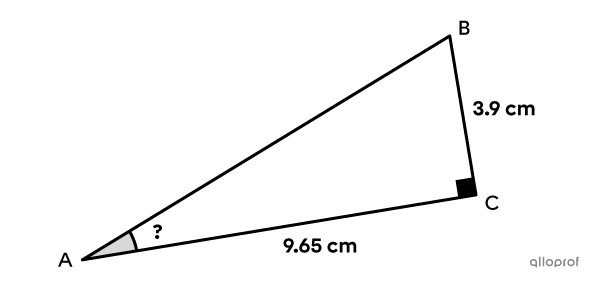
The only given information is the length of the side opposite angle |BAC| and the length of the side adjacent to it. This means the sine ratio cannot be applied. The length of the hypotenuse must be determined first. Since the 2 legs of the right triangle are known, the Pythagorean theorem can be applied to find this length.||\begin{align}\left(\text{m}\overline{AC}\right)^2+\left(\text{m}\overline{BC}\right)^2&=\left(\text{m}\overline{AB}\right)^2\\9.65^2+3.9^2&=\left(\text{m}\overline{AB}\right)^2\\\color{#EC0000}{\sqrt{\color{black}{108.3325}}}&=\color{#EC0000}{\sqrt{\color{black}{\left(\text{m}\overline{AB}\right)^2}}}\\10.41&\approx \text{m}\overline{AB}\end{align}||The hypotenuse measures approximately |10.41\ \text{cm}.| The sine ratio can now be applied to find the measure of angle |BAC.|||\begin{align}\sin \theta &=\dfrac{\text{leg $\color{#EC0000}{\text{opposite}}$ angle }\theta}{\text{$\color{#3A9A38}{\text{hypotenuse}}$}}\\\sin \theta&=\dfrac{\color{#EC0000}{3.9}}{\color{#3A9A38}{10.41}}\\\theta&=\color{#EC0000}{\sin^{-1}\left(\color{black}{\dfrac{3.9}{10.41}}\right)}\\\theta&\approx22^{\circ}\end{align}||Answer: Angle |BAC| measures approximately |22^{\circ}.|
In trigonometry, there are several possible ways to get the same answer. In the previous example, we could have used |\boldsymbol{\tan^{-1}}| with respect to angle |BAC,| which would have given the measurement directly.
Here is part of a trigonometric table, which is a tool used in mathematics before the invention of the calculator. It includes the measures of certain angles and their corresponding sine ratios.
At that time, this table had to be used to find an angle measure in a right triangle. For example, if it was calculated that the sine ratio was |0.6428,| then the angle sought would measure |40^{\circ}.|
| Angle measure | Sine ratio |
|---|---|
| |10^{\circ}| | |\approx 0.1736| |
| |20^{\circ}| | |\approx 0.342| |
| |30^{\circ}| | |0.5| |
| |40^{\circ}| | |\approx 0.6428| |
| |50^{\circ}| | |\approx 0.766| |
| |60^{\circ}| | |\approx 0.866| |
Thankfully, since calculators were invented, we no longer need to use the trigonometric table to determine the measure of an angle in a right triangle.
The arcsine function (denoted |\sin^{-1}(x)| ) is the inverse of the sine function.||\sin \theta=x\ \Leftrightarrow \ \sin^{-1}x=\theta||