Cette MiniRécup porte sur les nuages de points, la corrélation et les droites de régression. Ses vidéos interactives, son résumé et son exercice récapitulatif te permettront de réviser ces notions.
Pour tracer un nuage de points, tu dois être en mesure de placer des points dans un plan cartésien. Tu dois savoir comment associer un nuage de points à un modèle mathématique, c’est-à-dire à une famille de fonctions. En particulier, il est important de connaitre les fonctions polynomiales de degré 0 et 1 (affines et linéaires) et la fonction de variation inverse. Tu dois notamment être capable de trouver la règle d’une fonction affine.
Finalement, comme les méthodes pour trouver des droites de régression reposent sur les concepts de la moyenne et de la médiane, tu dois être capable de trouver ces mesures de tendance centrale dans une distribution de données.
Une distribution à 2 variables peut être représentée à l’aide d’un nuage de points. Par la suite, on tente de déterminer s’il y a un lien, c’est-à-dire une corrélation entre les 2 variables.
La corrélation en question peut être linéaire ou non. L’important est de trouver le modèle mathématique qui représente le mieux le nuage de points étudié. C’est ce qu’on appelle faire de la modélisation.
Lorsque le nuage de points semble former une courbe particulière, on parle alors de courbe de tendance et on peut le modéliser à l’aide de différentes fonctions, dont la fonction de variation inverse.
Lorsque le nuage de points semble plutôt former une ligne droite, on parle de corrélation linéaire et on modélise les données à l’aide d’une droite de régression, soit une fonction affine |(y=ax+b).|
Le coefficient de corrélation linéaire |\boldsymbol{(r)}|
On peut étudier la force de la corrélation d’une distribution en calculant le coefficient de corrélation linéaire. Ce dernier varie entre |-1| et |1.|
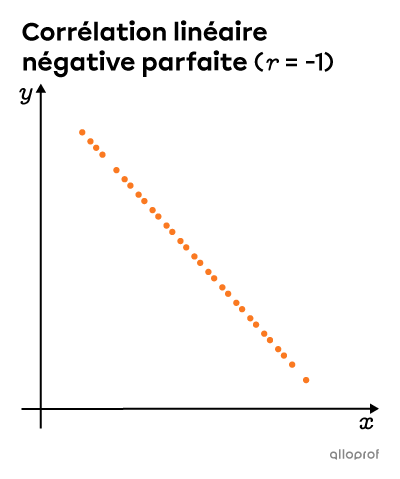

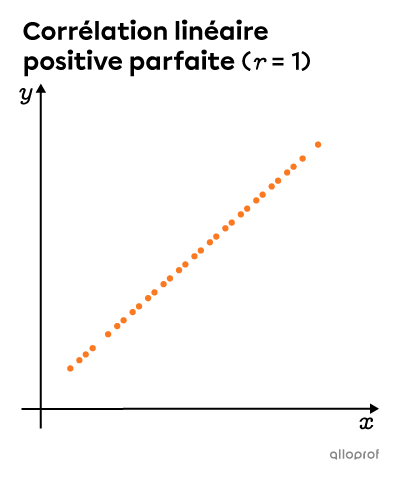
Pour calculer |r| de façon précise, on peut utiliser les outils technologiques. Pour une valeur approximative, on trace un rectangle autour du nuage de points, on mesure la largeur et la longueur de ce rectangle, puis on utilise la formule suivante.||r\approx\pm\left(1-\dfrac{\text{petit côté}}{\text{grand côté}}\right)||
Les méthodes pour trouver la règle d’une droite de régression et faire des prédictions
Si la corrélation linéaire entre 2 variables est forte, on peut utiliser les données pour faire des prédictions. Pour cela, il faut d’abord trouver la règle de la droite de régression. Pour y arriver, plusieurs méthodes sont possibles. Voici les étapes à effectuer pour chacune de ces méthodes.
La méthode graphique
-
Placer les points dans un plan cartésien.
-
Tracer une droite de régression.
-
Déterminer 2 points situés sur la droite de régression.
-
Trouver la règle de la droite à l’aide de ces 2 points.
-
Prédire une valeur à l’aide de la règle.
La droite de Mayer
-
Ordonner les coordonnées selon la variable indépendante.
-
Séparer la distribution en 2 groupes égaux, si possible.
-
Calculer les points moyens de chaque groupe |(P_1| et |P_2).|
-
Trouver la règle de la droite de régression passant par les points |P_1| et |P_2.|
-
Prédire des valeurs à l’aide de la règle de la droite.
La droite médiane-médiane
-
Ordonner les coordonnées selon la variable indépendante.
-
Séparer la distribution en 3 groupes égaux, si possible.
-
Calculer les points médians de chaque groupe |(M_1,| |M_2| et |M3).|
-
Calculer le point moyen |P,| dont les coordonnées sont la moyenne des abscisses et la moyenne des ordonnées des points médians.
-
Déterminer le taux de variation |(a)| de la droite passant par |M_1| et |M_3.|
-
Déterminer l’ordonnée à l’origine |(b)| de la droite passant par |P| et dont le taux de variation est |a.|
-
Prédire des valeurs à l’aide de la règle de la droite.
Faire une prédiction consiste à déterminer la valeur d’une variable lorsque la valeur de l’autre variable est connue.
-
Si la valeur connue est située à l’intérieur de l’intervalle couvert par le nuage de points, on parle d’interpolation.
-
Si la valeur connue est située à l’extérieur de l’intervalle couvert par le nuage de points, on parle d’extrapolation.
La fiabilité des prédictions et des méthodes
Plus la corrélation entre 2 variables d’une distribution est forte |(\vert r\vert| près de |1),| plus les prédictions seront fiables, et ce, peu importe la méthode choisie.
Voici les facteurs qui peuvent nuire à la fiabilité des prédictions.
-
L’échantillon est trop petit
En effet, on ne peut pas être sûr que notre modèle mathématique sera fiable à partir de seulement quelques données recueillies. -
La distribution comprend une ou des données éloignées
Les données éloignées ont une grande influence sur le calcul de la moyenne. Pour cette raison, il faut privilégier la méthode de la droite médiane-médiane lorsqu’on observe de telles données.