L’étude des vecteurs fait appel à de nombreuses notions de géométrie et de trigonométrie vues au cours des années précédentes.
En effet, pour calculer les composantes d’un vecteur, tu dois savoir utiliser les rapports trigonométriques dans le triangle rectangle. Pour calculer la norme d’un vecteur, tu peux utiliser le théorème de Pythagore ou la formule de distance entre deux points. Finalement, pour faire la somme ou la différence de vecteurs, tu pourrais avoir à utiliser la loi des sinus et la loi des cosinus. Il serait donc utile de réviser ces notions avant d’écouter les vidéos de cette MiniRécup.
Avant d’effectuer les opérations sur les vecteurs, il faut connaitre le vocabulaire qui s’y rattache :
-
Un scalaire est une quantité définie par un nombre réel, tandis qu’un vecteur est défini par un nombre ET une orientation.
-
La norme d’un vecteur |\overrightarrow{v},| notée |{\parallel}\overrightarrow{v}{\parallel}|, est sa longueur.
-
L’orientation d’un vecteur |(\theta_{\overrightarrow{v}})| fait référence à sa direction (la droite qui supporte le vecteur) et à son sens (indiqué par la pointe de la flèche). L’orientation est un angle mesuré dans le sens antihoraire à partir de l’axe des |x| positif.
-
Les composantes |(a,b)| d’un vecteur représentent le déplacement horizontal |(a)| et vertical |(b)| qu’il faut effectuer pour passer de l’origine du vecteur à son extrémité.
-
Deux vecteurs sont équipollents s’ils ont la même norme et la même orientation.
-
Deux vecteurs sont opposés s’ils ont la même norme et la même direction mais sont de sens opposé.
-
Deux vecteurs sont colinéaires s’ils ont la même direction. Autrement dit, ils sont parallèles.
-
Deux vecteurs sont orthogonaux s’ils sont perpendiculaires.
Avec la norme d’un vecteur |({\parallel}\overrightarrow{v}{\parallel})| et son orientation |(\theta_{\overrightarrow{v}})|, on peut calculer ses composantes |(a,b):| ||a = {\parallel}\overrightarrow{v}{\parallel} \cos \theta_{\overrightarrow{v}} \\ b={\parallel}\overrightarrow{v}{\parallel} \sin \theta_{\overrightarrow{v}}||
Avec les composantes d’un vecteur, on peut tracer un triangle rectangle, puis calculer sa norme à l’aide du théorème de Pythagore et son orientation à l’aide d’un rapport tangente.
Pour faire les différentes opérations sur les vecteurs (addition, soustraction, produit scalaire, etc.), il est préférable de travailler avec les composantes.
L’addition de vecteurs : on additionne les composantes horizontales entre elles, puis on fait de même pour les composantes verticales.
Exemple : ||\begin{align}(3,-5) + (6,2) &= (3+6, -5+2) \\ &= (9, -3)\end{align}||
La soustraction de vecteurs : on soustrait les composantes horizontales entre elles, puis on fait de même pour les composantes verticales.
Exemple : ||\begin{align}(3,-5) - (6,2) &= (3-6, -5-2) \\ &= (-3, -7)\end{align}||
La multiplication d’un vecteur par un scalaire : on distribue le scalaire à chaque composante du vecteur.
Exemple : ||\begin{align}5(2,-6) &= (5\times 2, 5\times -6) \\ &= (10,-30)\end{align}||Attention! Le résultat de la multiplication d’un vecteur par un scalaire est un vecteur.
Le produit scalaire : on additionne le produit des composantes horizontales avec le produit des composantes verticales.
Exemple : ||\begin{align} (-2,3)\cdot (5,4) &= -2\times 5 + 3 \times 4 \\ &= -10+12 \\ &=2 \end{align}||Attention! Le produit scalaire, qui est le produit de 2 vecteurs, donne un scalaire.
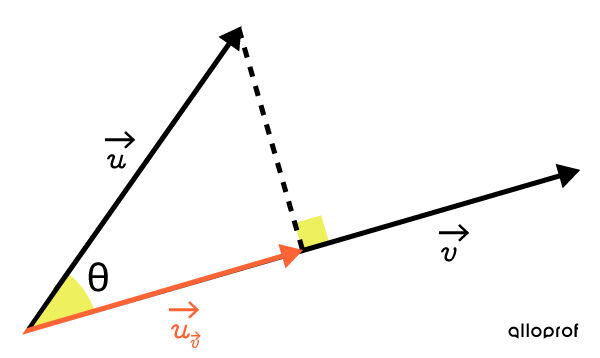
La projection orthogonale
Sur la figure ci-contre, la projection orthogonale de |\overrightarrow{u}| sur |\overrightarrow{v}| est le vecteur |\overrightarrow{u}_{\overrightarrow{v}}.|
Pour calculer la norme de cette projection orthogonale, on peut utiliser la formule suivante : ||{\parallel}\overrightarrow{u}_\overrightarrow{v}{\parallel} = {\parallel}\overrightarrow{u}{\parallel} \cos \theta||
où |\theta=| Angle aigu entre |\overrightarrow{u}| et |\overrightarrow{v}|
Pour calculer les composantes de cette projection orthogonale, on doit plutôt utiliser la formule suivante : ||\overrightarrow{u}_{\overrightarrow{v}}=\dfrac{\overrightarrow{u} \cdot \overrightarrow{v}}{\parallel \overrightarrow{v} \parallel^2} \overrightarrow{v}||
La combinaison linéaire (vue en SN seulement)
On peut combiner 2 vecteurs non parallèles pour former n’importe quel vecteur du plan cartésien. On peut représenter la combinaison linéaire à l’aide de l’égalité suivante : ||\overrightarrow{v}=a\overrightarrow{u_1}+b\overrightarrow{u_2}||
où |a| et |b| sont des scalaires, alors que |\overrightarrow{u_1}| et |\overrightarrow{u_2}| sont des vecteurs non parallèles qui forment une base vectorielle.
Pour trouver la valeur des coefficients |a| et |b,| il faut résoudre un système d’équations formé à partir des composantes en |x| et des composantes en |y.|