-
The perimeter, generally denoted |P,| is the length of the contour of a figure. In the case of the circle, the perimeter is called “circumference” and is denoted |C.|
-
The area, generally denoted |A,| is the surface delimited by a figure.
|
Plane Figure |
Perimeter |
Area |
|---|---|---|
 |
||P=\color{#3A9A38}{\boldsymbol{a}}+\color{#3B87CD}{\boldsymbol{b}}+\color{#FF55C3}{\boldsymbol{c}}|| |
||A=\dfrac{\color{#3B87CD}{\boldsymbol{b}}\times\color{#EC0000}{\boldsymbol{h}}}{2}|| |
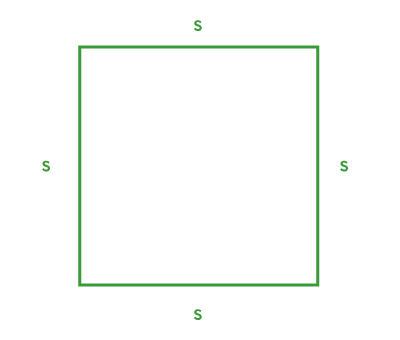 |
||\begin{align}P&=\color{#3A9A38}{\boldsymbol{s}}+\color{#3A9A38}{\boldsymbol{s}}+\color{#3A9A38}{\boldsymbol{s}}+\color{#3A9A38}{\boldsymbol{s}}\\&=4\color{#3A9A38}{\boldsymbol{s}}\end{align}|| |
||\begin{align}A&=\color{#3A9A38}{\boldsymbol{s}}\times\color{#3A9A38}{\boldsymbol{s}}\\&=\color{#3A9A38}{\boldsymbol{s}}^2\end{align}|| |
 |
||\begin{align}P&=\color{#3B87CD}{\boldsymbol{b}}+\color{#3B87CD}{\boldsymbol{b}}+\color{#EC0000}{\boldsymbol{h}}+\color{#EC0000}{\boldsymbol{h}}\\&=2\color{#3B87CD}{\boldsymbol{b}}+2\color{#EC0000}{\boldsymbol{h}}\\&=2(\color{#3B87CD}{\boldsymbol{b}}+\color{#EC0000}{\boldsymbol{h}})\end{align}|| |
||A=\color{#3B87CD}{\boldsymbol{b}}\times\color{#EC0000}{\boldsymbol{h}}|| |
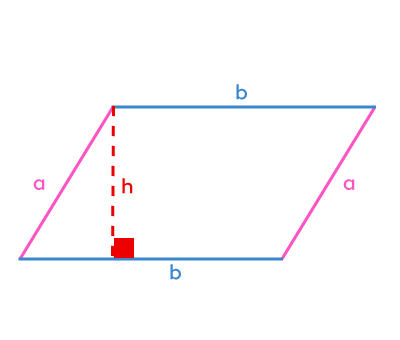 |
||\begin{align}P&=\color{#FF55C3}{\boldsymbol{a}}+\color{#FF55C3}{\boldsymbol{a}}+\color{#3B87CD}{\boldsymbol{b}}+\color{#3B87CD}{\boldsymbol{b}}\\&=2\color{#FF55C3}{\boldsymbol{a}}+2\color{#3B87CD}{\boldsymbol{b}}\\&=2(\color{#FF55C3}{\boldsymbol{a}}+\color{#3B87CD}{\boldsymbol{b}})\end{align}|| |
||A=\color{#3B87CD}{\boldsymbol{b}}\times\color{#EC0000}{\boldsymbol{h}}|| |
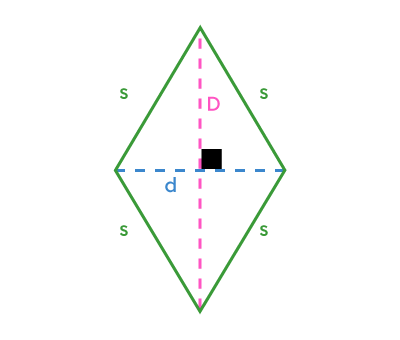 |
||\begin{align}P&=\color{#3A9A38}{\boldsymbol{s}}+\color{#3A9A38}{\boldsymbol{s}}+\color{#3A9A38}{\boldsymbol{s}}+\color{#3A9A38}{\boldsymbol{s}}\\&=4\color{#3A9A38}{\boldsymbol{s}}\end{align}|| |
||A=\dfrac{\color{#FF55C3}{\boldsymbol{D}}\times\color{#3B87CD}{\boldsymbol{d}}}{2}|| |
 |
||P=\color{#3B87CD}{\boldsymbol{b}}+\color{#3A9A38}{\boldsymbol{a}}+\color{#FA7921}{\boldsymbol{B}}+\color{#FF55C3}{\boldsymbol{c}}|| |
||A=\dfrac{(\color{#3B87CD}{\boldsymbol{b}}+\color{#FA7921}{\boldsymbol{B}})\times\color{#EC0000}{\boldsymbol{h}}}{2}|| |
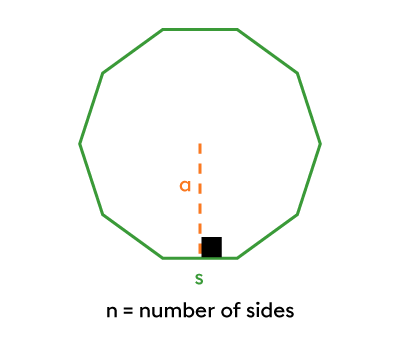 |
||P=n\times\color{#3A9A38}{\boldsymbol{s}}|| |
||A=\dfrac{\color{#3A9A38}{\boldsymbol{s}}\color{#FA7921}{\boldsymbol{a}}n}{2}|| |
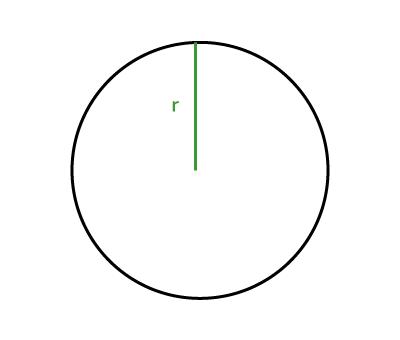 |
||C=2\pi\color{#3A9A38}{\boldsymbol{r}}|| |
||A=\pi\color{#3A9A38}{\boldsymbol{r}}^2|| |
-
The area of the base, generally denoted |A_b,| is the surface occupied by the figure(s) that serve as base for a solid.
-
The lateral area, generally denoted |A_L,| is the surface occupied by the figures that do not serve as base for a solid.
-
The total area, generally denoted |A_T,| is the surface occupied by all the figures forming a solid.
-
The volume, generally denoted |V,| is the space delimited by the faces of a solid.
|
Solid |
Area Formula |
Volume Formula |
|---|---|---|
|
Cube  |
Area of Cubes||\begin{align}A_b&=\color{#3a9a38}{\boldsymbol{s}}^2\\\\ A_L&=4\color{#3a9a38}{\boldsymbol{s}}^2\\\\A_T&=6\color{#3a9a38}{\boldsymbol{s}}^2\end{align}|| |
Volume of Cubes||V=\color{#3a9a38}{\boldsymbol{s}}^3|| |
|
Prism 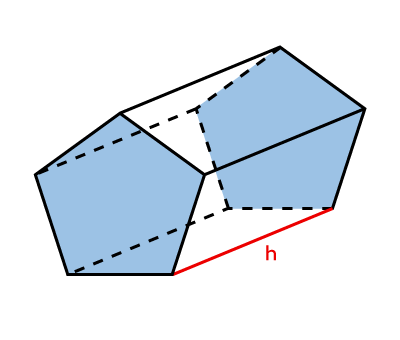 |
Area of Prisms||\begin{align}\color{#3b87cd}{\boldsymbol{A_b}}&=\text{relevant formula}\\\\A_L&=P_b\times\color{#ec0000}{\boldsymbol{h}}\\\\A_T&=A_L+2\color{#3b87cd}{\boldsymbol{A_b}}\end{align}|| |
Volume of Prisms||V=\color{#3b87cd}{\boldsymbol{A_b}}\times\color{#ec0000}{\boldsymbol{h}}|| |
|
Pyramid 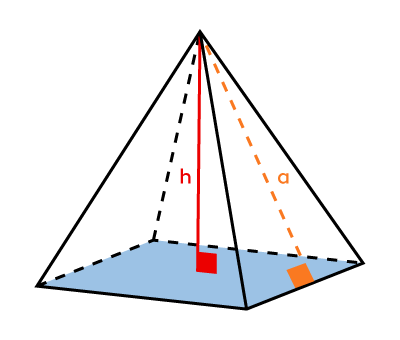 |
Area of Pyramids||\begin{align}\color{#3b87cd}{\boldsymbol{A_b}}&=\text{relevant formula}\\\\A_L&=\dfrac{P_b\times\color{#fa7921}{\boldsymbol{a}}}{2}\\\\A_T&=A_L+\color{#3b87cd}{\boldsymbol{A_b}}\end{align}|| |
Volume of Pyramids||V=\dfrac{\color{#3b87cd}{\boldsymbol{A_b}}\times\color{#ec0000}{\boldsymbol{h}}}{3}|| |
|
Sphere  |
Area of Spheres||A_T=4\pi\color{#3a9a38}{\boldsymbol{r}}^2|| |
Volume of Spheres||V=\dfrac{4\pi\color{#3a9a38}{\boldsymbol{r}}^3}{3}|| |
|
Cylinder 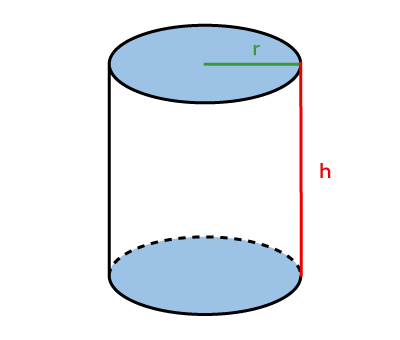 |
Area of Cylinders||\begin{align}\color{#3b87cd}{\boldsymbol{A_b}}&=\pi\color{#3a9a38}{\boldsymbol{r}}^2\\\\A_L&=2\pi\color{#3a9a38}{\boldsymbol{r}}\color{#ec0000}{\boldsymbol{h}}\\\\A_T&=A_L+2\color{#3b87cd}{\boldsymbol{A_b}}\end{align}|| |
Volume of Cylinders||V=\color{#3b87cd}{\boldsymbol{A_b}}\times\color{#ec0000}{\boldsymbol{h}}|| |
|
Cone 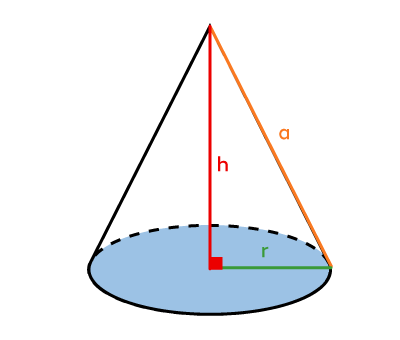 |
Area of Cones||\begin{align}\color{#3b87cd}{\boldsymbol{A_b}}&=\pi\color{#3a9a38}{\boldsymbol{r}}^2\\\\A_L&=\pi\color{#3a9a38}{\boldsymbol{r}}\color{#fa7921}{\boldsymbol{a}}\\\\A_T&=A_L+\color{#3b87cd}{\boldsymbol{A_b}}\end{align}|| |
Volume of Cones||V=\dfrac{\color{#3b87cd}{\boldsymbol{A_b}}\times\color{#ec0000}{\boldsymbol{h}}}{3}|| |