Equivalent Figures have the same area.
Congruent/isometric figures are necessarily equivalent figures.
However, equivalent figures are not necessarily congruent figures. In fact, 2 equivalent figures can be completely different.
We can prove that the following triangle |\color{#333fb1}{ABC}| and square |\color{#fa7921}{IJKL}| are equivalent by calculating their respective areas.
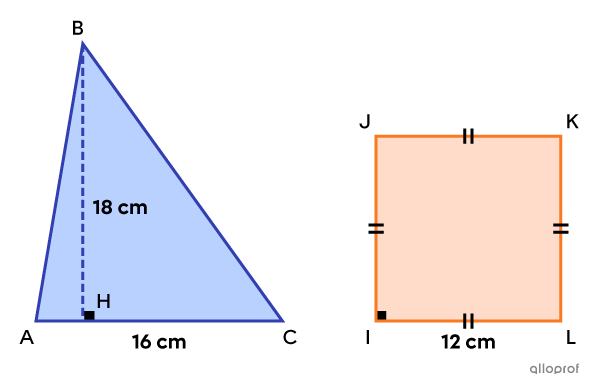
||\begin{align}A_\text{triangle}&=\dfrac{\text{m}\overline{AC}\times\text{m}\overline{BH}}{2}\\&=\dfrac{16\times18}{2}\\&=144\ \text{cm}^2\end{align}||
||\begin{align}A_\text{square}&=\left(\text{m}\overline{IL}\right)^2\\&=12^2\\&=144\ \text{cm}^2\end{align}||
Conclusion: The triangle |\color{#333fb1}{ABC}| and the square |\color{#fa7921}{IJKL}| are equivalent since they each have an area of |144\ \text{cm}^2.|
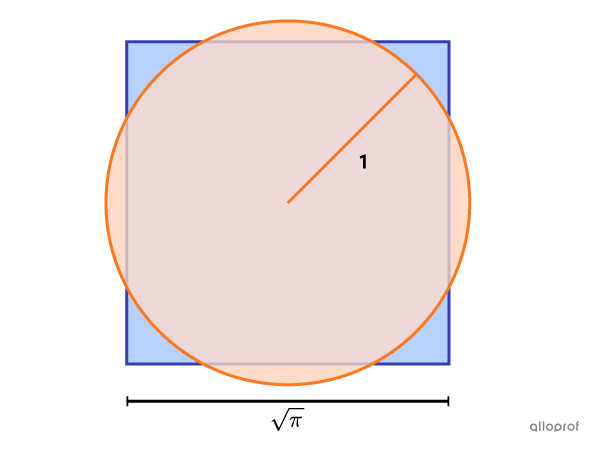
Considered one of the 3 great problems of mathematics in Antiquity, squaring the circle is a problem concerning equivalent figures. The objective of this problem, of which the first written trace can be found on the famous Rhind Papyrus from Egypt, is to demonstrate how to construct a square with a ruler and a compass whose area is equivalent to that of a given circle.
In 1882, after nearly 3 000 years, the German mathematician Ferdinand von Lindemann proved that this construction is impossible to achieve.
Algebra is often needed to find missing measurements in equivalent figures. Here is how to do so.
-
Determine the equation formed by the equivalence between the area of the figures.
-
Solve the equation.
-
Answer the question.
Here is a 1st example where there is only one unknown.
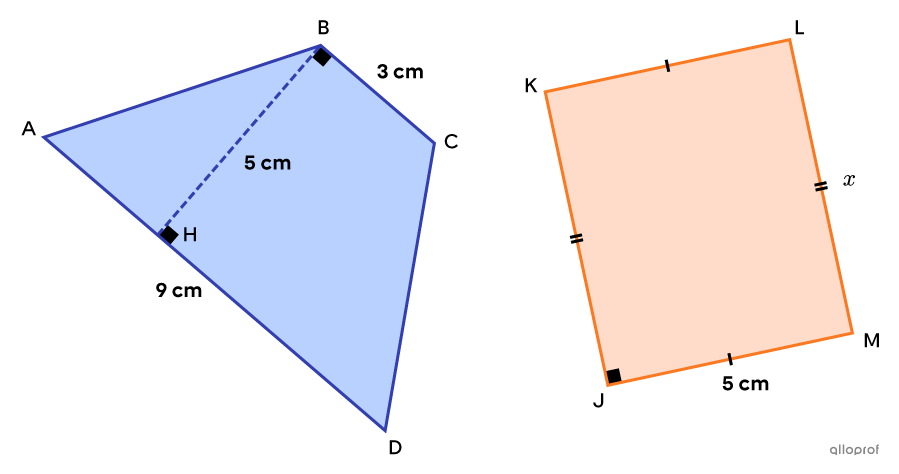
Find the height of rectangle |\color{#fa7921}{JKLM},| knowing that it is equivalent to trapezoid |\color{#333fb1}{ABCD}.|
-
Determine the equation formed by the equivalence between the areas of the figures.
We start by finding the area of the trapezoid and the rectangle from the information provided.
||\begin{align}A_\text{trapezoid}&=\dfrac{\left(\text{m}\overline{AD}+\text{m}\overline{BC}\right)\times\text{m}\overline{BH}}{2}\\&=\dfrac{(9+3)\times5}{2}\\&=30\ \text{cm}^2\end{align}||
||\begin{align}A_\text{rectangle}&=\text{m}\overline{JM}\times\text{m}\overline{LM}\\&=5x\end{align}||
We get the following equation:
||\begin{align}\color{#333fb1}{A_\text{trapezoid}}&=\color{#fa7921}{A_\text{rectangle}}\\\color{#333fb1}{30}&=\color{#fa7921}{5x}\end{align}||
-
Solve the equation.
||\begin{align}\color{#ec0000}{\dfrac{\color{black}{30}}{5}}&=\color{#ec0000}{\dfrac{\color{black}{5x}}{5}}\\6\ \text{cm}&=x\end{align}|| -
Answer the question.
The height of rectangle |\color{#fa7921}{JKLM}| is |6\ \text{cm}.|
Here is a 2nd example where there are many unknowns.
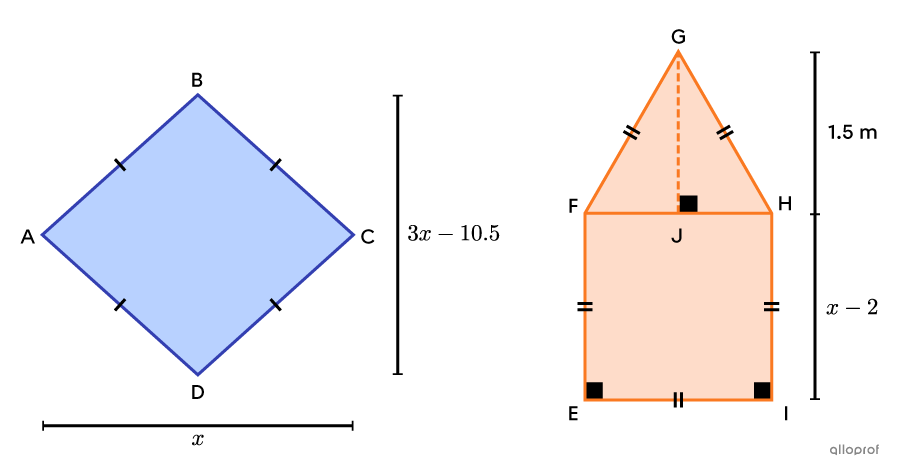
Find the height of the pentagon |\color{#fa7921}{EFGHI},| knowing that it is equivalent to the rhombus |\color{#333fb1}{ABCD}.|
-
Determine the equation formed by the equivalence between the areas of the figures.
We start by finding the area of the rhombus |\color{#333fb1}{ABCD}| and that of the pentagon |\color{#fa7921}{EFGHI}| from the information provided. Notice that the pentagon is a decomposable figure that can be broken down into a square and an equilateral triangle.
||\begin{align}A_\text{rhombus}&=\dfrac{\text{m}\overline{AC}\times\text{m}\overline{BD}}{2}\\&=\dfrac{x(3x-10.5)}{2}\end{align}||
Area of the Decomposable Pentagon
||\begin{align}A_\text{pentagon}&=A_\text{square}+A_\text{triangle}\\&=\left(\text{m}\overline{HI}\right)^2+\dfrac{\text{m}\overline{HF}\times\text{m}\overline{JG}}{2}\\&=(x-2)^2+\dfrac{(x-2)\times1.5}{2}\end{align}||
We get the following equation:
||\begin{align}\color{#333fb1}{A_\text{rhombus}}&=\color{#fa7921}{A_\text{pentagon}}\\\color{#333fb1}{\dfrac{x(3x-10.5)}{2}}&=\color{#fa7921}{(x-2)^2+\dfrac{(x-2)\times1.5}{2}}\end{align}||
-
Solve the equation.
Next, we multiply both sides of the equation by |2| to eliminate the fractions, and we collect the like terms.
||\begin{align}\dfrac{x(3x-10.5)}{2}\color{#ec0000}{\times2}&=\color{#ec0000}{\left(\color{black}{(x-2)^2+\dfrac{1.5(x-2)}{2}}\right)\times2}\\x(3x-10.5)&=2(x-2)^2+1.5(x-2)\\3x^2-10.5x&=2(x^2-4x+4)+1.5x-3\\3x^2-10.5x&=2x^2-8x+8+1.5x-3\\x^2-4x-5&=0\end{align}||
To solve this 2nd degree (quadratic) equation, we can use the quadratic formula.
||\begin{align}x&=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}\\&=\dfrac{-(-4)\pm\sqrt{(-4)^2-4(1)(-5)}}{2(1)}\\&=\dfrac{4\pm\sqrt{36}}{2}\\\\x_1&=-1\ \text{m}\quad\text{and}\quad x_2=5\ \text{m}\end{align}||
We must reject the solution |x_1=-1\ \text{m}| since it would imply that the measure of the diagonal |\overline{AC}| of rhombus |\color{#333fb1}{ABCD}| is negative. The solution sought is therefore |x_2=5\ \text{m}.|
-
Answer the question.
||\begin{align}h_\text{pentagon}&=\text{m}\overline{JG}+\text{m}\overline{HI}\\&=1.5+\color{#333fb1}{x}-2\\&=1.5+\color{#333fb1}{5}-2\\&=4.5\ \text{m}\end{align}||
Therefore, the height of the pentagon |\color{#fa7921}{EFGHI}| is |4.5\ \text{m}.|
Some conjectures can be made about the perimeters of equivalent plane figures. We examine several examples to verify that each of these propositions is true.
Amongst all of the equivalent polygons with |n| sides, the regular polygon has the smallest perimeter.
This conjecture is similar to that concerning the smallest area amongst equivalent prisms.
Consider the following rectangle |\color{#333fb1}{ABCD},| kite |\color{#fa7921}{IJKL}| and square |\color{#7cca51}{EFGH}.|

These 3 quadrilaterals are equivalent, since they each have an area of |64\ \text{dm}^2.|
||\begin{align}A_\text{rectangle}&=\text{m}\overline{AB}\times\text{m}\overline{BC}\\&=16\times 4\\&=64\ \text{dm}^2\end{align}||
||\begin{align}A_\text{kite} &=\dfrac{\text{m}\overline{IK}\times\text{m}\overline{JL}}{2}\\A_\text{kite}&=\dfrac{(4+4)\times(10+6)}{2}\\A_\text{kite}&=64\ \text{dm}^2\end{align}||
||\begin{align}A_\text{square} &=\left(\text{m}\overline{EF}\right)^2\\&=8^2\\&=64\ \text{dm}^2\end{align}||
However, each has a different perimeter.
||\begin{align}P_\text{rectangle}&=2\times\text{m}\overline{AB}+2\times\text{m}\overline{BC}\\&=2\times16+2\times4\\&=40\ \text{dm}\end{align}||
||\begin{align}P_\text{kite}&=2\times\text{m}\overline{IJ}+2\times\text{m}\overline{KL}\\&=2\times10.77+2\times7.21\\&=35.96\ \text{dm}\end{align}||
||\begin{align}P_\text{square}&=4\times\text{m}\overline{EF}\\&=4\times8\\&=32\ \text{dm}\end{align}||
Therefore, amongst these 3 equivalent quadrilaterals, the square has the smallest perimeter since it is a regular 4-sided polygon.
Amongst all regular equivalent polygons, the regular polygon with the most sides has the smallest perimeter.
Consider the following regular pentagon, regular hexagon, and regular heptagon.
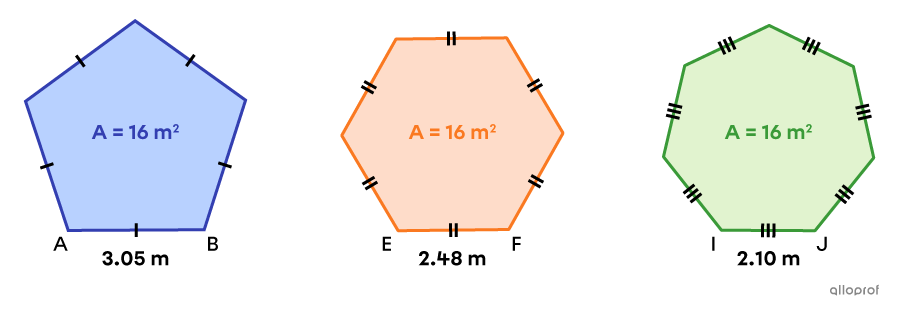
Perimeter of the Regular Pentagon
||\begin{align}P_\text{pentagon}&=n\times\text{m}\overline{AB}\\&=5\times3.05\\&=15.25\ \text{m}\end{align}||
Perimeter of the Regular Hexagon
||\begin{align}P_\text{hexagon}&=n\times\text{m}\overline{EF}\\&=6\times2.48\\&=14.88\ \text{m}\end{align}||
Perimeter of the Regular Heptagon
||\begin{align}P_\text{heptagon}&=n\times\text{m}\overline{EF}\\&=7\times2.10\\&=14.70\ \text{m}\end{align}||
Amongst these 3 equivalent regular polygons, the regular heptagon has the smallest perimeter, since it’s the one with the largest number of sides.
Amongst all equivalent plane figures, the circle has the smallest perimeter.
This conjecture is similar to that concerning the smallest area amongst equivalent solids.
Consider the following parallelogram |\color{#333fb1}{ABCD},| triangle |\color{#fa7921}{EFG},| and circle with radius |\color{#7cca51}{OI}.|
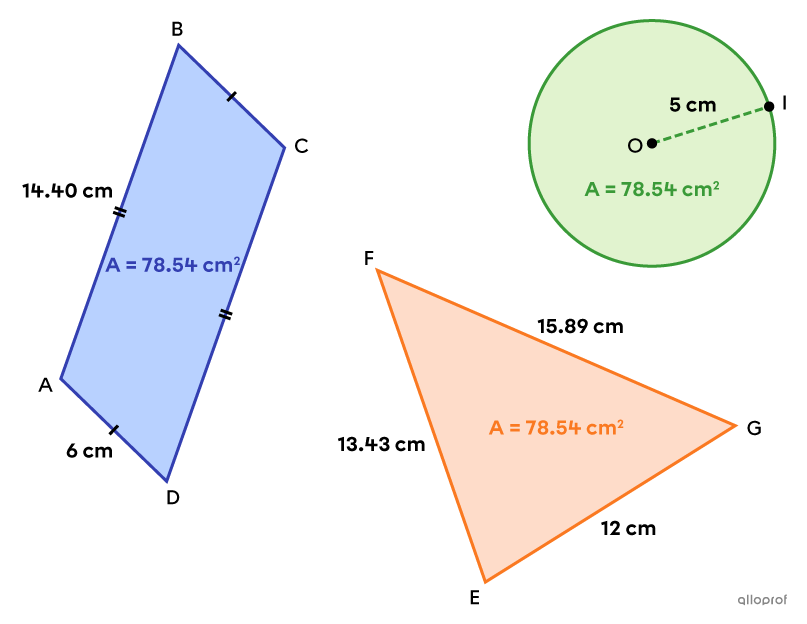
These 3 figures are equivalent since they each have an area of |78.54\ \text{cm}^2.| However, each has a different perimeter.
||\begin{align}P_\text{triangle}&=\text{m}\overline{EF}+\text{m}\overline{FG}+\text{m}\overline{GE}\\&=13.43+15.89+12\\&=41.32\ \text{cm}\end{align}||
Perimeter of the Parallelogram
||\begin{align}P_\text{parallelogram}&=2\times\text{m}\overline{DA}+2\times\text{m}\overline{AB}\\&=2\times6+2\times14.40\\&=40.80\ \text{cm}\end{align}||
||\begin{align}C_\text{circle}&=2\pi\times\text{m}\overline{OI}\\&=2\pi\times5\\&\approx31.42\ \text{cm}\end{align}||
Therefore, amongst these 3 equivalent plane figures, the circle has the smallest perimeter.
The following animation summarizes the 3 preceding conjectures.
By moving the cursor Number of Sides |(n),| we see that as the number of sides increases, the more the perimeter |(P)| decreases towards a certain value. This value corresponds to the circumference of the circle that is equivalent to all these regular polygons.
We can prove an algebraic relationship that gives the perimeter of a regular polygon as a function of its area.
|P=2\sqrt{A\times n\times\tan\dfrac{180^\circ}{n}}|
where
|P:| perimeter of the regular polygon
|A:| area of the regular polygon
|n:| number of sides of the regular polygon
As can be seen in the previous interactive animation, all regular polygons with |n| sides are decomposable into |n| isometric triangles. We will take the regular pentagon as an example to first define each of the variables.
|s:| side
|a:| apothem
|\theta:| central angle
The perimeter |(P)| and area |(A)| of a regular polygon are given by the following expressions:
||\begin{align}P&=n\times s\\\\A&=\dfrac{s\times a\times n}{2}\end{align}||
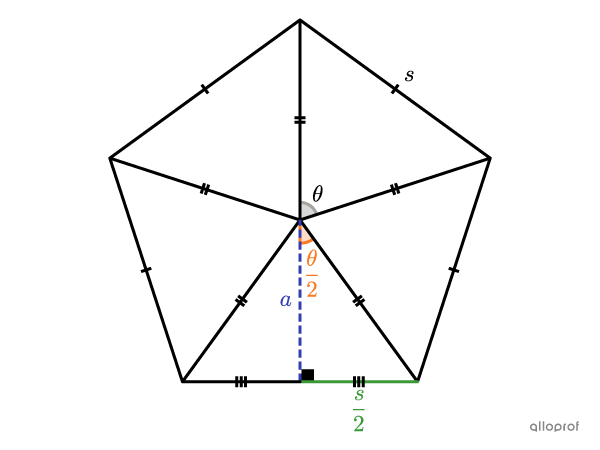
We isolate |s| in the area equation to substitute it in the perimeter equation.
||\begin{align}A&=\dfrac{s\times a\times n}{2}\\2A&=s\times a\times n\\\dfrac{2A}{a\times n}&=s\\\\P&=n\times\color{#7cca51}{s}\\P&=n\times\color{#7cca51}{\dfrac{2A}{a\times n}}\\P&=\dfrac{2A}{a}\end{align}||
This equation gives the perimeter of a regular polygon as a function of its area |(A)| and its apothem |(a).| Using the tangent ratio in the right triangle, which is half of the isosceles triangle, we can establish a relationship between the apothem, half of the side, and half of the central angle of the polygon.
||\begin{align}\tan\color{#fa7921}{\dfrac{\theta}{2}}&=\dfrac{\color{#7cca51}{\dfrac{s}{2}}}{\color{#333fb1}{a}}\\a\times\tan\dfrac{\theta}{2}&=\dfrac{s}{2}\\a&=\dfrac{s}{2\tan\frac{\theta}{2}}\end{align}||
We substitute |s| with the same expression as before, then we isolate |a.|
||\begin{align}a&=\dfrac{\color{#7cca51}{s}}{2\tan\frac{\theta}{2}}\\a&=\dfrac{\color{#7cca51}{\dfrac{2A}{a\times n}}}{2\tan\frac{\theta}{2}}\\a&=\dfrac{2A}{a\times n}\times\dfrac{1}{2\tan\frac{\theta}{2}}\\a&=\dfrac{A}{a\times n\times\tan\frac{\theta}{2}}\\a^2&=\dfrac{A}{n\times\tan\frac{\theta}{2}}\\a&=\sqrt{\dfrac{A}{n\times\tan\frac{\theta}{2}}}\end{align}||
We substitute |a| in the perimeter equation with the expression we just found, and simplify.
||\begin{align}P&=\dfrac{2A}{\color{#333fb1}{a}}\\ P&=\dfrac{2A}{\color{#333fb1}{\sqrt{\dfrac{A}{n\times\tan\frac{\theta}{2}}}}}\\ P&=2A\times\sqrt{\dfrac{n\times\tan\frac{\theta}{2}}{A}}\\P&=2\sqrt{A^2\times\dfrac{n\times\tan\frac{\theta}{2}}{A}}\\P&=2\sqrt{A\times n\times\tan\frac{\theta}{2}}\end{align}||
Finally, we substitute |\theta| with the expression for the central angle of a regular polygon.
||\begin{align}P&=2\sqrt{A\times n\times\tan\frac{\color{#fa7921}{\theta}}{2}}\\P&=2\sqrt{A\times n\times\tan\dfrac{\color{#fa7921}{\frac{360^{\circ}}{n}}}{2}}\\P&=2\sqrt{A\times n\times\tan\dfrac{180^{\circ}}{n}}\end{align}||