The study of vectors draws on many of the geometric and trigonometric concepts covered in earlier years.
To calculate a vector's components, you need to know how to apply trigonometric ratios in a right triangle. To calculate the norm of a vector, you can use the Pythagorean Theorem or the distance between 2 points formula. Finally, to add or subtract vectors, you may need to use the Law of Sines and the Law of Cosines. It's a good idea to brush up on these concepts before watching these Crash Course videos.
Before performing operations on vectors, you need to know the related vocabulary:
-
A scalar is a quantity that is defined by a real number, whereas a vector is defined by both a number AND a direction.
-
The magnitude (or norm) of a vector |\overrightarrow{v},| denoted |{\parallel}\overrightarrow{v}{\parallel}|, is its length.
-
The direction of a vector |(\theta_{\overrightarrow{v}})| refers to its orientation (indicated by the arrowhead on the vector). The direction is an angle measured counterclockwise from the positive |x| axis.
-
The components |(a,b)| of a vector represent its horizontal displacement |(a)| and vertical displacement |(b)| required to move from the vector's origin to its endpoint.
-
Two vectors are equipollent if they have the same magnitude and orientation.
-
Two vectors are opposite if they have the same magnitude, are parallel but have opposite directions.
-
Two vectors are collinear if they are parallel.
-
Two vectors are orthogonal if they are perpendicular.
From the magnitude of a vector |({\parallel}\overrightarrow{v}{\parallel})| and its direction, |(\theta_{\overrightarrow{v}}),| we can calculate its components |(a,b)|: ||a = {\parallel}\overrightarrow{v}{\parallel} \cos \theta_{\overrightarrow{v}}|| ||b={\parallel}\overrightarrow{v}{\parallel} \sin \theta_{\overrightarrow{v}}||
Draw a right triangle using the components of the vector, and calculate its magnitude using the Pythagorean Theorem, and calculate its orientation using the tangent ratio.
To perform the various operations on vectors (addition, subtraction, scalar product, etc.), it's best to work with their components:
Adding vectors: Add the horizontal components together, then do the same for the vertical components.
Example: ||(3,-5) + (6,2) = (3+6, -5+2) = (9, -3)||
Subtracting vectors: Subtract the horizontal components from each other, and do the same for the vertical components.
Example: ||(3,-5) - (6,2) = (3-6, -5-2) = (-3, -7)||
Multiplying a vector by a scalar: Distribute the scalar to each of the vector components.
Example: ||5(2,-6) = (5\times 2, 5\times -6) = (10,-30)||
Scalar product (dot product): Add the product of the horizontal components to the product of the vertical components.
Example: ||\begin{align} (-2,3)\cdot (5,4) &= -2\times 5 + 3 \times 4 \\ &= -10+12 \\ &=2 \end{align}||
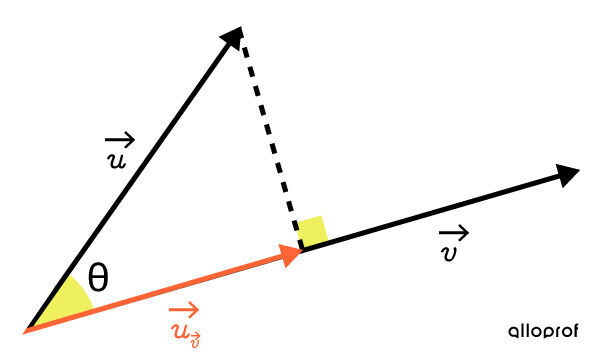
Orthogonal Projection
In the following figure, the orthogonal projection of |\overrightarrow{u}| onto |\overrightarrow{v}| is the vector |\overrightarrow{u}_{\overrightarrow{v}}.|
To calculate the magnitude of this orthogonal projection, the following formula can be used: ||{\parallel}\overrightarrow{u}_\overrightarrow{v}{\parallel} = {\parallel}\overrightarrow{u}{\parallel} \cos \theta||where |\theta=| the acute angle between |\overrightarrow{u}| and |\overrightarrow{v}|
To calculate the components of this orthogonal projection, use the following formula instead: ||\overrightarrow{u}_{\overrightarrow{v}}=\dfrac{\overrightarrow{u} \cdot \overrightarrow{v}}{\parallel \overrightarrow{v} \parallel^2} \overrightarrow{v}||
Linear Combinations (Secondary 5 SN math only)
Two non-parallel vectors can be combined to create any vector in the Cartesian plane. The linear combination can be represented by the following equation: ||\overrightarrow{v}=a\overrightarrow{u_1}+b\overrightarrow{u_2}||where |a| and |b| are scalars and |\overrightarrow{u_1}| and |\overrightarrow{u_2}| are non-parallel vectors that form a vector basis.
To find the value of the coefficients |a| and |b,| a system of equations made from the |x| and |y| components has to be solved.