Solids with the same area are solids that have identical total areas.
Congruent (isometric) solids are always equivalent solids and have the same total area.
However, equivalent solids or solids with the same area are not necessarily isometric solids. In fact, 2 solids with the same area can be completely different.
We can prove that the following pyramid and square-based prism have the same area by calculating their respective total areas.
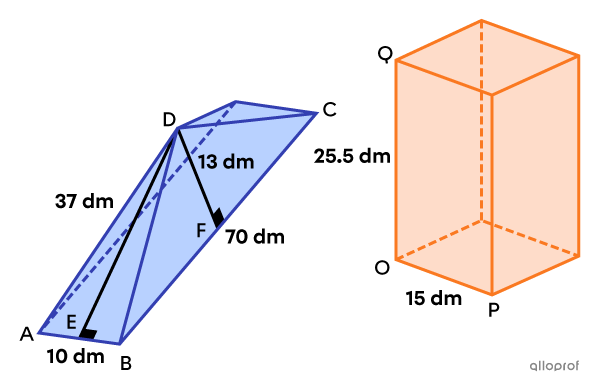
||\begin{align}A_\text{base}&=\text{m}\overline{AB}\times\text{m}\overline{BC}\\&=10\times70\\&=700\ \text{dm}^2\\\\A_\text{lateral}&=2\left(\dfrac{\text{m}\overline{AB}\times\text{m}\overline{DE}}{2}+\dfrac{\text{m}\overline{BC}\times\text{m}\overline{DF}}{2}\right)\\&=\text{m}\overline{AB}\times\text{m}\overline{DE}+\text{m}\overline{BC}\times\text{m}\overline{DF}
\\&=10\times37+70\times13\\&=1\ 280\ \text{dm}^2\\\\A_\text{pyramid}&=A_\text{base}+A_\text{lateral}\\&=700+1\ 280\\&=1\ 980\ \text{dm}^2\end{align}||
||\begin{align}A_\text{prism}&=2A_\text{base}+A_\text{lateral}\\&=2\left(\text{m}\overline{OP}\right)^2+4\times\text{m}\overline{OP}\times\text{m}\overline{OQ}\\&=2\times15^2+4\times15\times25.5\\&=1\ 980\ \text{dm}^2\end{align}||
Conclusion: The pyramid and the prism both have a total area of |1\ 980\ \text{dm}^2.|
It is often necessary to use algebra to find missing measurements in solids with the same area. Here is how to do so.
-
Determine the equation formed by the equivalence between the total area of the solids.
-
Solve the equation.
-
Answer the question.
Here is a 1st example where there is only one unknown.
Find the radius of the sphere, given that it has the same area as the cylinder.
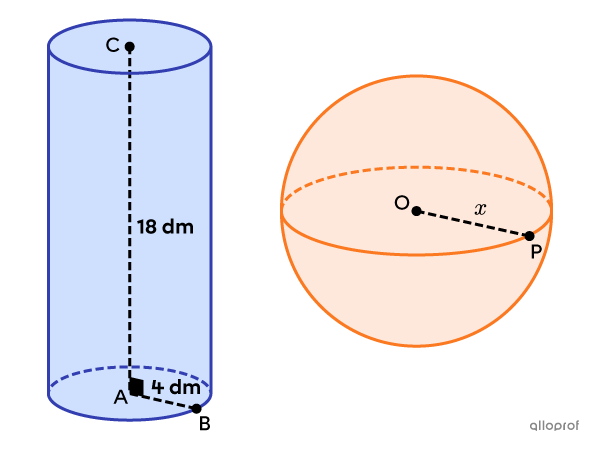
-
Determine the equation formed by the equivalence between the total area of the solids.
We start by finding the total area of both the cylinder and the sphere from the information provided.
||\begin{align}A_\text{cylinder}&=2A_\text{base}+A_\text{lateral}\\&=2\pi\left(\text{m}\overline{AB}\right)^2+2\pi\times\text{m}\overline{AB}\times\text{m}\overline{AC}\\&=2\pi\times4^2+2\pi\times4\times18\\&=176\pi\ \text{dm}^2\end{align}||
||\begin{align}A_\text{sphere}&=4\pi\left(\text{m}\overline{OP}\right)^2\\&=4\pi x^2\end{align}||
We get the following equation:
||\begin{align}\color{#333fb1}{A_\text{cylinder}}&=\color{#fa7921}{A_\text{sphere}}\\\color{#333fb1}{176\pi}&=\color{#fa7921}{4\pi x^2}\end{align}||
-
Solve the equation.
||\begin{align}\color{#ec0000}{\dfrac{\color{black}{176\pi}}{4\pi}}&=\color{#ec0000}{\dfrac{\color{black}{4\pi x^2}}{4\pi}}\\\color{#ec0000}{\sqrt{\color{black}{44}}}&=\color{#ec0000}{\sqrt{\color{black}{x^2}}}\\\pm\,6.63\ \text{dm}&\approx x\end{align}||
We must reject the solution |x\approx-6.63\ \text{dm},| since the measure of the radius |\overline{OP}| can’t be negative.
-
Answer the question.
The radius of the sphere is approximately |6.63\ \text{dm}.|
Here is a 2nd example where there are many unknowns.
Find the apothem of the pyramid, given that it has the same area as the cone.
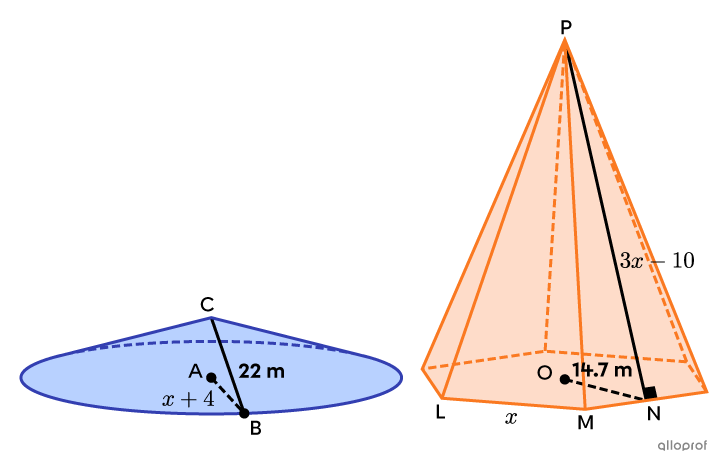
-
Determine the equation formed by the equivalence between the total area of the solids.
We start by finding the total area of the cone and the pyramid from the information provided.
||\begin{align}A_\text{base}&=\pi\left(\text{m}\overline{AB}\right)^2\\&=\pi(x+4)^2\\\\A_\text{lateral}&=\pi\times\text{m}\overline{AB}\times\text{m}\overline{BC}\\&=\pi(x+4)(22)\\&=22\pi(x+4)\\\\A_\text{cone}&=A_\text{base}+A_\text{lateral}\\&=\pi(x+4)^2+22\pi(x+4)\end{align}||
||\begin{align}A_\text{base}&=\dfrac{6\times\text{m}\overline{LM}\times\text{m}\overline{NO}}{2}\\&=3\times x\times14.7\\&=44.1x\\\\A_\text{lateral}&=6\times\dfrac{\text{m}\overline{LM}\times\text{m}\overline{NP}}{2}\\&=3\times x\times(3x-10)\\&=9x^2-30x\\\\A_\text{pyramid}&=A_\text{base}+A_\text{lateral}\\&=44.1x+9x^2-30x\\&=9x^2+14.1x\end{align}||
We get the following equation:
||\begin{align}\color{#333fb1}{A_\text{cone}}&=\color{#fa7921}{A_\text{pyramid}}\\\color{#333fb1}{\pi(x+4)^2+22\pi(x+4)}&=\color{#fa7921}{9x^2+14.1x}\end{align}||
-
Solve the equation.
First we expand the left-hand side, then we group the like terms on the same side of the equation.
||\begin{align}\pi(x+4)^2+22\pi(x+4)&=9x^2+14.1x\\\pi(x^2+8x+16)+22\pi x+88\pi&=9x^2+14.1x\\\pi x^2+8\pi x+16\pi+22\pi x+88\pi&=9x^2+14.1x\\\pi x^2+30\pi x+104\pi&=9x^2+14.1x\\-5.86x^2+80.15x+326.73&\approx0\end{align}||
To solve this 2nd degree (quadratic) equation, we can use the quadratic formula.
||\begin{align}x&=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}\\&=\dfrac{-(80.15)\pm\sqrt{(80.15)^2-4(-5.86)(326.73)}}{2(-5.86)}\\&\approx\dfrac{-80.15\pm\sqrt{14\ 082.57}}{-11.72}\\\\x_1&\approx16.96\ \text{m}\quad\text{and}\quad x_2\approx-3.29\ \text{m}\end{align}||
We must reject the solution |x_2\approx-3.9\ \text{m},| since it would imply that the measure of the pyramid’s edge |\overline{LM}| is negative. The solution is therefore |x_1\approx16.96\ \text{m}.| -
Answer the question.
||\begin{align}a_\text{pyramid}&=\text{m}\overline{NP}\\&=3\color{#fa7921}{x}-10\\&=3(\color{#fa7921}{16.96})-10\\&=40.88\ \text{m}\end{align}||
Therefore, the apothem of the pyramid is approximately |40.88\ \text{m}.|
Appearances are sometimes deceiving! In the previous example, we may think that the cone and the pyramid do not have the same total area, since the volume of the pyramid is definitely larger than that of the cone. However, the area of these 2 solids is indeed equal.
Some conjectures can be drawn about the volume of solids with the same area. We examine several examples to verify that each of these propositions is true.
Amongst all rectangular prisms with the same area, the cube has the largest volume.
This conjecture is the inverse of that which concerns the smallest area amongst equivalent prisms.
Consider the following cube and rectangular-based right prisms.
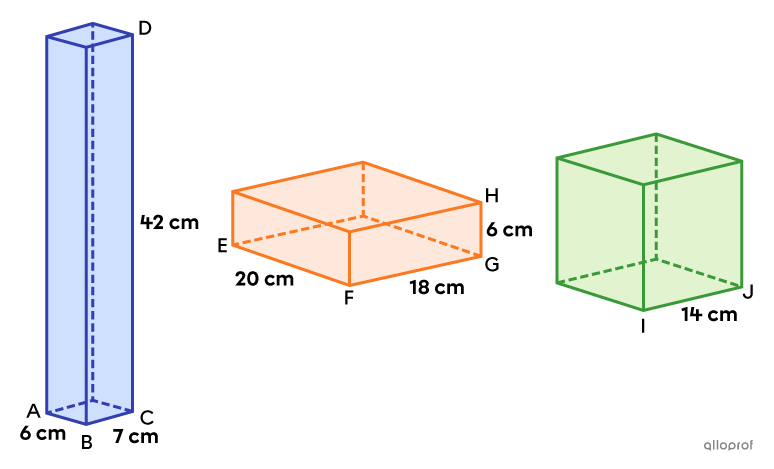
These 3 prisms each have a total area of |1\ 176\ \text{cm}^2.|
Total Area of the Blue Prism
||\begin{align}A_\text{base}&=\text{m}\overline{AB}\times\text{m}\overline{BC}\\&=6\times7\\&=42\ \text{cm}^2\\\\A_\text{lateral}&=\left(2\times\text{m}\overline{AB}+2\times \text{m}\overline{BC}\right)\times\text{m}\overline{CD}\\&=(2\times6+2\times7)\times42\\&=1\ 092\ \text{cm}^2\\\\A_\text{blue prism}&=2A_\text{base}+A_\text{lateral}\\&=2\times42+1\ 092\\&=1\ 176\ \text{cm}^2\end{align}||
Total Area of the Orange Prism
||\begin{align}A_\text{base}&=\text{m}\overline{EF}\times\text{m}\overline{FG}\\&=20\times18\\&=360\ \text{cm}^2\\\\A_\text{lateral}&=\left(2\times\text{m}\overline{EF}+2\times\text{m}\overline{FG}\right)\times\text{m}\overline{GH}\\&=(2\times20+2\times18)\times6\\&=456\ \text{cm}^2\\\\A_\text{orange prism}&=2A_\text{base}+A_\text{lateral}\\&=2\times360+456\\&=1\ 176\ \text{cm}^2\end{align}||
||\begin{align}A_\text{cube}&=6\left(\text{m}\overline{IJ}\right)^2\\&=6\times14^2\\&=1\ 176\ \text{cm}^2\end{align}||
However, each volume is different.
Volume of the Blue Prism
||\begin{align}V_\text{blue prism}&=\text{m}\overline{AB}\times\text{m}\overline{BC}\times\text{m}\overline{CD}\\&=6\times7\times42\\&=1\ 764\ \text{cm}^3\end{align}||
Volume of the Orange Prism
||\begin{align}V_\text{orange prism}&=\text{m}\overline{EF}\times\text{m}\overline{FG}\times\text{m}\overline{GH}\\&=20\times18\times6\\&=2\ 160\ \text{cm}^3\end{align}||
||\begin{align}V_\text{cube}&=\left(\text{m}\overline{IJ}\right)^3\\&=14^3\\&=2\ 744\ \text{cm}^3\end{align}||
Therefore, among these 3 rectangular-based prisms with the same area, the cube has the largest volume.
Amongst all solids with the same area, the sphere has the largest volume.
This conjecture is the inverse of that which concerns the smallest area amongst equivalent solids.
Consider the following cube, regular octahedron and sphere.
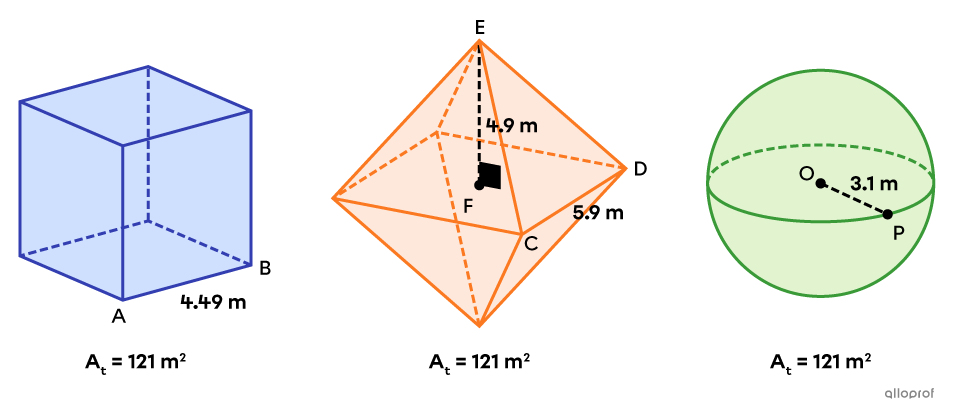
These three solids all have a total area of |121\ \text{m}^2.| However, each of their volumes is different.
||\begin{align}V_\text{cube}&=\left(\text{m}\overline{AB}\right)^3\\&=4.49^3\\&\approx90.52\ \text{m}^3\end{align}||
Volume of the Octahedron
A regular octahedron is a decomposable solid made of 2 square-based pyramids. We can calculate its volume as follows:
||\begin{align}V_\text{octahedron}&=2\times V_\text{pyramid}\\&=2\times\dfrac{\left(\text{m}\overline{CD}\right)^2\times\text{m}\overline{EF}}{3}\\&=2\times\dfrac{5.9^2\times4.19}{3}\\&\approx97.24\ \text{m}^3\end{align}||
||\begin{align}V_\text{sphere}&=\dfrac{4\pi\left(\text{m}\overline{OP}\right)^3}{3}\\&=\dfrac{4\pi\times3.1^3}{3}\\&\approx124.79\ \text{m}^3\end{align}||
Therefore, amongst these 3 solids with the same area, the sphere has the largest volume.