Equivalent solids are solids that have the same volume.
Congruent solids are necessarily equivalent solids and have the same total area.
However, equivalent solids or solids with the same area are not necessarily congruent solids. In fact, 2 equivalent solids can be completely different.
We can prove that the following pyramid and the cube are equivalent by calculating their respective volumes.
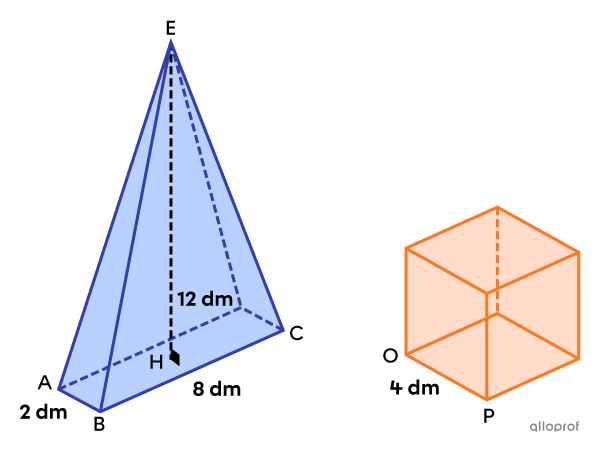
||\begin{align}V_\text{pyramid}&=\dfrac{\text{m}\overline{AB}\times\text{m}\overline{BC}\times\text{m}\overline{EH}}{3}\\&=\dfrac{2\times8\times12}{3}\\&=64\ \text{dm}^3\end{align}||
||\begin{align}V_\text{cube}&=\left(\text{m}\overline{OP}\right)^3\\&=4^3\\&=64\ \text{dm}^3\end{align}||
Conclusion: The pyramid and the cube are equivalent since they each have a volume of |64\ \text{dm}^3.|
It is often necessary to use algebra to find missing measurements in equivalent solids. Here is how to proceed to do so.
-
Determine the equation made from the equivalence between the volume of the solids.
-
Solve the equation
-
Answer the question
Here is a 1st example where there is only one unknown.
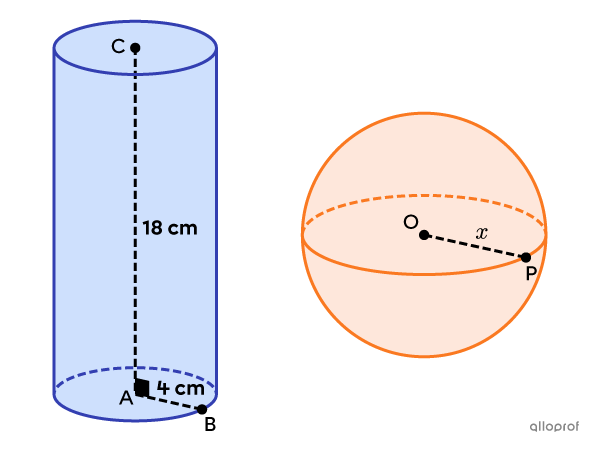
Find the radius of the sphere, given that it is equivalent to the cylinder.
-
Determine the equation made from the equivalence between the volume of the solids.
We start by finding the volume of the cylinder and the sphere from the information provided.
||\begin{align}V_\text{cylinder}&=\pi\times\left(\text{m}\overline{AB}\right)^2\times\text{m}\overline{AC}\\&=\pi\times4^2\times18\\&=288\pi\ \text{cm}^3\end{align}||
||\begin{align}V_\text{sphere}&=\dfrac{4\pi\left(\text{m}\overline{OP}\right)^3}{3}\\&=\dfrac{4\pi x^3}{3}\end{align}||
We get the following equation:
||\begin{align}\color{#333fb1}{V_\text{cylinder}}&=\color{#fa7921}{V_\text{sphere}}\\\color{#333fb1}{288\pi}&=\color{#fa7921}{\dfrac{4\pi x^3}{3}}\end{align}||
-
Solve the equation
||\begin{align}288\pi\color{#ec0000}{\times3}&=\dfrac{4\pi x^3}{3}\color{#ec0000}{\times3}\\\color{#ec0000}{\dfrac{\color{black}{864\pi}}{4\pi}}&=\color{#ec0000}{\dfrac{\color{black}{4\pi x^3}}{4\pi}}\\\color{#ec0000}{\sqrt[3]{\color{black}{216}}}&=\color{#ec0000}{\sqrt[3]{\color{black}{x^3}}}\\6\ \text{cm}&=x\end{align}|| -
Answer the question
The radius of the sphere is |6\ \text{cm}.|
Here is a 2nd example where there are many unknowns.
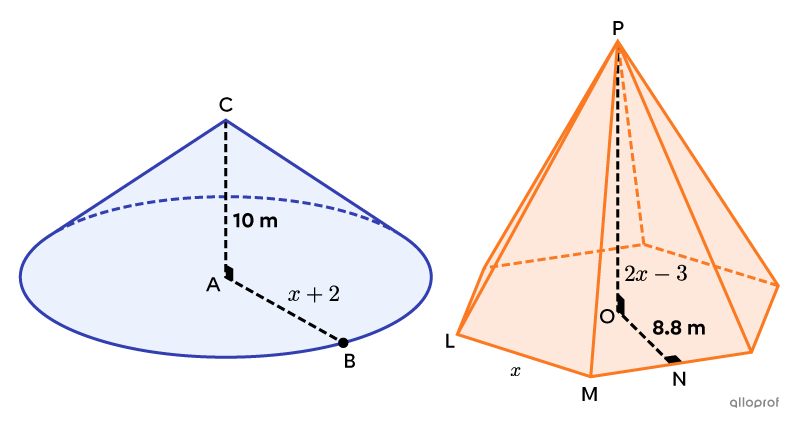
Find the height of the pyramid, given that it is equivalent to the cone.
-
Determine the equation made from the equivalence between the volume of the solids.
We start by finding the volume of the cone and the pyramid from the information provided.
||\begin{align}V_\text{cone}&=\dfrac{\pi\left(\text{m}\overline{AB}\right)^2\times\text{m}\overline{AC}}{3}\\&=\dfrac{\pi(x+2)^2\times10}{3}\end{align}||
||\begin{align}V_\text{pyramid}&=\dfrac{\left(\dfrac{\text{m}\overline{LM}\times\text{m}\overline{NO} \times n}{2}\right)\times\text{m}\overline{OP}}{3}\\&=\dfrac{\left(\dfrac{x\times8.8\times6}{2}\right)\times(2x-3)}{3}\\&=8.8x(2x-3)\end{align}||
We get the following equation:
||\begin{align}\color{#333fb1}{V_\text{cone}}&=\color{#fa7921}{V_\text{pyramid}}\\\color{#333fb1}{\dfrac{10\pi(x+2)^2}{3}}&=\color{#fa7921}{8.8x(2x-3)}\end{align}||
-
Solve the equation
First, we multiply both sides of the equation by |3| to eliminate the fraction. Then, we expand the algebraic expressions, and group the like terms on the same side of the equals sign.
||\begin{align}\color{#ec0000}{\left(\color{black}{\dfrac{10\pi(x+2)^2}{3}}\right)\times3}&=8.8x(2x-3)\color{#ec0000}{\times3}\\10\pi(x+2)^2&=26.4x(2x-3)\\10\pi(x^2+4x+4)&=26.4x(2x-3)\\10\pi x^2+40\pi x+40\pi&=52.8x^2-79.2x\\0&\approx21.38x^2-204.86x-125.66\end{align}||
To solve a second-degree (quadratic) equation, we can use the quadratic equation.
||\begin{align}x&=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}\\&\approx\dfrac{-(-204.86)\pm\sqrt{(-204.86)^2-4(21.38)(-125.66)}}{2(21.38)}\\&\approx\dfrac{204.86\pm\sqrt{52\ 714.06}}{42.76}\\\\x_1&\approx-0.58\ \text{m}\quad\text{and}\quad x_2\approx10.16\ \text{m}\end{align}||
We reject the solution |x_1\approx-0.58\ \text{m},| since it would imply that the measure of the edge |\overline{LM}| of the pyramid is negative. So, the solution is |x_2\approx10.16\ \text{m}.| -
Answer the question
||\begin{align}h_\text{pyramid}&=\text{m}\overline{OP}\\&=2\color{#fa7921}{x}-3\\&\approx2(\color{#fa7921}{10.16})-3\\&\approx17.32\ \text{m}\end{align}||
Therefore, the height of the pyramid is approximately |17.32\ \text{m}.|
Some conjectures can be made about the total area of equivalent solids. We will examine several examples to verify that each of these propositions is true.
Of all equivalent rectangular prisms, the cube has the smallest total area.
This conjecture is similar to the one regarding the smallest perimeter amongst equivalent figures with |n| sides, but it applies specifically to 6-sided right prisms.
Furthermore, this conjecture is the inverse of that regarding the largest volume among prisms of the same area.
Consider the following rectangular-based prisms and cube.
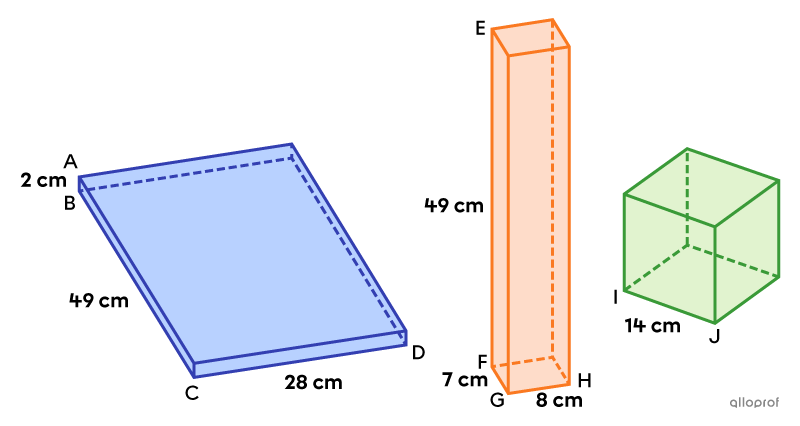
These 3 prisms are equivalent, since they all have a volume of |2\ 744\ \text{cm}^3.|
Volume of the blue prism
||\begin{align}V_\text{blue prism}&=\text{m}\overline{BC}\times\text{m}\overline{CD}\times\text{m}\overline{AB}\\&=49\times28\times2\\&=2\ 744\ \text{cm}^3\end{align}||
Volume of the orange prism
||\begin{align}V_\text{orange prism}&=\text{m}\overline{FG}\times\text{m}\overline{GH}\times\text{m}\overline{EF}\\&=7\times8\times49\\&=2\ 744\ \text{cm}^3\end{align}||
||\begin{align}V_\text{cube}&=\left(\text{m}\overline{IJ}\right)^3\\&=14^3\\&=2\ 744\ \text{cm}^3\end{align}||
However, each total area is different.
Total area of the blue prism
||\begin{align}A_\text{base}&=\text{m}\overline{BC}\times\text{m}\overline{CD}\\&=49\times28\\&=1\ 372\ \text{cm}^2\\\\A_\text{lateral}&=\left(2\times\text{m}\overline{BC}+2\times\text{m}\overline{CD}\right)\times\text{m}\overline{AB}\\&=(2\times49+2\times28)\times2\\&=308\ \text{cm}^2\\\\A_\text{blue prism}&=2A_\text{base}+A_\text{lateral}\\&=2\times1\ 372+308\\&=3\ 052\ \text{cm}^2\end{align}||
Total area of the orange prism
||\begin{align}A_\text{base}&=\text{m}\overline{FG}\times\text{m}\overline{GH}\\&=7\times8\\&=56\ \text{cm}^2\\\\A_\text{lateral}&=\left(2\times\text{m}\overline{FG}+2\times\text{m}\overline{GH}\right)\times\text{m}\overline{EF}\\&=(2\times7+2\times8)\times49\\&=1\ 470\ \text{cm}^2\\\\A_\text{orange prism}&=2A_\text{base}+A_\text{lateral}\\&=2\times56+1\ 470\\&=1\ 582\ \text{cm}^2\end{align}||
||\begin{align}A_\text{cube}&=6\left(\text{m}\overline{IJ}\right)^2\\&=6\times14^2\\&=1\ 176\ \text{cm}^2\end{align}||
Therefore, amongst these 3 equivalent rectangular prisms, the cube has the smallest total area.
Of all equivalent solids, the sphere has the smallest total area.
This conjecture is similar to that regarding the smallest perimeter among equivalent figures.
Also, this conjecture is the inverse of the one regarding the largest volume amongst solids with the same area.
Consider the following cube, regular octahedron and sphere.
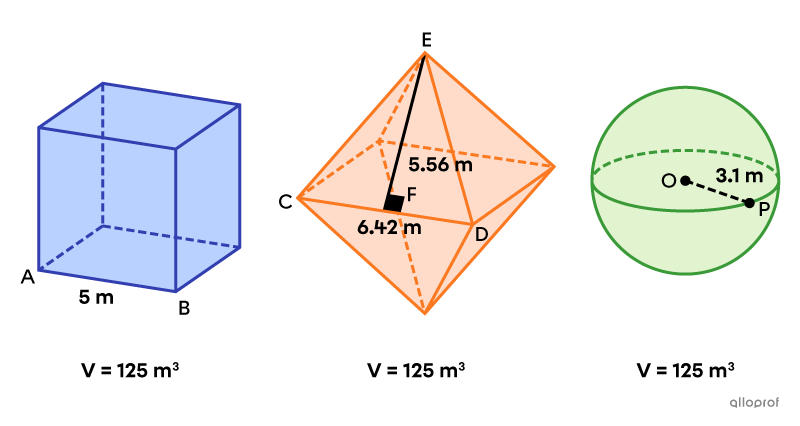
These three solids are equivalent since they all have a volume of |125\ \text{m}^3.| However, each has a different total area.
||\begin{align}A_\text{cube}&=6\left(\text{m}\overline{AB}\right)^2\\&=6\times5^2\\&=150\ \text{m}^2\end{align}||
Total area of the regular octahedron
All the faces of a regular octahedron are equilateral triangles. Since there are 8 faces, we can calculate the total area as follows:||\begin{align}A_\text{octahedron}&=8\left(\dfrac{\text{m}\overline{CD}\times\text{m}\overline{EF}}{2}\right)\\&=4\times6.42\times5.56\\&\approx142.78\ \text{m}^2\end{align}||
||\begin{align}A_\text{sphere}&=4\pi\left(\text{m}\overline{OP}\right)^2\\&=4\pi(3.1)^2\\&\approx120.76\ \text{m}^2\end{align}||
Therefore, amongst these 3 equivalent solids, the sphere has the smallest total area.