Des figures équivalentes sont des figures qui ont la même aire.
Des figures isométriques sont nécessairement des figures équivalentes.
Cependant, des figures équivalentes ne sont pas nécessairement des figures isométriques. En effet, 2 figures équivalentes peuvent être complètement différentes.
On peut démontrer que le triangle |\color{#333fb1}{ABC}| et le carré |\color{#fa7921}{IJKL}| suivants sont équivalents en calculant leur aire respective.
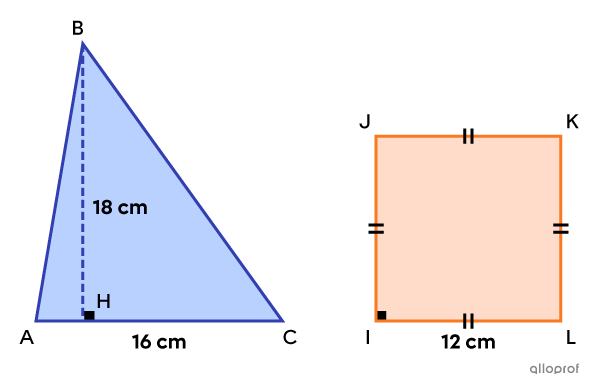
||\begin{align}A_\text{triangle}&=\dfrac{\text{m}\overline{AC}\times\text{m}\overline{BH}}{2}\\&=\dfrac{16\times18}{2}\\&=144\ \text{cm}^2\end{align}||
||\begin{align}A_\text{carré}&=\left(\text{m}\overline{IL}\right)^2\\&=12^2\\&=144\ \text{cm}^2\end{align}||
Conclusion : Le triangle |\color{#333fb1}{ABC}| et le carré |\color{#fa7921}{IJKL}| sont équivalents, puisqu’ils ont chacun une aire de |144\ \text{cm}^2.|
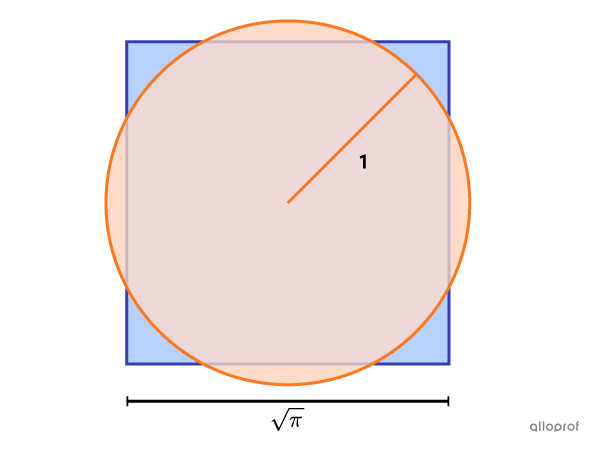
Considérée comme l’un des 3 grands problèmes des mathématiques de l’Antiquité, la quadrature du cercle porte sur les figures équivalentes. L’objectif de ce problème, dont on peut trouver la première trace écrite sur le célèbre papyrus Rhind d’Égypte, est de démontrer comment construire à la règle et au compas un carré dont l’aire est équivalente à celle d’un cercle donné.
C’est en 1882, après près de 3 000 ans, que le mathématicien allemand Ferdinand von Lindemann démontre que cette construction est impossible à accomplir.
Il est souvent nécessaire d'utiliser l'algèbre pour trouver des mesures manquantes dans des figures équivalentes. Voici la démarche à suivre pour y arriver.
-
Déterminer l'équation formée par l'équivalence entre l’aire des figures.
-
Résoudre l’équation.
-
Répondre à la question.
Voici un 1er exemple dans lequel il n’y a qu’une seule inconnue.
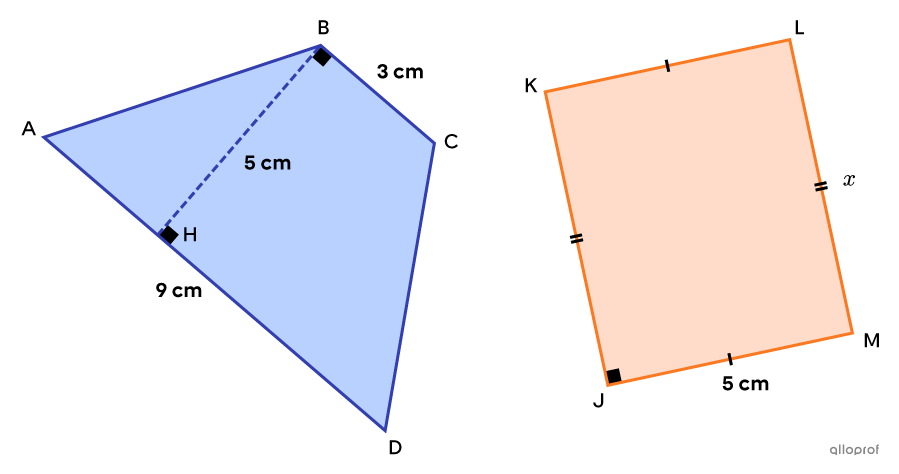
Trouve la hauteur du rectangle |\color{#fa7921}{JKLM},| sachant qu’il est une figure équivalente au trapèze |\color{#333fb1}{ABCD}.|
-
Déterminer l'équation formée par l'équivalence entre l’aire des figures
On commence par déterminer l’aire du trapèze et du rectangle selon les informations fournies.
||\begin{align}A_\text{trapèze}&=\dfrac{\left(\text{m}\overline{AD}+\text{m}\overline{BC}\right)\times\text{m}\overline{BH}}{2}\\&=\dfrac{(9+3)\times5}{2}\\&=30\ \text{cm}^2\end{align}||
||\begin{align}A_\text{rectangle}&=\text{m}\overline{JM}\times\text{m}\overline{LM}\\&=5x\end{align}||
On obtient alors l’équation suivante.||\begin{align}\color{#333fb1}{A_\text{trapèze}}&=\color{#fa7921}{A_\text{rectangle}}\\\color{#333fb1}{30}&=\color{#fa7921}{5x}\end{align}||
-
Résoudre l’équation
||\begin{align}\color{#ec0000}{\dfrac{\color{black}{30}}{5}}&=\color{#ec0000}{\dfrac{\color{black}{5x}}{5}}\\6\ \text{cm}&=x\end{align}|| -
Répondre à la question
La hauteur du rectangle |\color{#fa7921}{JKLM}| est de |6\ \text{cm}.|
Voici un 2e exemple dans lequel il y a plusieurs inconnues.
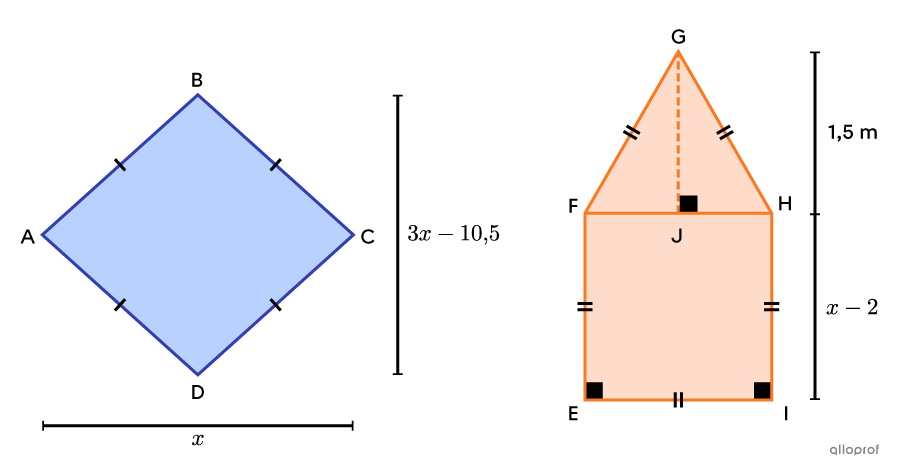
Trouve la hauteur du pentagone |\color{#fa7921}{EFGHI},| sachant qu’il est une figure équivalente au losange |\color{#333fb1}{ABCD}.|
-
Déterminer l'équation formée par l'équivalence entre l’aire des figures
On commence par déterminer l’aire du losange |\color{#333fb1}{ABCD}| et du pentagone |\color{#fa7921}{EFGHI}| selon les informations fournies. Remarque que le pentagone est une figure décomposable en un carré et un triangle équilatéral.
||\begin{align}A_\text{losange}&=\dfrac{\text{m}\overline{AC}\times\text{m}\overline{BD}}{2}\\&=\dfrac{x(3x-10{,}5)}{2}\end{align}||
Aire du pentagone décomposable
||\begin{align}A_\text{pentagone}&=A_\text{carré}+A_\text{triangle}\\&=\left(\text{m}\overline{HI}\right)^2+\dfrac{\text{m}\overline{HF}\times\text{m}\overline{JG}}{2}\\&=(x-2)^2+\dfrac{(x-2)\times1{,}5}{2}\end{align}||
On obtient alors l’équation suivante.||\begin{align}\color{#333fb1}{A_\text{losange}}&=\color{#fa7921}{A_\text{pentagone}}\\\color{#333fb1}{\dfrac{x(3x-10{,}5)}{2}}&=\color{#fa7921}{(x-2)^2+\dfrac{(x-2)\times1{,}5}{2}}\end{align}||
-
Résoudre l’équation
On multiplie d’abord les 2 membres de l’équation par |2| afin d’éliminer les fractions, puis on regroupe les termes semblables.
||\begin{align}\dfrac{x(3x-10{,}5)}{2}\color{#ec0000}{\times2}&=\color{#ec0000}{\left(\color{black}{(x-2)^2+\dfrac{1{,}5(x-2)}{2}}\right)\times2}\\x(3x-10{,}5)&=2(x-2)^2+1{,}5(x-2)\\3x^2-10{,}5x&=2(x^2-4x+4)+1{,}5x-3\\3x^2-10{,}5x&=2x^2-8x+8+1{,}5x-3\\x^2-4x-5&=0\end{align}||
Pour résoudre cette équation de degré 2, on peut utiliser de la formule quadratique.||\begin{align}x&=\dfrac{-b\pm\sqrt{b^2-4ac}}{2a}\\&=\dfrac{-(-4)\pm\sqrt{(-4)^2-4(1)(-5)}}{2(1)}\\&=\dfrac{4\pm\sqrt{36}}{2}\\\\x_1&=-1\ \text{m}\quad\text{et}\quad x_2=5\ \text{m}\end{align}||On doit rejeter la solution |x_1=-1\ \text{m}| puisque cela impliquerait, entre autres, que la mesure de la diagonale |\overline{AC}| du losange |\color{#333fb1}{ABCD}| soit négative. La solution recherchée est donc |x_2=5\ \text{m}.|
-
Répondre à la question
||\begin{align}h_\text{pentagone}&=\text{m}\overline{JG}+\text{m}\overline{HI}\\&=1{,}5+\color{#333fb1}{x}-2\\&=1{,}5+\color{#333fb1}{5}-2\\&=4{,}5\ \text{m}\end{align}||
Ainsi, la hauteur du pentagone |\color{#fa7921}{EFGHI}| est de |4{,}5\ \text{m}.|
Il est possible de dégager certaines conjectures concernant le périmètre de figures planes équivalentes. On examine plusieurs exemples pour vérifier que chacune de ces propositions est vraie.
Parmi tous les polygones équivalents à |n| côtés, c'est le polygone régulier qui possède le plus petit périmètre.
Cette conjecture est similaire à celle qui concerne la plus petite aire parmi les prismes équivalents.
Soit le rectangle |\color{#333fb1}{ABCD},| le cerf-volant |\color{#fa7921}{IJKL}| et le carré |\color{#7cca51}{EFGH}| suivants.
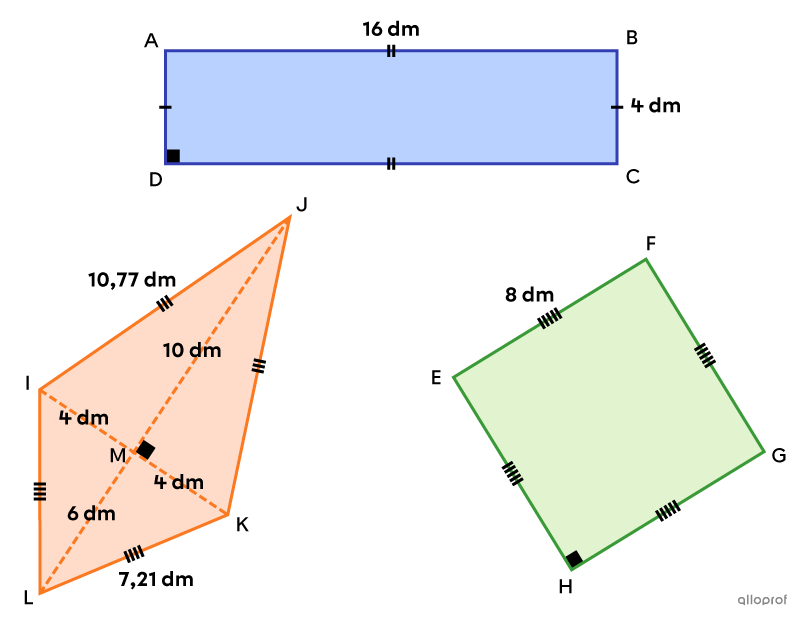
Ces 3 quadrilatères sont équivalents, puisqu’ils ont tous une aire de |64\ \text{dm}^2.|
||\begin{align}A_\text{rectangle}&=\text{m}\overline{AB}\times\text{m}\overline{BC}\\&=16\times 4\\&=64\ \text{dm}^2\end{align}||
||\begin{align}A_\text{cerf-volant} &=\dfrac{\text{m}\overline{IK}\times\text{m}\overline{JL}}{2}\\A_\text{cerf-volant}&=\dfrac{(4+4)\times(10+6)}{2}\\A_\text{cerf-volant}&=64\ \text{dm}^2\end{align}||
||\begin{align}A_\text{carré} &=\left(\text{m}\overline{EF}\right)^2\\&=8^2\\&=64\ \text{dm}^2\end{align}||
Toutefois, chaque périmètre est différent.
||\begin{align}P_\text{rectangle}&=2\times\text{m}\overline{AB}+2\times\text{m}\overline{BC}\\&=2\times16+2\times4\\&=40\ \text{dm}\end{align}||
||\begin{align}P_\text{cerf-volant}&=2\times\text{m}\overline{IJ}+2\times\text{m}\overline{KL}\\&=2\times10{,}77+2\times7{,}21\\&=35{,}96\ \text{dm}\end{align}||
||\begin{align}P_\text{carré}&=4\times\text{m}\overline{EF}\\&=4\times8\\&=32\ \text{dm}\end{align}||
Ainsi, parmi ces 3 quadrilatères équivalents, c'est le carré qui possède le plus petit périmètre, puisque c’est un polygone régulier à 4 côtés.
Parmi tous les polygones réguliers équivalents, c'est le polygone régulier ayant le plus grand nombre de côtés qui possède le plus petit périmètre.
Soit le pentagone régulier, l’hexagone régulier et l’heptagone régulier suivants.
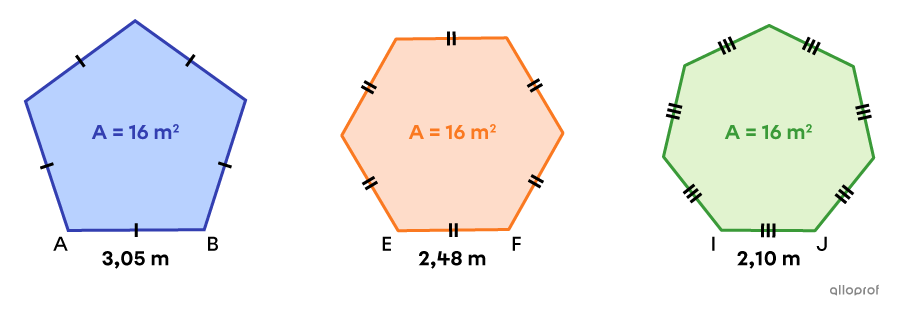
Périmètre du pentagone régulier
||\begin{align}P_\text{pentagone}&=n\times\text{m}\overline{AB}\\&=5\times3{,}05\\&=15{,}25\ \text{m}\end{align}||
Périmètre de l’hexagone régulier
||\begin{align}P_\text{hexagone}&=n\times\text{m}\overline{EF}\\&=6\times2{,}48\\&=14{,}88\ \text{m}\end{align}||
Périmètre de l’heptagone régulier
||\begin{align}P_\text{heptagone}&=n\times\text{m}\overline{EF}\\&=7\times2{,}10\\&=14{,}70\ \text{m}\end{align}||
Ainsi, parmi ces 3 polygones réguliers équivalents, c'est l’heptagone régulier qui possède le plus petit périmètre, puisque c’est celui qui a le plus grand nombre de côtés.
Parmi toutes les figures planes équivalentes, c'est le disque qui possède le plus petit périmètre.
Cette conjecture est similaire à celle qui concerne la plus petite aire parmi les solides équivalents.
Soit le parallélogramme |\color{#333fb1}{ABCD},| le triangle |\color{#fa7921}{EFG}| et le disque de rayon |\color{#7cca51}{OI}| suivants.
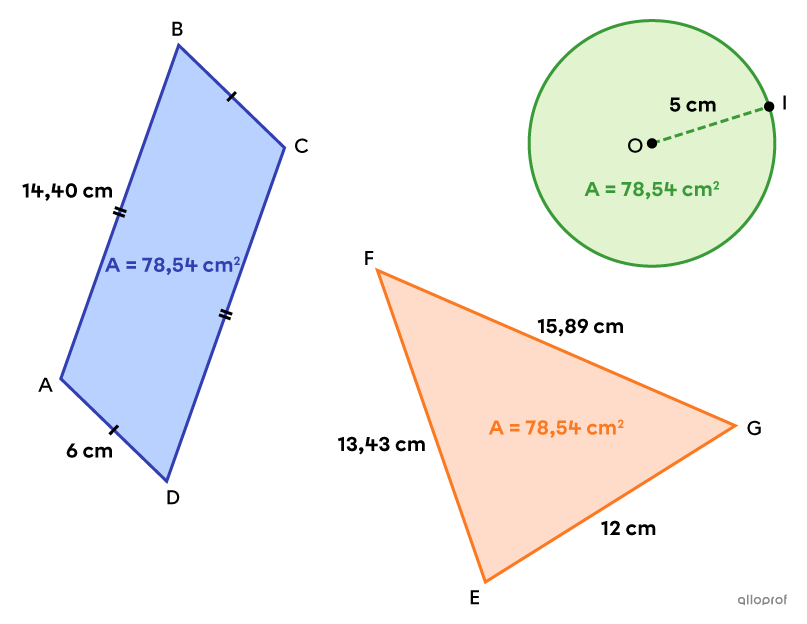
Ces 3 figures sont équivalentes, puisqu’elles ont toutes une aire de |78{,}54\ \text{cm}^2.| Toutefois, chaque périmètre est différent.
||\begin{align}P_\text{triangle}&=\text{m}\overline{EF}+\text{m}\overline{FG}+\text{m}\overline{GE}\\&=13{,}43+15{,}89+12\\&=41{,}32\ \text{cm}\end{align}||
||\begin{align}P_\text{parallélogramme}&=2\times\text{m}\overline{DA}+2\times\text{m}\overline{AB}\\&=2\times6+2\times14{,}40\\&=40{,}80\ \text{cm}\end{align}||
||\begin{align}C_\text{disque}&=2\pi\times\text{m}\overline{OI}\\&=2\pi\times5\\&\approx31{,}42\ \text{cm}\end{align}||
Ainsi, parmi ces 3 figures planes équivalentes, c'est le disque qui possède le plus petit périmètre.
L’animation interactive suivante résume les 3 conjectures précédentes.
En déplaçant le curseur Nombre de côtés |(n),| on peut voir que plus le nombre de côtés augmente, plus le périmètre |(P)| diminue vers une certaine valeur. Cette valeur correspond à la circonférence du cercle équivalent à tous ces polygones réguliers.
On peut démontrer une relation algébrique qui donne le périmètre d’un polygone régulier en fonction de son aire.
|P=2\sqrt{A\times n\times\tan\dfrac{180^\circ}{n}}|
où
|P :| périmètre du polygone régulier
|A :| aire du polygone régulier
|n :| nombre de côtés du polygone régulier
Comme on peut le voir dans l’animation interactive précédente, tous les polygones réguliers à |n| côtés sont décomposables en |n| triangles isocèles isométriques. On prend le pentagone régulier comme exemple particulier pour définir d’abord chacune des variables.
|c :| côté
|a :| apothème
|\theta :| angle au centre
Le périmètre |(P)| et l’aire |(A)| d’un polygone régulier sont donnés par les expressions suivantes.||\begin{align}P&=n\times c\\\\A&=\dfrac{c\times a\times n}{2}\end{align}||
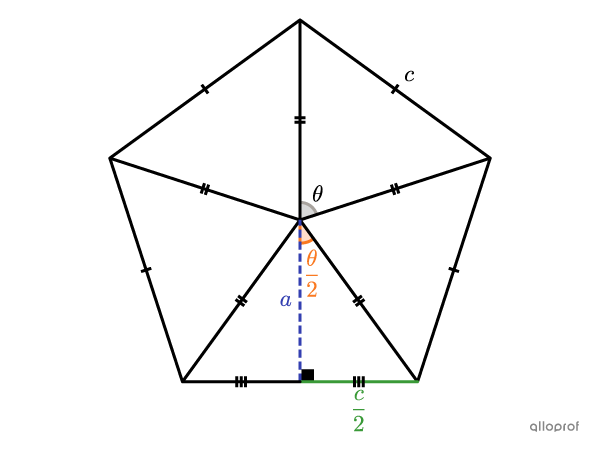
On isole |c| dans l’équation de l’aire afin de procéder à une substitution dans l’équation du périmètre.||\begin{align}A&=\dfrac{c\times a\times n}{2}\\2A&=c\times a\times n\\\dfrac{2A}{a\times n}&=c\\\\P&=n\times\color{#7cca51}{c}\\P&=n\times\color{#7cca51}{\dfrac{2A}{a\times n}}\\P&=\dfrac{2A}{a}\end{align}||Cette équation donne le périmètre d’un polygone régulier en fonction de son aire |(A)| et de son apothème |(a).| À l’aide du rapport tangente dans le triangle rectangle, qui correspond à la moitié du triangle isocèle, on peut établir une relation entre l’apothème, la moitié du côté et la moitié de l’angle au centre du polygone.||\begin{align}\tan\color{#fa7921}{\dfrac{\theta}{2}}&=\dfrac{\color{#7cca51}{\dfrac{c}{2}}}{\color{#333fb1}{a}}\\a\times\tan\dfrac{\theta}{2}&=\dfrac{c}{2}\\a&=\dfrac{c}{2\tan\frac{\theta}{2}}\end{align}||On substitue |c| par la même expression que plus tôt, puis on isole |a.|||\begin{align}a&=\dfrac{\color{#7cca51}{c}}{2\tan\frac{\theta}{2}}\\a&=\dfrac{\color{#7cca51}{\dfrac{2A}{a\times n}}}{2\tan\frac{\theta}{2}}\\a&=\dfrac{2A}{a\times n}\times\dfrac{1}{2\tan\frac{\theta}{2}}\\a&=\dfrac{A}{a\times n\times\tan\frac{\theta}{2}}\\a^2&=\dfrac{A}{n\times\tan\frac{\theta}{2}}\\a&=\sqrt{\dfrac{A}{n\times\tan\frac{\theta}{2}}}\end{align}||On substitue |a| dans l’équation du périmètre par l’expression qu’on vient de trouver, puis on simplifie.||\begin{align}P&=\dfrac{2A}{\color{#333fb1}{a}}\\ P&=\dfrac{2A}{\color{#333fb1}{\sqrt{\dfrac{A}{n\times\tan\frac{\theta}{2}}}}}\\ P&=2A\times\sqrt{\dfrac{n\times\tan\frac{\theta}{2}}{A}}\\P&=2\sqrt{A^2\times\dfrac{n\times\tan\frac{\theta}{2}}{A}}\\P&=2\sqrt{A\times n\times\tan\frac{\theta}{2}}\end{align}||Finalement, on substitue |\theta| par l’expression de l’angle au centre d’un polygone régulier.||\begin{align}P&=2\sqrt{A\times n\times\tan\frac{\color{#fa7921}{\theta}}{2}}\\P&=2\sqrt{A\times n\times\tan\dfrac{\color{#fa7921}{\frac{360^{\circ}}{n}}}{2}}\\P&=2\sqrt{A\times n\times\tan\dfrac{180^{\circ}}{n}}\end{align}||