Comme pour les figures isométriques et semblables, il est possible de vérifier si 2 solides sont isométriques ou semblables en vérifiant si leurs segments homologues ou leurs faces homologues sont le résultat des mêmes transformations géométriques.
-
Des arêtes homologues sont des segments qui ont le même rôle dans des solides différents.
-
Des faces homologues sont des surfaces qui ont le même rôle dans des solides différents.
-
Des angles homologues sont des angles qui ont le même rôle dans des solides différents.
Cette image montre quelques exemples.
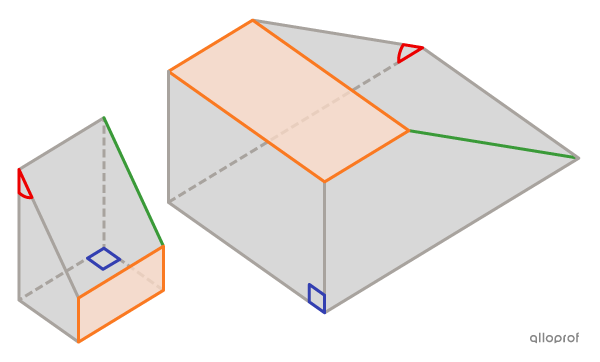
Le mot isométrie prend son origine dans la Grèce antique. Ce mot est formé de iso, qui signifie même, et de métrie, qui signifie mesure.
On dit que 2 solides sont isométriques si toutes leurs arêtes homologues et tous leurs angles homologues sont isométriques.
Pour savoir si 2 solides sont isométriques, on peut démontrer que l’un d’eux (le solide image) est le résultat d’une ou de plusieurs transformations géométriques à partir de l’autre (le solide initial). Ces transformations géométriques sont les suivantes.
Voici un exemple où plusieurs transformations géométriques sont nécessaires pour démontrer que 2 solides sont isométriques.
À l’aide des curseurs Translation et Rotation dans l’animation interactive suivante, on peut démontrer, par la translation, puis par la rotation, que le cône orange est isométrique au cône rouge.
Par une translation de |4| unités suivie d’une rotation de |180^\circ| par rapport au point |O,| on observe que le cône rouge se superpose parfaitement avec le cône orange. Ceci implique que toutes les arêtes homologues et tous les angles homologues sont isométriques. On peut donc conclure que ces 2 cônes sont isométriques.
On dit que 2 solides sont congruents lorsque la figure image est le résultat d’un déplacement, c’est-à-dire d’une translation et/ou d’une rotation seulement. On privilégie donc l’utilisation du mot isométrique, puisqu’on inclut aussi la réflexion qui n’est pas un déplacement, mais bien un retournement.
Il est possible de démontrer que 2 solides sont isométriques autrement que par les transformations géométriques. En effet, si leurs angles homologues et leurs arêtes homologues sont isométriques, alors les solides sont nécessairement isométriques.
Voici un exemple où on utilise cette méthode pour démontrer que 2 solides sont isométriques.
Parmi les prismes droits à base carrée suivants, identifie celui qui est isométrique au cube bleu.

On doit comparer les angles et les arêtes du cube bleu aux angles homologues et aux arêtes homologues de chaque solide.
-
Comparaison avec le solide orange
Arêtes homologues
Le solide orange n’est pas un cube, car il possède des arêtes de |5\ \text{dm}| et de |5{,}01\ \text{dm}.|
Ainsi, les arêtes homologues du cube bleu et du solide orange ne sont pas isométriques.
Angles homologues
Tous les angles du solide orange sont des angles droits, puisqu’il s’agit d’un prisme droit à base carrée.
Ainsi, les angles homologues du cube bleu et du solide orange sont isométriques.
Conclusion
Le cube bleu et le solide orange ne sont pas isométriques.
-
Comparaison avec le solide vert
Arêtes homologues
Le solide vert est un cube, car il s’agit d’un prisme droit à base carrée dont les arêtes n’appartenant pas à la base sont isométriques. On peut alors déterminer la mesure de ses arêtes à partir de son volume.||\begin{align}V&=c^3\\\color{#ec0000}{\sqrt[3]{\color{black}{150}}}&=\color{#ec0000}{\sqrt[3]{\color{black}{c^3}}}\\5{,}31\ \text{dm}&\approx c\end{align}||Ainsi, les arêtes homologues du cube bleu et du solide vert ne sont pas isométriques.
Angles homologues
Tous les angles du solide vert sont des angles droits, puisqu’il s’agit d’un cube.
Ainsi, les angles homologues du cube bleu et du solide vert sont isométriques.
Conclusion
Le cube bleu et le solide vert ne sont pas isométriques.
-
Comparaison avec le solide rouge
Arêtes homologues
Le solide rouge est un cube, car il s’agit d’un prisme droit à base carrée dont les arêtes n’appartenant pas à la base sont isométriques. On peut alors déterminer la mesure de ses arêtes à partir de son aire totale.||\begin{align}A_T&=6c^2\\\color{#ec0000}{\dfrac{\color{black}{150}}{6}}&=\color{#ec0000}{\dfrac{\color{black}{6c^2}}{6}}\\\color{#ec0000}{\sqrt{\color{black}{25}}}&=\color{#ec0000}{\sqrt{\color{black}{c^2}}}\\5\ \text{dm}&=c\end{align}||Ainsi, les arêtes homologues du cube bleu et du solide rouge sont isométriques.
Angles homologues
Tous les angles du solide rouge sont des angles droits puisqu’il s’agit d’un cube.
Ainsi, les angles homologues du cube bleu et du solide rouge sont isométriques.
Conclusion
Le cube bleu et le solide rouge sont isométriques.
Réponse : Le cube bleu est isométrique au cube rouge, car leurs angles homologues et leurs arêtes homologues sont isométriques.
Des solides isométriques sont nécessairement des solides qui ont la même aire totale et un volume équivalent.
Cependant, des solides équivalents ou de même aire ne sont pas nécessairement des solides isométriques.
On dit que 2 solides sont semblables si leurs arêtes homologues sont proportionnelles et si leurs angles homologues sont isométriques.
Pour savoir si 2 solides sont semblables, on peut démontrer que l’un d’eux (le solide image) est le résultat d’une homothétie à partir de l’autre (le solide initial).
Dans l’animation interactive suivante, on peut déplacer le curseur Rapport d’homothétie afin de voir que les 3 pyramides sont semblables par rapport au centre d’homothétie |O.|
Lorsque le rapport d’homothétie vaut |2,| chaque arête de la pyramide bleue mesure le double de son arête homologue dans la pyramide mauve. Lorsque le rapport d’homothétie vaut |0{,}5,| chaque arête de la pyramide verte mesure la moitié de son arête homologue dans la pyramide mauve.
Concernant les angles homologues, ils sont tous isométriques, peu importe la valeur du rapport d’homothétie.
Il arrive parfois que l’homothétie ne soit pas suffisante pour démontrer la similitude, c’est-à-dire qu’il est aussi nécessaire d’utiliser la translation, la rotation et/ou la réflexion.
Il est possible de démontrer que 2 solides sont semblables autrement que par l’homothétie. En effet, si leurs angles homologues sont isométriques et toutes leurs arêtes homologues sont proportionnelles, alors les solides sont nécessairement semblables.
Sans tenir compte du signe, le rapport d’homothétie est équivalent au rapport entre les arêtes homologues, c’est-à-dire le rapport de similitude |\boldsymbol{(k)}.|
De plus, si 2 solides sont semblables, tous les rapports |k| sont égaux et les relations entre les rapports de similitude, d’aires et de volumes sont respectées.
Voici un exemple où on utilise cette méthode pour démontrer que 2 solides sont semblables.
Détermine si les prismes droits à base rectangulaire suivants sont semblables ou non.
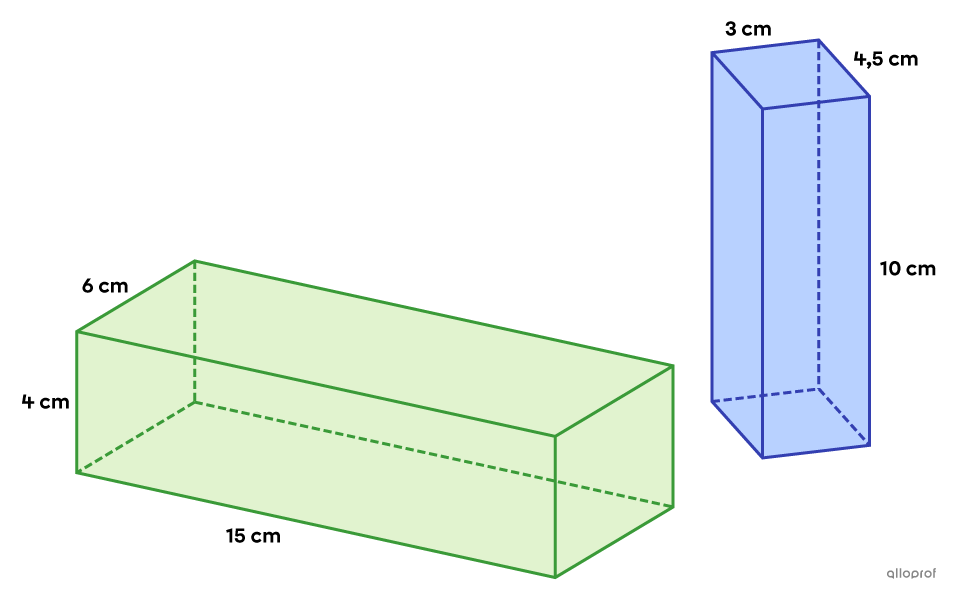
Pour déterminer si les 2 prismes sont semblables, on calcule le rapport de similitude |(\boldsymbol{k})| entre les paires d’arêtes homologues. Afin de bien identifier les paires d’arêtes homologues, on peut se baser sur leur longueur. On doit former une paire avec les arêtes ayant la plus petite mesure au sein de leur prisme respectif, une autre paire avec celles ayant une mesure moyenne, et une autre paire avec celles ayant la plus grande mesure.
Angles homologues
Les 2 solides sont des prismes droits à base rectangulaire, ce qui implique que tous les angles mesurent |90^\circ.|
Arêtes moyennes||\begin{align}k&=\dfrac{\color{#3a9a38}{\text{Arête moyenne du prisme vert}}}{\color{#333fb1}{\text{Arête moyenne du prisme bleu}}}\\k&=\dfrac{\color{#3a9a38}{6\ \text{cm}}}{\color{#333fb1}{4{,}5\ \text{cm}}}=\dfrac{6\color{#ec0000}{\times2}}{4{,}5\color{#ec0000}{\times2}}=\dfrac{12\color{#ec0000}{\div3}}{9\color{#ec0000}{\div3}}\\k&=\dfrac{4}{3}\end{align}||
Petites arêtes||\begin{align}k&=\dfrac{\color{#3a9a38}{\text{Petite arête du prisme vert}}}{\color{#333fb1}{\text{Petite arête du prisme bleu}}}\\k&=\dfrac{\color{#3a9a38}{4\ \text{cm}}}{\color{#333fb1}{3\ \text{cm}}}=\dfrac{4}{3}\end{align}||
Grandes arêtes||\begin{align}k&=\dfrac{\color{#3a9a38}{\text{Grande arête du prisme vert}}}{\color{#333fb1}{\text{Grande arête du prisme bleu}}}\\k&=\dfrac{\color{#3a9a38}{15\ \text{cm}}}{\color{#333fb1}{10\ \text{cm}}}=\dfrac{15\color{#ec0000}{\div5}}{10\color{#ec0000}{\div5}}=\dfrac{3}{2}\end{align}||
Conclusion : Le prisme vert et le prisme bleu ne sont pas semblables, car les rapports d’arêtes homologues ne sont pas tous égaux.