As with isometric (congruent) and similar figures, it is possible to verify whether 2 solids are isometric or similar by checking if their corresponding segments or corresponding faces are the result of the same geometric transformations.
-
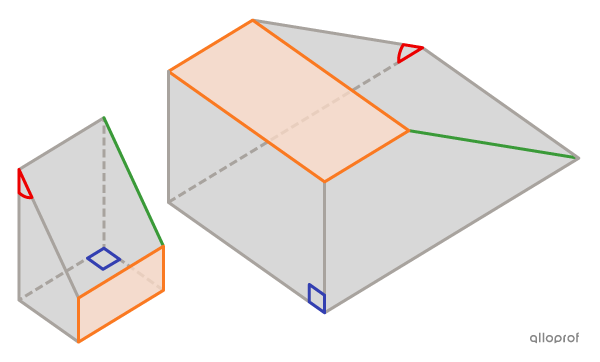
Corresponding edges are segments that share the same position in different solids.
-
Corresponding faces are surfaces that share the same position in different solids.
-
Corresponding angles are angles that share the same position in different solids.
This image shows some examples.
The word isometry has its origin in ancient Greece. This word is composed of iso, meaning same, and metry, meaning measure.
Two solids are isometric if all their corresponding edges and corresponding angles are isometric (congruent).
To determine if 2 solids are isometric, we can show that one of them (the image solid) is the result of one or more geometric transformations from the other (the initial solid). The geometric transformations are as follows:
Here is an example where several geometric transformations are needed to prove that the 2 solids are isometric.
Using the Translation and Rotation sliders in the interactive animation below, we can prove, first with a translation and then with a rotation, that the orange cone is isometric to the red cone.
A translation of |4| units followed by a rotation of |180^\circ| about point |O| proves that the red cone perfectly overlaps the orange cone. This means that all the corresponding edges and corresponding angles are isometric. Therefore, these 2 cones are isometric.
Two solids are said to be congruent when the image figure results from a displacement, meaning translation and/or rotation. The word isometric is preferred since it also includes the reflection, in which an object is flipped, not just displaced.
It is possible to prove that 2 solids are isometric using other methods than geometric transformations. If the corresponding angles and edges are isometric, the solids are necessarily isometric.
Here is an example of using this method to prove that 2 solids are isometric.
Identify which of the following square-based prisms is isometric to the blue cube.
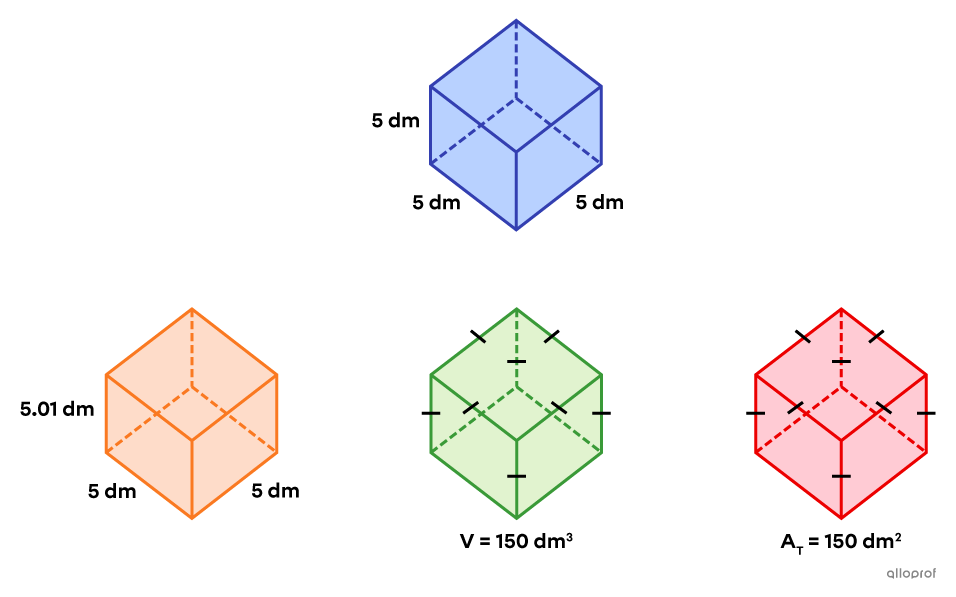
Compare the angles and edges of the blue cube with the corresponding angles and corresponding edges of each solid.
-
Comparison with the orange solid
Corresponding edges
The orange solid is not a cube because it has edges that measure |5\ \text{dm}| and others that measure |5.01\ \text{dm}.|
Therefore, the corresponding edges of the blue cube and the orange solid are not isometric.
Corresponding angles
All the angles of the orange solid are right angles since it is a square-based right prism.
Therefore, the corresponding angles of the blue cube and the orange solid are isometric.
Conclusion
The blue cube and the orange solid are not isometric.
-
Comparison with the green solid
Corresponding edges
The green solid is a cube because it is a square-based right prism and the edges that are not part of the base are isometric. The measure of its edges can be found from its volume.||\begin{align}V&=s^3\\\color{#ec0000}{\sqrt[3]{\color{black}{150}}}&=\color{#ec0000}{\sqrt[3]{\color{black}{s^3}}}\\5.31\ \text{dm}&\approx s\end{align}||Therefore, the corresponding edges of the blue cube and the green solid are not isometric.
Corresponding angles
All of the angles of the green solid are right angles since it is a cube.
Therefore, the corresponding angles of the blue cube and the green solid are isometric.
Conclusion
The blue cube and the green solid are not isometric.
-
Comparison with the red solid
Corresponding edges
The red solid is a cube because it is a square-based right prism and the edges that are not part of the base are isometric. The measure of its edges can be found from its surface area.||\begin{align}A_T&=6s^2\\\color{#ec0000}{\dfrac{\color{black}{150}}{6}}&=\color{#ec0000}{\dfrac{\color{black}{6s^2}}{6}}\\\color{#ec0000}{\sqrt{\color{black}{25}}}&=\color{#ec0000}{\sqrt{\color{black}{s^2}}}\\5\ \text{dm}&=s\end{align}||Therefore, the corresponding edges of the blue cube and the red solid are isometric.
Corresponding angles
All of the angles of the red solid are right angles since it is a cube.
Therefore, the corresponding angles of the blue cube and the red solid are isometric.
Conclusion
The blue cube and the red solid are isometric.
Answer: The blue cube is isometric to the red cube, because both their corresponding angles and corresponding edges are isometric.
Isometric solids are solids that necessarily have the same surface area and equivalent volume.
However, not all solids that are equivalent or have the same area are necessarily isometric solids.
Two solids are said to be similar if their corresponding edges are proportional and if their corresponding angles are isometric.
To determine if 2 solids are similar, we can show that one of them (the image solid) is the result of a dilation of the other (the initial solid).
In the following interactive animation, move the scale factor slider to see that the 3 pyramids are similar in relation to the dilation centre |O.|
When the scale factor is |2,| the measure of each edge in the blue pyramid is twice the length of its corresponding edge in the purple pyramid. When the scale factor is |0.5,| each edge of the green pyramid is half the length of its corresponding edge in the purple pyramid.
Corresponding angles are always congruent regardless of the value of the scale factor.
Sometimes a dilation is not enough to prove similarity. In other words, sometimes it is necessary to also use translations, rotations and/or reflections.
It is possible to prove that 2 solids are similar using a method other than using a dilation. If the corresponding angles are congruent and all the corresponding edges are proportional, then the solids are necessarily similar.
Regardless of the sign, the scale factor is equivalent to the ratio between corresponding edges, or the similarity ratio |\boldsymbol{(k)}.|
Moreover, if 2 solids are similar, all of these |k| ratios are equal and the relationships between the similarity ratios, areas and volumes are respected.
Here is an example where this method is used to prove that 2 solids are similar.
Determine if the following rectangular-based right prisms are similar.
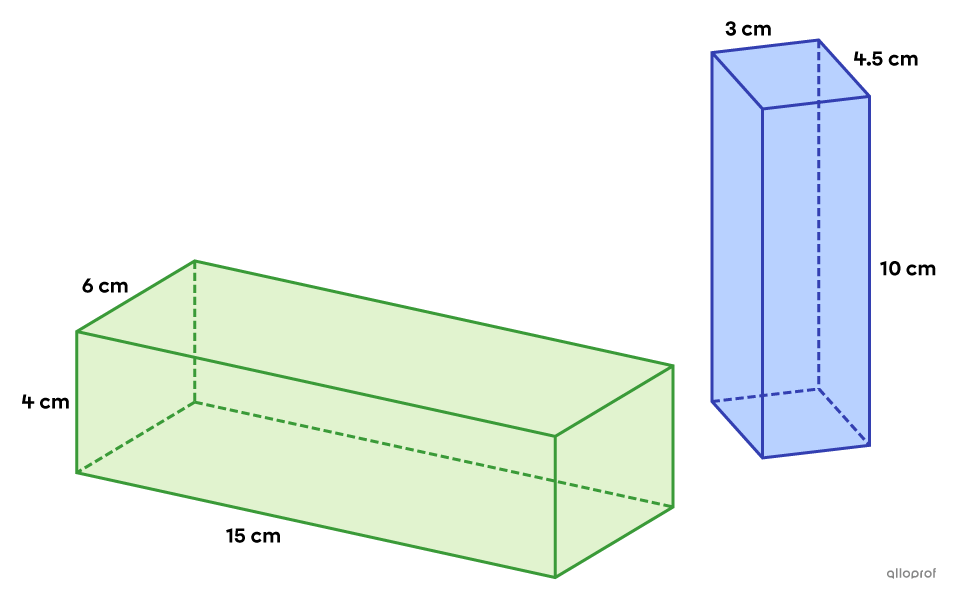
To determine if the 2 prisms are similar, calculate the similarity ratio (scale factor) |(k)| between the pairs of corresponding edges. To identify the pairs of corresponding edges, we can use their lengths as a guide. We can form one pair with the shortest edges within their respective prism, another pair with the middle edges and another pair with the longest edges.
Corresponding angles
The 2 solids are rectangular-based right prisms, which implies that all angles measure |90^\circ.|
Shortest edges||\begin{align}k&=\dfrac{\color{#3a9a38}{\text{Shortest edge of the green prism}}}{\color{#333fb1}{\text{Shortest edge of the blue prism}}}\\k&=\dfrac{\color{#3a9a38}{4\ \text{cm}}}{\color{#333fb1}{3\ \text{cm}}}=\dfrac{4}{3}\end{align}||
Medium edges||\begin{align}k&=\dfrac{\color{#3a9a38}{\text{Medium edge of the green prism}}}{\color{#333fb1}{\text{Medium edge of the blue prism}}}\\k&=\dfrac{\color{#3a9a38}{6\ \text{cm}}}{\color{#333fb1}{4.5\ \text{cm}}}=\dfrac{6\color{#ec0000}{\times2}}{4.5\color{#ec0000}{\times2}}=\dfrac{12\color{#ec0000}{\div3}}{9\color{#ec0000}{\div3}}\\k&=\dfrac{4}{3}\end{align}||
Longest edges||\begin{align}k&=\dfrac{\color{#3a9a38}{\text{Longest edge of the green prism}}}{\color{#333fb1}{\text{Longest edge of the blue prism}}}\\k&=\dfrac{\color{#3a9a38}{15\ \text{cm}}}{\color{#333fb1}{10\ \text{cm}}}=\dfrac{15\color{#ec0000}{\div5}}{10\color{#ec0000}{\div5}}=\dfrac{3}{2}\end{align}||
Conclusion: The green prism and the blue prism are not similar because not all of their corresponding edges are proportional (their ratios are not all equal).