Voici un guide de préparation aux examens de fin d'année contenant toutes les notions abordées au premier cycle du secondaire. Pour expliquer le tout, chaque notion sera suivie d'un exemple et d'un lien qui mène à une fiche de notre bibliothèque virtuelle.
Pour être en mesure de comparer des nombres, il est préférable d'utiliser un seul type d'écriture. Puisque l'ensemble des |\mathbb{Q}| est celui qui contient le plus d'éléments dont on peut facilement illustrer la valeur, l'écriture en notation fractionnaire |\left( \dfrac{a}{b} \right)| avec |b \neq 0| sera utilisée.
Place les nombres suivants en ordre croissant :
|4\dfrac{1}{3}\ ,| |\color{blue}{\dfrac{8}{3}}\ ,| |\color{red}{ -0{,}625}\ ,| |\color{green}{-80\ \%}\ ,| |\color{fuchsia}{\left( \dfrac{-1}{2} \right) ^2}\ ,| |\color{orange}{\sqrt9}|
| CALCULS | JUSTIFICATIONS |
|---|---|
|
|\displaystyle 4\frac{1}{3} = \frac{4 \times 3 + 1}{3} = \frac{13}{3}| |\color{blue}{\displaystyle \frac{8}{3}}| |\color{red}{\displaystyle -0,625 = \frac{-625}{1000} = \frac{-5}{8}}| |\color{green}{\displaystyle -80\%=\frac{-80}{100} = \frac{-4}{5}}| |\color{fuchsia}{\displaystyle \left( \frac{-1}{2} \right)^2 = \frac{-1}{2} \times \frac{-1}{2} = \frac{1}{4}}| |\displaystyle \color{orange}{\sqrt9 = 3}| |
Utiliser la notation fractionnaire réduite pour représenter chacune des quantités. |
|
|\displaystyle \frac{13}{3} = \frac{1040}{240}| |\color{blue}{\displaystyle \frac{8}{3}=\frac{640}{240}}| |\color{red}{\displaystyle \frac{-5}{8}=\frac{-150}{240}}| |\color{green}{\displaystyle \frac{-4}{5}=\frac{-192}{240}}| |\color{fuchsia}{\displaystyle \frac{1}{4}=\frac{60}{240}}| |\color{orange}{\displaystyle 3=\frac{3}{1} = \frac{720}{240}}| |
Écrire tous les nombres en utilisant un dénominateur commun. |
|
Puisque les dénominateurs sont tous égaux, on peut classer ces nombres seulement selon leur numérateur : |\displaystyle \color{white}{=}\color{green}{\frac{-192}{240}} < \color{red}{\frac{-150}{240}} < \color{fuchsia}{\frac{60}{240}} < \color{blue}{\frac{640}{240}} < \color{orange}{\frac{720}{240}} < \frac{1040}{240}| |
|
À voir aussi
Dans un problème écrit, il est important de bien comprendre la mise en situation afin d'orienter sa démarche de la bonne façon. Ainsi, il est utile de suivre ces étapes :
-
Créer la chaine d'opérations en ciblant les mots clés
-
Résoudre en suivant la priorité des opérations
Afin de s'assurer qu'il s'est bien préparé pour son évaluation de vendredi, Sylvain veut savoir pendant combien de minutes il a étudié. Lundi, il a étudié la moitié du temps par rapport à mardi. Mardi, il avait le nez dans ses livres de 18 h 30 à 19 h 20. Mercredi, il a passé 20 minutes de moins que la somme des deux jours précédents à lire ses notes. Pour sa dernière journée de préparation, il a passé le triple du temps de lundi à réviser ses travaux.
Au total, combien de minutes Sylvain a-t-il passé à étudier pour son évaluation?
| CALCULS | JUSTIFICATIONS |
|---|---|
|
Total |=| Lundi + Mardi + Mercredi + Jeudi |
Écrire la chaine d'opérations à résoudre. |
|
|\color{white}{\text{Total}}=\color{blue}{\displaystyle \left( \frac{50}{2}\right)} + \color{red}{50} + \color{orange}{\left(\left(50 + \displaystyle \frac{50}{2}\right) - 20\right)} + \color{fuchsia}{3 \times \displaystyle \left( \frac{50}{2}\right)}| |
Remplacer chaque journée par sa valeur respective. |
|
|\color{white}{\text{Total}}=\color{blue}{25} + \color{red}{50} + \color{orange}{\left(\left(50 + \displaystyle \frac{50}{2}\right) - 20\right)} + \color{fuchsia}{3 \times \displaystyle \left( \frac{50}{2}\right)}| |
Résoudre en suivant la priorité des opérations. |
|
Sylvain a passé |205| minutes à se préparer pour son évaluation. |
|
À voir aussi
| Un nombre est divisible par... | si... |
|---|---|
| 2 | le chiffre des unités est pair. |
| 3 | la somme de tous les chiffres du nombre est divisible par 3. |
| 4 | le nombre formé par les deux derniers chiffres est divisible par 4. |
| 5 | le chiffre des unités est 0 ou 5. |
| 6 | le nombre est divisible à la fois par 2 et par 3. |
| 8 | le nombre formé par ses 3 derniers chiffres est divisible par 8 ou lorsque le nombre est divisible par 4 et par 2. |
| 9 | la somme de ses chiffres est divisible par 9. |
| 10 | le chiffre des unités est 0. |
| 12 | le nombre est divisible à la fois par 3 et par 4. |
| 25 | le nombre se termine par 00, 25, 50 ou 75. |
À la suite de la tournée du quartier lors de la soirée d'Halloween, Judith et son fils Justin ont amassé une impressionnante quantité de bonbons. Après une semaine et quelques maux de ventre, ils en ont tellement mangé qu'ils souhaitent faire don de ce qu'il reste. Avec la fête de Justin qui s'en vient, Judith a la bonne idée de distribuer également le reste des |264| bonbons à chacun des amis de Justin qui seront présents pour l'occasion.
Si Judith permet à Justin d'inviter |9| amis, est-ce qu'elle pourra mettre son plan à exécution? Sinon, suggère un nombre raisonnable d'invités qui lui permettrait de se débarrasser de ses bonbons de façon égale, et ce, à tout le monde.
|
CALCULS |
JUSTIFICATIONS |
|---|---|
|
|264 \Rightarrow 2 + 6 + 4 = 12| |
Déterminer si |264| se divise par |9.| |
|
|264 \Rightarrow 64 \div 4 = 16| |
Trouver un diviseur de |264| qui est près de |9.| |
|
Judith devrait plutôt autoriser Justin à inviter |8| de ses amis. |
|
À voir aussi
La notion de pourcentage est un exemple de situation qui est toujours proportionnelle. Par contre, il faut être en mesure de bien construire la proportion afin de trouver les quantités voulues :
-
Identifier la quantité donnée et lui associer son pourcentage.
-
Identifier la quantité que l'on cherche et lui associer son pourcentage.
-
Construire adéquatement la proportion selon le modèle suivant : ||\displaystyle \frac{\color{red}{\text{Quantité donnée}}}{\color{blue}{\text{Quantité que l'on cherche}}} = \frac{\color{red}{\text{Son pourcentage}}}{\color{blue}{\text{Son pourcentage}}}||
-
Résoudre la situation de proportionnalité.
Afin de profiter de la vente de fin de saison dans un magasin de sport, Mme Caron s'est procuré quelques accessoires de vélo. En appliquant un rabais de |\color{red}{45\ \%},| elle a pu obtenir ce qu'elle cherchait pour seulement |\color{red}{14{,}85\ $}| (taxes incluses)!
Quel était le prix avant réduction (taxes incluses) de ses achats?
| CALCULS | JUSTIFICATIONS |
|---|---|
|
|\begin{align} \color{red}{\text{Quantité donnée}} &= \color{red}{\text{Son pourcentage}} \\ \color{red}{14{,}85 \ $} &= \color{red}{100\ \% - 45\ \%} \\ \color{red}{14{,}85\ $} &= \color{red}{55\ \%} \end{align}| |
Identifier la quantité donnée et lui associer son pourcentage. |
|
|\begin{align} \color{blue}{\text{Quantité que l'on cherche}} &= \color{blue}{\text{Son pourcentage}}\\ \color{blue}{\text{Prix avant réduction}} &= \color{blue}{100\ \%} \end{align}| |
Identifier la quantité que l'on cherche et son pourcentage. |
|
|\Rightarrow \displaystyle \frac{\color{red}{14{,}85 \ $}}{\color{blue}{\text{Prix avant réduction}}} = \frac{\color{red}{55\ \%}}{\color{blue}{100\ \%}}| |
Construire la proportion. |
|
|\begin{align} \color{blue}{\text{Prix avant réduction}} &= \displaystyle \frac{\color{blue}{100\ \%}\times \color{red}{14{,}85\ \ $}}{\color{red}{55\ \%}} \\ \color{blue}{\text{Prix avant réduction}} &= \color{blue}{27\ $} \end{align}| |
Résoudre la proportion. |
|
Avant l'application du rabais, elle aurait dû payer |27\ $| pour ses achats. |
|
À voir aussi
On exprime un rapport à l'aide de deux points superposés ou à l'aide d'une fraction.
|a : b| est le rapport partie par partie
|\displaystyle \frac{a}{a+b}| est le rapport partie-tout
où |a| et |b| sont des parties de même nature d'un tout et généralement premiers entre eux (rapport simplifié)
Par définition, les parties |a| et |b| d'un rapport |a:b| sont de même nature. Ainsi, on évite d'inscrire les unités associées à chacune des parties.
Lors d'une compétition sportive professionnelle, la bourse de |5\ 000\ $| a été séparée entre l'équipe championne et l'équipe finaliste. Lors de la remise des chèques, l'équipe victorieuse s'est méritée un montant de |\color{red}{3\ 500\ \$}| alors que le reste a été empoché par l'équipe terminant en deuxième position.
Ainsi, quel est le rapport associé au partage de la bourse avec l'équipe championne par rapport à l'équipe finaliste?
| CALCULS | JUSTIFICATIONS |
|---|---|
|
|\color{red}{\text{bourse pour champion}} : \color{blue}{\text{bourse pour finaliste}}| |
Établir l'ordre du rapport demandé. |
|
|\begin{align} \color{red}{3 \ 500} &: \color{blue}{5 \ 000 - 3 \ 500} \\ \Rightarrow\ \color{red}{3 \ 500} &: \color{blue}{1 \ 500} \end{align}| |
Déterminer les montants associés à chacune des parties. |
|
|\begin{align} \color{red}{35} &: \color{blue}{15} &(\div 100) \\ \color{red}{7} &: \color{blue}{3} &(\div 5) \end{align}| |
Réduire le rapport. |
|
La bourse est partagée dans un rapport |\color{red}{7}:\color{blue}{3}.| |
|
À voir aussi
Généralement noté |a / b|, le taux met en relation deux quantités de nature différente.
On fera référence au taux unitaire si |b=1.|
Voici la description des distances parcourues par un camionneur au cours de sa dernière semaine de travail :
|\color{red}{\text{Lundi} : 476\ \text{km en} \ 6{,}5 \ \text{h}}|
|\color{blue}{\text{Mardi} : 576\ \text{km en} \ 7{,}25 \ \text{h}}|
|\color{green}{\text{Mercredi} : 525\ \text{km en} \ 6{,}75 \ \text{h}}|
|\color{fuchsia}{\text{Jeudi} : 712\ \text{km en} \ 9 \ \text{h}}|
|\color{orange}{\text{Vendredi} : 632\ \text{km en} \ 7{,}75 \ \text{h}}|
À la lumière de ces informations, durant quelle journée le camionneur a-t-il maintenu la vitesse moyenne la plus élevée?
| CALCULS | JUSTIFICATIONS |
|---|---|
| |\color{red}{\text{Lundi} : 476\ \text{km en} \ 6{,}5 \ \text{h} = 476 \ \text{km} / 6{,}5 \ \text{h}}| |\color{blue}{\text{Mardi} : 576\ \text{km en} \ 7{,}25 \ \text{h} = 576 \ \text{km} / 7{,}25 \ \text{h}}| |\color{green}{\text{Mercredi} : 525\ \text{km en} \ 6{,}75 \ \text{h} = 525 \ \text{km} / 6{,}75 \ \text{h}}| |\color{fuchsia}{\text{Jeudi} : 712\ \text{km en} \ 9 \ \text{h} = 712 \ \text{km} / 9 \ \text{h}}| |\color{orange}{\text{Vendredi} : 632\ \text{km en} \ 7{,}75 \ \text{h} = 632 \ \text{km} / 7{,}75 \ \text{h}}| |
Transformer chacune des informations en taux. |
| |\color{red}{\text{Lundi} :476 \ \text{km} / 6{,}5 \ \text{h} \approx 73{,}23 \ \text{km/h}} \ (\div 6{,}5)| |\color{blue}{\text{Mardi} : 576 \ \text{km} / 7{,}25 \ \text{h} \approx 79{,}45 \ \text{km/h}}\ (\div 7{,}25)| |\color{green}{\text{Mercredi} : 525 \ \text{km} / 6{,}75 \ \text{h} \approx 77{,}78 \ \text{km/h}}\ (\div 6{,}75)| |\color{fuchsia}{\text{Jeudi} : 712 \ \text{km} / 9 \ \text{h} \approx 79{,}11 \ \text{km/h}}\ (\div 9)| |\color{orange}{\text{Vendredi} : 632 \ \text{km} / 7{,}75 \ \text{h} \approx 81{,}55 \ \text{km/h}}\ (\div 7{,}75)| |
Déterminer les taux unitaires. |
| Sa vitesse moyenne la plus élevée aura été durant la journée de |\color{orange}{\text{vendredi}}|. | |
À voir aussi
Pour qu'une situation soit proportionnelle, le graphique qui lui est associé doit :
-
passer par l'origine |(0,0),|
-
être représenté par une ligne droite.
Une fois qu'on s'est assuré que la situation répond à ces critères, on peut utiliser le produit croisé ou le coefficient multiplicatif pour résoudre le problème.
Afin de s'assurer de la justesse de sa soumission, une compagnie d'installation d'équipements de chauffage se base sur le graphique suivant afin d'estimer ses dépenses :
Ainsi, à combien devrait se chiffrer une soumission pour laquelle le temps de travail estimé est de |\color{red}{125 \ \text{heures}}|?
| CALCULS | JUSTIFICATIONS |
|---|---|
|
Déterminer si c'est une situation de proportionnalité. |
|
|\begin{align} \text{Heures}\ \quad &\text{Cout} \\ \displaystyle \frac{\color{green}{1{,}4}}{\color{red}{125}} =\ &\frac{\color{green}{100{,}8}}{\color{red}{?}} \end{align}| |
Construire la proportion. |
|
|\begin{align} \color{red}{?} &= \displaystyle \frac{\color{green}{100{,}8} \times \color{red}{125}}{\color{green}{1{,}4}} \\ &= \color{red}{9 \ 000\ $} \end{align}| |
Résoudre la proportion. |
|
La soumission devrait s'élever à |9 \ 000\ $.| |
|
À voir aussi
Pour qu'une situation soit inversement proportionnelle, il faut que le graphique qui lui est associé soit :
-
une ligne courbe décroissante,
-
une ligne qui ne touche pas l'axe des abscisses et des ordonnées.
Une fois qu'on s'est assuré que la situation répond à ces critères, on peut la résoudre selon |x y = k| où |k| est une constante.
Lors de la remise des lots des tirages hebdomadaires d'une loterie nationale, on sépare également le gros lot selon le nombre de gagnants. Voici une illustration de la dernière répartition :
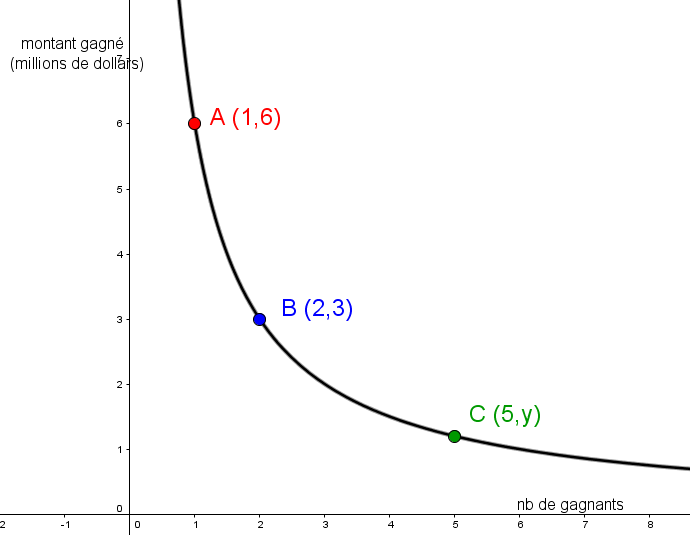
Selon ce contexte, détermine le montant gagné par chaque participant si on sait qu'il y a eu 5 gagnants?
| CALCULS | JUSTIFICATIONS |
|---|---|
|
Déterminer si c'est une situation de proportionnalité inverse. |
|
|\begin{align} k &= \color{blue}{x y} \\ &= \color{blue}{2\times 3} \\ &= 6 \end{align}| |
Trouver la valeur de la constante |k| selon |k = xy.| |
|
|\begin{align} k &= x y \\ 6 &= \color{green}{5} y \\ 1{,}2 &= y \end{align}| |
Remplacer |k| par |6| et |x| par |\color{green}{5}| pour finalement isoler |y.| |
|
Selon le contexte, chaque gagnant obtiendra la somme de |1{,}2| million de dollars. |
|
À voir aussi
Afin de bien saisir le rôle de chacune des composantes en algèbre, on leur a attribué des noms précis :
-
Inconnue : Valeur numérique recherchée.
-
Variable : Lettre utilisée pour identifier l'inconnue.
-
Coefficient : Facteur multiplicatif placé devant l'inconnue.
-
Termes : Parties d'une expression ou d'une équation qui sont séparées par des additions ou des soustractions.
-
Terme constant (constante) : Terme composé uniquement d'un nombre ou dans lequel ne figure aucune variable.
-
Termes semblables : Termes composés des mêmes variables et dont ces variables sont affectées des mêmes exposants.
-
Expression algébrique : Combinaison de plusieurs termes dont on ne connait pas le total (aucun signe =).
-
Degré : Dans un monôme, il correspond à la somme des exposants des variables. Dans un polynôme, il correspond au degré le plus élevé parmi les monômes qui le composent.
-
Équation algébrique : Combinaison de plusieurs termes dont on connait le résultat (avec un signe =).
En te référant à l'expression algébrique suivante : ||\color{blue}{-4x^3y} \color{red}{+3x^2} \color{fuchsia}{-\frac{3}{4} xy^4 } \color{green}{+ 9} \color{orange}{- 4xy^4}||identifie :
A) Un terme constant.
B) S'il s'agit d'une expression ou d'une équation.
C) Son degré.
D) Des termes semblables, s'il y a lieu.
E) Le coefficient du 2e terme.
| RÉPONSES | JUSTIFICATIONS |
|---|---|
|
A) |9| |
Puisque c'est le seul terme composé uniquement d'un nombre, sans variable. |
|
B) Expression algébrique |
Puisque le total de tous ces termes est inconnu (aucun signe d'égalité). |
|
C) |5| |
En faisant la somme des exposants des variables de chacun des termes, on obtient |5| comme plus grand total |(\color{orange}{-4xy^4} =- 4x^1y^4 \Rightarrow 1 + 4 = 5).| |
|
D) |\color{fuchsia}{-\frac{3}{4}xy^4}| et |\color{orange}{-4xy^4}| |
Ils possèdent les mêmes variables et celles-ci sont affectées des mêmes exposants. |
|
E) |3| |
|2^e| terme |= \color{red}{ \underline{+3}x^2} \Rightarrow \color{red}{\underline{3}}| est le coefficient. |
À voir aussi
Pour simplifier une expression algébrique, il suffit d'appliquer la priorité des opérations en gardant ceci en mémoire :
-
Multiplication et division : elles sont appliquées sur les coefficients, peu importe les termes.
-
Addition et soustraction : elles sont appliquées sur les coefficients des termes semblables.
-
Évaluer une expression algébrique : substituer les variables par les valeurs données.
Afin de gagner en efficience, une compagnie a modélisé ses revenus mensuels à l'aide de l'expression algébrique suivante : ||\displaystyle 2(4x^2-6) - \frac{1}{2}x^2 + (12x - 1) \div 4||
où |x = | nombre d'heures travaillées par tous les employés
Ainsi, quels seraient les revenus amassés pour un total de |325| heures travaillées en un mois?
| CALCULS | JUSTIFICATIONS |
|---|---|
|
||\begin{align} &\underline{2(4x^2-6)} - \frac{1}{2}x^2 + (12x - 1) \div 4 \\\\ =\ &8x^2-12-\frac{1}{2}x^2 +\underline{(12x-1)\div 4} \\\\ =\ &\color{blue}{8x^2}\color{red}{-12}\color{blue}{-\frac{1}{2}x^2} + 3x \color{red}{- \frac{1}{4}} \\\\ =\ &\color{blue}{\frac{15}{2}x^2}+3x \color{red}{-\frac{49}{4}} \end{align}|| |
Simplifier l'expression algébrique. |
|
||\begin{align} \text{Profit} &=\color{blue}{\frac{15}{2} (325)^2}+3 (325) \color{red}{-\frac{49}{4}} \\\\ &= \color{blue}{792 \ 187{,}5} + 975 \color{red}{-12{,}25} \\\\ &= 793 \ 150{,}25\ $ \end{align}|| |
Substituer |x| par |325| et calculer le résultat final. |
|
La compagnie peut espérer des revenus de |793 \ 150{,}25\ $.| |
|
À voir aussi
Généralement, on peut résoudre une situation à l'aide de l'algèbre en suivant ces étapes :
-
Identifier les variables et les inconnues.
-
Créer l'équation selon la mise en situation.
-
Simplifier l'équation obtenue.
-
Résoudre l'équation en isolant la variable.
-
Valider sa réponse à l'aide de l'équation de départ.
Pour l'activité d'échange de cadeaux de ta classe, tu dois acheter un peu de nourriture pour le festin de groupe, des assiettes en carton et un cadeau pour l'échange qui aura lieu après le repas.
En analysant le tout, tu t'aperçois que la nourriture t'a couté |12\ $| de plus que le triple du montant pour les assiettes et tu as dû débourser la moitié de la somme des assiettes et de la nourriture pour ton cadeau.
En sachant que tu as dépensé exactement |36\ $| au total, détermine le montant de chacun des trois achats.
| CALCULS | JUSTIFICATIONS |
|---|---|
|
|\begin{align} \color{orange}{x} &= \text{cout des assiettes } ($) \\ \color{fuchsia}{3x + 12} &= \text{cout de la nourriture} ($) \\ \color{blue}{\displaystyle \frac{(3x+12)+x}{2} } &= \text{cout du cadeau }($) \end{align}| |
Identifier les inconnues et les variables. |
|
|36 =\color{orange}{ x} +\color{fuchsia}{(3x+12)} + \color{blue}{\displaystyle \frac{(3x+12)+x}{2}}| |
Créer l'équation. |
|
|36 = x + 3x + 12 + \displaystyle \frac{4x+12}{2}| |
Simplifier l'équation. |
|
|\begin{align} 36 \color{red}{-18} &= 6x + 18 \color{red}{-18} \\ \displaystyle \frac{18}{ \color{red}{6}} &= \frac{6x}{\color{red}{6}} \\ \color{green}{3} &= \color{green}{x} \end{align}| |
Résoudre en isolant la variable. |
|
|\begin{align} 36 &= x +(3x+12) + \dfrac{(3x+12)+x}{2} \\ \Rightarrow\ 36 &\overset{?}{=} \color{green}{3} + (3\times \color{green}{3}+12) + \dfrac{(3\times \color{green}{3}+12)+\color{green}{3}}{2} \\ 36 &\overset{?}{=} 3 + 9 + 12 + \dfrac{24}{2} \\36 &= 36 \end{align}| |
Valider en substituant la valeur de |x| trouvée dans l'équation de départ. |
|
Ainsi, le cout pour les assiettes |= \color{orange}{x = 3\ $},| le cout pour la nourriture |=\color{fuchsia}{3x + 12 = 3 \times3 + 12 = 21\ $}| et le cout pour le cadeau |=\color{blue}{\displaystyle \frac{(3x+12)+x}{2} = \frac{(3 \times 3 + 12)+3}{2} = 12\ $}.| |
|
À voir aussi
Unités d'aire
Quelle est la mesure, en |\text{m}^2,| d'un triangle dont la base mesure |\color{blue}{ 820 \ \text{cm}}| et la hauteur est de | \color{red}{1{,}2 \ \text{dam}}|?
| CALCULS | JUSTIFICATIONS |
|---|---|
|
||\begin{align} \color{blue}{820 \ \text{cm}} &= (820 \div 100) \ \text{m} \\ &= \color{blue}{8{,}2 \ \text{m}} \\\\ \color{red}{1{,}2 \ \text{dam}} &= (1{,}2 \times 10) \ \text{m} \\ &= \color{red}{12 \ \text{m}} \end{align}|| |
Transformer les unités de départ en mètre puisqu'on veut le résultat en mètres carrés. |
|
||\begin{align} A_\text{triangle} &= \displaystyle \frac{\color{blue}{b} \times \color{red}{h}}{2} \\ &= \displaystyle \frac{\color{blue}{8{,}2} \times \color{red}{12}}{2} \\ &= 49{,}2 \ \text{m}^2 \end{align}|| |
Appliquer la formule d'aire d'un triangle. |
|
L'aire d'un tel triangle est de |49{,}2 \ \text{m}^2.| |
|
À voir aussi
Dans le but de définir les différentes figures planes et de trouver des mesures manquantes, on fait souvent référence à des types de segments particuliers :
-
|\color{blue}{\text{Diagonale}\ (\overline{BD})}| : segment qui relie deux sommets qui ne sont pas adjacents.
-
|\color{red}{\text{Médiane} \ (\overline{DF})}| : segment qui relie un sommet avec le milieu de son côté opposé.
-
|\color{green}{\text{Médiatrice}\ (\overline{FH})}| : segment qui est perpendiculaire à un autre segment et qui divise ce dernier en deux parties égales.
-
|\color{fuchsia}{\text{Bissectrice}\ (\overline{DE})}| : segment qui divise un angle en deux parties égales.
-
|\color{orange}{\text{Hauteur}\ (\overline{DG})}| : segment issue du sommet d'une figure ou d'un solide qui est perpendiculaire à sa base.
En te basant sur le dessin plus bas, associe chaque type de segment à un élément de l'illustration.
A) Identifie une médiane.
B) Identifie une médiatrice.
C) Identifie une hauteur.
D) Identifie une bissectrice.
| RÉPONSES | JUSTIFICATIONS |
|---|---|
|
A) Médiane : |\color{fuchsia}{\overline{AF}}| |
C'est le seul segment qui relie un sommet avec le milieu du côté qui lui est opposé. |
|
B) Médiatrice : |\color{red}{\overline{IJ}}| |
C'est le seul segment qui est perpendiculaire et au milieu d'un côté du polygone |(\overline{BC}).| |
|
C) Hauteur : |\overline{AE}| |
C'est le seul segment qui relie perpendiculairement un segment et le sommet qui est le plus éloigné. |
|
D) Bissectrice : |\color{green}{\overline{DM}}| |
C'est le seul segment qui divise un angle en deux parties égales. |
À voir aussi
Les polygones réguliers possèdent toutes les mêmes propriétés :
-
Tous les côtés ont la même mesure.
-
Tous les angles ont la même mesure.
-
La somme des angles intérieurs peut se calculer à l'aide de la formule : |(n-2) \times 180°| où |n| est le nombre de côtés.
-
Ils sont formés d'un ensemble de triangles isocèles, sauf l'hexagone, formé de triangles équilatéraux.
-
Ils possèdent tous un nom différent en fonction de leur nombre de côtés.
-
L'apothème correspond au segment reliant le centre du polygone avec le milieu d'un côté.
-
L'apothème est perpendiculaire au côté qu'il touche.
Vrai ou faux : un octogone régulier dont la mesure d'un côté est de |\color{red}{8 \ \text{cm}}| a un plus grand périmètre qu'un décagone régulier dont un côté mesure |\color{blue}{7 \ \text{cm}}.|
| CALCULS | JUSTIFICATIONS |
|---|---|
|
|\begin{align} P_\text{octogone} &= \color{red}{c} \times n \\ &= \color{red}{8} \times 8 \\ &= 64 \ \text{cm} \end{align}| |
Calculer le périmètre de l'octogone régulier. |
|
|\begin{align} P_\text{décagone} &= \color{blue}{c} \times n \\ &= \color{blue}{7} \times 10 \\ &= 70 \ \text{cm} \end{align}| |
Calculer le périmètre du décagone régulier. |
|
L'énoncé est faux puisque |70 > 64\ \Rightarrow\ P_\text{décagone} > P_\text{octogone}| |
|
À voir aussi
Pour bien distinguer les propriétés des différents segments de droite dans un cercle, on utilise les termes suivants :
-
|\color{orange}{\text{Corde} \ (\overline{CF})}| : segment qui relie deux points quelconques du cercle.
-
|\color{red}{\text{Diamètre}\ (\overline{DE})}| : segment qui relie deux points quelconques du cercle en passant par le centre.
-
|\color{green}{\text{Rayon} \ (\overline{AO})}| : généralement noté |r|, c'est un segment qui relie le centre du cercle à un point quelconque de celui-ci.
-
Circonférence du cercle |=| contour du cercle |= 2 \pi r.|
-
|\color{fuchsia}{\text{Arc de cercle} \ \overset{\huge\frown}{\small {AB}}}| : portion du cercle qui est interceptée par deux rayons. ||\displaystyle \frac{\color{fuchsia}{m \overset{\huge\frown}{\small {AB}}}}{\color{fuchsia}{m \ \angle AOB}} = \displaystyle \frac{\text{Circonférence}}{360^\circ}||
-
Aire du disque |=| surface recouverte par le disque |= \pi r^2.|
-
Aire d'un secteur : portion du disque qui est délimitée par deux rayons. ||\displaystyle \frac{\text{aire du secteur} AOB}{\text{aire du disque}}= \displaystyle \frac{\color{fuchsia}{m \ \angle AOB}}{360^\circ}||
Pour capturer le bétail, les cowboys utilisent un lasso qui est composé de deux parties : la corde et la boucle. Lorsque la boucle est défaite, un cowboy de profession enroule le lasso autour de lui-même huit fois avant de le déposer sur un crochet. Par ailleurs, la longueur nécessaire pour faire une boucle correspond à un arc de cercle intercepté par un angle au centre de |\color{red}{325^\circ}.|
Ainsi, quelle est la longueur de la corde, soit la partie du lasso sans la boucle?
| CALCULS | JUSTIFICATIONS |
|---|---|
|
||\begin{align} \dfrac{\color{fuchsia}{\text{m arc de cercle}}}{\text{m angle au centre}} &= \dfrac{\text{Circonférence}}{360^\circ} \\ \Rightarrow\ \dfrac{\color{fuchsia}{\text{m arc de cercle}}}{\color{red}{325^\circ}} &= \displaystyle \frac{2 \pi (\color{blue}{40}\div 2)}{360^\circ} \\\\ \Rightarrow\ \ \color{fuchsia}{\text{m arc de cercle}} &= \displaystyle \frac{\color{red}{325^\circ} \times 2 \pi (20)}{360^\circ} \\ &\approx \color{fuchsia}{113{,}45 \ \text{cm}} \end{align}|| |
Déterminer la mesure de l'arc de cercle. |
|
||\begin{align} \color{green}{\text{Longueur initiale}} &= 8 \times \text{Circonférence} \\ &= 8 \times 2 \pi (\color{blue}{40} \div 2) \\ &\approx \color{green}{1 \ 005{,}31 \ \text{cm}} \end{align}|| |
Déterminer la longueur initiale du lasso. |
|
||\begin{align} \text{Longueur finale} &= \color{green}{\text{Longueur initiale}} - \color{fuchsia}{\text{Boucle}} \\ &=\color{green}{1 \ 005{,}31} - \color{fuchsia}{113{,}45} \\ &= 891{,}86 \ \text{cm} \end{align}|| |
Déterminer la longueur finale du lasso. |
|
En enlevant la longueur de la boucle, le lasso a une longueur de |891{,}86 \ \text{cm}.| |
|
À voir aussi
Puisqu'il est question d'une figure décomposable, il faudra travailler avec l'aire de chacune de ses faces. Ainsi, les formules d'aire des figures planes seront à privilégier.
|
|A_\text{carré} = c^2| |
|A_\text{rectangle} = b\times h| |
|A_\text{losange} = \displaystyle \frac{D \times d}{2}| |
|
|A_\text{parallélogramme}=b \times h| |
|A_\text{trapèze} = \displaystyle \frac{(B+b)\times h}{2}| |
|A_\text{triangle} = \displaystyle \frac{b \times h}{2}| |
|
|A_\text{disque}=\pi r^2| |
|A_\text{polygone régulier}= \displaystyle \frac{c a n}{2}| |
|
Avec la saison hivernale qui s'en vient, un entrepreneur en machinerie lourde fait ses soumissions afin d'obtenir des contrats de déneigement. Afin d'être compétitif, il demande |3{,}50\ $ / \text{m}^2.|
En tenant compte des dimensions fournies plus haut, quel sera le montant de la soumission de ce contrat de déneigement?
| CALCULS | JUSTIFICATIONS |
|---|---|
|
Diviser la figure en plusieurs figures dont on connait les formules d'aire. |
|
|
|\begin{align} A_\text{trapèze} &= \dfrac{ (\color{fuchsia}{B}+\color{blue}{b}) \times h}{2} \\ &= \dfrac{ (\color{fuchsia}{12} + \color{blue}{8}) \times (\color{red}{15}-\color{green}{13})}{2} \\ &= \displaystyle \frac{ 20 \times 2}{2} \\ &= 20 \ \text{m}^2 \end{align}| |\begin{align} A_\text{rectangle} &= \color{fuchsia}{b} \times \color{green}{h} \\ &= \color{fuchsia}{12} \times \color{green}{13} \\ &= 156 \ \text{m}^2 \end{align}| |\begin{align} A_\text{demi -disque} &= \dfrac{\pi r^2}{2} \\ &= \dfrac{\pi (\color{green}{13} \div 2)^2}{2} \\ &\approx 66{,}37 \ \text{m}^2 \end{align}| |
Calculer l'aire de chacune des sections. |
|
|\begin{align} A_\text{totale} &= A_\text{trapèze} + A_\text{rectangle} + A_\text{demi-disque} \\ &= 20 + 156 + 66{,}37 \\ &= 242{,}37 \ \text{m}^2 \end{align}| |
Calculer l'aire totale du terrain. |
|
|\begin{align} \text{Montant final} &= 242{,}33 \times 3{,}50 \\ &= 848{,}16 \ $ \end{align}| |
Calculer le montant final de la soumission. |
|
Le montant de la soumission devra être de |848{,}16 \ $.| |
|
À voir aussi
Puisqu'il est question d'un solide décomposable, il sera préférable de travailler avec l'aire de chacune de ses faces plutôt que de travailler avec l'aire totale de chacun des solides qui le composent. En d'autres mots, les formules d'aire des figures planes seront à privilégier.
|
|A_\text{carré} = c^2| |
|A_\text{rectangle} = b\times h| |
|A_\text{losange} = \displaystyle \frac{D \times d}{2}| |
|
|A_\text{parallélogramme}=b \times h| |
|A_\text{trapèze} = \displaystyle \frac{(B+b)\times h}{2}| |
|A_\text{triangle} = \displaystyle \frac{b \times h}{2}| |
|
|A_\text{disque}=\pi r^2| |
|A_\text{polygone régulier}= \displaystyle \frac{c a n}{2}| |
|
Avec le temps des Fêtes qui s'en vient, tu décides de jouer un tour à tes parents en emballant complètement leur cadeau avec du ruban adhésif gris. Concrètement, il s'agit d'un prisme à base carrée surmonté d'un cylindre.
En considérant les mesures fournies dans le dessin plus haut, quelle quantité de ruban adhésif, en |\text{dm}^2,| devras-tu utiliser?
| CALCULS | JUSTIFICATIONS |
|---|---|
|
|\begin{align} \color{red}{A_\text{rectangles}} &= 4 \times (4,1 \times 2{,}4) \\ &= \color{red}{39{,}36 \ \text{dm}^2} \end{align}| |\begin{align} A_\text{dessous} &= 4{,}1^2 \\ &= 16{,}81 \ \text{dm}^2 \end{align}| |\begin{align} \color{orange}{A_\text{dessus}} &= A_\text{carré} - A_\text{disque} \\ &= 4{,}1^2 - \pi (4{,}1 \div 2)^2 \\ &\approx \color{orange}{3{,}61 \ \text{dm}^2} \end{align}| |\begin{align} \color{green}{A_\text{latérale du cylindre}} &= 2 \pi (4{,}1\div 2) \times (3{,}5-2{,}4) \\ &\approx \color{green}{14{,}16 \ \text{dm}^2} \end{align}| |\begin{align} \color{blue}{A_\text{disque}} &= \pi (4{,}1\div 2)^2 \\ &\approx \color{blue}{13{,}20 \ \text{dm}^2} \end{align}| |
Calculer l'aire de chacune des surfaces. |
|
|\begin{align} A_\text{totale} &= \color{red}{39{,}36} + 16{,}81 + \color{orange}{3{,}61} + \color{green}{14{,}16} + \color{blue}{13{,}20} \\ &= 87{,}14 \ \text{dm}^2 \end{align}| |
Faire le total de l'aire de chacune des sections. |
|
Tu devras utiliser au moins |87{,}14 \ \text{dm}^2| de ruban adhésif. |
|
À voir aussi
Les étapes à suivre pour trouver une mesure manquante sont les suivantes :
-
Identifier les mesures données.
-
Déterminer la formule à utiliser.
-
Remplacer les variables connues.
-
Isoler la variable recherchée.
Une fois arrivé dans un magasin d'antiquités, un collectionneur aperçoit ce coffre. S'il l'achète, il aura besoin de connaitre la hauteur totale de ce dernier puisqu'il doit être semblable à ceux qu'il possède déjà. Pour des fins de restauration, l'aire totale est connue.
Quelle est la hauteur de ce coffre?
| CALCULS | JUSTIFICATIONS |
|---|---|
|
Identifier les mesures données. |
|
|
|\begin{align}A_\text{totale} =\ &A_\text{base}+2 A_\text{faces gauche-droite}+2 A_\text{faces avant-arrière} \\ &+ \frac{1}{2}A_\text{L cylindre} + A_\text{disque} \\\\ \displaystyle 7{,}15 =\ &\color{red}{1{,}35}\times \color{fuchsia}{0{,}9} + 2 (\color{fuchsia}{0{,}9}\times \color{blue}{h}) + 2 (\color{red}{1{,}35}\times \color{blue}{h}) \\ &+ \frac{1}{2} (2 \pi \times \color{fuchsia}{0{,}45} \times \color{red}{1{,}35}) + \pi\times \color{fuchsia}{0{,}45}^2 \end{align}| |
Déterminer la formule à utiliser.
Remplacer les variables connues. |
|
|\begin{align} 7{,}15 &\approx 1{,}215 + 1{,}8\color{blue}{h} + 2{,}7\color{blue}{h} + 1{,}908+0{,}636 \\ 7{,}15 &\approx 3{,}759 + 4{,}5\color{blue}{h} \\ 3{,}391 &\approx 4{,}5\color{blue}{h} \\ \color{blue}{0{,}75} &\approx \color{blue}{h} \end{align}| |
Isoler la variable recherchée |(\color{blue}{h}).| |
|
La hauteur totale du coffre | \approx \color{blue}{h} + \color{fuchsia}{0{,}45} \approx \color{blue}{0{,}75}+\color{fuchsia}{0{,}45} \approx 1{,}2 \ \text{m}.| |
|
À voir aussi
Voici le nom des angles en fonction de leur mesure :
-
Un angle nul : angle qui mesure |0^\circ.|
-
Un angle aigu : angle dont la mesure est comprise entre |0^\circ| et |90^\circ.|
-
Un angle droit : souvent représenté à l'aide d'un carré noir, il s'agit d'un angle dont la mesure est exactement de |90^\circ.|
-
Un angle obtus : angle dont la mesure est comprise entre |90^\circ| et |180^\circ.|
-
Un angle plat : angle dont la mesure est exactement de |180^\circ.|
-
Un angle rentrant : angle dont la mesure est comprise entre |180^\circ| et |360^\circ.|
-
Un angle plein : angle qui mesure |360^\circ.|
Voici quelques définitions qui concernent des paires d'angles :
-
Les angles adjacents : une paire d'angles qui ont un sommet et un côté commun et qui sont situés de chaque côté de l'angle commun.
-
Les angles complémentaires : deux angles dont la somme de leurs mesures est de |90^\circ.|
-
Les angles supplémentaires : deux angles dont la somme de leurs mesures est de |180^\circ.|
Par ailleurs, lorsque deux droites sont coupées par une sécante, cela forme des paires d'angles remarquables. Si les droites sont parallèles, alors on retrouvera plusieurs angles congrus.
Soit |d_1 // d_2| et |d_3,| une sécante :
Les angles suivants sont congrus :
-
Les angles alternes-internes |(\color{redorange}{m\angle BEG} = \color{fuchsia}{m\angle CBE})| : angles qui sont de part et d'autres de la sécante, qui ne partagent pas le même sommet et qui sont à l'intérieur des droites parallèles.
-
Les angles alternes-externes |(\color{green}{m\angle ABF} = \color{orange}{m\angle DEH})| : angles qui sont de part et d'autres de la sécante, qui ne partagent pas le même sommet et qui sont à l'extérieur des droites parallèles.
-
Les angles correspondants |(\color{red}{m\angle ABC} = m\angle BED)| : angles qui sont du même côté de la sécante et qui ne partagent pas le même sommet. Par ailleurs, il y en a un qui est à l'intérieur des droites parallèles et l'autre, à l'extérieur.
-
Les angles opposés par le sommet |(\color{blue}{m\angle FBE} = \color{red}{m\angle ABC})| : angles qui partagent le même sommet et dont les côtés de l'un sont le prolongement des côtés de l'autre.
Finalement, pour déduire des mesures d'angles, il est parfois utile d'utiliser le fait que la somme des angles intérieurs d'un triangle est de |180^\circ.| Pour les autres polygones, on peut appliquer la formule suivante :
-
La somme des angle intérieurs d'un polygone |=(n-2)\times 180^\circ| où |n| est le nombre de côtés du polygone.
Quelle est |\color{red}{m\angle CBL}| dans le dessin suivant?
Voici une des nombreuses démarches possibles pour arriver à la solution :
| CALCULS | JUSTIFICATIONS |
|---|---|
|
|m\angle GJC = m\angle QJP=43^\circ| |
Ce sont des angles opposés par le sommet. |
|
|m\angle BHG = m\angle MHG=90^\circ| |
Ce sont des angles adjacents supplémentaires : |\begin{align} m\angle BHG &= 180^\circ - m\angle GHM \\ &= 180^\circ - 90^\circ \\ &= 90^\circ \end{align}| |
|
|m\angle JGC = m\angle BHG = 90^\circ| |
Deux droites parallèles |(IK // ML)| coupées par une sécante |(PN)| forment des angles correspondants isométriques. |
|
|m\angle JCG = 47^\circ| |
Dans tout triangle, la somme des angles intérieurs est de |180^\circ.| Ainsi, dans le triangle |JCG,| on a : |\begin{align} 180^\circ &= m\angle JGC + m\angle GJC + m\angle JCG \\ 180^\circ &= 90^\circ + 43^\circ + m\angle JCG \\47^\circ &= m\angle JCG \end{align}| |
|
|m\angle GCB = 133^\circ| |
Il est supplémentaire à |\angle JCG:| |\begin{align} 180^\circ &= m\angle JCG + m\angle GCB \\ 180^\circ &= 47^\circ + m\angle GCB \\133^\circ &= m\angle GCB \end{align}| |
|
|\begin{align} \color{red}{m \angle CBL} =m\angle GCB = \color{red}{133^\circ} \end{align}| |
Deux droites parallèles |(IK // ML)| coupées par une sécante |(QB)| forment des angles alternes-internes isométriques. |
À voir aussi
Notée |t_{(x,y)}|, la translation est une isométrie puisque les mesures des angles et des côtés homologues sont identiques.
La translation est généralement définie par une flèche de translation.
À l'aide de tes instruments de géométrie, effectue la translation suivante :
| CALCULS | JUSTIFICATIONS |
|---|---|
|
Tracer des droites parallèles à la flèche de translation pour chacun des sommets. |
|
|
Mesurer la flèche de translation.
|
|
|
Utiliser cette mesure pour déterminer l'emplacement de chacun des sommets images. |
|
|
Relier les sommets images (mêmes lettres mais accompagnées du symbole ' ) dans le même ordre que les sommets de la figure initiale. |
À voir aussi
Notée |r_{(O,\text{degré})}|, la rotation est une isométrie puisque les mesures des angles et des côtés homologues sont identiques.
La rotation est définie par un angle de rotation.
À l'aide de tes instruments de géométrie, effectue la rotation demandée.
| CALCULS | JUSTIFICATIONS |
|---|---|
|
À partir du centre de rotation, tracer un cercle pour chacun des sommets à l'aide d'un compas. |
|
|
Pour chacun des cercles, mesurer l'ouverture correspondant à l'arc de cercle de chacun des sommets. |
|
|
Transposer cette mesure à partir du sommet. |
|
|
Répéter les deux étapes précédentes pour chacun des sommets. |
|
|
Relier les sommets de la figure image dans le même ordre que dans la figure initiale. |
À voir aussi
Notée |s_{\text{axe}}|, la réflexion (symétrie) est une isométrie puisque les mesures des angles et des côtés homologues sont identiques.
La réflexion est définie par un axe de symétrie.
À l'aide de tes instruments de géométrie, effectue la symétrie suivante :
| CALCULS | JUSTIFICATIONS |
|---|---|
|
Tracer des droites perpendiculaires à l'axe de symétrie pour chacun des sommets. |
|
|
Mesurer la distance entre l'axe de symétrie et un sommet. |
|
|
Reporter cette mesure sur la même droite, mais de l'autre côté de l'axe de symétrie. |
|
|
Répéter les deux étapes précédentes pour chacun des sommets. |
|
|
Relier les sommets images dans le même ordre que dans la figure initiale. |
À voir aussi
Notée |h_{(O,k)}|, l'homothétie établit une similitude entre deux figures puisque les angles homologues sont congrus et les côtés homologues sont proportionnels.
À l'aide de tes instruments de géométrie, effectue l'homothétie |h_{(O; 1,5)}|.
| CALCULS | JUSTIFICATIONS |
|---|---|
|
Tracer une droite reliant le centre d'homothétie |O| avec chacun des sommets. |
|
|
Mesurer la distance entre le centre d'homothétie |O| et chacun des sommets. |
|
|
|\begin{align} \text{m}\overline{OA'}&= \color{blue}{m\overline{OA}}\cdot\color{red}{k} \\ \Rightarrow\ \text{m} \overline {OA'} &= \color{blue}{6} \times \color{red}{1{,}5} \\ \Rightarrow\ \text{m} \overline{OA'} &= 9\ \text{cm} \\\\ \text{m}\overline{OB'} &= 9{,}3 \ \text{cm} \\ \text{m}\overline{OC'} &= 4{,}5 \ \text{cm} \end{align}| |
Appliquer le rapport d'homothétie à chacune des distances mesurées. |
|
Identifier le sommet image en rapportant la distance calculée à partir du centre d'homothétie |O|. |
|
|
Relier chacun des sommets images dans le même ordre que sur la figure initiale. |
À voir aussi
Peu importe le plan cartésien avec lequel on travaille, il possède toujours les mêmes caractéristiques :
-
Les quadrants : ils représentent chacune des quatre divisions du plan cartésien.
-
L'axe des abscisses : axe horizontal qui est associé à la variable indépendante |(x).|
-
L'axe des ordonnées : axe vertical qui est associé à la variable dépendante |(y).|
-
L'origine : point de rencontre des deux axes dont la coordonnée est |(0,0).|
-
Les coordonnées |(x,y)| : tout point dans le plan cartésien possède une coordonnée donnée en fonction de sa valeur sur l'axe des |x| et des |y.|
-
Les axes : chacun des axes est représenté par une droite graduée.
Dans un plan cartésien, place chacun des points suivants : ||A(2,3),\ B(-3,2),\ C(-2,-3),\ D(4,-2)||
À voir aussi
Pour bien comprendre les probabilités, il est important de bien différencier les différents événements :
-
Impossible : dont la probabilité est égale à 0 (0%).
-
Certain : dont la probabilité est 1 (100%).
-
Probable : dont la probabilité est entre 0 et 1 (entre 0% et 100%).
-
Élémentaire : qui contient un seul élément.
-
Compatibles/incompatibles : dont l'intersection n'est pas vide / dont l'intersection est vide.
-
Dépendants/indépendants : quand le résultat du 2e tirage est influencé par le 1er tirage / quand le résultat du 2e tirage n'est pas influencé par le 1er tirage.
En fonction des différentes situations, détermine les qualificatifs qui sont les plus appropriés pour chacune d'elles.
1) A : Tirer un as d'un jeu de cartes de 52 cartes.
B : Tirer un roi d'un autre jeu de 52 cartes.
2) Obtenir huit en lançant un dé à six faces.
3) Piger deux boules de façon consécutive et sans remise dans une urne qui en contient 30.
| CALCULS | JUSTIFICATIONS |
|---|---|
|
1) Événements incompatibles et indépendants. |
Incompatibles : Ces deux événements n'ont aucun élément en commun. Indépendants : Puisque les cartes sont tirées dans deux paquets différents, le 1er tirage n'a pas d'influence sur le 2e. |
|
2) Événement impossible. |
Impossible : Puisque les faces du dé sont numérotées de 1 à 6, il est impossible d'obtenir huit. |
|
3) Événements incompatibles et dépendants. |
Incompatibles : Il est impossible de piger deux fois la même boule. Dépendants : Puisque la 1re boule n'est pas remise dans l'urne avant qu'on en retire la 2e, le résultat du 2e tirage sera influencé par le 1er. |
À voir aussi
Tout comme dans plusieurs domaines, la théorie et la pratique donnent souvent deux résultats différents :
-
Probabilité fréquentielle : Probabilité qui est obtenue à la suite de la réalisation d'une expérience.
-
Probabilité théorique : Probabilité qui est obtenue à la suite de l'analyse théorique des résultats possibles.
En prenant connaissance des situations suivantes, identifie s'il s'agit d'une probabilité fréquentielle ou théorique.
A) Pour déterminer la probabilité d'obtenir pile ou face lorsqu'on lance une pièce de monnaie, Julien en lance une à 50 reprises et note les résultats chaque fois. Au final, il obient |P(\text{pile}) = \displaystyle \frac{23}{50}| et |P(\text{face})=\displaystyle \frac{27}{50}|.
B) Puisqu'un dé régulier possède six faces identiques, on peut déterminer que |P(1) = P(2) = P(3) = P(4) = P(5) = P(6) = \displaystyle \frac{1}{6}.|
| CALCULS | JUSTIFICATIONS |
|---|---|
|
A) Fréquentielle |
Puisque la probabilité est construite à la suite de la réalisation d'une expérience, c'est une probabilité fréquentielle. |
|
B) Théorique |
Puisque la probabilité est déterminée selon l'analyse de la situation, sans expérimentation, il s'agit d'une probabilité théorique. |
À voir aussi
||\mathbb{P} = \displaystyle \frac{\text{Nbre de résultats recherchés}}{\text{Nbre de résultats possibles}}||
Par ailleurs, le dénombrement des résultats possibles sera influencé si le tirage est fait avec ou sans remise.
Pour gagner le grand prix à une fête de quartier, les concurrents doivent piger deux boules noires de façon consécutive. Pour ce faire, ils ont le choix entre deux modalités.
A) Piger, sans remise, dans une urne qui contient 10 boules : cinq sont rouges, trois sont vertes et deux sont noires.
B) Piger, avec remise, dans une urne qui contient 15 boules : sept sont rouges, cinq sont vertes et trois sont noires.
Afin de maximiser ses chances, quelle modalité devraient choisir les concurrents?
| CALCULS | JUSTIFICATIONS |
|---|---|
|
A) ||\begin{align} P(\text{noire suivie d'une noire}) &= \dfrac{2}{10}\times \dfrac{1}{9} \\ &= \dfrac{2}{90} \\ &= \dfrac{1}{45} \\ &\approx 2{,}2\ \% \end{align}|| |
Calculer la probabilité en considérant que la 1re boule n'est pas remise dans l'urne pour le 2e tirage. |
|
B) ||\begin{align} P(\text{noire suivie d'une noire}) &= \dfrac{3}{15} \times \dfrac{3}{15} \\ &= \dfrac{9}{225} \\ &= \dfrac{1}{25} \\ &= 4\ \% \end{align}|| |
Calculer la probabilité en considérant que la 1re boule est remise dans l'urne pour le 2e tirage. |
|
La modalité B) est à privilégier puisque la probabilité de gagner est plus élevée |\big(P(A) = 4\ \% > P(B) \approx 2{,}2\ \%\big).| |
|
À voir aussi
Voici deux méthodes d'échantillonnage qui sont fréquemment utilisées :
-
Aléatoire : les éléments sont choisis au hasard, sans méthodologie précise.
-
Systématique : les éléments sont choisis en respectant une fréquence précise.
Pour chacune des situations, identifie laquelle des méthodes est la plus appropriée.
1) Dans une usine, on contrôle la qualité en vérifiant un produit à chaque tranche de 100 sortant de la chaine de production.
2) Pour essayer de prédire les résultats de la prochaine élection, on effectue un sondage en interrogeant les gens à la sortie d'un centre commercial.
| CALCULS | JUSTIFICATIONS |
|---|---|
|
1) Systématique |
Le contrôle de qualité s'effectue sur une fréquence régulière (1 à toutes les tranches de 100). |
|
2) Aléatoire |
Les gens interrogés sont choisis au hasard, c'est-à-dire sans tenir compte d'une caractéristique ou d'une fréquence précise. |
À voir aussi
Pour s'assurer de la crédibilité d'un sondage, il y a certains pièges qu'il faut éviter durant la création, la passation et l'analyse des données de celui-ci. Entre autres, les sources de biais suivantes sont souvent évoquées :
-
La taille de l'échantillon : s'assurer d'interroger assez de gens afin que les résultats soient représentatifs de la population.
-
La formulation des questions : s'assurer que les questions ne suggèrent aucune prise de position.
Parmi les situations suivantes, indique si la question est biaisée. Dans l'affirmative, identifie la source de biais.
A) Pour savoir ce que les gens pensent de l'agrandissement de l'hôtel de ville, le maire envoie un sondage, par la poste, à 1 000 des 5 000 résidents.
B) La question suivante est posée : « N'êtes-vous pas en accord avec le fait qu'une compagnie ne déménage pas son siège social pour éviter de perdre certains avantages fiscaux? »
| CALCULS | JUSTIFICATIONS |
|---|---|
|
A) Aucun biais |
Obtenir l'opinion de 1 000 personnes est très satisfaisant en terme de crédibilité. |
|
B) Biaisée : formulation de la question |
Il y a trop de négation dans la question. |
À voir aussi
De façon générale, on peut définir le type de caractère étudié à l'aide des qualificatifs suivants :
-
Qualitatif : lorsque la réponse est un mot ou une expression.
-
Quantitatif discret : lorsque la réponse est une valeur numérique faisant partie de l'ensemble des entiers |(\mathbb{Z}).|
-
Quantitatif continu : lorsque la réponse donnée est une valeur numérique faisant partie de l'ensemble des réels |(\mathbb{R}).|
Parmi les situations suivantes, identifie le caractère étudié ainsi que le type qui leur est associé.
A) On interroge les gens sur leur animal de compagnie préféré.
B) On interroge les gens sur le nombre d'animaux de compagnie qu'ils ont à leur domicile.
| CALCULS | JUSTIFICATIONS |
|---|---|
|
A) Caractère étudié : L'animal de compagnie Type : Qualitatif |
La réponse à cette question sera forcément un mot, soit l'espèce de l'animal de compagnie (chien, chat, oiseau, etc.). |
|
B) Caractère étudié : Le nombre d'animaux Type : Quantitatif discret |
La réponse à cette question sera forcément un nombre entier. |
À voir aussi
Une fois que les données ont été amassées, il faut les analyser afin d'en tirer des conclusions satisfaisantes. Pour ce faire, on utilise quelques valeurs numériques :
-
Moyenne |= \displaystyle \frac{\text{Somme des données}}{\text{Nombre total de données}}|
-
Étendue |= \text{Valeur maximale} - \text{Valeur minimale}|
-
Minimum | = \text{Plus petite valeur de la distribution}|
-
Maximum | = \text{Plus grande valeur de la distribution}|
Afin d'avoir une idée de la grandeur des vêtements sportifs qu'une école veut fournir aux membres des différentes équipes, elle demande à |\color{blue}{20}| élèves de donner leurs mensurations. Voici les résultats obtenus concernant la taille (en cm) de chacun :
|\color{green}{120,}| |\color{red}{124,}| |\color{red}{124,}| |\color{red}{ 125,}| |\color{red}{127,}| |\color{red}{128,}| |\color{red}{129,}| |\color{red}{130,}| |\color{red}{131,}| |\color{red}{134,}| |\color{red}{134,}| |\color{red}{134,}| |\color{red}{141,}| |\color{red}{142,}| |\color{red}{142,}| |\color{red}{143,}| |\color{red}{145,}| |\color{red}{147,}| |\color{red}{148,}| |\color{fuchsia}{149}|
À l'aide de cette distribution, détermine la valeur de la moyenne et de l'étendue.
| CALCULS | JUSTIFICATIONS |
|---|---|
|
||\begin{align} \text{Moyenne} &= \dfrac{\color{green}{120}\color{red}{+124+\dots+148}\color{fuchsia}{+149}}{\color{blue}{20}} \\ &= 134{,}85 \ \text{cm} \end{align}|| |
Appliquer la formule. |
|
||\begin{align} \text{Étendue} &= \color{fuchsia}{\text{max}} - \color{green}{\text{min}} \\ &= \color{fuchsia}{149}-\color{green}{120} \\&= 29\ \text{cm} \end{align}|| |
Identifier la valeur maximale |(149)| et minimale |(120)| pour ensuite appliquer la formule. |
|
La moyenne des tailles est de |134{,}85 \ \text{cm},| alors que la valeur de l'étendue est de |29\ \text{cm}.| |
|
À voir aussi
Afin de n'oublier aucun élément dans la création d'un tel diagramme, on peut suivre les étapes suivantes :
-
Construire un tableau de distribution.
-
Identifier les axes et le titre du graphique.
-
S'assurer d'une bonne graduation et d'un bon espace pour écrire les différentes modalités / valeurs du sondage.
-
Associer la longueur des bandes aux effectifs de chacune des modalités / valeurs.
À la sortie d'un centre d'achats, on s'informe sur le nombre de cadeaux que chaque personne pense offrir aux membres de leur famille immédiate. Voici les différentes réponses obtenues :
|3,| |4,| |2,| |6,| |5,| |3,| |5,| |6,| |1,| |4,| |1,| |5,| |4,| |6,| |8,| |5,| |6,| |8,| |4,| |5,| |3,| |6,| |2,| |4,| |5,| |2,| |6,| |5,| |3,| |2|
Afin d'avoir une idée plus juste des intentions des gens, regroupe ces données dans un diagramme à bandes.
| CALCULS | JUSTIFICATIONS |
|---|---|
|
1) Construire un tableau de distribution. |
|
|
2) Identifier le titre et les axes du graphique. |
|
|
3) Graduer les deux axes de façon appropriée. |
|
|
4) Dessiner les bandes horizontales ou verticales (au choix). |
À voir aussi
Afin de n'oublier aucun élément dans la création d'un tel diagramme, on peut suivre les étapes suivantes :
1) Construire un tableau de distribution avec les mesures d'angles au centre des secteurs.
| Modalités ou valeurs | Effectifs | Fréquence (%) | Angle au centre du secteur (°) |
|---|---|---|---|
|
Selon les choix de réponses offerts |
Dénombrement de chacune des modalités / valeurs |
|\displaystyle \frac{\text{Effectif analysé}}{\text{Effectif total}} \times 100| |
|\displaystyle \frac{\text{Fréquence}}{100 \%} = \frac{\text{m d'angle}}{360^\circ}| |
2) Dessiner chacun des secteurs en respectant leur angle au centre.
3) Ajouter une légende et un titre.
4) S'assurer que les pourcentages soient écrits sur chacun des secteurs.
Pour avoir une représentation globale de l'investissement des revenus d'une compagnie, le directeur général demande de synthétiser les informations suivantes dans un diagramme circulaire : ||\begin{align} \color{blue}{\text{Salaire}} &= \color{blue}{1 \ 190 \ 000\ $} \\ \color{orangered}{\text{Électricité}} &= \color{orangered}{420 \ 000\ $} \\ \color{gray}{\text{Chauffage}} &= \color{gray}{315 \ 000\ $} \\ \color{orange}{\text{Publicité}} &= \color{orange}{700 \ 000\ $} \\ \color{darkblue}{\text{Placements}} &= \color{darkblue}{245 \ 000\ $} \\ \color{green}{\text{Rénovations}} &= \color{green}{630 \ 000\ $} \end{align}||
À toi de jouer!
| CALCULS | JUSTIFICATIONS |
|---|---|
|
1) Construire le tableau de distribution. ||\begin{align} \% = \displaystyle \frac{\text{Montant} \times 100}{3\ 500\ 000} \\ \text{Angle} = \displaystyle \frac{\text{Montant}\times 360}{3\ 500\ 000} \end{align}|| |
|
 |
2) Dessiner les secteurs. |
 |
3) Ajouter une légende et un titre. |
 |
4) Ajouter les pourcentages sur chacun des secteurs. |