This is a preparation guide for the end-of-year exams containing all the concepts covered in the first cycle of secondary school. To explain it all, each concept will be followed by an example and a link to a concept sheet in our virtual library.
To compare numbers, it is better to use only one type of notation. Since the set of |\mathbb{Q}| contains the most elements with values that are easily illustrated, fractional notation |\left( \dfrac{a}{b} \right)| with |b \neq 0| will be used.
Place the following numbers in ascending order:
|4\dfrac{1}{3}\,| |\color{blue}{\dfrac{8}{3}}\,| |\color{red}{ -0{.}625}\,| |\color{green}{-80\ \%}\,| |\color{fuchsia}{\left( \dfrac{-1}{2} \right) ^2}\,| |\color{orange}{\sqrt9}|
|
CALCULATIONS |
JUSTIFICATIONS |
|---|---|
|
|\displaystyle4\frac{1}{3} = \frac{4 \times 3+ 1}{3} = \frac{13}{3}| |\color{blue}{\displaystyle\frac{8}{3}}| |\color{red}{\displaystyle-0.625 = \frac{-625}{1000} = \frac{-5}{8}}| |\color{green}{\displaystyle-80\%=\frac{-80}{100} = \frac{-4}{5}}| |\color{fuchsia}{\displaystyle\left( \frac{-1}{2} \right)^2 = \frac{-1}{2} \times \frac{-1}{2} = \frac{1}{4}}| |\displaystyle\color{orange}{\sqrt9 = 3}| |
Use simplified fractional notation to represent each of the quantities. |
|
|\displaystyle\frac{13}{3} = \frac{1040}{240}| |\color{blue}{\displaystyle\frac{8}{3}=\frac{640}{240}}| |\color{red}{\displaystyle\frac{-5}{8}=\frac{-150}{240}}| |\color{green}{\displaystyle\frac{-4}{5}=\frac{-192}{240}}| |\color{fuchsia}{\displaystyle\frac{1}{4}=\frac{60}{240}}| |\color{orange}{\displaystyle3=\frac{3}{1} = \frac{720}{240}}| |
Write all the numbers using a common denominator. |
|
Since the denominators are all equal, the numbers can be ordered according to their numerator, as follows: |\displaystyle \color{white}{=}\color{green}{\frac{-192}{240}} < \color{red}{\frac{-150}{240}} < \color{fuchsia}{\frac{60}{240}} < \color{blue}{\frac{640}{240}} < \color{orange}{\frac{720}{240}} < \frac{1040}{240}| |
|
See also
In word problems, it is important to fully understand the context in order to choose the best approach. Thus, it is useful to follow these steps:
-
Create the chain of operations by highlighting keywords
-
Solve by following the order of operations
To make sure he's prepared for his exam on Friday, Simon wants to know how many minutes he's studied. On Monday, he studied half the time that he studied Tuesday. On Tuesday, he had his nose in his books from 6:30 p.m. to 7:20 p.m. On Wednesday, he spent 20 minutes less than the sum of the previous two days reading his notes. On his last day, he spent three times more than Monday's amount of time reviewing his work.
In total, how many minutes did Simon spend studying for his exam?
|
CALCULATIONS |
JUSTIFICATIONS |
|---|---|
|
Total |=| Monday + Tuesday + Wednesday + Thursday |
Write the chain of operations that will be used to solve the problem |
|
|\color{white}{\text{Total}}=\color{blue}{\displaystyle \left( \frac{50}{2}\right)} + \color{red}{50} + \color{orange}{\left(\left(50 + \displaystyle \frac{50}{2}\right) - 20\right)} + \color{fuchsia}{3 \times \displaystyle \left( \frac{50}{2}\right)}| |
Replace each day with its respective value. |
|
|\color{white}{\text{Total}}=\color{blue}{25} + \color{red}{50} + \color{orange}{\left(\left(50 + \displaystyle \frac{50}{2}\right) - 20\right)} + \color{fuchsia}{3 \times \displaystyle \left(\frac{50}{2}\right)}| |
Solve the problem by following the order of operations. |
|
Simon spent |205| minutes preparing for his evaluation. |
|
See also
|
A number is divisible by... |
if... |
|---|---|
|
2 |
the ones digit is even. |
|
3 |
the sum of all digits in the number is divisible by 3. |
|
4 |
the number formed by its last two digits is divisible by 4, or if the number ends with at least two zeros. |
|
5 |
the ones digit is 0 or 5. |
|
6 |
the number is divisible by both 2 and 3. |
|
8 |
the number formed by its last three digits is divisible by 8, or when the number is divisible by 4 and 2. |
|
9 |
the sum of its digits is divisible by 9. |
|
10 |
the ones digit is 0. |
|
12 |
the number is divisible by both 3 and 4. |
|
25 |
the number ends with 00, 25, 50, or 75. |
Judith and her son Justin collected an impressive amount of candy from trick-or-treating in the neighbourhood on Halloween night. After a week and a few tummy aches, they want to give away what’s left. With Justin's birthday party just around the corner, Judith has come up with the great idea to share the rest of the |264| candies equally with each of Justin's friends who attend the party.
If Judith lets Justin invite |9| friends, will she be able to carry out her plan? If not, suggest a reasonable number of guests that would enable her to share the candy equally with everyone.
|
CALCULATIONS |
JUSTIFICATIONS |
|---|---|
|
|264 \Rightarrow 2 + 6 + 4 = 12| |
Determine if |264| is divisible by |9.| |
|
|264 \Rightarrow 64 \div 4 = 16| |
Find a divisor of |264| that is close to |9.| |
|
Judith should let Justin invite |8| of his friends instead. |
|
See also
The concept of a percentage is an example of a proportional situation. To properly build the proportion to find the desired quantities, follow these steps:
-
Identify the quantity given and associate a percentage with it.
-
Identify the quantity sought and associate a percentage with it.
-
Construct the proportion according to the following model: ||\displaystyle \frac{\color{red}{\text{Quantity given}}}{\color{blue}{\text{Quantity you’re looking for}}} = \frac{\color{red}{\text{Its percentage}}}{\color{blue}{\text{Its percentage}}}||
-
Solve the proportional situation.
To take advantage of the end-of-season sale in a sports store, Mrs. Caron bought some bicycle accessories. With a |\color{red}{45\ \%}| discount, she got what she wanted for only |\color{red}{$14{.}85}|, taxes included.
What was the price (taxes included) before the discount?
|
CALCULATIONS |
JUSTIFICATIONS |
|---|---|
|
|\begin{align} \color{red}{\text{Quantity given}} &= \color{red}{\text{Its percentage}} \\ \color{red}{$14{.}85 \ } &= \color{red}{100\ \% - 45\ \%} \\ \color{red}{$14{.}85\ } &= \color{red}{55\ \%} \end{align}| |
Identify the quantity given and associate a percentage with it. |
|
|\begin{align} \color{blue}{\text{Quantity you are looking for}} &= \color{blue}{\text{Its percentage}}\\ \color{blue}{\text{Price before discount}} &= \color{blue}{100\ \%} \end{align}| |
Identify the quantity you are looking for and its percentage. |
|
|\Rightarrow \displaystyle \frac{\color{red}{$14{.}85 \ }}{\color{blue}{\text{Price before discount}}} = \frac{\color{red}{55\ \%}}{\color{blue}{100\ \%}}| |
Build the proportion. |
|
|\begin{align} \color{blue}{\text{Price before discount}} &= \displaystyle \frac{\color{blue}{100\ \%}\times \color{red}{$14{.}85\ \ }}{\color{red}{55\ \%}} \\ \color{blue}{\text{Price before discount}} &= \color{blue}{$27\ } \end{align}| |
Solve the proportion. |
|
Without the discount, she would have paid |$27| for her purchase. |
|
See also
We express a ratio using two superimposed points or a fraction.
|a : b| is the part-to-part ratio.
|\displaystyle \frac{a}{a+b}| is the part-to-whole ratio,
where |a| and |b| are parts of the same whole and generally prime (simplified ratio)
By definition, parts |a| and |b| of a ratio |a:b| are like units, thus, entering the units associated with each part is unnecessary.
After a professional sports competition, a bursary of |$5\ 000| was shared between the winning team and the other finalists. When the cheques were given, the winning team won |\color{red}{$3\ 500}|. The rest was given to the finalists.
What is the ratio associated with the amount given to the winners versus the finalists?
|
CALCULATIONS |
JUSTIFICATIONS |
|---|---|
|
|\color{red}{\text{Winner’s bursary}} : \color{blue}{\text{Finalist’s bursary}}| |
Establish the order for the ratio. |
|
|\begin{align} \color{red}{3 \ 500} &: \color{blue}{5 \ 000 - 3 \ 500} \\ \Rightarrow\ \color{red}{3 \ 500} &: \color{blue}{1 \ 500} \end{align}| |
Determine the amount of each part. |
|
|\begin{align} \color{red}{35} &: \color{blue}{15} &(\div 100) \\ \color{red}{7} &: \color{blue}{3} &(\div 5) \end{align}| |
Simplify the ratio. |
|
The bursary is shared using a ratio of |\color{red}{7}:\color{blue}{3}.| |
|
See also
Generally denoted |a / b|, the rate creates a relationship between two unlike quantities or measurements.
We call this a unit rate if |b=1.|
The following describes the distance traveled by a truck driver during his most recent week of work:
|\color{red}{\text{Monday}: 476\ \text{km in} \ 6{.}5 \ \text{hrs}}|
|\color{blue}{\text{Tuesday}: 576\ \text{km in} \ 7{.}25 \ \text{hrs}}|
|\color{green}{\text{Wednesday}: 525\ \text{km in} \ 6{.}75 \ \text{hrs}}|
|\color{fuchsia}{\text{Thursday}: 712\ \text{km in} \ 9 \ \text{hrs}}|
|\color{orange}{\text{Friday}: 632\ \text{km in} \ 7{.}75 \ \text{hrs}}|
Based on the information given, on what day did the truck driver maintain the highest average speed?
|
CALCULATIONS |
JUSTIFICATIONS |
|---|---|
|
|\color{red}{\text{Monday}: 476\ \text{km in} \ 6{.}5 \ \text{hrs} = 476 \ \text{km} / 6{.}5 \ \text{hrs}}| |
Convert each piece of information into a rate. |
|
|\color{red}{\text{Monday}:476 \ \text{km} / 6{.}5 \ \text{hrs} \approx 73{.}23 \ \text{km/h}} \ (\div 6{.}5)| |
Determine the unit rates. |
|
His highest average speed was on |\color{orange}{\text{Friday}}| . |
|
See also
For a situation to be proportional, the associated graph needs to:
-
Pass through the origin |(0,0).|
-
Be represented by a straight line.
Once the situation meets these criteria, use cross multiplication or the multiplicative coefficient to solve the problem.
To ensure the accuracy of their estimate, a heating equipment installation company uses the graph below to estimate expenses:

How much should the estimate be if the approximate amount of work is |\color{red}{125 \ \text{hours}}|?
|
CALCULATIONS |
JUSTIFICATIONS |
|---|---|
|
Determine if this is a proportional situation. |
|
|\begin{align} \text{Hours}\ \quad &\text{Cost} \\ \displaystyle \frac{\color{green}{1{.}4}}{\color{red}{125}} =\ &\frac{\color{green}{100{.}8}}{\color{red}{?}} \end{align}| |
Build the proportion. |
|
|\begin{align} \color{red}{?} &= \displaystyle \frac{\color{green}{100{.}8} \times \color{red}{125}}{\color{green}{1{.}4}} \\ &= \color{red}{9 \ 000\ $} \end{align}| |
Solve the proportion. |
|
The company's estimate should amount to |$9 \ 000.| |
|
See also
For a situation to be inversely proportional the associated graph must have:
-
A decreasing curved line.
-
A line that does not touch the x-axis and y-axis.
Once the situation meets these criteria, it can be solved according to |x y = k|, where |k| is a constant.
When awarding prizes for the weekly draw of a national lottery, the jackpot is divided according to the number of winners. Here is an illustration of the last jackpot’s distribution:
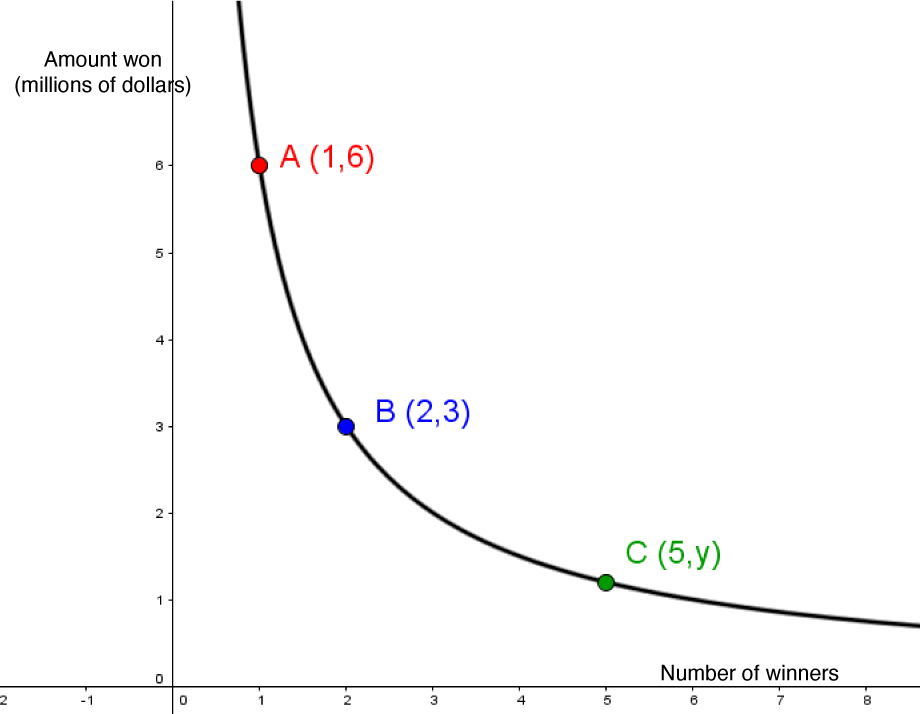
According to this situation, what amount would each participant win if there were 5 winners?
|
CALCULATIONS |
JUSTIFICATIONS |
|---|---|
|
Determine if it is a situation of inverse proportionality. |
|
|\begin{align} k &= \color{blue}{x y} \\ &= \color{blue}{2\times 3} \\ &= 6 \end{align}| |
Find the value of the constant |k| according to |k = xy.| |
|
|\begin{align} k &= x y \\ 6 &= \color{green}{5} y \\ 1{.}2 &= y \end{align}| |
Replace |k| with |6| and |x| with |\color{green}{5}| to isolate |y.| |
|
In this situation, each winner would get the sum of |1{.}2| million dollars. |
|
See also
Knowing the names of each of the components in an algebraic expression helps in understanding their specific roles. These components have specific names:
-
Unknown: Desired numeric value.
-
Variable: Letter used to identify the unknown.
-
Coefficient: Multiplicative factor placed in front of the unknown.
-
Terms: Parts of an expression or equation that are separated by addition or subtraction.
-
Constant term (constant): Term consisting only of a number or where no variable appears.
-
Like terms: Terms made up of the same variables that are also assigned the same exponents.
-
Algebraic expression: Combination of several terms where the total is not known (no = sign).
-
Degree: In a monomial, it corresponds to the sum of the variables’ exponents. In a polynomial, it corresponds to the highest degree among the monomials of which it is composed.
-
Algebraic equation: Combination of several terms with a known result (with an = sign).
In the following algebraic expression: ||\color{blue}{-4x^3y} \color{red}{+3x^2} \color{fuchsia}{-\frac{3}{4} xy^4 } \color{green}{+ 9} \color{orange}{- 4xy^4}|| identify the following:
A) A constant term.
B) If it is an expression or an equation.
C) Its degree.
D) Like terms, if applicable.
E) The coefficient of the 2nd term.
|
ANSWERS |
JUSTIFICATIONS |
|---|---|
|
A) |9| |
Since it is the only term composed of a number without a variable. |
|
B) Algebraic expression |
Since the total of all the terms is unknown (no = sign). |
|
C) |5| |
By finding the sum of the variables’ exponents for each term, we obtain |5| as the greatest total |(\color{orange}{-4xy^4} =- 4x^1y^4 \Rightarrow 1 + 4 = 5).| |
|
D) |\color{fuchsia}{-\frac{3}{4}xy^4}| and |\color{orange}{-4xy^4}| |
They have the same variables and are assigned the same exponents. |
|
E) |3| |
|2^{nd}| term |= \color{red}{ \underline{+3}x^2} \Rightarrow \color{red}{\underline{3}}| is the coefficient. |
See also
To simplify an algebraic expression, follow the order of operations:
-
Multiplication and division: Apply to the coefficients, regardless of the terms.
-
Addition and subtraction: Apply to the coefficients of like terms.
-
Evaluating an algebraic expression: Substitute the variables by the values given.
To be more efficient, a company streamlines monthly revenues using the following algebraic expression: ||\displaystyle 2(4x^2-6) - \frac{1}{2}x^2 + (12x - 1) \div 4||
where |x = |number of hours worked by all employees
What is the income earned from a total of |325| hours worked in a month?
|
CALCULATIONS |
JUSTIFICATIONS |
|---|---|
|
||\begin{align} &\underline{2(4x^2-6)} - \frac{1}{2}x^2 + (12x - 1) \div 4 \\\\ =\ &8x^2-12-\frac{1}{2}x^2 +\underline{(12x-1)\div 4} \\\\ =\ &\color{blue}{8x^2}\color{red}{-12}\color{blue}{-\frac{1}{2}x^2} + 3x \color{red}{- \frac{1}{4}} \\\\ =\ &\color{blue}{\frac{15}{2}x^2}+3x \color{red}{-\frac{49}{4}} \end{align}|| |
Simplify the algebraic expression. |
|
||\begin{align} \text{Profit} &=\color{blue}{\frac{15}{2} (325)^2}+3 (325) \color{red}{-\frac{49}{4}} \\\\ &= \color{blue}{792 \ 187{.}5} + 975 \color{red}{-12{.}25} \\\\ &= $793 \ 150{.}25\ \end{align}|| |
Substitute |x| with |325| and calculate the final total. |
|
The company can expect revenues of |$793 \ 150{.}25.| |
|
See also
Generally, a problem using algebra can be solved by following these steps:
-
Identify the variables and unknowns.
-
Create the equation according to the context of the situation.
-
Simplify the resulting equation.
-
Solve the equation by isolating the variable.
-
Validate the answer using the initial equation.
For your class's gift exchange activity, you need to buy some food for the group meal, some paper plates, and a gift for the exchange that will take place after the meal.
After reviewing your bills, you realize that the food cost |$12| more than triple the amount for the plates, and you spent half the sum of the cost of the plates and food on your gift.
You spent exactly |$36| in total. Determine the amount of each of the three purchases.
|
CALCULATIONS |
JUSTIFICATIONS |
|---|---|
|
|\begin{align} \color{orange}{x} &= \text{Cost of the plates} ($) \\ \color{fuchsia}{3x + 12} &= \text{Cost of the food} ($) \\ \color{blue}{\displaystyle \frac{(3x+12)+x}{2} } &= \text{Cost of the gift}($) \end{align}| |
Identify the unknowns and variables. |
|
|36 =\color{orange}{ x} +\color{fuchsia}{(3x+12)} + \color{blue}{\displaystyle \frac{(3x+12)+x}{2}}| |
Create the equation. |
|
|36 = x + 3x + 12 + \displaystyle \frac{4x+12}{2}| |
Simplify the equation. |
|
|\begin{align} 36 \color{red}{-18} &= 6x + 18 \color{red}{-18} \\ \displaystyle \frac{18}{ \color{red}{6}} &= \frac{6x}{\color{red}{6}} \\ \color{green}{3} &= \color{green}{x} \end{align}| |
Solve the equation by isolating the variable. |
|
|\begin{align} 36 &= x +(3x+12) + \dfrac{(3x+12)+x}{2} \\ \Rightarrow\ 36 &\overset{?}{=} \color{green}{3} + (3\times \color{green}{3}+12) + \dfrac{(3\times \color{green}{3}+12)+\color{green}{3}}{2} \\ 36 &\overset{?}{=} 3 + 9 + 12 + \dfrac{24}{2} \\36 &= 36 \end{align}| |
Validate by substituting the value of |x| in the initial equation. |
|
Thus, the cost for the plates |= \color{orange}{x = $3},| |
|
See also
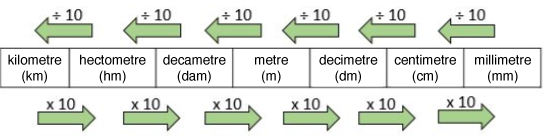
Length Units
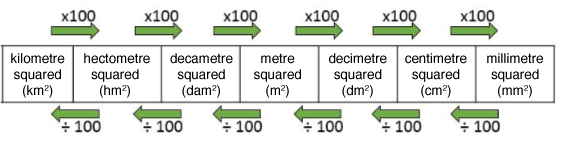
Area Units
What is the measurement, in |\text{m}^2,| of a triangle with a base measuring |\color{blue}{ 820 \ \text{cm}}| and a height of | \color{red}{1{.}2 \ \text{dam}}|?
|
CALCULATIONS |
JUSTIFICATIONS |
|---|---|
|
||\begin{align} \color{blue}{820 \ \text{cm}} &= (820 \div 100) \ \text{m} \\ &= \color{blue}{8{.}2 \ \text{m}} \\\\ \color{red}{1{.}2 \ \text{dam}} &= (1{.}2 \times 10) \ \text{m} \\ &= \color{red}{12 \ \text{m}} \end{align}|| |
Convert all units into metres since the result must be in square metres. |
|
||\begin{align} A_\text{triangle} &= \displaystyle \frac{\color{blue}{b} \times \color{red}{h}}{2} \\ &= \displaystyle \frac{\color{blue}{8{.}2} \times \color{red}{12}}{2} \\ &= 49{.}2 \ \text{m}^2 \end{align}|| |
Apply the formula for the area of a triangle. |
|
The area for the triangle is |49{.}2 \ \text{m}^2.| |
|
See also
To define various plane figures and find missing measurements, reference is made to particular types of lines and line segments:
-
|\color{blue}{\text{Diagonal}\ (\overline{BD})}|: Line segment that connects two vertices which are not adjacent.
-
|\color{red}{\text{Median} \ (\overline{DF})}|: Line segment that connects a vertex with the midpoint of its opposite side.
-
|\color{green}{\text{Perpendicular bisector}\ (\overline{FH})}|: Line segment that is perpendicular to another segment and which divides the latter into two equal parts.
-
|\color{fuchsia}{\text{Bisector}\ (\overline{DE})}|: Line segment that divides an angle into two equal parts.
-
|\color{orange}{\text{Height}\ (\overline{DG})}|: Line segment starting from the vertex of a figure or a solid that is perpendicular to its base.
Associate each type of line segment with an element in the illustration below.
A) Identify a median.
B) Identify a perpendicular bisector
C) Identify a height.
D) Identify a bisector.
|
ANSWERS |
JUSTIFICATIONS |
|---|---|
|
A) Median: |\color{fuchsia}{\overline{AF}}| |
It is the only line segment that connects a vertex with the midpoint on its opposite side. |
|
B) Perpendicular bisector: |\color{red}{\overline{IJ}}| |
It is the only line segment that is perpendicular and in the middle of one side of the polygon |(\overline{BC}).| |
|
C) Height: |\overline{AE}| |
It is the only segment that perpendicularly connects a segment and the vertex that is furthest away. |
|
D) Bisector: |\color{green}{\overline{DM}}| |
It is the only line segment that divides an angle into two equal parts. |
Regular polygons all have the same properties:
-
Every side has the same measurement.
-
Every angle has the same measurement.
-
The sum of the interior angles can be calculated using the formula: |(n-2) \times 180°|, where |n| is the number of sides.
-
They are formed by a set of isosceles triangles, except the hexagon that is formed by equilateral triangles.
-
They each have a different name depending on the number of sides.
-
The apothem is the line segment connecting the center of the polygon with the midpoint of one of its sides.
-
The apothem is perpendicular to the side it touches.
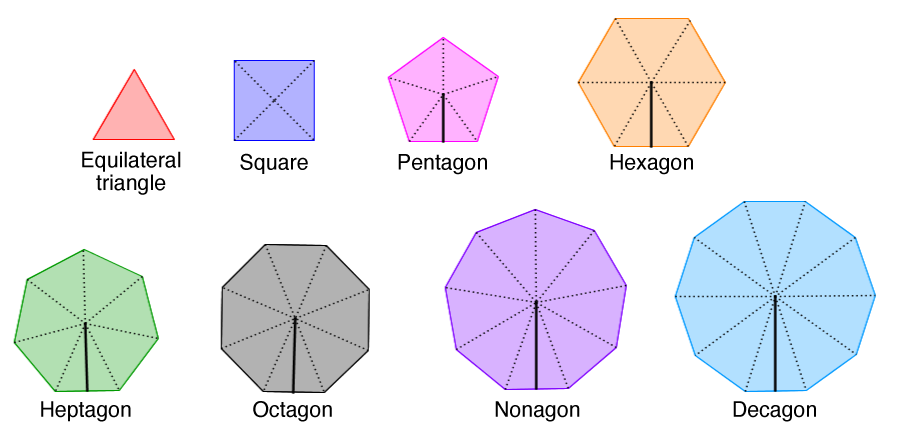
True or false: a regular octagon with a side measurement of |\color{red}{8 \ \text{cm}}| has a larger perimeter than a regular decagon with one side measuring |\color{blue}{7 \ \text{cm}}.|
|
CALCULATIONS |
JUSTIFICATIONS |
|---|---|
|
|\begin{align} P_\text{octagon} &= \color{red}{s} \times n \\ &= \color{red}{8} \times 8 \\ &= 64 \ \text{cm} \end{align}| |
Calculate the perimeter of the regular octagon. |
|
|\begin{align} P_\text{decagon} &= \color{blue}{s} \times n \\ &= \color{blue}{7} \times 10 \\ &= 70 \ \text{cm} \end{align}| |
Calculate the perimeter of the regular decagon. |
|
The statement is false because |70 > 64\ \Rightarrow\ P_\text{decagon} > P_\text{octagon}| |
|
See also
To clearly distinguish the properties of different line segments in a circle, use the following terms:
-
|\color{orange}{\text{Chord} \ (\overline{CF})}|: Line segment which connects any two points on the circle.
-
|\color{red}{\text{Diameter}\ (\overline{DE})}|: Line segment which connects any two points of the circle passing through the centre.
-
|\color{green}{\text{Radius} \ (\overline{AO})}|: Generally noted |r| , it is a line segment which connects the centre of the circle to any point on the circle.
-
Circumference of a Circle |=| outline of the circle |= 2 \pi r.|
-
|\color{fuchsia}{\text{Arc of the circle} \ \overset{\huge\frown}{\small {AB}}}|: Curve joining two points on the circumference of the circle
||\displaystyle \frac{\color{fuchsia}{m \overset{\huge\frown}{\small {AB}}}}{\color{fuchsia}{m \ \angle AOB}} = \displaystyle \frac{\text{Circumference}}{360^\circ}|| -
Area of a Circle |=| surface covered by a disc |= \pi r^2.|
-
Area of a Sector: Portion of the circle which is delimited by two radii. ||\displaystyle \frac{\text{Area of the sector} AOB}{\text{Area of the circle}}= \displaystyle \frac{\color{fuchsia}{m \ \angle AOB}}{360^\circ}||
Cowboys use lassos to capture cattle. Lassos are made up of two parts: a rope and a loop. When the loop is undone, a professional cowboy wraps the lasso around his body eight times before placing it on a hook. The length necessary to make one loop corresponds to an arc of a circle intercepted by a central angle of |\color{red}{325^\circ}.|
What is the length of the rope, i.e., the part of the lasso without the loop?
|
CALCULATIONS |
JUSTIFICATIONS |
|---|---|
|
||\begin{align} \dfrac{\color{fuchsia}{\text{m arc of the circle}}}{\text{m central angle}} &= \dfrac{\text{Circumference}}{360^\circ} \\ \Rightarrow\ \dfrac{\color{fuchsia}{\text{m arc of the circle}}}{\color{red}{325^\circ}} &= \displaystyle \frac{2 \pi (\color{blue}{40}\div 2)}{360^\circ} \\\\ \Rightarrow\ \ \color{fuchsia}{\text{m arc of the circle}} &= \displaystyle \frac{\color{red}{325^\circ} \times 2 \pi (20)}{360^\circ} \\ &\approx \color{fuchsia}{113{.}45 \ \text{cm}} \end{align}|| |
Determine the size of the arc of the circle. |
|
||\begin{align} \color{green}{\text{Initial length}} &= 8 \times \text{Circumference} \\ &= 8 \times 2 \pi (\color{blue}{40} \div 2) \\ &\approx \color{green}{1 \ 005{.}31 \ \text{cm}} \end{align}|| |
Determine the initial length of the lasso. |
|
||\begin{align} \text{Final length} &= \color{green}{\text{Initial length}} - \color{fuchsia}{\text{Loop}} \\ &=\color{green}{1 \ 005{.}31} - \color{fuchsia}{113{.}45} \\ &= 891{.}86 \ \text{cm} \end{align}|| |
Determine the final length of the lasso. |
|
By subtracting the size of the loop, the lasso’s length is |891{.}86 \ \text{cm}.| |
|
See also
Since it is a decomposable figure, it is necessary to work with each face’s area. Thus, the area formulas of plane figures will be used.
|
|A_\text{squared} = s^2| |
|A_\text{rectangle} = b\times h| |
|A_\text{rhombus} = \displaystyle \frac{D \times d}{2}| |
|
|A_\text{parallelogram}=b \times h| |
|A_\text{trapezoid} = \displaystyle \frac{(B+b)\times h}{2}| |
|A_\text{triangle} = \displaystyle \frac{b \times h}{2}| |
|
|A_\text{circle}=\pi r^2| |
|A_\text{regular polygon}= \displaystyle \frac{s a n}{2}| |
|
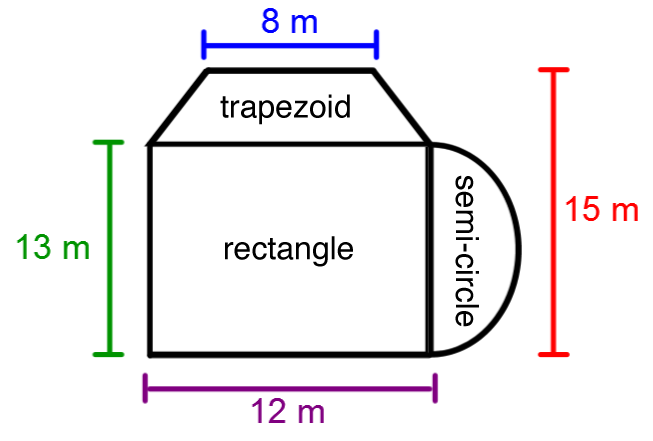
With the winter season coming up, a heavy machinery contractor is submitting bids to win snow removal contracts. To be competitive, he charges |$3{.}50/ \text{m}^2.|
What will be the amount of his bid for the snow removal contract, using the dimensions provided above?
|
CALCULATIONS |
JUSTIFICATIONS |
|---|---|
|
|
Separate the figure into several shapes with known area formulas. |
|
|\begin{align} A_\text{trapezoid} &= \dfrac{ (\color{fuchsia}{B}+\color{blue}{b}) \times h}{2} \\ &= \dfrac{ (\color{fuchsia}{12} + \color{blue}{8}) \times (\color{red}{15}-\color{green}{13})}{2} \\ &= \displaystyle \frac{ 20 \times 2}{2} \\ &= 20 \ \text{m}^2 \end{align}| |\begin{align} A_\text{rectangle} &= \color{fuchsia}{b} \times \color{green}{h} \\ &= \color{fuchsia}{12} \times \color{green}{13} \\ &= 156 \ \text{m}^2 \end{align}| |\begin{align} A_\text{half-circle} &= \dfrac{\pi r^2}{2} \\ &= \dfrac{\pi (\color{green}{13} \div 2)^2}{2} \\ &\approx 66{.}37 \ \text{m}^2 \end{align}| |
Calculate the area of each of the sections. |
|
|\begin{align} A_\text{total} &= A_\text{trapezoid} + A_\text{rectangle} + A_\text{half-circle} \\ &= 20 + 156 + 66{.}37 \\ &= 242{.}37 \ \text{m}^2 \end{align}| |
Calculate the total area of the driveway. |
|
|\begin{align} \text{Final amount} &= 242{.}33 \times 3{.}50 \\ &= $848{.}16 \ \end{align}| |
Calculate the final bid. |
|
The bid amount should be |$848{.}16.| |
|
See also
It is preferable, for a decomposable solid, to work with the area of each face rather than with the total area of each solid used to build it. In other words, the area formulas of plane figures will be used.
|
|A_\text{square} = s^2| |
|A_\text{rectangle} = b\times h| |
|A_\text{rhombus} = \displaystyle \frac{D \times d}{2}| |
|
|A_\text{parallelogram}=b \times h| |
|A_\text{trapezoid} = \displaystyle \frac{(B+b)\times h}{2}| |
|A_\text{triangle} = \displaystyle \frac{b \times h}{2}| |
|
|A_\text{circle}=\pi r^2| |
|A_\text{regular polygon}= \displaystyle \frac{s a n}{2}| |
|
With the holiday season around the corner, you decide to play a prank on your parents by completely wrapping their gift with gray duct tape. To be precise, it is a square prism with a cylinder on top.
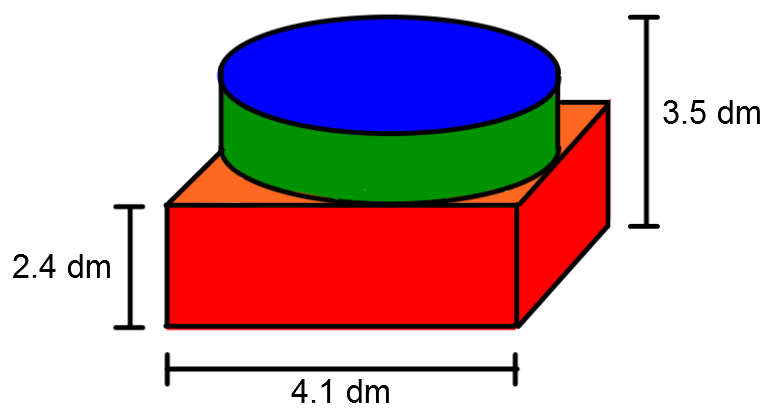
Using the measurements provided in the drawing above, how much tape, in |\text{dm}^2,| will you need?
|
CALCULATIONS |
JUSTIFICATIONS |
|---|---|
|
|\begin{align} \color{red}{A_\text{rectangles}} &= 4 \times (4,1 \times 2{.}4) \\ &= \color{red}{39{.}36 \ \text{dm}^2} \end{align}| |\begin{align} A_\text{underneath} &= 4{.}1^2 \\ &= 16{.}81 \ \text{dm}^2 \end{align}| |\begin{align} \color{orange}{A_\text{top}} &= A_\text{square} - A_\text{circle} \\ &= 4{.}1^2 - \pi (4{.}1 \div 2)^2 \\ &\approx \color{orange}{3{.}61 \ \text{dm}^2} \end{align}| |
Calculate the area of each of the surfaces. |
|
|\begin{align} A_\text{total} &= \color{red}{39{.}36} + 16{.}81 + \color{orange}{3{.}61} + \color{green}{14{.}16} + \color{blue}{13{.}20} \\ &= 87{.}14 \ \text{dm}^2 \end{align}| |
Add the areas of each section. |
|
You must use at least |87{.}14 \ \text{dm}^2| of duct tape. |
|
See also
Use the following steps to find a missing measurement:
-
Identify the measurements given.
-
Determine the formula to use.
-
Replace the known variables.
-
Isolate the desired variable.
A collector sees a chest that they are interested in buying inside an antique store. They need to know the chest’s height, because it must be the same as those which they already own. The total area of the chest was calculated during the restoration process.
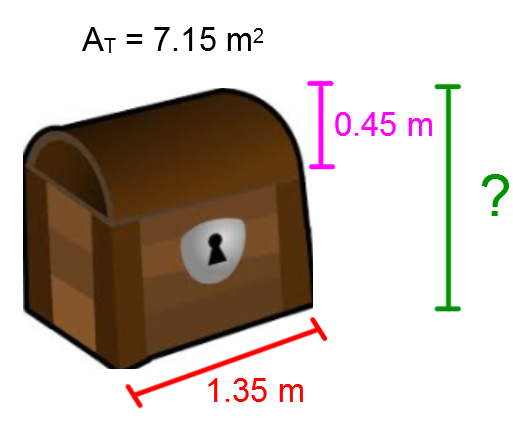
What is the height of the chest?
|
CALCULATIONS |
JUSTIFICATIONS |
|---|---|
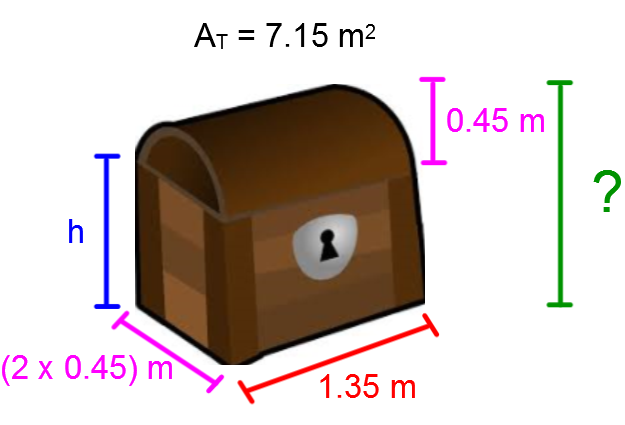 |
Identify the measurements given. |
|
|\begin{align}A_\text{total} =\ &A_\text{base}+2 A_\text{faces left and right}+2 A_\text{faces front and back} \\ &+ \frac{1}{2}A_\text{L cylinder} + A_\text{disc} \\\\ \displaystyle 7{.}15 =\ &\color{red}{1{.}35}\times \color{fuchsia}{0{.}9} + 2 (\color{fuchsia}{0{.}9}\times \color{blue}{h}) + 2 (\color{red}{1{.}35}\times \color{blue}{h}) \\ &+ \frac{1}{2} (2 \pi \times \color{fuchsia}{0{.}45} \times \color{red}{1{.}35}) + \pi\times \color{fuchsia}{0{.}45}^2 \end{align}| |
Determine the formula to use. Replace the known variables. |
|
|\begin{align} 7{.}15 &\approx 1{.}215 + 1{.}8\color{blue}{h} + 2{.}7\color{blue}{h} + 1{.}908+0{.}636 \\ 7{.}15 &\approx 3{.}759 + 4{.}5\color{blue}{h} \\ 3{.}391 &\approx 4{.}5\color{blue}{h} \\ \color{blue}{0{.}75} &\approx \color{blue}{h} \end{align}| |
Isolate the desired variable |(\color{blue}{h}).| |
|
The total height of the chest | \approx \color{blue}{h} + \color{fuchsia}{0{.}45} \approx \color{blue}{0{.}75}+\color{fuchsia}{0{.}45} \approx 1{.}2 \ \text{m}.| |
|
See also
Here are the names of the different types of angles according to their measurements:
-
A zero angle: angle that measures |0^\circ.|
-
An acute angle: angle that measures between |0^\circ| and |90^\circ.|
-
A right angle: Often represented using a black square, it is an angle that measures exactly |90^\circ.|
-
An obtuse angle: angle that measures between |90^\circ| and |180^\circ.|
-
A straight angle: angle that measures exactly |180^\circ.|
-
A reflex angle: angle that measures between |180^\circ| and |360^\circ.|
-
A full (or complete) angle: angle that measures |360^\circ.|
Here are some definitions related to pairs of angles:
-
Adjacent angles: a pair of angles that share a common vertex and side and which are located on either side of the common angle.
-
Complementary angles: two angles where the sum of their measurements is |90^\circ.|
-
Supplementary angles: two angles where the sum of their measurements is |180^\circ.|
Two lines intersected by a transversal form pairs of remarkable angles. If the lines are parallel, several congruent angles can be found.
Thus, |d_1 // d_2| and |d_3,| is a secant, as follows:
The following angles are congruent:
-
Alternate-Interior angles |(\color{redorange}{m\angle BEG} = \color{fuchsia}{m\angle CBE})|: Angles which are on either side of the transversal, that do not share the same vertex, and are inside the parallel lines.
-
Alternate-Exterior angles |(\color{green}{m\angle ABF} = \color{orange}{m\angle DEH})|: Angles which are on either side of the transversal, that do not share the same vertex, and are outside the parallel lines.
-
Corresponding angles |(\color{red}{m\angle ABC} = m\angle BED)|: Angles which are on the same side of the transversal and do not share the same vertex. One angle is inside the parallel lines and the other, outside.
-
Vertically Opposite angles |(\color{blue}{m\angle FBE} = \color{red}{m\angle ABC})|: Angles which share the same vertex and where the sides of one of the angles are the extension of the sides of the other angle.
Finally, to derive angle measurements, it is sometimes helpful to remember that the sum of a triangle’s interior angles is |180^\circ.| For other polygons, apply the following formula:
-
The sum of the interior angles of a polygon |=(n-2)\times 180^\circ| where |n| is the number of the polygon’s sides.
What is |\color{red}{m\angle CBL}| in the following drawing?
The following is one of the many possible steps to answer the question:
|
CALCULATIONS |
JUSTIFICATIONS |
|---|---|
|
|m\angle GJC = m\angle QJP=43^\circ| |
They are vertically opposite angles. |
|
|m\angle BHG = m\angle MHG=90^\circ| |
These are adjacent supplementary angles: |\begin{align} m\angle BHG &= 180^\circ - m\angle GHM \\ &= 180^\circ - 90^\circ \\ &= 90^\circ \end{align}| |
|
|m\angle JGC = m\angle BHG = 90^\circ| |
Two parallel lines |(IK // ML)| intersected by a transversal |(PN)| form corresponding congruent angles. |
|
|m\angle JCG = 47^\circ| |
In any triangle, the sum of the interior angles is |180^\circ.| Thus, in the triangle |JCG,| we have: |
|
|m\angle GCB = 133^\circ| |
It is supplementary to |\angle JCG:| |\begin{align} 180^\circ &= m\angle JCG + m\angle GCB \\ 180^\circ &= 47^\circ + m\angle GCB \\133^\circ &= m\angle GCB \end{align}| |
|
|\begin{align} \color{red}{m \angle CBL} =m\angle GCB = \color{red}{133^\circ} \end{align}| |
Two parallel lines |(IK // ML)| intersected by a transversal |(QB)| form alternate-interior congruent angles. |
See also
Denoted |t_{(x,y)}|, a translation is an isometry since the measurements of the angles and corresponding sides remain identical.
A translation is generally defined by a translation arrow.
Using your geometry tools, perform the following translation:
|
CALCULATIONS |
JUSTIFICATIONS |
|---|---|
|
Draw lines parallel to the translation arrow for each of the vertices. |
|
|
Measure the length of the translation arrow. |
|
|
Use this same measurement to determine the location of each of the vertices in the image. |
|
|
Connect the vertices in the image (same letters but accompanied by the symbol ') in the same order as the vertices of the initial image. |
See also
Denoted |r_{(O,\text{degree})}|, a rotation is an isometry because the measurements of the angles and corresponding sides remain the same.
The rotation is defined by an angle of rotation.
Using your geometry tools, perform the rotation below.
|
CALCULATIONS |
JUSTIFICATIONS |
|---|---|
|
From the centre of rotation, draw a circle for each of the vertices using a compass. |
|
|
For each of the circles, measure the opening corresponding to the circular arc of each of the vertices. |
|
|
Transpose this measurement from the vertex. |
|
|
Repeat the previous two steps for each of the vertices. |
|
|
Connect the vertices of the image in the same order as in the initial figure. |
See also
Denoted |s_{\text{axis}}|, a reflection (symmetry) is an isometry since the measurements of the angles and corresponding sides remain the same.
A reflection is defined by a line of symmetry.
Using your geometric tools, perform the following reflection:
|
CALCULATIONS |
JUSTIFICATIONS |
|---|---|
|
Draw lines perpendicular to the line of reflection from each of the vertices. |
|
|
Measure the distance between the line of reflection and one vertex. |
|
|
Transfer the measurement to the same perpendicular line, but on the other side of the line of reflection. |
|
|
Repeat the previous two steps for each of the vertices. |
|
|
Connect vertices’ images in the same order as in the initial figure. |
See also
|h_{(O,k)}| establishes a similarity between the two figures since the corresponding angles are congruent and the corresponding sides are proportional.
Using your geometry tools, perform the dilation given by |h_{(O; 1,5)}|.
|
CALCULATIONS |
JUSTIFICATIONS |
|---|---|
|
Draw a straight line connecting the centre of dilation |O| to each of the vertices. |
|
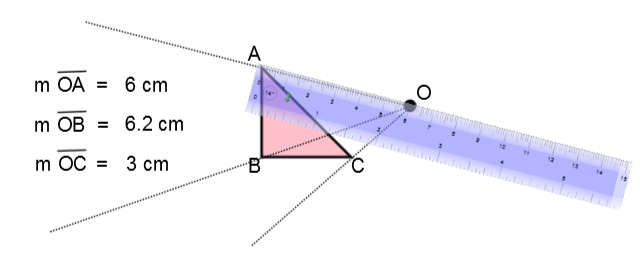 |
Measure the distance between the centre of dilation |O| and each of the vertices. |
|
|\begin{align} \text{m}\overline{OA'}&= \color{blue}{m\overline{OA}}\cdot\color{red}{k} \\ \Rightarrow\ \text{m} \overline {OA'} &= \color{blue}{6} \times \color{red}{1{.}5} \\ \Rightarrow\ \text{m} \overline{OA'} &= 9\ \text{cm} \\\\ \text{m}\overline{OB'} &= 9{.}3 \ \text{cm} \\ \text{m}\overline{OC'} &= 4{.}5 \ \text{cm} \end{align}| |
Apply the scale factor to each of the measured distances. |
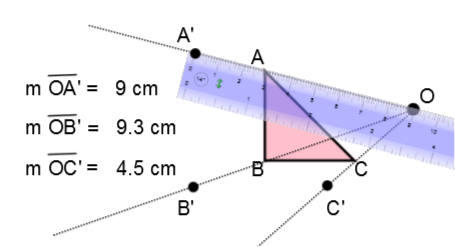 |
Identify the image’s vertex using the distance calculated from the centre of dilation |O| . |
|
Connect each of the image vertices in the same order as in the initial figure. |
See also
All Cartesian planes have the same characteristics:
-
Quadrants: they represent each of the four divisions of the Cartesian plane.
-
The x- axis: horizontal axis associated with the independent variable |(x).|
-
The y- axis: vertical axis associated with the dependent variable |(y).|
-
The origin: meeting point of the two axes with the coordinate |(0,0).|
-
Coordinates |(x,y)|: any point on the Cartesian plane has a pair of coordinates based on its value on the x-axis |x| and the y-axis |y.|
-
The axes: each of the axes is represented by a graduated straight line.
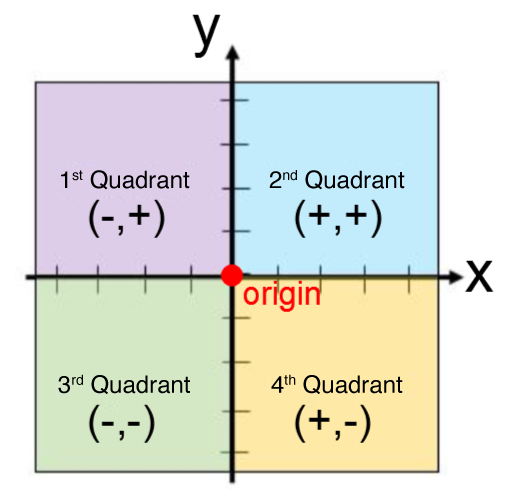
Place each of the following points on the Cartesian plane: ||A(2,3),\ B(-3,2),\ C(-2,-3),\ D(4,-2)||
See also
To fully understand probability, it is important to differentiate between different types events:
-
Impossible: probability is equal to 0 (0%).
-
Certain: probability is 1 (100%).
-
Probable: probability is between 0 and 1 (between 0% and 100%).
-
Elementary: contains a single element.
-
Compatible/Incompatible: events where intersection is not empty/intersection is empty.
-
Dependent/Independent: when the 2nd draw’s outcome is influenced by the 1st draw or when the 2nd draw’s outcome is not influenced by the 1st draw.
Different situations will determine the qualifiers that are most appropriate for each.
1) A: Drawing an ace from a 52-card deck.
B: Drawing a king from another deck of 52 cards.
2) Rolling eight on a six-sided die.
3) Pick two balls consecutively without returning them to a basket containing 30 balls.
|
CALCULATIONS |
JUSTIFICATIONS |
|---|---|
|
1) Incompatible and independent events. |
Incompatible: The two events have nothing in common. |
|
2) Impossible event. |
Impossible: Since the faces of the die are numbered from 1 to 6, it is impossible to roll eight. |
|
3) Incompatible and dependent events. |
Incompatible: It is impossible to draw the same ball twice. |
See also
As in many fields, theory and practice often give two different results:
-
Experimental probability: Probability that is obtained following an experiment.
-
Theoretical probability: Probability that is obtained as a result of the theoretical analysis of the possible outcomes.
Study the following situation and decide if it refers to experimental or theoretical probability.
A) To determine the probability of obtaining a head or a tail when tossing a coin, Julian flips one 50 times and records each of the results. In the end, he gets |P(\text{tails}) = \displaystyle \frac{23}{50}| and |P(\text{heads})=\displaystyle \frac{27}{50}|.
B) Since a regular die has six identical sides, we can determine the following: |P(1) = P(2) = P(3) = P(4) = P(5) = P(6) = \displaystyle \frac{1}{6}.|
|
CALCULATIONS |
JUSTIFICATIONS |
|---|---|
|
A) Experimental |
Since the probability is established following an experiment, it is experimental probability. |
|
B) Theoretical |
Since the probability is determined by calculations or according to the analysis of the situation, without an experiment, it is theoretical probability. |
See also
||\mathbb{P} = \displaystyle \frac{\text{Number of desired results}}{\text{Total number of possible results}}||
In addition, the number of possible results will be influenced if the draw is made with or without replacement.
To win the grand prize in a neighborhood festival, competitors must draw two black balls one after the other. They can do it one of two ways.
A) Draw from a basket containing 10 balls without returning them: five are red, three are green and two are black.
B) Draw from a basket containing 15 balls and replace the ball after the first draw: seven are red, five are green and three are black.
To maximize the odds, which approach should the competitors choose?
|
CALCULATIONS |
JUSTIFICATIONS |
|---|---|
|
A) ||\begin{align} P(\text{black followed by a black}) &= \dfrac{2}{10}\times \dfrac{1}{9} \\ &= \dfrac{2}{90} \\ &= \dfrac{1}{45} \\ &\approx 2{.}2\ \% \end{align}|| |
Calculate the probability, considering that the 1st ball is not replaced in the basket for the 2nd draw. |
|
B) ||\begin{align} P(\text{black followed by a black}) &= \dfrac{3}{15} \times \dfrac{3}{15} \\ &= \dfrac{9}{225} \\ &= \dfrac{1}{25} \\ &= 4\ \% \end{align}|| |
Calculate the probability, considering that the 1st ball is replaced in the basket for the 2nd draw. |
|
Approach B) is the better strategy since the probability of winning is higher |\big(P(A) = 4\ \% > P(B) \approx 2{.}2\ \%\big).| |
|
See also
Here are two sampling methods that are frequently used:
-
Random: Elements are chosen at random, without a precise methodology.
-
Systematic: Elements are chosen respecting a precise frequency.
Identify the method that is the most appropriate for each situation.
1) Quality control in a factory checks 1 out of every 100 items that leave the production line.
2) To try to predict the results of the next election, we conduct a poll by asking people at a shopping mall entrance.
|
CALCULATIONS |
JUSTIFICATIONS |
|---|---|
|
1) Systematic |
Quality control is carried out on a regular basis (1 out of every 100). |
|
2) Random |
People interviewed are chosen at random, i.e., without taking into account a specific characteristic or frequency. |
See also
To ensure the credibility of a survey, certain pitfalls should be avoided during the setup, completion, and analysis of the survey data. For example, the following sources of bias are common:
-
Sample size: ensure that enough people are interviewed so that the results are representative of the population.
-
Formulation of questions: Ensure that the questions do not suggest a position or specific opinion (i.e., avoid leading questions).
In the following situations, indicate whether the question is biased or not. If yes, identify the source of the bias.
A) To find out what people think of the town hall expansion, the mayor sends a survey by mail to 1 000 of the 5 000 residents.
B) The following question is asked: "Do you not agree with the fact that a company should not move its head office to avoid losing certain tax advantages?"
|
CALCULATIONS |
JUSTIFICATIONS |
|---|---|
|
A) No bias: |
Getting responses from 1 000 people is adequate in terms of credibility. |
|
B) Bias: Formulation of the question. |
The question is confusing because of the use of double negatives. |
See also
In general, we can define the type of variable studied using the following qualifiers:
-
Qualitative: When the answer is a word or a phrase.
-
Quantitative Discrete: When the answer is a numerical value that is a whole number (belonging to the set of integers |(\mathbb{Z}).|)
-
Quantitative Continuous: When the answer given is a numerical value that can have decimal form (belonging to the set of real numbers |(\mathbb{R}).|)
Identify the type of variable being studied in the following situations.
A) People are asked about their favourite pet.
B) People are asked how many pets they have in their homes.
|
CALCULATIONS |
JUSTIFICATIONS |
|---|---|
|
A) Variable studied: Pets. |
The answer to this question will always be a word or the kind of the pet (i.e., dog, cat, bird, and so on). |
|
B) Variable studied: Number of animals. |
The answer to the question will be a whole number. |
See also
Once the data has been collected, it must be analyzed to draw satisfactory conclusions. To do that, some numerical values can be used:
-
Mean |= \displaystyle \frac{\text{Sum of data}}{\text{Total number of data}}|
-
Range |= \text{Maximum value} - \text{Minimum value}|
-
Minimum |= \text{Smallest value in the distribution}|
-
Maximum |= \text{Largest value in the distribution}|
To have an idea of the sizes for the sportswear that a school wants to provide to different team members, |\color{blue}{20}| students were asked to give their measurements. Here are the results obtained about the sizes (in cm) of each student:
|\color{green}{120,}| |\color{red}{124,}| |\color{red}{124,}| |\color{red}{ 125,}| |\color{red}{127,}| |\color{red}{128,}| |\color{red}{129,}| |\color{red}{130,}| |\color{red}{131,}| |\color{red}{134,}| |\color{red}{134,}| |\color{red}{134,}| |\color{red}{141,}| |\color{red}{142,}| |\color{red}{142,}| |\color{red}{143,}| |\color{red}{145,}| |\color{red}{147,}| |\color{red}{148,}| |\color{fuchsia}{149}|
Using this distribution, determine the mean and range.
|
CALCULATIONS |
JUSTIFICATIONS |
|---|---|
|
||\begin{align} \text{Mean} &= \dfrac{\color{green}{120}\color{red}{+124+\dots+148}\color{fuchsia}{+149}}{\color{blue}{20}} \\ &= 134{.}85 \ \text{cm} \end{align}|| |
Apply the formula. |
|
||\begin{align} \text{Range} &= \color{fuchsia}{\text{max}} - \color{green}{\text{min}} \\ &= \color{fuchsia}{149}-\color{green}{120} \\&= 29\ \text{cm} \end{align}|| |
Identify the maximum |(149)| and minimum |(120)| values to apply to the formula. |
|
The average size is |134{.}85 \ \text{cm},| while the value of the range is |29\ \text{cm}.| |
|
See also
Use the following list to ensure that all elements are included when setting up a bar graph.
-
Build a distribution table.
-
Label the axes and give the title of the graph.
-
Ensure that an appropriate scale (graduation) is used and enough space is available to write the different terms/values of the survey.
-
Associate the size of the bars with the frequency of each of the terms/values.
People at the entrance to a shopping centre are asked about the number of gifts they are thinking of giving to members of their family. The following answers were obtained:
|3,| |4,| |2,| |6,| |5,| |3,| |5,| |6,| |1,| |4,| |1,| |5,| |4,| |6,| |8,| |5,| |6,| |8,| |4,| |5,| |3,| |6,| |2,| |4,| |5,| |2,| |6,| |5,| |3,| |2|
To have a better idea of people's intentions, display the data using a bar graph.
|
CALCULATIONS |
JUSTIFICATIONS |
|---|---|
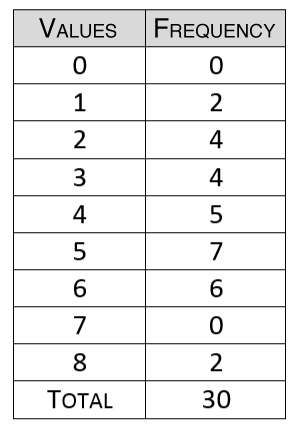 |
1) Build a distribution table. |
 |
2) Identify the title and axes of the graph. |
 |
3) Graduate the two axes appropriately. |
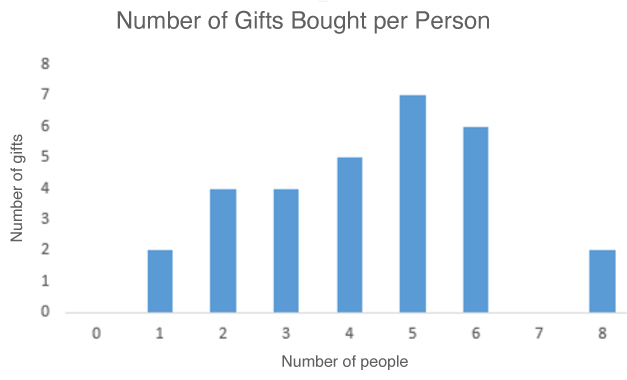 |
4) Draw the horizontal or vertical bars (your choice). |
See also
Use the list below to ensure all elements are included when setting up a pie chart.
-
Build a distribution table with the corresponding central angles.
|
Terms or values |
Number |
Relative Frequency(%) |
Central Angle (°) |
|---|---|---|---|
|
According to answers given |
Enumeration of each term/value |
|\displaystyle \frac{\text{Frequency of number analyzed}}{\text{Total frequency}} \times 100| |
|\displaystyle \frac{\text{Frequency}}{100 \%} = \frac{\text{m of the angle}}{360^\circ}| |
-
Draw each of the sectors using their respective central angles.
-
Add a legend and a title.
-
Make sure the percentages are written in each of the sectors.
To obtain a global perspective of the company's investment income, the general manager wants you to arrange the following information in a pie chart: ||\begin{align} \color{blue}{\text{Salary}} &= \color{blue}{$1 \ 190 \ 000} \\ \color{orangered}{\text{Electricity}} &= \color{orangered}{$420 \ 000} \\ \color{gray}{\text{Heating}} &= \color{gray}{$315 \ 000} \\ \color{orange}{\text{Marketing}} &= \color{orange}{$700 \ 000} \\ \color{darkblue}{\text{Investments}} &= \color{darkblue}{$245 \ 000} \\ \color{green}{\text{Renovations}} &= \color{green}{$630 \ 000} \end{align}||
Here’s your chance!
|
CALCULATIONS |
JUSTIFICATIONS |
|---|---|
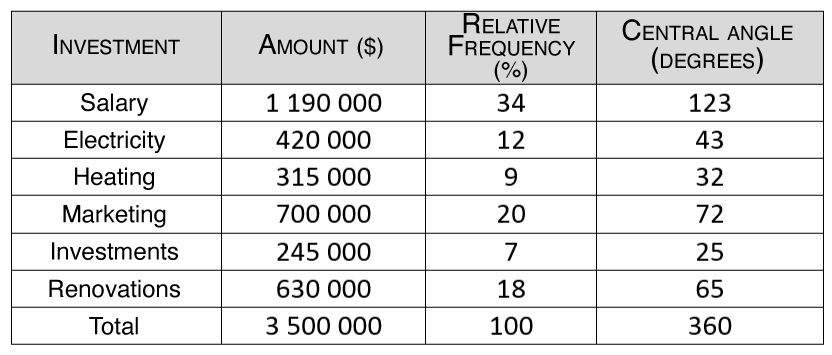 |
1) Build the distribution table. ||\begin{align} \% = \displaystyle \frac{\text{Amount} \times 100}{3\ 500\ 000} \\ \text{Angle} = \displaystyle \frac{\text{Amount}\times 360}{3\ 500\ 000} \end{align}|| |
 |
2) Draw the sectors. |
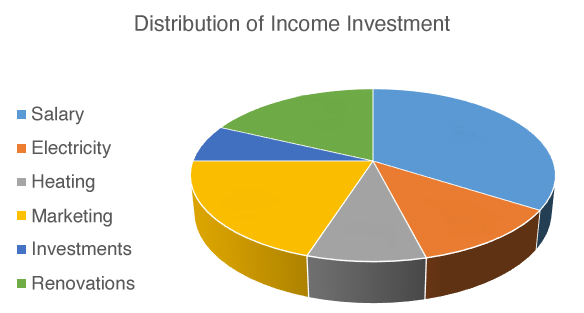 |
3) Add a legend and a title. |
 |
4) Add the percentages for each of the sectors. |