Voici un petit guide de préparation contenant toutes les notions abordées en troisième secondaire. Pour expliquer le tout, chaque formule sera suivie d'un exemple et d'un lien qui mène à une fiche de notre bibliothèque virtuelle.
Pour cette section, il est important de différencier les ensembles suivants :
|\mathbb{N} = | nombres naturels : nombres entiers positifs.
|\mathbb{Z} = | nombres entiers : nombres entiers positifs et négatifs.
|\mathbb{Q} = | nombres rationnels : nombres que l'on peut écrire en fraction de la forme |\frac{a}{b}| avec |\{a, b\} \in \mathbb{Z}| et |b \neq 0.|
|\mathbb{Q}' = | nombres irrationnels : nombres qu'on ne peut pas écrire en fraction de la forme |\frac{a}{b}| avec |\{a,b\} \in \mathbb{Z}| et |b \neq 0.|
|\mathbb{R} = | nombres réels : ensemble de nombres qui regroupe tous les ensembles présentés plus haut.
Pour être plus spécifique, on peut également utiliser les indices « * » , « + » et « - » pour respectivement faire référence à un ensemble ne contenant pas le nombre 0, seulement les nombres positifs ou seulement les nombres négatifs. (ex: |\mathbb{N} = \mathbb{Z}_+|)
Quel est le plus petit ensemble de nombres qui inclut tous les nombres suivants : ||\{0{,}125\ ,\ 19\ \%\ ,\ 0{,}\overline{666}\ ,\ 30\}||
| CALCULS | JUSTIFICATIONS |
|---|---|
|
||\begin{align} 0{,}125 &= \dfrac{125}{1000} = \dfrac{1}{8} \\ 19\ \% &= \dfrac{19}{100}\\ 0{,}\overline{666} &= \dfrac{2}{3} \end{align}|| |
|\{0{,}125 ; 19\ \% ; 0{,}\overline{666}\} \in \mathbb{Q},| car on peut tous les écrire sous la forme d'une fraction |\dfrac{a}{b}| avec |\{a,b\} \in \mathbb{Z}.| |
|
|30| |
|30 \in \mathbb{N},| car c'est un entier positif. |
|
Puisque tous ces nombres sont positifs et que le |0| n'est pas mentionné, on peut dire que le plus petit ensemble qui les regroupe est |\mathbb{Q}^*_+.| |
|
À voir aussi
Pour l'écriture de ces sous-ensembles, il est important de respecter les différentes conventions d'écriture :
Intervalles : Utilisation des crochets pour indiquer le début et la fin du sous-ensemble.
Extension : Utilisation des accolades pour énumérer tous les nombres du début jusqu'à la fin du sous-ensemble. S'il est infini, on peut utiliser les points de suspension (...).
Droite numérique : Utilisation de la droite numérique pour représenter le début et la fin du sous-ensemble.
Utilise les trois méthodes d'écriture pour représenter le sous-ensemble suivant : ||-3 < x \leq 2{,}5||
| CALCULS | JUSTIFICATIONS |
|---|---|
|
Intervalles ||x \in\ ]-3;\ 2{,}5]|| |
Puisque |-3| est exclu, on utilise un crochet ouvert |(\ ]\ )| et pour identifier que le |2{,}5| est inclus, on utilise le crochet fermé |(\ ]\ ).| |
|
Droite numérique |
En dessinant une droite numérique, on utilise le point fermé |(\bullet)| pour les nombres qui sont inclus et le point ouvert pour les nombres exclus |(\circ).| |
|
Dans le cas présent, il est impossible d'utiliser la notation par extension étant donné qu'il est impossible d'écrire tous les nombres qui existent entre |-3| et |2{,}5.| |
|
À voir aussi
Pour écrire un nombre en notation scientifique, on utilise la notation |a \times 10^b| avec |1\leq a <10| et |b \in \mathbb{Z}.|
Addition et soustraction
-
S'assurer que la valeur du |b| est la même pour chacun des termes.
-
Effectuer l'opération sur les coefficients |a.|
-
Au besoin, modifier l'exposant |b| afin que |1 \leq a <10.|
Multiplication et division
-
Effectuer l'opération sur les coefficients |a.|
-
Appliquer les lois des exposants sur les exposants |b.|
-
Au besoin, modifier la valeur finale du |b| pour s'assurer que |1 \leq a < 10.|
Quel est, en notation scientifique, le résultat de la chaine d'opérations suivante : ||(2{,}1 \times 10^5 + 4{,}2 \times 10^4) \times 8{,}43 \times 10^{12}||
| CALCULS | JUSTIFICATIONS |
|---|---|
|
||\begin{align} &(\color{red}{2{,}1 \times 10^5} + 4{,}2 \times 10^4) \times 8{,}43 \times 10^{12} \\ =\ &(\color{red}{21 \times 10^4} + 4{,}2 \times 10^4) \times 8{,}43 \times 10^{12} \\ =\ &\color{blue}{25{,}2} \times 10\color{green}{^4} \times \color{blue}{8{,}43} \times 10\color{green}{^{12}} \end{align}|| |
Modifier les termes qui s'additionnent afin que leur exposant ait la même valeur. |
|
||\begin{align} |
Multiplier les coefficients et appliquer la loi des exposants appropriée. |
|
||=2{,}124 \ 36 \times 10^{18}|| |
Modifier la valeur de l'exposant afin que le coefficient |\in [1,10[.| |
|
Le résultat est |2{,}124 \ 36 \times 10^{18}.| |
|
À voir aussi
Pour être en mesure de simplifier des expression exponentielles, il faut se souvenir des lois des exposants :
|
|\left(\dfrac{a}{b}\right)^{-m} = \left(\dfrac{b}{a}\right)^m| |
|(ab)^m = a^m b^m| |
|
|a^{\frac{m}{n}} = \sqrt[n]{a^m}| |
|\left(\dfrac{a}{b}\right)^m = \dfrac{a^m}{b^m}| |
|
|a^m \times a^n = a ^{m+n}| |
|(a^m)^n = a^{m n}| |
|
|\dfrac{a^m}{a^n} = a^{m-n}| |
|a^0=1| |
Détermine si les deux expressions exponentielles suivantes sont égales : ||\left(\dfrac{36c^4d^6}{e^8} \right)^{\frac{-1}{2}} = \dfrac{e^4}{18c^2d^3}||
| CALCULS | JUSTIFICATIONS |
|---|---|
|
||\begin{align} &\left(\dfrac{\color{blue}{36c^4d^6}}{\color{red}{e^8}} \right)^{\frac{-1}{2}} \\ =\ &\left(\dfrac{\color{red}{e^8}}{\color{blue}{36c^4d^6}}\right) ^{\frac{1}{2}} \end{align}|| |
Appliquer la loi qui met en relation un exposant négatif avec sa base : ||\left(\dfrac{\color{blue}{a}}{\color{red}{b}} \right) ^{-m} = \left(\dfrac{\color{red}{b}}{\color{blue}{a}} \right) ^m|| |
|
|= \dfrac{e^{\frac{8}{2}}}{36^{\frac{1}{2}}c^{\frac{4}{2}}d^{\frac{6}{2}}}| |
Distribuer l'exposant sur chacun des coefficients et des variables :||\left(\dfrac{a}{b}\right)^n = \dfrac{a^n}{b^n}|| |
|
|= \dfrac{e^4}{\color{red}{\sqrt{36}}c^2d^3}| |
Appliquer la loi des exposants fractionnaires : ||a^{\frac{m}{n}} = \sqrt[n]{a^m}|| |
|
Ainsi, l'égalité initiale est fausse puisque |\left( \dfrac{36c^4d^6}{e^8} \right)^{\frac{-1}{2}} = \dfrac{e^4}{6c^2d^3}| et non |\dfrac{e^4}{18c^2d^3}.| |
|
À voir aussi
Pour faire une mise en évidence simple, il s'agit de trouver un facteur commun à chacun des termes qui composent l'expression algébrique initiale. Une fois le facteur commun trouvé, on doit diviser l'expression algébrique par celui-ci et ajouter des parenthèses.
En tenant compte du dessin, détermine l'expression algébrique associée à la mesure de la longueur et à la mesure de la largeur.
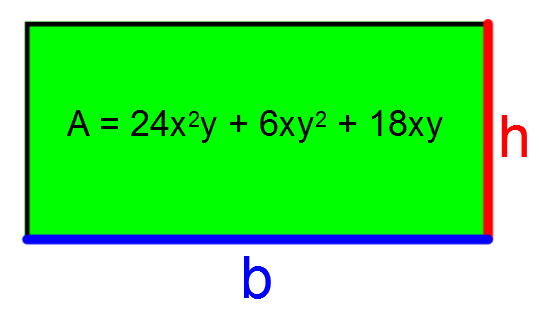
| CALCULS | JUSTIFICATIONS |
|---|---|
|
||\begin{align} 24x^2y \div 6xy &= 4x \\ 6xy^2 \div 6xy &= y \\ 18xy \div 6xy &= 3 \end{align}|| Ainsi, |6xy| est un facteur commun à chacun des termes. |
Trouver le plus grand facteur commun possible à chacun des termes. |
|
|24x^2y+6xy^2+18xy = \color{red}{6xy} (\color{blue}{4x +y+3})| |
Effectuer la mise en évidence. |
|
De façon arbitraire, on peut déterminer que l'expression algébrique associée la base du rectangle est |\color{blue}{4x + y + 3}| et celle de la hauteur est |\color{red}{6xy}.| |
|
À voir aussi
Pour résoudre une inéquation, on peut appliquer les mêmes principes de base que pour résoudre une équation. Par contre, il faut porter une attention particulière au symbole d'inéquation. Lorsqu'on divise ou qu'on multiplie par un nombre négatif, il faut inverser le signe d'inéquation : ||-4x \leq 12\ \Rightarrow\ x \geq -3||
Aujourd'hui, le double de mon âge additionné de trois équivaut à l'âge de mon frère. Quels sont les différents entiers qui peuvent être associés à mon âge si la somme de nos deux âges doit être inférieure à 60?
| CALCULS | JUSTIFICATIONS |
|---|---|
|
Mon âge |= \color{red}{x}| L'âge de mon frère | =\color{blue}{ 2x+3}| |
Identifier les variables et les inconnues. |
|
||\color{blue}{2x+3} + \color{red}{x} < 60|| |
Construire l'inéquation. |
|
||\begin{align} 3x + 3 &< 60 \\ 3x &< 57 \\ x &< 19 \end{align}|| |
Résoudre l'inéquation. |
|
Selon le contexte, on peut représenter cet ensemble-solution de trois façons différentes : Droite numérique
Extension |x \in \{0, 1, 2, 3, ..., 17, 18\}| Intervalle |0 \leq x < 19| avec |x \in \mathbb{N}| |
|
À voir aussi
Pour résoudre un système d'équations par comparaison, on peut se fier aux étapes suivantes :
-
Identifier les variables reliées aux inconnus.
-
Créer les équations selon la mise en situation.
-
Isoler la même variable pour chacune des équations.
-
Comparer les deux équations pour en former une nouvelle.
-
Résoudre cette nouvelle équation.
-
Remplacer la valeur de la variable dans une des équations de départ pour trouver la valeur de l'autre variable.
-
Répondre à la question posée.
Au dépanneur du coin, un groupe de travailleurs achète 4 cafés et 6 muffins pour 15,06 $. Le lendemain, ce même groupe se procure 3 cafés et 5 muffins pour une somme de 11,97 $. Si, le jour d'après, ces travailleurs veulent se procurer 6 cafés et 4 muffins, quelle somme devra être déboursée?
-
Identifier les inconnus à l'aide de variables.
|x:| cout pour un café ($)
|y:| cout pour un muffin ($)
-
Créer un système d'équations. ||\color{blue}{4x + 6y = 15{,}06} \\ \color{red}{3x + 5y = 11{,}97}||
-
Transformer chacune des équations sous la forme fonctionnelle. ||\begin{align} y &= \color{blue}{2{,}51 - \dfrac{4}{6}x} \\ y &= \color{red}{2{,}394 - \dfrac{3}{5}x} \end{align}||
-
Comparer les deux équations. ||\color{blue}{2{,}51 - \dfrac{4}{6}x} = \color{red}{2{,}394 -\dfrac{3}{5}x}||
-
Trouver la valeur de |x| en l'isolant avec les opérations inverses. ||\begin{align} \color{blue}{2{,}51 - \dfrac{4}{6}x} &= \color{red}{2{,}394 - \dfrac{3}{5}x} \\ 2{,}51 - 2{,}394 &= -\dfrac{3}{5}x + \dfrac{4}{6}x \\ 0{,}116 &= \dfrac{1}{15}x \\ 1{,}74 &= x \end{align}||
-
Substituer la valeur de |x| dans une des deux équations de départ pour trouver la valeur de |y|. ||\begin{align} 4\color{green}{x} + 6y &= 15{,}06 \\ 4 \color{green}{(1{,}74)} + 6y &= 15{,}06 \\ y &= 1{,}35 \end{align}||
-
Calculer le montant recherché selon 6 cafés et 4 muffins. ||\begin{align} 6 \ \text{cafés} + 4\ \text{muffins} &=\ ? \\ 6\color{green}{x} + 4\color{purple}{y} &=\ ? \\ 6 \color{green}{(1{,}74)} + 4 \color{purple}{(1{,}35)} &=\ ? \\ 15{,}84 &=\ ? \end{align}||
Réponse : La somme déboursée sera de |15{,}84\ $.|
À voir aussi
Pour chacun de ces termes, on peut leur associer une définition et une représentation graphique :
Relation : Pour une même valeur de |x,| il peut y avoir plus d'une valeur en |y.|
Fonction : Pour une même valeur de |x,| il existe au plus une valeur en |y.|
Réciproque : Notée |f^{-1}(x),| la réciproque d'une fonction consiste à inverser les variables dépendantes et indépendantes |\big((\color{blue}{x},\color{red}{y}) \mapsto (\color{red}{y}, \color{blue}{x})\big).|
À l'aide de la table des valeurs suivantes, détermine :
1) s'il s'agit d'une fonction ou d'une relation;
2) la table des valeurs qui définit sa réciproque.
| CALCULS | JUSTIFICATIONS |
|---|---|
|
1) Il s'agit d'une fonction. |
Pour chaque valeur en |x,| il existe au plus une valeur en |y.| |
|
2) La table des valeurs associées à la réciproque est : |
Il suffit d'inverser les valeurs de la variable dépendante et indépendante. |
À voir aussi
|\begin{align} f(x) &= ax + b \\\\ \text{où}\ a &= \dfrac{\Delta y}{\Delta x}= \dfrac{\color{red}{y_2}-\color{blue}{y_1}}{\color{red}{x_2}-\color{blue}{x_1}} \\ b &= \text{la valeur initiale} \end{align}|
|\color{blue}{(x_1, y_1)} , \color{red}{(x_2,y_2)}| sont des points situés sur la droite.
Afin d'estimer le temps nécessaire aux cyclistes pour terminer une étape, les dirigeants utilisent la vitesse moyenne de leur progression et en déduisent le graphique suivant :
À la lumière de ces informations, détermine la durée de cette course.
-
Calculer le taux de variation. ||\begin{align} a &= \dfrac{\color{red}{y_2} - \color{blue}{y_1}}{\color{red}{x_2}-\color{blue}{x_1}} \\ &= \dfrac{\color{red}{30{,}22} - \color{blue}{89}}{\color{red}{3{,}72}-\color{blue}{0}} \\ &= \dfrac{-58{,}78}{3{,}72} \\ &\approx -15{,}8 \end{align}||Ainsi, |f(x) = -15{,}8 x + b|
-
Trouver la valeur de |b| en substituant par un point situé sur la droite. ||\begin{align} \color{blue}{89} &= -15{,}8 \color{blue}{(0)} + b \\ \color{blue}{89} &= 0 + b \\ 89 &= b \end{align}||Ainsi, |f(x) = -15{,}8x + 89|
-
Remplacer |f(x)| par |0| étant donné le contexte. ||\begin{align} 0 &= -15{,}8x + 89 \\ -89 &= -15{,}8x \\ 5{,}63 &\approx x \end{align}||
Réponse : La course aura une durée d'environ |5{,}63| heures.
À voir aussi
|\begin{align} y &= \dfrac{k}{x} \\\\ k &= x y \end{align}|
Lors de la remise des lots des tirages hebdomadaires d'une loterie nationale, on sépare également le gros lot selon le nombre de gagnants. Voici une illustration de sa dernière répartition :
Selon ce contexte, détermine le montant gagné par chaque participant si on sait qu'il y a eu 5 gagnants?
-
Trouver la valeur de la constante |k.| ||\begin{align} k &= \color {blue}{x \times y} \\ k &= \color{blue}{2 \times 3} \\ &= 6 \end{align}||
-
Écrire l'équation de cette fonction de variation inverse. ||y=\dfrac{6}{x}||
-
Remplacer |x| par |\color{green}{5}.| ||\begin{align} y &= \dfrac{6}{\color{green}{5}} \\ y &= 1{,}2 \end{align}||
Réponse : Selon le contexte, chaque gagnant obtiendra la somme de 1,2 million de dollars.
À voir aussi
Il existe deux types de variables aléatoires |x| en probabilités :
-
Discrète : Lorsque |x \in \mathbb{N}|
-
Continue : Lorsque |x \in \mathbb{R}_+|
Dans chacune des situations, détermine s'il s'agit d'une variable discrète ou continue.
1) Détermine la probabilité en lien avec l'orientation, en degré, d'une aiguille qu'on laisse tomber sur le sol.
2) Détermine la probabilité en lien avec le résultat obtenu en lançant un dé à 6 faces.
1) Variable aléatoire continue.
Puisque l'orientation peut se donner selon un nombre qui fait partie des |\mathbb{R}_+| (ex: |45{,}6^\circ|), il s'agit d'une variable aléatoire continue.
2) Variable aléatoire discrète.
Puisque les résultats obtenus font partie de l'ensemble |\{1,2,3,4,5,6\}| et que chacun de ces résultats font partie des |\mathbb{N},| il s'agit d'une variable aléatoire discrète.
À voir aussi
|\mathbb{P} = \dfrac{\text{Aire de la région recherchée}}{\text{Aire de la région totale}}|
Pendant une foire, tu cherches à gagner un toutou de licorne pour garder un bon souvenir de ta soirée. Pour y arriver, tu dois atteindre une des zones rouges de la grande cible en lançant une balle.
Selon ces informations, quelle est la probabilité, en pourcentage, que tu partes avec un souvenir si tu lances la balle au hasard sachant que la base des triangles est équivalente au diamètre des cercles?
-
Trouver l'aire de la région recherchée. ||\begin{align} \color{red}{\text{Aire de la région recherchée}} &= \color{red}{A_\text{disque}} + \color{red}{A_\text{triangle}} \\ &= \pi (0{,}6 \div 2)^2 + \left(\dfrac{0{,}6 \times 0{,}85}{2}\right) \\ &\approx \color{red}{0{,}54 \ \text{m}^2} \end{align}||
-
Trouver l'aire de la région totale. ||\begin{align} \color{orange}{\text{Aire de la région totale}} &= b h \\ &= 2{,}5 \times 1{,}75 \\ &\approx \color{orange}{4{,}38 \ \text{m}^2} \end{align}||
-
Calculer la probabilité. ||\mathbb{P} = \dfrac{\color{red}{0{,}54}}{\color{orange}{4{,}38}} \approx 12{,}3\ \%||
Réponse : La probabilité de tirer au hasard sur une région rouge est d'environ |12{,}3\ \%.|
À voir aussi
|\mathbb{P} = \dfrac{\text{Nombre de résultats voulus}}{\text{Nombre total de résultats}}|
Une compagnie décide de mettre sur le marché des emballages de friandises qui sont composés de bonbons selon les couleurs primaires (bleu, rouge, jaune) et secondaires (vert, orange, mauve).
En prenant pour acquis que chaque emballage contient une friandise de chaque couleur, quelle est la probabilité que tu en achètes qui commence avec une friandise mauve et se termine avec une verte?
| CALCULS | JUSTIFICATIONS |
|---|---|
|
|\begin{align} \text{Nombre total de résultats} &= 6 \times 5 \times 4 \times 3 \times 2 \times 1 \\ &= 720 \end{align}| |
Utiliser la multiplication pour calculer le nombre de possibilités dans chaque emplacement. |
|
|\begin{align} \text{Nombre de résultats voulus} &= \color{purple}{1} \times 4 \times 3 \times 2 \times 1 \times \color{green}{1} \\ &= 24 \end{align}| |
Utiliser la multiplication pour calculer le nombre de possibilités dans chaque emplacement. |
|
|\mathbb{P} = \dfrac{24}{720} = \dfrac{1}{30}| |
Calculer la probabilité |
|
La probabilité d'acheter un emballage construit de la sorte est de |\dfrac{1}{30}.| |
|
À voir aussi
Voici une liste qui présente les méthodes d'échantillonnage les plus communes :
-
Aléatoire : Les éléments sont choisis au hasard, sans méthodologie précise.
-
Systématique : Les éléments sont choisis en respectant une fréquence précise.
-
Par grappes : Les éléments sont placés en sous-groupes, sans tenir compte d'aucune caractéristique précise, et les sous-groupes sont ensuite choisis au hasard.
-
Stratifié : Les éléments sont placés en sous-groupes selon une caractéristique précise (ex: âge, taille, poids, etc.).
Pour chacune des situations, identifie laquelle des méthodes est la plus appropriée.
1) Dans une usine, on contrôle la qualité en vérifiant un produit à chaque tranche de 100 qui sort de la chaine de production.
2) Pour essayer de prédire les résultats de la prochaine élection, on effectue un sondage sur les gens d'un même quartier.
3) Afin d'apporter des changements significatifs à leur prochain modèle de véhicule, un concessionnaire effectue un sondage auprès des gens âgés entre 30 et 40 ans.
| RÉPONSES | JUSTIFICATIONS |
|---|---|
|
1) Systématique |
Le contrôle de qualité s'effectue sur une fréquence régulière (1 à tous les 100 produits). |
|
2) Par grappes |
On a interrogé les gens qui font partie d'un même groupe formé selon aucune caractéristique précise. |
|
3) Stratifié |
Les gens sondés sont regroupés selon une caractéristique précise, leur âge. |
À voir aussi
||\text{Moyenne pondérée} = x_1 p_1 + x_2 p_2 +\dots + x_i p_i||où ||\begin{align} x_i &: \text{Résultat obtenu}\\ p_i &: \text{Pondération du résultat} \end{align}||
En te basant sur le tableau de distribution ci-dessus, calcule la moyenne pondérée.
||\begin{align} \text{Moyenne} &= \color{red}{60\ \% \times 20\ \%} + \color{blue}{65\ \% \times 10\ \%} + \color{green}{70\ \% \times 15\ \%} + 75\ \% \times 55\ \% \\ &= \color{red}{60\ \% \times 0{,}20} + \color{blue}{65\ \% \times 0{,}10} + \color{green}{70\ \% \times 0{,}15} + 75\ \% \times 0{,}55 \\&= 70{,}25\ \% \end{align}||
Réponse : La moyenne pondérée est de |70{,}25\ \%.|
À voir aussi
Dans ce type de tableau, les données sont regroupées en intervalles de même étendue. Pour effectuer les différents calculs de mesure de tendance centrale, on utilise la médiane de chacun des intervalles.
Afin de bien analyser les résultats des élèves de son groupe, un enseignant regroupe les données dans le tableau de distribution suivant :
Selon ces informations, détermine :
1) La classe modale
2) La classe médiane
3) La moyenne
| RÉPONSES | JUSTIFICATIONS |
|---|---|
|
1) Classe modale |= [70, 80[| |
C'est la classe qui a le plus grand effectif. |
|
2) Classe médiane |=[70, 80[| |
Puisqu'il y a un total de 23 données, on choisit la classe qui contient la |12^{\text{e}}| donnée. |
|
|\begin{align} 3)\ \text{Moyenne} &\approx \dfrac{\color{red}{\left( \frac{40+50}{2} \times 2 \right)} + \color{blue}{\left( \frac{50+60}{2}\times 3 \right) } + \dots + \color{green}{\left( \frac{90+100}{2} \times 2\right)}}{23} \\ &\approx 70{,}65 \end{align}| |
On applique le calcul usuel de la moyenne, mais en considérant la médiane de chacune des classes. |
À voir aussi
|Q_1 =| 1er quartile |=| Médiane de la première moitié de la distribution
|Q_2=| 2e quartile |=| Médiane de toute la distribution
|Q_3 =| 3e quartile |=| Médiane de la deuxième moitié de la distribution
|Q_3 - Q_1=| Étendue interquartile
De par ses critères de construction, chaque section du diagramme de quartiles comporte environ 25 % des données de la distribution.
À l'aide du diagramme de quartiles suivant, détermine si les énoncés sont vrais ou faux en justifiant chacune de tes réponses.
1) Environ |50\ \%| des données sont incluses entre |\color{green}{25}| et |\color{orange}{55}.|
2) L'étendue interquartile est de |65.|
3) Il y a plus de données entre |\color{green}{25}| et |\color{red}{45}| qu'entre |\color{red}{45}| et |\color{orange}{55}.|
4) La moyenne de la distribution est |\color{red}{45}.|
| RÉPONSES | JUSTIFICATIONS |
|---|---|
|
1) Vrai |
Chaque section contient environ |25\ \%| des données. Donc, 2 sections |\approx 50\ \%| des données. |
|
2) Faux |
L'étendue interquartile |= Q_3 - Q_1 = \color{orange}{55}-\color{green}{25} = 30|. |
|
3) Faux |
Chaque section contient environ |25\ \%| des données. Même si le rectangle est plus long, cela ne signifie pas qu'il y a plus de données, cela signifie plutôt qu'elles sont plus dispersées. |
|
4) Faux |
La médiane est de |\color{red}{45}.| Il est impossible de calculer précisément la moyenne avec ce genre de diagramme. |
À voir aussi
Pour construire un nuage de points, il suffit de placer chacun des couples d'une même situation dans un plan cartésien en les identifiant avec un point.
Afin d'avoir une meilleure représentation de la progression de la performance de ses joueurs, un entraineur de hockey analyse le nombre de parties jouées et le nombre de points obtenus selon les trois dernières saisons.
Pour l'aider à synthétiser le tout, construis un nuage de points avec toutes ces données.
1) Identifier les axes et le titre.
2) Créer une légende pour chacune des saisons.
|\color{red}{\bullet}:| Saison 2013-2014
|\color{blue}{\bullet}:| Saison 2014-2015
3) Placer chacune des coordonnées dans le plan cartésien.
À voir aussi
| Projections orthogonales (différentes vues) | |
|---|---|
| Projections parallèles | |
|
Perspective cavalière (seule la face frontale n'est pas déformée) |
Perspective axonométrique (mesures d'arêtes proportionnelles à la réalité) |
| |
|
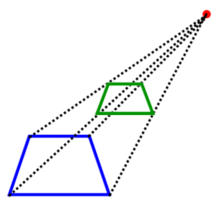
| Projections centrales | |
| Perspective à un point de fuite | Perspective à deux points de fuite |
 |
|
En te fiant aux différentes vues d'une projection orthogonale présentées plus haut, lequel des solides suivants peut y être associé ?
| DÉDUCTIONS | JUSTIFICATIONS |
|---|---|
|
1) Ce ne sont pas A et B. |
La vue de gauche n'est pas adéquate. |
|
2) Ce n'est pas C. |
La vue de face n'est pas adéquate. |
|
Le solide associé aux vues présentées est le solide D. |
|
À voir aussi
-
|\text{Rapport de similitude} = \dfrac{\text{Dimension de la figure image}}{\text{Dimension correspondante de la figure initiale}}=k^1|
-
|\text{Rapport d'aires} = \dfrac{\text{Aire de la figure image}}{\text{Aire de la figure initiale}}=k^2|
-
|\text{Rapport de volumes} = \dfrac{\text{Volume du solide image}}{\text{Volume du solide initial}}=k^3|
Voici les liens arithmétiques qui existent entre chacun des rapports :
Pour s'assurer que chaque client soit satisfait, une compagnie vend des chapeaux de fête de deux dimensions : une pour les adultes et une pour les enfants. La hauteur du modèle pour adulte mesure 7 cm de plus que celle du modèle pour enfant.
En sachant que le rapport de leurs aires latérales respectives est de |\dfrac{49}{25},| quelle est la hauteur de chacun des chapeaux?
1) Calculer la valeur de |k^1.| ||\begin{align} k^1 &= \sqrt{k^2} \\ &= \sqrt{\dfrac{49}{25}} \\ &= \dfrac{7}{5} \end{align}||
2) Établir la proportion selon le rapport |k^1| trouvé. ||\dfrac{\color{red}{h+7}}{\color{blue}{h}} = \dfrac{7}{5}||
3) Résoudre l'équation. ||\begin{align} 5 \color{red}{(h+7)} &= 7 \color{blue}{h} \\ 5h + 35 &= 7h \\ 35 &= 2h \\ 17{,}5 &= h \end{align}||
Réponse : Le modèle pour enfant a une hauteur de |\color{blue}{h} = 17{,}5\ \text{cm}| et le modèle pour adulte a une hauteur de |\color{red}{h+7} = 17{,}5 \color{red}{+7} = 24{,}5\ \text{cm}.|
À voir aussi
Puisqu'il est question d'un solide décomposable, il sera préférable de travailler avec l'aire de chacune des faces du solide plutôt que l'aire totale de chacun des solides qui le composent. En d'autres mots, les formules d'aires des figures planes seront à privilégier.
|
|A_\text{carré} = c^2| |
|A_\text{rectangle} = b\times h| |
|A_\text{losange} = \displaystyle \frac{D \times d}{2}| |
|
|A_\text{parallélogramme}=b \times h| |
|A_\text{trapèze} = \displaystyle \frac{(B+b)\times h}{2}| |
|A_\text{triangle} = \displaystyle \frac{b \times h}{2}| |
|
|A_\text{disque}=\pi r^2| |
|A_\text{polygone régulier}= \displaystyle \frac{c a n}{2}| |
|A_\text{cône}= \pi r^2 + \pi r a| |
|
|A_\text{cylindre}=2\pi r^2 + 2\pi r h| |
||
Une fois arrivé dans un magasin d'antiquité, un collectionneur aperçoit ce coffre. S'il l'achète, il aura besoin de connaitre la hauteur totale de ce dernier puisqu'il doit être semblable à ceux qu'il possède déjà. Pour des fins de restauration, l'aire totale est connue.
Quelle est la hauteur de ce coffre?
1) Identifier la mesure manquante.
2) Créer l'équation en lien avec le calcul de l'aire totale. ||\begin{align} A_\text{totale} &= A_\text{base}+2 A_\text{faces gauche-droite}+2 A_\text{faces avant-arrière}+\dfrac{1}{2} A_\text{L cylindre}+A_\text{disque} \\ 7{,}15 &= \color{red}{1{,}35}\times \color{fuchsia}{0{,}9} + 2 (\color{fuchsia}{0{,}9}\times \color{blue}{h}) + 2 (\color{red}{1{,}35}\times \color{blue}{h}) + \frac{1}{2}(2 \pi \times \color{fuchsia}{0{,}45} \times \color{red}{1{,}35}) + \pi\times \color{fuchsia}{0{,}45}^2 \end{align}||
3) Résoudre en trouvant la valeur de |\color{blue}{h}.| ||\begin{align} 7{,}15 &\approx 1{,}215 + 1{,}8\color{blue}{h} + 2{,}7\color{blue}{h} + 1{,}908+0{,}636 \\ 7{,}15 &\approx 3{,}759 + 4{,}5\color{blue}{h} \\ 3{,}391 &\approx 4{,}5\color{blue}{h} \\ 0{,}75 &\approx \color{blue}{h} \end{align}||
Réponse : La hauteur totale du coffre | \approx \color{blue}{h} + \color{fuchsia}{0{,}45} \approx \color{blue}{0{,}75}+\color{fuchsia}{0{,}45} \approx 1{,}2 \ \text{m}.|
À voir aussi
Unités de longueur
Unités d'aire
Unités de volume
Unités de capacité
Volume et capacité
| |1 \ \text{kL} = 1 \ \text{m}^3| | |1 \ \text{L} = 1 \ \text{dm}^3| | | 1 \ \text{mL} = 1 \ \text{cm}^3| |
Il y a quelques années, une municipalité offrait ses services afin d'aider les gens à remplir leur piscine. Afin d'éviter les abus, elle fournissait gratuitement l'aide des pompiers pour les premiers |\color{blue}{5 \ 000}\ \text{L}| d'eau. Pour le reste, elle chargeait un supplément de |0{,}002\ $| par litre supplémentaire.
Quelle somme devrait être déboursée pour remplir une piscine d'un volume de |\color{red}{22 \ \text{m}^3}|?
-
Transformer toutes les données sous la même unité. ||\begin{align} \color{red}{22 \ \text{m}^3} &= 22\ \text{kL} \\ &= 22 \ 000 \ \text{L} \end{align}||
-
Déterminer le quantité d'eau à payer. ||\begin{align} \text{Eau à payer} &= 22 \ 000 - \color{blue}{5 \ 000} \\ &= 17 \ 000\ \text{L} \end{align}||
Réponse : Le cout |= 17 \ 000 \times 0{,}002 = 34\ \$.|
À voir aussi
Pour être en mesure de calculer le volume des solides décomposables, il est important de garder en mémoire les formules de volume de solides.
|
|V_\text{prisme} = A_b \times h| |
|V_\text{cube} = c^3| |
|V_\text{pyramide} = \displaystyle \frac{A_b \times h}{3}| |
|
|V_\text{cylindre} = \pi r^2 \times h| |
|V_\text{boule} = \displaystyle \frac{4 \pi r^3}{3}| |
|V_\text{cône} = \displaystyle \frac{\pi r^2 \times h}{3}| |
Après avoir fait plusieurs achats dans ta boutique de meubles préférée, tu utilises ta remorque personnelle afin de tout transporter. Dû à certaines réglementations, ton chargement ne doit pas dépasser 3 m de hauteur à partir du sol.
À la lumière des informations que tu as, détermine si ton chargement est conforme ou non en sachant que ta remorque est d'une largeur de |\color{blue}{1{,}5}\ \text{m}.|
-
Identifier la règle à utiliser pour le volume du demi-cylindre. ||V = \dfrac{\pi r^2 \times\color{blue}{h}}{2}||
-
Remplacer les valeurs connues et isoler la variable restante |r.| ||\begin{align} \color{orange}{1{,}75} &= \dfrac{\pi r^2 \times \color{blue}{1{,}5}}{2} \\ 3{,}5 &= 1{,}5 \pi r^2 \\ 0{,}74 &\approx r^2 \\ 0{,}86 &\approx r \end{align}||
Réponse : Puisque la hauteur totale du chargement |= 0{,}45 + \color{fuchsia}{1{,}55}+\color{green}{0{,}35} + \color{orange}{0{,}86} = 3{,}21\ \text{m},| cela signifie que ton chargement n'est pas conforme, car |3{,}21 > 3.|
À voir aussi
|\color{blue}{a}^2 + \color{red}{b}^2 = \color{green}{c}^2|
où
|\color{blue}{a}| et |\color{red}{b} = | mesures des cathètes
|\color{green}{c} = | mesure de l'hypoténuse
Pour sauver les gens d'un incendie, les pompiers veulent installer un pont temporaire pour permettre aux gens de passer de l'édifice en feu à un édifice sécuritaire.
A la lumière des informations fournies sur le dessin, quelle doit être la longueur minimale du pont?
-
Identifier le triangle rectangle et ses mesures. ||\begin{align} \color{blue}{\text{Cathète}_1} &=\color{blue}{a}= 15 - 13{,}25 = 1{,}75\ \text{m} \\ \color{red}{\text{Cathète}_2} &=\color{red}{b} = 9{,}75\ \text{m} \\ \color{green}{\text{Hypoténuse}} &= \color{green}{c} =\ ? \end{align}||
-
Appliquer la relation de Pythagore. ||\begin{align} \color{blue}{a}^2 +\color{red}{b}^2 &= \color{green}{c}^2 \\ \color{blue}{1{,}75}^2 + \color{red}{9{,}75}^2 &= \color{green}{c}^2 \\98{,}125 &= \color{green}{c}^2 \\ 9{,}91 &\approx \color{green}{c} \end{align}||
Réponse : Le pont devra être d'une longueur minimale de |9{,}91\ \text{m}.|
