Here is a short preparation guide containing all the concepts covered in Secondary 3. To explain everything, each formula will be followed by an example and a link that leads to a concept sheet in our virtual library.
In this section, it is important to differentiate between the following sets:
|\mathbb{N} = | Natural numbers: Positive whole numbers.
|\mathbb{Z} = | Integers: Positive and negative whole numbers.
|\mathbb{Q} = | Rational numbers: Numbers that can be written as a fraction in the form |\frac{a}{b}| with |\{a, b\} \in \mathbb{Z}| and |b \neq 0.|
|\mathbb{Q}' = | Irrational numbers: Numbers that cannot be written as a fraction of the form |\frac{a}{b}| with |\{a,b\} \in \mathbb{Z}| and |b \neq 0.|
|\mathbb{R} = | Real numbers: Set of numbers that includes all the sets presented above.
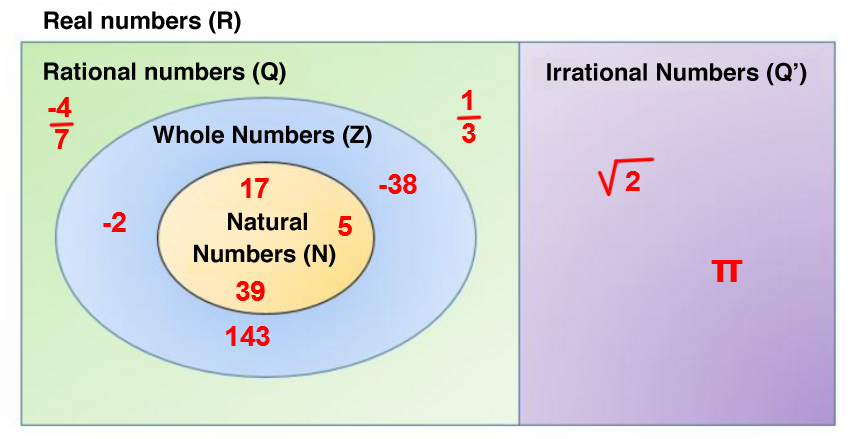
We can also use the signs “*”, “+”, and “-” to refer to a set that does not contain the number 0, strictly positive numbers, or strictly negative numbers (e.g., |\mathbb{N} = \mathbb{Z}_+| ) .
What is the smallest number set that includes the following numbers: ||\{0{.}125\,\ 19\ \%\,\ 0{.}\overline{666}\,\ 30\}||
|
CALCULATIONS |
JUSTIFICATIONS |
|---|---|
|
||\begin{align} 0{.}125 &= \dfrac{125}{1000} = \dfrac{1}{8} \\ 19\ \% &= \dfrac{19}{100}\\ 0{.}\overline{666} &= \dfrac{2}{3} \end{align}|| |
|\{0{.}125 , 19\ \%, 0{.}\overline{666}\} \in \mathbb{Q},| because we can write them all as a fraction |\dfrac{a}{b}| with |\{a,b\} \in \mathbb{Z}.| |
|
|30| |
|30 \in \mathbb{N},| because it is a positive integer. |
|
Due to the fact all of the numbers are positive and the |0| is not mentioned, we can say the smallest number set grouping them together is |\mathbb{Q}^*_+.| |
|
See also
When subsets are written, it is important to respect the different notation conventions, as follows:
Intervals: Use square brackets to indicate the start and end of the subset.
List/Roster: Use set brackets to enumerate or list all numbers from the start to the end of the subset. If it is infinite, you can use an ellipsis (...).
Number line: Use a number line to represent the start and end of the subset.
Use all three notation methods to represent the following subset: ||-3 < x \leq 2{.}5||
|
CALCULATIONS |
JUSTIFICATIONS |
|---|---|
|
Intervals ||x \in\ ]-3;\ 2{.}5]|| |
Since |-3| is excluded, an open bracket is used |(\ ]\ )| and to identify that the |2{.}5| is included, a closed bracket is used |(\ ]\ ).| |
|
Number line |
When drawing a number line, we use the closed point |(\bullet)| for numbers that are included and an open point for numbers that are excluded |(\circ).| |
|
In this case, it is impossible to use extension notation, because it is impossible to write all the numbers that exist between |-3| and |2{.}5.| |
|
See also
To write a number in scientific notation, we use the notation |a \times 10^b| with |1\leq a <10| and |b \in \mathbb{Z}.|
Addition and subtraction
- Ensure that the value of |b| is the same for each term.
- Perform the operation on the coefficients |a.|
- If necessary, modify the exponent |b| so that |1 \leq a <10.|
Multiplication and division
- Perform the operation on the coefficients |a.|
- Apply the laws of exponents to the exponent |b.|
- If necessary, modify the final value of |b| to ensure |1 \leq a < 10.|
Using scientific notation, what is the result of the following chain of operations: ||(2{.}1 \times 10^5 + 4{.}2 \times 10^4) \times 8{.}43 \times 10^{12}||
|
CALCULATIONS |
JUSTIFICATIONS |
|---|---|
|
||\begin{align} &(\color{red}{2{.}1 \times 10^5} + 4{.}2 \times 10^4) \times 8{.}43 \times 10^{12} \\ =\ &(\color{red}{21 \times 10^4} + 4{.}2 \times 10^4) \times 8{.}43 \times 10^{12} \\ =\ &\color{blue}{25{.}2} \times 10\color{green}{^4} \times \color{blue}{8{.}43} \times 10\color{green}{^{12}} \end{align}|| |
Modify the terms that can be added so their exponent has the same value. |
|
||\begin{align} |
Multiply the coefficients and apply the appropriate exponent law. |
|
||=2{.}124 \ 36 \times 10^{18}|| |
Modify the value of the exponent so the coefficient is |\in [1,10[.| |
|
The result is |2{.}124 \ 36 \times 10^{18}.| |
|
See also
To simplify an exponential expression, remember the laws of exponents:
|
|\left(\dfrac{a}{b}\right)^{-m} = \left(\dfrac{b}{a}\right)^m| |
|(ab)^m = a^m b^m| |
|
|a^{\frac{m}{n}} = \sqrt[n]{a^m}| |
|\left(\dfrac{a}{b}\right)^m = \dfrac{a^m}{b^m}| |
|
|a^m \times a^n = a ^{m+n}| |
|(a^m)^n = a^{m n}| |
|
|\dfrac{a^m}{a^n} = a^{m-n}| |
|a^0=1| |
Determine whether the following two exponential expressions are equal: ||\left(\dfrac{36c^4d^6}{e^8} \right)^{\frac{-1}{2}} = \dfrac{e^4}{18c^2d^3}||
|
CALCULATIONS |
JUSTIFICATIONS |
|---|---|
|
||\begin{align} &\left(\dfrac{\color{blue}{36c^4d^6}}{\color{red}{e^8}} \right)^{\frac{-1}{2}} \\ =\ &\left(\dfrac{\color{red}{e^8}}{\color{blue}{36c^4d^6}}\right) ^{\frac{1}{2}} \end{align}|| |
Apply the law that relates a negative exponent to its base: |
|
|= \dfrac{e^{\frac{8}{2}}}{36^{\frac{1}{2}}c^{\frac{4}{2}}d^{\frac{6}{2}}}| |
Distribute the exponent over each of the coefficients and variables: ||\left(\dfrac{a}{b}\right)^n = \dfrac{a^n}{b^n}|| |
|
|= \dfrac{e^4}{\color{red}{\sqrt{36}}c^2d^3}| |
Apply the law of fractional exponents: ||a^{\frac{m}{n}} = \sqrt[n]{a^m}|| |
|
Thus, the initial equality is false because |\left( \dfrac{36c^4d^6}{e^8} \right)^{\frac{-1}{2}} = \dfrac{e^4}{6c^2d^3}| and not |\dfrac{e^4}{18c^2d^3}.| |
|
See also
To factor out the Greatest Common Factor (GCF), locate a factor common to each of the terms that make up the initial algebraic expression. Once the common factor has been found, divide the algebraic expression by it and add brackets.
Study the following diagram and determine the algebraic expression associated with the base and height.
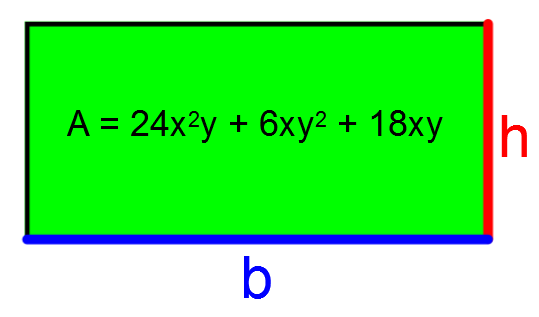
|
CALCULATIONS |
JUSTIFICATIONS |
|---|---|
|
||\begin{align} 24x^2y \div 6xy &= 4x \\ 6xy^2 \div 6xy &= y \\ 18xy \div 6xy &= 3 \end{align}|| |
Find the GCF for each term. |
|
|24x^2y+6xy^2+18xy = \color{red}{6xy} (\color{blue}{4x +y+3})| |
Factor out the GCF. |
|
Arbitrarily, we can determine that the algebraic expression associated with the rectangle’s base is |\color{blue}{4x + y + 3}| and the height is |\color{red}{6xy}.| |
|
See also
To solve an inequality, the same basic principles can be used as for solving an equation. However, special attention must be paid to the inequality symbol. When dividing or multiplying by a negative number, the direction of inequality sign must be reversed: ||-4x \leq 12\ \Rightarrow\ x \geq -3||
At the moment, if I double my age and add three it is equal to my brother's age. What are the different integers associated with my age if the sum of our two ages is less than 60?
|
CALCULATIONS |
JUSTIFICATIONS |
|---|---|
|
My age |= \color{red}{x}| |
Identify the variables and the unknowns. |
|
||\color{blue}{2x+3} + \color{red}{x} < 60|| |
Build the inequality. |
|
||\begin{align} 3x + 3 &< 60 \\ 3x &< 57 \\ x &< 19 \end{align}|| |
Solve the inequality. |
|
Depending on the context, we can represent this solution set in three different ways: Number Line
List/Roster |x \in \{0, 1, 2, 3, ..., 17, 18\}| Interval |0 \leq x < 19| with |x \in \mathbb{N}| |
|
See also
To solve a system of equations by comparison, follow these steps:
-
Identify the variables related to the unknowns.
-
Create a system of equations according to the scenario.
-
Isolate the same variable for each equation.
-
Compare the two equations to form a new one.
-
Solve the new equation.
-
Substitute the value of the found variable in one of the starting equations to find the value of the other variable.
-
Answer the question.
At the corner store, a group of workers bought 4 coffees and 6 muffins for $15.06. The next day, the same group bought 3 coffees and 5 muffins for a sum of $11.97. On the following day, how much will the workers pay if they want to buy 6 coffees and 4 muffins?
-
Identify unknowns using variables.
|x:| cost of a coffee ($)
|y:| cost of a muffin ($) -
Create a system of equations.||\color{blue}{4x + 6y = 15{.}06} \\ \color{red}{3x + 5y = 11{.}97}||
-
Convert each of the equations into their functional form. ||\begin{align} y &= \color{blue}{2{.}51 - \dfrac{4}{6}x} \\ y &= \color{red}{2{.}394 - \dfrac{3}{5}x} \end{align}||
-
Compare the two equations. ||\color{blue}{2{.}51 - \dfrac{4}{6}x} = \color{red}{2{.}394 -\dfrac{3}{5}x}||
-
Find the value of |x| isolating it using the reverse order of operations. ||\begin{align} \color{blue}{2{.}51 - \dfrac{4}{6}x} &= \color{red}{2{.}394 - \dfrac{3}{5}x} \\ 2{.}51 - 2{.}394 &= -\dfrac{3}{5}x + \dfrac{4}{6}x \\ 0{.}116 &= \dfrac{1}{15}x \\ 1{.}74 &= x \end{align}||
-
Substitute the value of |x| into one of the two starting equations to find the value of |y| .||\begin{align} 4\color{green}{x} + 6y &= 15{.}06 \\ 4 \color{green}{(1{.}74)} + 6y &= 15{.}06 \\ y &= 1{.}35 \end{align}||
-
Calculate the amount based on 6 coffees and 4 muffins. ||\begin{align} 6 \ \text{coffees} + 4\ \text{muffins} &=\ ? \\ 6\color{green}{x} + 4\color{purple}{y} &=\ ? \\ 6 \color{green}{(1{.}74)} + 4 \color{purple}{(1{.}35)} &=\ ? \\ 15{.}84 &=\ ? \end{align}||
Answer: They will need to pay |$15{.}84.|
See also
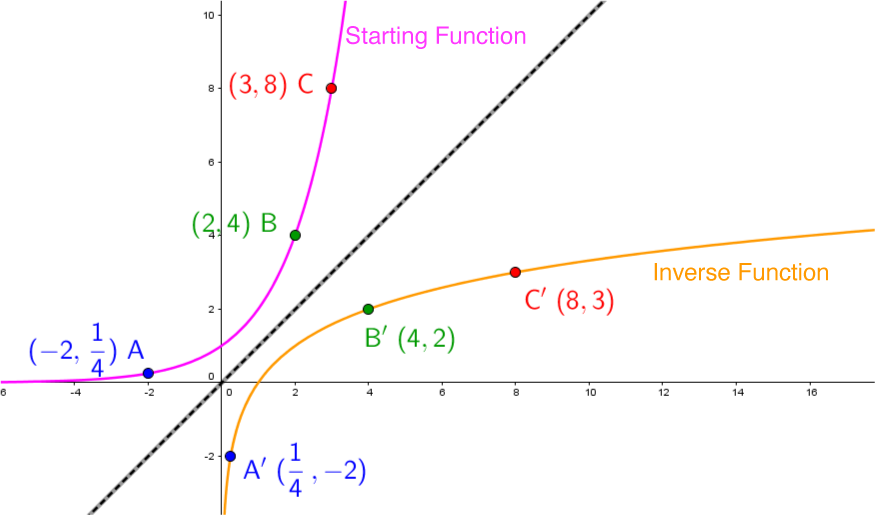
Each term is associated with a definition and a graphical representation:
Relation: For the same value of |x,| there may be more than one value of |y.|
Function: For the same value of |x,| there is at most one value of |y.|
Inverse: Written |f^{-1}(x),| the inverse of a function consists of inverting the dependent and independent variables |\big((\color{blue}{x},\color{red}{y}) \mapsto (\color{red}{y}, \color{blue}{x})\big).|
Using the following table of values, determine:
1) If it is a function or a relation.
2) The table of values which defines its inverse.
|
CALCULATIONS |
JUSTIFICATIONS |
|---|---|
|
1) It is a function. |
For each value of |x,| there is at most one value of |y.| |
|
2) The table of values associated with the inverse is the following: |
It suffices to switch the values of the dependent and independent variable. |
See also
|\begin{align} f(x) &= ax + b \\\\ \text{where}\ a &= \dfrac{\Delta y}{\Delta x}= \dfrac{\color{red}{y_2}-\color{blue}{y_1}}{\color{red}{x_2}-\color{blue}{x_1}} \\ b &= \text{the initial value} \end{align}|
|\color{blue}{(x_1, y_1)}, \color{red}{(x_2,y_2)}| are points on the right.
To estimate the time necessary for cyclists to complete a stage, the leaders use the average speed of their progress and plot the following graph:
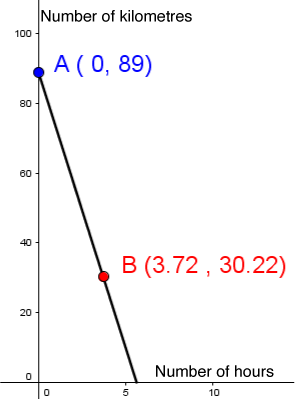
Determine the duration of the race using the information on the graph.
-
Calculate the rate of change. ||\begin{align} a &= \dfrac{\color{red}{y_2} - \color{blue}{y_1}}{\color{red}{x_2}-\color{blue}{x_1}} \\ &= \dfrac{\color{red}{30{.}22} - \color{blue}{89}}{\color{red}{3{.}72}-\color{blue}{0}} \\ &= \dfrac{-58{.}78}{3{.}72} \\ &\approx -15{.}8 \end{align}|| Thus, |f(x) = -15{.}8 x + b|
-
Find the value of |b| by substituting it with a point on the right. ||\begin{align} \color{blue}{89} &= -15{.}8 \color{blue}{(0)} + b \\ \color{blue}{89} &= 0 + b \\ 89 &= b \end{align}|| Thus, |f(x) = -15{.}8x + 89|
-
Replace |f(x)| by |0| given the context. ||\begin{align} 0 &= -15{.}8x + 89 \\ -89 &= -15{.}8x \\ 5{.}63 &\approx x \end{align}||
Answer: The race will last approximately |5{.}63| hours.
See also
|\begin{align} y &= \dfrac{k}{x} \\\\ k &= x y \end{align}|
When awarding prizes for the weekly draw of a national lottery, the jackpot is equally divided amongst the number of winners. The following is an illustration of the latest payout:
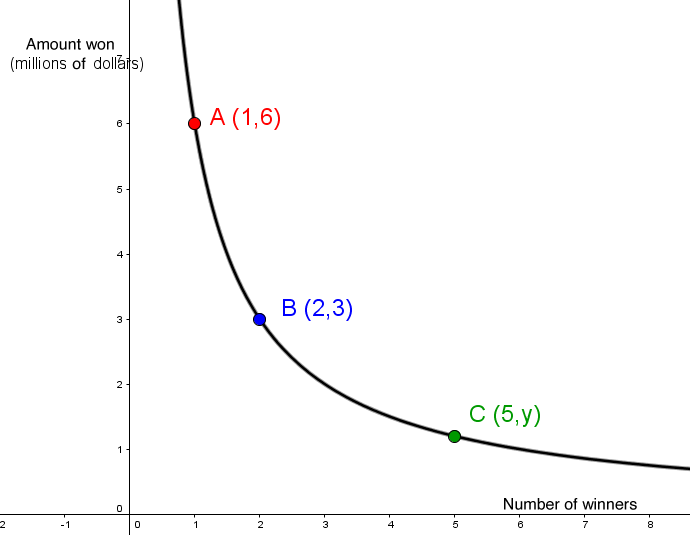
Based on this context, how much did each participant win if there were 5 winners?
-
Find the value of the constant |k|. ||\begin{align} k &= \color {blue}{x \times y} \\ k &= \color{blue}{2 \times 3} \\ &= 6 \end{align}||
-
Write the equation of the inverse variation function.||y=\dfrac{6}{x}||
-
Replace |x| with |\color{green}{5}.| ||\begin{align} y &= \dfrac{6}{\color{green}{5}} \\ y &= 1{.}2 \end{align}||
Answer: According to the context of this situation, each winner will get $1.2 million.
See also
There are two types of random variables |x| in probability:
-
Discrete: When |x \in \mathbb{N}|
-
Continuous: When |x \in \mathbb{R}_+|
In each situation, determine whether the variable is discrete or continuous.
-
Determine the probability based on the orientation (in degrees) of a pointer that is dropped on the ground.
-
Determine the probability based on the results of throwing a 6-sided die.
-
Continuous random variable.
Since the orientation can be given according to a number which is part of the |\mathbb{R}_+| (e.g., |45{.}6^\circ| ), it is a continuous random variable. -
Discrete random variable.
Since the results are part of the set |\{1,2,3,4,5,6\}| and each result is part of the |\mathbb{N},| it is a discrete random variable.
See also
|\mathbb{P} = \dfrac{\text{Area of the desired region}}{\text{Area of the total region}}|
You want to win a unicorn toy as a souvenir of your evening at the fair. To win, you have to throw a ball and hit one of the large target’s red areas.
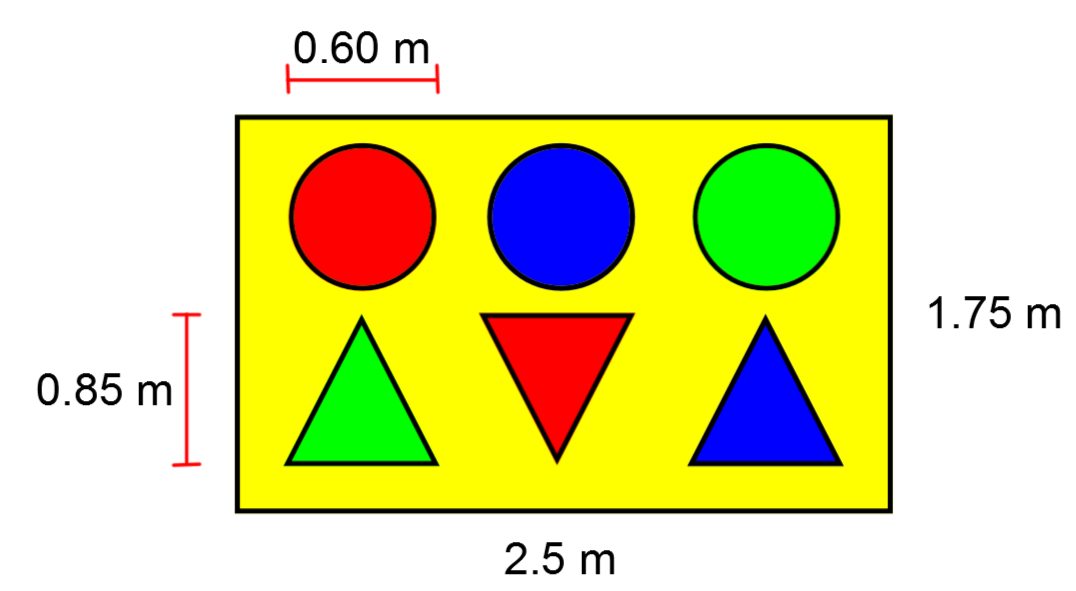
Based on those informations, what is the probability (as a percentage) that you leave with a unicorn toy if you throw the ball at random, givent that the measure of the triangles' bases are equivalent to the circles' diameter?
-
Find the area of the desired region. ||\begin{align} \color{red}{\text{Area of the desired region}} &= \color{red}{A_\text{disc}} + \color{red}{A_\text{triangle}} \\ &= \pi (0{.}6 \div 2)^2 + \left(\dfrac{0{.}6 \times 0{.}85}{2}\right) \\ &\approx \color{red}{0{.}54 \ \text{m}^2} \end{align}||
-
Find the area of the total region. ||\begin{align} \color{orange}{\text{Area of the total region}} &= b h \\ &= 2{.}5 \times 1{.}75 \\ &\approx \color{orange}{4{.}38 \ \text{m}^2} \end{align}||
-
Calculate the probability. ||\mathbb{P} = \dfrac{\color{red}{0{.}54}}{\color{orange}{4{.}38}} \approx 12{.}3\ \%||
Answer: The probability of randomly hitting a red region is approximately |12{.}3\ \%.|
See also
|\mathbb{P} = \dfrac{\text{Number of desired results}}{\text{Total number of results}}|
A company decides to market candy whose packaging consists of candy in the primary (blue, red, yellow) and secondary (green, orange, purple) colours.
Assuming each package contains one candy of each color, what is the probability that you will start by eating a purple one and finish by eating a green one?
|
CALCULATIONS |
JUSTIFICATIONS |
|---|---|
|
|\begin{align} \text{Total number of results} &= 6 \times 5 \times 4 \times 3 \times 2 \times 1 \\ &= 720 \end{align}| |
Use multiplication to calculate the number of possibilities in each position. |
|
|\begin{align} \text{Number of desired results} &= \color{purple}{1} \times 4 \times 3 \times 2 \times 1 \times \color{green}{1} \\ &= 24 \end{align}| |
Use multiplication to calculate the number of possibilities in each position. |
|
|\mathbb{P} = \dfrac{24}{720} = \dfrac{1}{30}| |
Calculate the probability |
|
The probability of purchasing a bag of candy sorted this way is |\dfrac{1}{30}.| |
|
See also
The following are the most common sampling methods:
-
Random: The elements are chosen at random, without precise methodology.
-
Systematic: The elements are chosen respecting a precise frequency.
-
Cluster: The elements are placed in subgroups without considering any specific characteristics, and the subgroups are then chosen at random.
-
Stratified: The elements are placed in subgroups according to a specific characteristic (e.g., age, height, weight, and so on).
Identify which method is the most appropriate for each situation.
1) We conduct quality control in a factory by checking 1 out of every 100 products that leave the production line.
2) We conduct a survey of people in the same neighborhood to try to predict the results of the next election.
3) A dealership surveys people between the ages of 30 and 40 to make significant changes to their next vehicle model.
|
ANSWERS |
JUSTIFICATIONS |
|---|---|
|
1) Systematic |
Quality control is carried out on a regular basis (1 out of every 100 products). |
|
2) Cluster |
We interviewed people who are part of the same group, formed according to no specific characteristics. |
|
3) Stratified |
The people surveyed are grouped according to a specific characteristic (i.e., by age). |
See also
||\text{Weighted mean} = x_1 p_1 + x_2 p_2 +\dots + x_i p_i|| where ||\begin{align} x_i &: \text{Result}\\ p_i &: \text{weight of result} \end{align}||
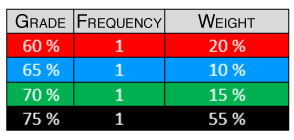
Based on the distribution table above, calculate the weighted mean.
||\begin{align} \text{Mean} &= \color{red}{60\ \% \times 20\ \%} + \color{blue}{65\ \% \times 10\ \%} + \color{green}{70\ \% \times 15\ \%} + 75\ \% \times 55\ \% \\ &= \color{red}{60\ \% \times 0{.}20} + \color{blue}{65\ \% \times 0{.}10} + \color{green}{70\ \% \times 0{.}15} + 75\ \% \times 0{.}55 \\&= 70{.}25\ \% \end{align}||
Answer: The weighted mean is |70{.}25\ \%.|
See also
In this type of table, the data is grouped into intervals of the same range. The median of each interval is used to perform the various measures of central tendency calculations.
To properly analyze the student results in groups, a teacher sorts the data in the following distribution table:
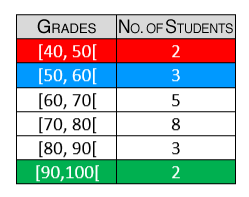
Based on the information, the teacher determines the following:
1) The modal class
2) The medial class
3) The mean
|
ANSWERS |
JUSTIFICATIONS |
|---|---|
|
1) Modal class |= [70, 80[| |
The class that has the largest number of students. |
|
2) Medial class |=[70, 80[| |
Since there is a total of 23 data points, we choose the class containing the |12^{\text{th}}| . |
|
|\begin{align} 3)\ \text{ Mean} &\approx \dfrac{\color{red}{\left( \frac{40+50}{2} \times 2 \right)} + \color{blue}{\left( \frac{50+60}{2}\times 3 \right) } + \dots + \color{green}{\left( \frac{90+100}{2} \times 2\right)}}{23} \\ &\approx 70{.}65 \end{align}| |
The usual calculation of the mean is applied, but considering the median of each class. |
See also
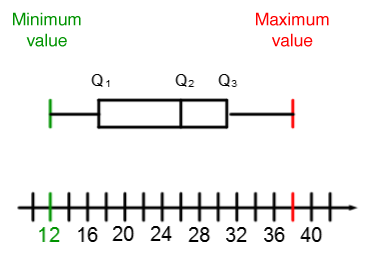
|Q_1 =| 1st quartile |=| Median of the first half of the distribution
|Q_2=| 2nd quartile |=| Median of the entire distribution
|Q_3 =| 3rd quartile |=| Median of the second half of the distribution
|Q_3 - Q_1=| Interquartile range
Due to its construction criteria, each section of the quartile diagram contains about 25% of the data in the distribution.
Using the following quartile diagram, determine if the statements are true or false and justify each of your answers.
1) About |50\ \%| of the data is included between |\color{green}{25}| and |\color{orange}{55}.|
2) The interquartile range is |65|.
3) There is more data between |\color{green}{25}| and |\color{red}{45}| than between |\color{red}{45}| and |\color{orange}{55}.|
4) The mean of the distribution is |\color{red}{45}.|
|
ANSWERS |
JUSTIFICATIONS |
|---|---|
|
1) True |
Each section contains approximately |25\ \%| of the data. Thus, 2 sections |\approx 50\ \%| of the data. |
|
2) False |
The interquartile range |= Q_3 - Q_1 = \color{orange}{55}-\color{green}{25} = 30|. |
|
3) False |
Each section contains about |25\ \%| of the data. Even though the rectangle is longer, it doesn't mean there's more data, it means it's more scattered. |
|
4) False |
The median is |\color{red}{45}.| It is not possible to calculate the average precisely with this kind of diagram. |
See also
To build a scatter plot, simply place each of the points found in the same context on a Cartesian plane by identifying them with a point.
To have a better idea of his players’ performance progress, a hockey coach analyzes the number of games played and the number of points obtained during the last three seasons.
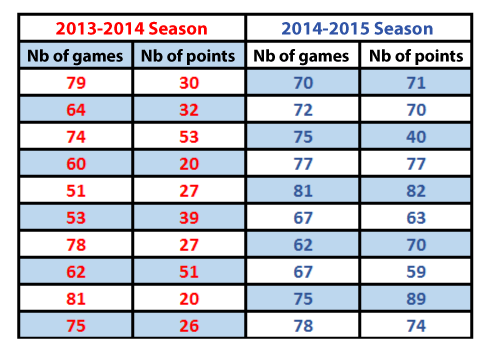
Construct a scatter plot with all the data to help sort it all out.
-
Identify the axes and the title.
-
Create a legend for each season.
|\color{red}{\bullet}:| 2013-2014 season
|\color{blue}{\bullet}:| 2014-2015 season -
Place each coordinate in the Cartesian plane.
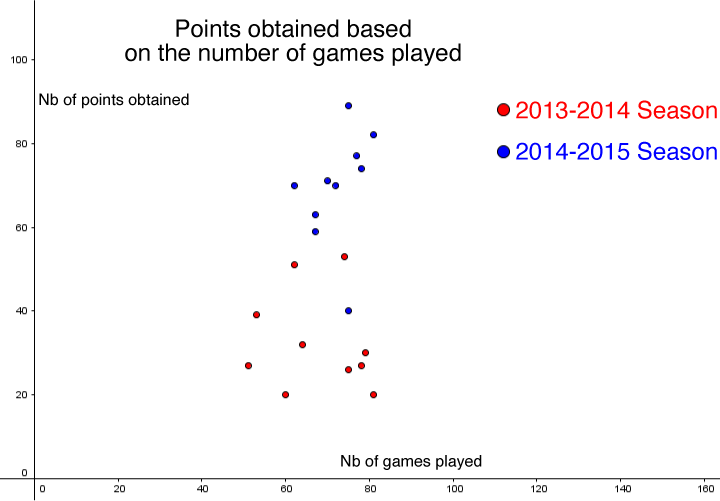
See also
|
Orthogonal projections (various views) |
|
|---|---|
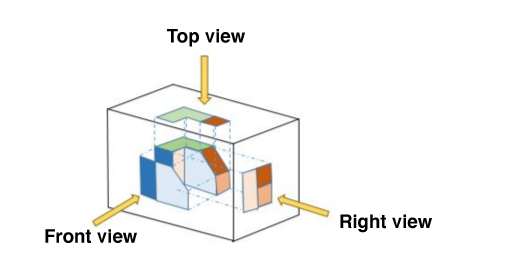 |
|
| Parallel projections | |
|
Isometric perspective (only the front face is not deformed) |
Axonometric perspective (edge measurements proportional to reality) |
| |
|
| Central projections | |
| Perspective with a vanishing point | Perspective with two vanishing points |
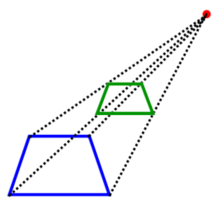 |
|
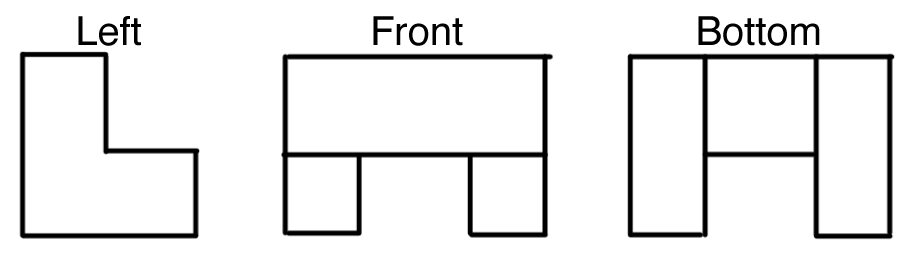
Based on the different views of an orthogonal projection presented above, which of the following solids can be associated with it?
|
DEDUCTIONS |
JUSTIFICATIONS |
|---|---|
|
1) Not A and B. |
The left view is not adequate. |
|
2) Not C. |
The front view is not adequate. |
|
The solid associated with the views presented is solid D. |
|
See also
-
|\text{Similarity ratio} = \dfrac{\text{Image figure dimensions}}{\text{Initial figure’s corresponding dimensions}}=k^1|
-
|\text{Ratio of Areas} = \dfrac{\text{Image figure area}}{\text{Initial figure area}}=k^2|
-
|\text{Ratio of Volumes} = \dfrac{\text{ volume of the image solid}}{\text{volume of the initial solid}}=k^3|
The arithmetic associations existing between each of the ratios are:
To keep every customer happy, a company sells party hats in two sizes: one for adults and one for kids. The height of the adult size is 7 cm higher than the child version.
Given that the ratio of the hat’s respective lateral areas is |\dfrac{49}{25},| what are the heights of both hats?
-
Calculate the value of |k^1.| ||\begin{align} k^1 &= \sqrt{k^2} \\ &= \sqrt{\dfrac{49}{25}} \\ &= \dfrac{7}{5} \end{align}||
-
Establish the proportion according to the ratio |k^1| already calculated. ||\dfrac{\color{red}{h+7}}{\color{blue}{h}} = \dfrac{7}{5}||
-
Solve the equation. ||\begin{align} 5 \color{red}{(h+7)} &= 7 \color{blue}{h} \\ 5h + 35 &= 7h \\ 35 &= 2h \\ 17{.}5 &= h \end{align}||
Answer: The children's hat has a height of |\color{blue}{h} = 17{.}5\ \text{cm}| and the adult model's height is |\color{red}{h+7} = 17{.}5 \color{red}{+7} = 24{.}5\ \text{cm}.|
See also
Since we are dealing with a decomposable solid, it’s better to work with the area of each of the solid’s faces rather than the total area of each of the solids that compose it. In other words, the area formulas of plane figures are preferred.
|
|A_\text{square} = s^2| |
|A_\text{rectangle} = b\times h| |
|A_\text{rhombus} = \displaystyle \frac{D \times d}{2}| |
|
|A_\text{parallelogram}=b \times h| |
|A_\text{trapezoid} = \displaystyle \frac{(B+b)\times h}{2}| |
|A_\text{triangle} = \displaystyle \frac{b \times h}{2}| |
|
|A_\text{circle}=\pi r^2| |
|A_\text{regular polygon}= \displaystyle \frac{s a n}{2}| |
|A_\text{cone}= \pi r^2 + \pi r a| |
|
|A_\text{cylinder}=2\pi r^2 + 2\pi r h| |
||
As a collector is browsing an antique store, she sees a chest. If she buys it, she will need to know its total height because it must be similar to the ones she already owns. For restoration purposes, the total area is known.
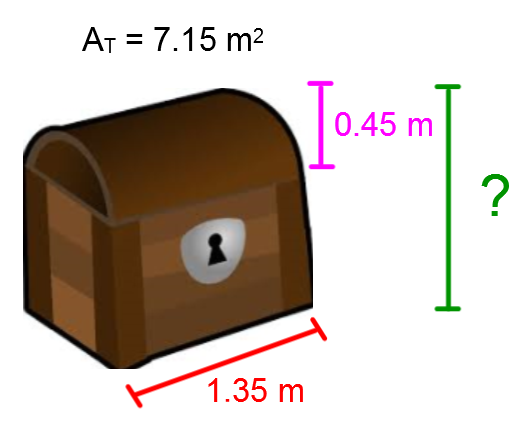
What is the total height of the chest?
-
Identify the missing measurement.
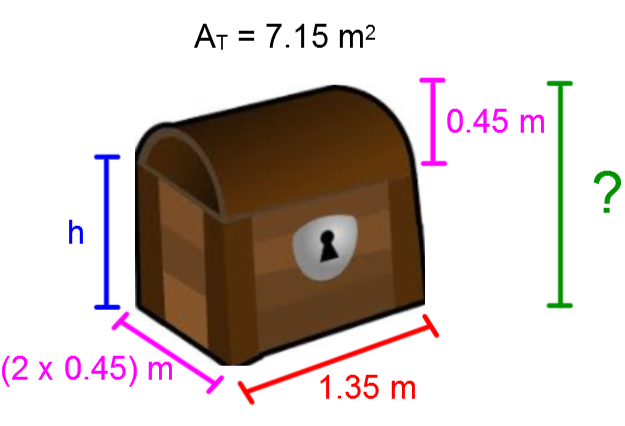
-
Create the equation for calculating the total area. ||\begin{align} A_\text{total} &= A_\text{base}+2 A_\text{left-right faces}+2 A_\text{front-back faces}+\dfrac{1}{2} A_\text{L cylinder}+A_\text{disc} \\ 7{.}15 &= \color{red}{1{.}35}\times \color{fuchsia}{0{.}9} + 2 (\color{fuchsia}{0{.}9}\times \color{blue}{h}) + 2 (\color{red}{1{.}35}\times \color{blue}{h}) + \frac{1}{2}(2 \pi \times \color{fuchsia}{0{.}45} \times \color{red}{1{.}35}) + \pi\times \color{fuchsia}{0{.}45}^2 \end{align}||
-
Solve the problem by finding the value of |\color{blue}{h}.| ||\begin{align} 7{.}15 &\approx 1{.}215 + 1{.}8\color{blue}{h} + 2{.}7\color{blue}{h} + 1{.}908+0{.}636 \\ 7{.}15 &\approx 3{.}759 + 4{.}5\color{blue}{h} \\ 3{.}391 &\approx 4{.}5\color{blue}{h} \\ 0{.}75 &\approx \color{blue}{h} \end{align}||
Answer: The total height of the chest | \approx \color{blue}{h} + \color{fuchsia}{0{.}45} \approx \color{blue}{0{.}75}+\color{fuchsia}{0{.}45} \approx 1{.}2 \ \text{m}.|
See also
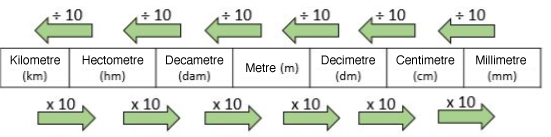
Length units
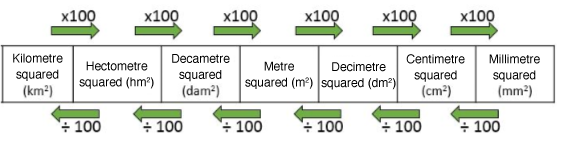
Area units
Volume units
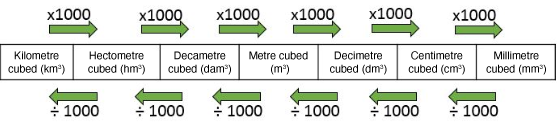
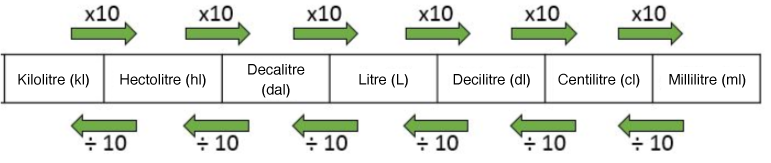
Capacity units
Volume and capacity
|
|1 \ \text{kL} = 1 \ \text{m}^3| |
|1 \ \text{L} = 1 \ \text{dm}^3| |
| 1 \ \text{mL} = 1 \ \text{cm}^3| |
A few years ago, a municipality offered to help people fill their pools. To avoid waste, the city provided free help from firefighters for the first |\color{blue}{5 \ 000}\ \text{L}| of water. For the rest, the city charged a fee of |$0{.}002\ | per additional litre.
How much would it cost to fill a swimming pool with a volume of |\color{red}{22 \ \text{m}^3}|?
-
Transform all data into the same unit. ||\begin{align} \color{red}{22 \ \text{m}^3} &= 22\ \text{kL} \\ &= 22 \ 000 \ \text{L} \end{align}||
-
Determine the amount of water that would cost money. ||\begin{align} \text{Water to pay} &= 22 \ 000 - \color{blue}{5 \ 000} \\ &= 17 \ 000\ \text{L} \end{align}||
Answer: The cost |= 17 \ 000 \times 0{.}002 = $34.|
See also
To calculate the volume of decomposable solids, it is important to remember the formulas for the volume of solids.
|
|V_\text{prism} = A_b \times h| |
|V_\text{cube} = s^3| |
|V_\text{pyramid} = \displaystyle \frac{A_b \times h}{3}| |
|
|V_\text{cylinder} = \pi r^2 \times h| |
|V_\text{sphere} = \displaystyle \frac{4 \pi r^3}{3}| |
|V_\text{cone} = \displaystyle \frac{\pi r^2 \times h}{3}| |
After making several purchases at your favorite furniture store, you use your own trailer to haul everything home. Due to regulations, your load must not exceed 3 m in height from the ground.
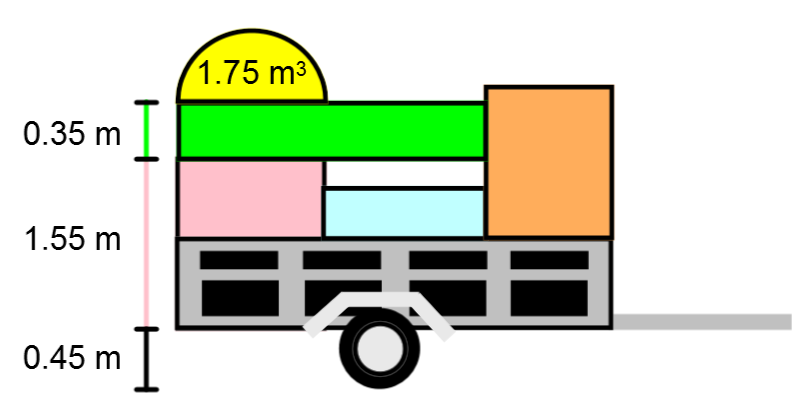
Based on the information you have, determine if your load is legal or not knowing that your trailer’s width is |\color{blue}{1{.}5}\ \text{m}.|
-
Identify the rule to use for the volume of a half cylinder. ||V = \dfrac{\pi r^2 \times\color{blue}{h}}{2}||
-
Replace the known values and isolate the remaining variable |r.| ||\begin{align} \color{orange}{1{.}75} &= \dfrac{\pi r^2 \times \color{blue}{1{.}5}}{2} \\ 3{.}5 &= 1{.}5 \pi r^2 \\ 0{.}74 &\approx r^2 \\ 0{.}86 &\approx r \end{align}||
Answer: Since the total height of the load |= 0{.}45 + \color{fuchsia}{1{.}55}+\color{green}{0{.}35} + \color{orange}{0{.}86} = 3{.}21\ \text{m},| your load is not legal, because |3{.}21 > 3.|
See also
|\color{blue}{a}^2 + \color{red}{b}^2 = \color{green}{c}^2|
Where
|\color{blue}{a}| and |\color{red}{b} = | measurement if the sides
|\color{green}{c} = | measurement of the hypotenuse
To save people from a fire, firefighters want to install a temporary bridge to allow people to pass from the burning building to safety.
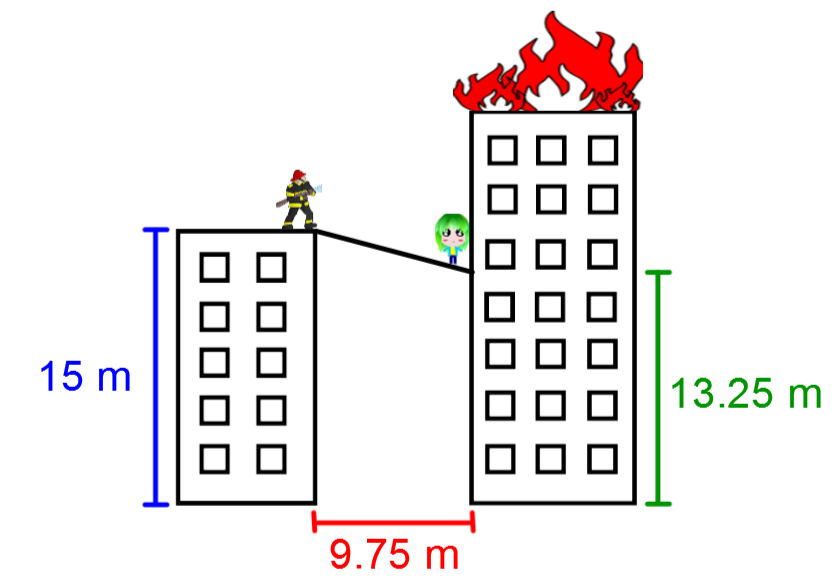
Based on the information in the drawing, what should be the minimum length of the bridge?
-
Identify the right triangle and its measurements. ||\begin{align} \color{blue}{\text{Side}_1} &=\color{blue}{a}= 15 - 13{.}25 = 1{.}75\ \text{m} \\ \color{red}{\text{Side}_2} &=\color{red}{b} = 9{.}75\ \text{m} \\ \color{green}{\text{Hypotenuse}} &= \color{green}{c} =\ ? \end{align}||

-
Apply the Pythagorean relationship. ||\begin{align} \color{blue}{a}^2 +\color{red}{b}^2 &= \color{green}{c}^2 \\ \color{blue}{1{.}75}^2 + \color{red}{9{.}75}^2 &= \color{green}{c}^2 \\98{.}125 &= \color{green}{c}^2 \\ 9{.}91 &\approx \color{green}{c} \end{align}||
Answer: The bridge must be a minimum of |9{.}91\ \text{m}.|
