Voici un petit guide de préparation contenant toutes les notions abordées en quatrième secondaire dans la séquence SN. Pour expliquer le tout, chaque formule sera suivie d'un exemple et d'un lien qui mène à une fiche de notre bibliothèque virtuelle.
La division de polynômes se fait de la même façon que la division de deux nombres en utilisant la méthode par « crochet ».
Quel est le résultat de la division suivante :
| CALCULS | EXPLICATIONS |
|---|---|
|
S'assurer qu'il y ait un terme pour chacun des |\color{blue}{degrés}| de |x.| |
|
|
Déterminer le |\color{red}{monôme}| par lequel il faut multiplier |2x^2 + x + 5| pour annuler le terme en |x^4| du polynôme. |
|
|
Déterminer le |\color{blue}{monôme}| par lequel il faut multiplier |2x^2 + x + 5| pour annuler le terme en |x^3| du polynôme. |
|
|
Déterminer le |\color{green}{monôme}| par lequel il faut multiplier |2x^2 + x + 5| pour annuler le terme en |x^2| du polynôme. |
|
|
Identifier le reste lorsque le degré du résultat de la soustraction est plus petit que celui du binôme par lequel on divise. |
|
|
Le résultat de la division est |2x^2 - 4x - 3| reste |5x - 32| ou |2x^2 - 4x - 3 + \dfrac{5x - 32}{2x^2 + x + 5}.| |
|
Pour additionner ou soustraire des expressions rationnelles, on peut généralement procéder en suivant les étapes ci-dessous :
-
Factoriser le numérateur et le dénominateur de chaque fraction.
-
Poser toutes les restrictions (dénominateurs différents de 0).
-
Simplifier les facteurs communs dans chacune des fractions, si possible.
-
Trouver un dénominateur commun.
-
Effectuer l'addition ou la soustraction au numérateur.
-
Simplifier l'expression rationnelle finale en factorisant le numérateur et le dénominateur, si possible.
Simplifie l'expression algébrique suivante :
|\displaystyle \frac{x-2}{x+5} - \frac{3}{-3x-12}|
| CALCULS | EXPLICATIONS |
|---|---|
|
|\begin{align} &\dfrac{x-2}{x+5} - \dfrac{3}{-3x-12} \\\\ =\ &\dfrac{x-2}{x+5}\color{red}{-}\dfrac{\color{red}{3}}{\color{red}{-3}(x+4)} \end{align}| |
Factoriser le numérateur et le dénominateur de chaque fraction. |
|
|\begin{align} x+5\neq 0\ &\rightarrow\ x\neq -5 \\ -3(x+4)\neq 0\ &\rightarrow\ x\neq -4 \end{align}| |
Poser les restrictions (dénominateurs différents de 0). |
|
|\begin{align} =\ &\dfrac{x-2}{x+5}\color{red}{-}\dfrac{\color{red}{3}}{\color{red}{-3}(x+4)} \\ =\ &\dfrac{x-2}{x+5}+\dfrac{1}{x+4} \end{align}| |
Simplifier les facteurs communs. Dans ce cas, on peut simplifier |\color{red}{-3}.| |
|
|=\ \dfrac{(x-2)\color{red}{(x+4)}}{(x+5)\color{red}{(x+4)}}+\dfrac{1 \color{red}{(x+5)}}{(x+4)\color{red}{(x+5)}}| |
Mettre les fractions sur un dénominateur commun. |
|
|\begin{align} =\ &\dfrac{(x-2)(x+4)+1(x+5)}{(x+4)(x+5)} \\ =\ &\dfrac{x^2-2x+4x-8+x+5}{(x+4)(x+5)} \\ =\ &\dfrac{x^2+3x-3}{(x+4)(x+5)} \end{align}| |
Effectuer l'opération sur les numérateurs et simplifier les termes semblables. |
|
|=\ \dfrac{x^2+3x-3}{(x+4)(x+5)}| |
Dans ce cas, il n'est pas possible de factoriser le numérateur à l'aide de la méthode produit-somme. Même en utilisant la complétion de carré, la factorisation ne permettrait pas de simplifier le numérateur et le dénominateur. |
|
Ainsi, le résultat de la différence de ces deux expressions rationnelles est |\dfrac{x^2+3x-3}{(x+4)(x+5)}| où |x\neq -4| et |x\neq -5.| |
|
Il est très important de maitriser le concept de distributivité associé à la multiplication :
-
Simplifier les expressions entre parenthèses, si possible.
-
Distribuer chacun des termes de la première parenthèse sur tous les termes de la deuxième parenthèse.
-
Simplifier en additionnant et soustrayant les termes semblables.
Quelle est l'expression algébrique simplifiée de la multiplication suivante : ||(7x+4)(2x^2-4x+3)||
| CALCULS | EXPLICATIONS |
|---|---|
|
|\begin{align} &(7x+4)(2x^2−4x+3)\\ |
Distribuer chacun des termes de la première parenthèse avec les termes de la deuxième parenthèse. |
|
|\begin{align} &14x^3 + −28x^2 + 21x + 8x^2 + −16x + 12 \\ =\ &14x^3 + −20x^2 + 5x + 12\end{align}| |
Effectuer les additions et les soustractions sur les termes semblables. |
|
L'expression algébrique simplifiée est : |14x^3 − 20x^2 + 5x + 12| |
|
À voir aussi
Pour factoriser une même expression algébrique, on doit parfois utiliser plusieurs méthodes de factorisation. Ainsi, il est important de maitriser chacune d'entre elles tout en y associant leur forme polynomiale caractéristique.
|
EXEMPLE DE LA MÉTHODE PRODUIT-SOMME |
|
|---|---|
|
Quelles mesures (sous forme numérique ou d'expression algébrique) peuvent être associées à chacune des dimensions d'un prisme à base rectangulaire dont le volume est de |4x^2+8x−32\ \text{cm}^3|? |
|
|
CALCULS |
EXPLICATIONS |
|
|\begin{align} &4x^2+8x−32 \\ =\ &4(x^2+2x−8)\end{align}| |
Si possible, faire une mise en évidence simple en s'assurant que tous les coefficients demeurent entier. |
|
|\begin{align} &4(\color{blue}{x^2}+\color{red}{2x}\color{green}{−8}) \\\\ P =\ &\color{blue}{1}\times \color{green}{−8}=−8 \\ S =\ &\color{red}{2} \end{align}| Les nombres sont |4| et |−2,| car |4\times -2 = -8| et |4+-2=2.| |
Déterminer les nombres qui répondent au produit et à la somme du polynôme entre parenthèse. |
|
|\begin{align} &4(x^2+\color{red}{2x}−8) \\ |
Séparer le terme en |\color{red}{x}| en utilisant les deux nombres trouvés et faire une mise en évidence double. |
|
Ainsi, les trois dimensions mesurent respectivement |4,| |(x+4)| et |(x−2)| cm. |
|
|
EXEMPLE DE DIFFÉRENCE DE CARRÉS |
|
|---|---|
|
Quelles sont les expressions algébriques qui représentent la mesure de la base et de la hauteur d'un triangle dont l'aire est de |(2x^2 −8)\ \text{m}^2\ ?| |
|
|
CALCULS |
EXPLICATIONS |
|
|\begin{align} \frac{\color{blue}{b}\times \color{red}{h}}{2} &= 2x^2 - 8 \\ \Rightarrow\ \color{blue}{b}\times \color{red}{h} &=4x^2 -16 \end{align}| |
Créer l'équation en lien avec la situation. |
|
|\begin{align} \sqrt{4x^2} &= 2x \\ \sqrt{16} &= 4 \end{align}| Il s'agit d'une soustraction entre les deux termes. |
Vérifier que le binôme répond aux critères d'une factorisation par différence de carrés. |
|
|\begin{align} \color{blue}{b} \times \color{red}{h} &= 4x^2 − 16 \\ \Rightarrow\ \color{blue}{b} \times \color{red}{h} &= \color{blue}{(2x−4)}\color{red}{(2x+4)} \end{align}| |
Factoriser selon le modèle suivant : |a^2-b^2=(a-b)(a+b)| |
|
Ainsi, on peut établir que |\color{blue}{b = (2x−4)}| et |\color{red}{h = (2x+4)}\ \text{m}.| |
|
|
EXEMPLE DE TRINÔME CARRÉ PARFAIT |
|
|---|---|
|
Quelle est l'expression algébrique associée à la mesure du côté d'un carré qui a une superficie de |\color{blue}{9}x^2 − \color{red}{42}x + \color{green}{49}\ \text{m}^2|? |
|
|
CALCULS |
EXPLICATIONS |
|
|\begin{align} \sqrt{\color{blue}{a}} &= \sqrt{\color{blue}{9}} = \color{blue}{3} \\ \sqrt{\color{green}{c}} &= \sqrt{\color{green}{49}} = \color{green}{7} \\\\ \color{red}{c} &\overset{?}{=} 2\sqrt{\color{blue}{a}}\sqrt{\color{green}{c}} \\ \Rightarrow\ \color{red}{42} &= 2\times \color{blue}{3} \times \color{green}{7} \end{align}| |
Vérifier qu'il s'agit bien d'un trinôme carré parfait. |
|
|\begin{align} &\color{blue}{9}x^2 − \color{red}{42}x + \color{green}{49} \\ =\ &(\color{blue}{3}x-\color{green}{7})^2 \end{align}| |
Factoriser selon le modèle du trinôme carré parfait. |
|
Puisque l'aire d'un carré se calcule avec la formule |A=c^2,| on peut déduire que |A=(\color{blue}{3}x-\color{green}{7})^2.| Par associativité, on obtient que |c=(\color{blue}{3}x-\color{green}{7})\ \text{m}.| |
|
| EXEMPLE SELON LA COMPLÉTION DE CARRÉ | |
|---|---|
|
Quelle est l'équation de cette parabole sous sa forme factorisée : ||f(x) = -3x^2 - \frac{1}{2}x + 6|| |
|
| CALCULS | EXPLICATIONS |
|
|\begin{align} &\color{blue}{-3}x^2 - \dfrac{1}{2}x + 6 \\ =\ &\color{blue}{-3}\left(x^2 + \color{red}{\dfrac{1}{6}}x - 2\right) \end{align}| |
Faire une mise en évidence simple pour s'assurer que le coefficient du terme en |x^2 = 1.| |
|
|\begin{align} &\left(\dfrac{\color{red}{b}}{2}\right)^2 \\ =\ &\left(\dfrac{\color{red}{\frac{1}{6}}}{2}\right)^2 \\ =\ &\color{green}{\frac{1}{144}} \end{align}| |
Calculer la valeur de |\left(\dfrac{\color{red}{b}}{2}\right)^2|. |
|
|\begin{align} &-3\left(x^2 + \frac{1}{6}x \color{green}{+ \frac{1}{144} - \frac{1}{144}} - 2\right) \\ = &-3 \left(\left[x^2 + \frac{1}{6}x \color{green}{+ \frac{1}{144}}\right] \color{green}{- \frac{1}{144}} - 2\right) \\ = &-3 \left(\left[x + \frac{1}{12}\right]^2 - \frac{289}{144}\right) \end{align}| |
Ajouter et soustraire cette valeur pour obtenir un trinôme carré parfait. |
|
|\begin{align} &-3 \left(\left[x + \frac{1}{12}\right]^2 - \frac{289}{144}\right) \\ = &-3 \left(\Big(x + \frac{1}{12} + \frac{17}{12}\Big)\Big(x + \frac{1}{12} - \frac{17}{12}\Big)\right) \\ = &-3 \left(x + \frac{18}{12}\right) \left(x - \frac{16}{12}\right) \\ = &-3 \left(x + \frac{3}{2}\right) \left(x - \frac{4}{3}\right) \end{align}| |
Effectuer une différence de carré avec les termes entre parenthèses. |
|
La forme factorisée de l'équation de départ est : |f(x) = -3 \left(x + \dfrac{3}{2}\right) \left(x - \dfrac{4}{3}\right).| |
|
| EXEMPLE SELON LA FORMULE QUADRATIQUE | |
|---|---|
|
Quelles sont les expressions algébriques ou les mesures que l'on peut associer aux mesures des trois dimensions d'un prisme à base rectangulaire dont le volume est |(\color{blue}{3}x^2 + \color{green}{4}x \color{red}{- 8})\ \text{mm}^3|? |
|
| CALCULS | EXPLICATIONS |
|
|\begin{align} &\dfrac{^-\color{green}{b} \pm \sqrt{\color{green}{b}^2 - 4 \color{blue}{a} \color{red}{c}}}{2 \color{blue}{a}} \\ =\ &\dfrac{^-\color{green}{4} \pm \sqrt{\color{green}{4}^2 - 4 (\color{blue}{3})(\color{red}{^-8})}}{2 (\color{blue}{3})} \end{align}| |
Appliquer la formule quadratique : |\dfrac{^-b \pm \sqrt{b^2 - 4ac}}{2a}| |
|
|\begin{align} &\dfrac{^-\color{green}{4} \pm \sqrt{\color{green}{4}^2 - 4 (\color{blue}{3})(\color{red}{^-8})}}{2 (\color{blue}{3})} \\ =\ &\dfrac{^-\color{green}{4} \pm \sqrt{112}}{2 (\color{blue}{3})} \end{align}| |
Simplifier le radicande. |
|
|\begin{align} &\dfrac{^-\color{green}{4} \pm \sqrt{112}}{2 (\color{blue}{3})} \\\\ \Rightarrow x_1=\ &\dfrac{^-\color{green}{4} + \sqrt{112}}{2 (\color{blue}{3})} &&\text{et}\ x_2 = \dfrac{^-\color{green}{4} - \sqrt{112}}{2 (\color{blue}{3})} \\ \Rightarrow x_1 \approx\ &1{,}1 &&\text{et}\ x_2\ \approx ^-2{,}43 \end{align}| |
Identifier les deux réponses possibles. |
|
|\color{blue}{3}x^2 + \color{green}{4}x \color{red}{- 8}= 3(x-1{,}1)(x-^-2{,}43)| |
Écrire la factorisation du polynôme initial. |
|
De façon arbitraire, on peut respectivement associer les mesures de largeur, de profondeur et de hauteur du prisme à |3\ \text{mm},| |(x-1{,}1)\ \text{mm}| et |(x+2{,}43)\ \text{mm}.| |
|
À voir aussi
Forme canonique : |f(x) = a(x-h)^2 + k| où |(h,k)| est la coordonnée du sommet.
Forme générale : |f(x) = ax^2 + bx + c|
Forme factorisée : |f(x) = a (x - z_1) (x - z_2)| où |z_1| et |z_2| sont les zéros de fonction de la parabole.
Avec les informations qui sont fournies dans le tableau ci-dessous, détermine l'équation de la parabole sous ses trois différentes formes.
| CALCULS | EXPLICATIONS |
|---|---|
|
|\begin{align} \color{blue}{f(x)} &= a (\color{blue}{x} - \color{red}{h})^2 + \color{red}{k} \\ \color{blue}{f(x)} &= a \left(\color{blue}{x} - \color{red}{\dfrac{-17}{20}}\right)^2 + \color{red}{\dfrac{-169}{32}} \\ \color{blue}{\dfrac{-61}{50}} &= a \left(\color{blue}{2} - \color{red}{\dfrac{-17}{20}}\right)^2 + \color{red}{\dfrac{-169}{32}} \\ \dfrac{1}{2} &= a \\\\ \Rightarrow\ f(x) &= \dfrac{1}{2} \left(x + \dfrac{17}{20}\right)^2 - \dfrac{169}{32} \end{align}| |
Pour trouver l'équation sous sa forme canonique, on remplace les coordonnées du sommet |\color{red}{(h,k) = (\frac{-17}{20}, \frac{-169}{32})}| pour ensuite trouver la valeur du paramètre |a| en substituant par la coordonnée d'un autre point |\color{blue}{(x,y) = (2, \frac{-61}{50})}|. |
|
|\begin{align} f(x) &= \dfrac{1}{2} \left(x + \dfrac{17}{20}\right)^2 - \dfrac{169}{32} \\ \Rightarrow\ f(x) &= \dfrac{x^2}{2} + \dfrac{17x}{20} - \dfrac{123}{25} \end{align}| |
Pour trouver l'équation sous sa forme générale, il suffit de développer l'exposant 2 de la forme canonique. |
|
|\begin{align} f(x) &= \frac{1}{2} \left(x + \frac{17}{20}\right)^2 - \frac{169}{32} \\ \Rightarrow\ f(x) &= \frac{1}{2} \left(x - \frac{12}{5}\right) \left(x + \frac{41}{10}\right) \end{align}| |
Pour trouver l'équation sous sa forme factorisée, on peut trouver les zéros de la fonction par la formule quadratique ou en factorisant par la complétion de carré. |
Pour la fonction polynomiale de degré 2 : |a \ne \dfrac{\Delta y}{\Delta x}|
À voir aussi
L'équation de la règle d'une fonction partie entière s'écrit sous la forme ||f(x) = a \left[ b(x-h)\right] + k||
où
|(h,k) = | Coordonnées d'un point plein
|{\mid}a{\mid} = | Distance verticale entre deux marches
|\dfrac{1}{\mid b \mid} = | Longueur d'une marche
Pour déterminer le signe de |a| et de |b,| on s'intéressera à l'ordre des points ouverts et fermés, la croissance et la décroissance du graphique :
Dans le cadre d'un nouveau programme de récompense, une épicerie offre des timbres qui permettent d'obtenir des réductions significatives sur l'achat d'articles ciblés.
Avec un montant d'achat minimum de 5 $, la caissière remet cinq timbres aux clients. Par la suite, pour chaque tranche de 22 $ additionnels, elle donne sept timbres de plus au client.
À l'aide de ces informations, dans quel intervalle devrait se situer le montant de la prochaine facture d'un client s'il veut obtenir 47 timbres?
| CALCULS | EXPLICATIONS |
|---|---|
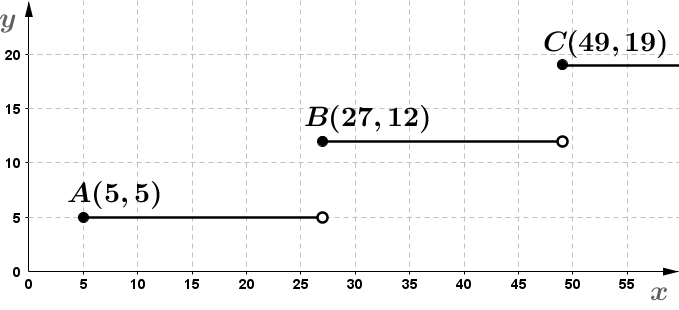 |
Tracer le graphique associé à cette situation. |
|
|\begin{align}{\mid}\color{red}{a}{\mid} &= 12 - 5 = 7 \\\\ \dfrac{1}{{\mid}\color{blue}{b}{\mid}} &= 27 - 5 = 22 \\ \Rightarrow\ {\mid}\color{blue}{b}{\mid} &=\dfrac{1}{22} \\\\ (h,k) &= (5,5) \end{align}| |
Trouver la valeur de |\mid \color{red}{ a} \mid,| de |\mid \color{blue}{b} \mid| et de |(h,k).| |
|
|\begin{align} f(x) &= \color{red}{a} \left[ \color{blue}{b}(x-h) \right] + k \\ \Rightarrow\ f(x) &= \color{red}{7} \left[ \color{blue}{\dfrac{1}{22}} ( x - 5) \right] + 5 \end{align}| |
Écrire l'équation de cette fonction en tentant compte de l'orientation des points ouverts et fermés. |
|
|\begin{align} f(x) &= \color{red}{7} \left[ \color{blue}{\dfrac{1}{22}}(x - 5)\right] + 5 \\ |
Trouver la valeur de |x| quand |f(x)| vaut |47.| |
|
|x \in \left[137, 159\right[| |
Déterminer l'intervalle en |x| de la solution. |
|
Ainsi, le montant d'achat doit être d'au moins |137\ $| mais de moins de |159\ $.| |
|
À voir aussi
La réciproque d'une fonction |f(x)|, notée |f^{-1}(x)|, s'obtient en inversant les coordonnées des points tel que |(x,y) \rightarrow (y,x)|
Trace la réciproque de la fonction suivante :
| CALCULS | EXPLICATIONS |
|---|---|
| |
Créer une table des valeurs selon les points donnés. |
| |
Inverser les coordonnées : |(\color{blue}{x}, \color{red}{y}) \rightarrow (\color{red}{y}, \color{blue}{x})| |
|
Tracer le graphique de la réciproque à l'aide de cette nouvelle table des valeurs. |
La réciproque d'une fonction ne donne pas toujours une fonction. Dans les cas étudiés ici, voici les fonctions qui sont réciproques les unes des autres :
-
les fonctions exponentielles et logarithmiques;
-
la fonction affine par rapport à elle-même;
-
la fonction de degré deux (avec un domaine restreint) et racine carrée.
À voir aussi
Pour l'étude d'une fonction, ce sont toujours les mêmes critères qu'il faut analyser :
-
le domaine : toutes les valeurs possibles de |x|
-
le codomaine (l'image) : toutes les avleurs possibles de |y|
-
les abscisses à l'origine (zéros) : la ou les valeur(s) du |x| quand |y=0|
-
l'ordonnée à l'origine : la valeur du |y| quand |x=0|
-
le maximum : la plus grande valeur de |y|
-
le minimum : la plus petite valeur de |y|
-
la croissance : quand le graphique ne « descend » pas
-
la décroissance : quand le graphique ne « monte » pas
-
le signe :
-
positive : portion du graphique qui est au-dessus ou égale à l'axe des |x|
-
négative : portion du graphique qui est en-dessous ou égale à l'axe des |x|
-
En tant que comptable d'une grande compagnie, tu dois donner un compte rendu détaillé de l'évolution des profits au cours de la dernière année. Pour t'aider, voici le graphique des 12 derniers mois.
Avant de préparer ton discours de présentation et afin d'alimenter ton argumentation, tu dois faire l'étude complète du graphique.
| Propriétés | EXPLICATIONS |
|---|---|
|
Domaine : |[0, 12]| |
La plus petite valeur sur l'axe des |x| est |0| et la plus grande est |12.| |
|
Image : |[-5, 20]| |
La plus petite valeur sur l'axe des |y| est |-5| et la plus grande est |20.| |
|
Croissance : |[0, 4] \cup [9, 12]| |
En analysant les valeurs de |x,| ce sont les deux portions du graphique qui montent ou qui sont constantes. |
|
Décroissance : |[4, 10]| |
En analysant les valeurs de |x,| c'est la seule portion du graphique qui descend ou qui est constante. |
|
Maximum : |\left\{ 20 \right\}| |
Selon les valeurs de |y,| c'est la plus grande valeur atteinte par le graphique. |
|
Minimum : |\left\{ -5 \right\}| |
Selon les valeurs de |y,| c'est la plus petite valeur atteinte par le graphique. |
|
Zéros de fonctions : |0,| |8| et |11| |
Ce sont les abscisses des points où le graphique touche à l'axe des |x.| |
|
Ordonnée à l'origine : |(0,0)| |
C'est la coordonnée du point où le graphique touche à l'axe des |y.| |
|
Positive : | [0,8] \cup [11,12]| |
Selon les valeurs de |x,| ce sont les portions du graphique qui sont au-dessus ou égales à l'axe des |x.| |
|
Négative : |\{0\}\cup [8,11]| |
Selon les valeurs de |x,| c'est la portion du graphique qui est en-dessous ou égale à l'axe des |x.| |
À voir aussi
Pour résoudre un système d'équations, on peut suivre les étapes suivantes :
-
Identifier les variables reliées aux inconnus.
-
Créer les équations selon la mise en situation.
-
Utiliser la méthode appropriée pour résoudre ce système (comparaison, substitution, réduction) selon l'allure des équations formées.
-
Remplacer la valeur de la variable dans une des équations de départ pour trouver la valeur de l'autre variable.
Afin de respecter les différentes contraintes imposées par la ville, un entrepreneur doit diviser son immense terrain boisé en deux différents lots rectangulaires.
En sachant que la superficie des terrains doit être la même, détermine les dimensions possibles, en décamètre, de ces deux terrains.
| CALCULS | EXPLICATIONS |
|---|---|
|
|x=| Mesure manquante (en dam) |y=| Aire des terrains (en dam2) |
Identifier les variables. |
|
|\begin{align} &\color{blue}{y = (2x-4) (x-7)} \\ &\color{red}{y = (x+8) (x-2)} \end{align}| |
Créer un système d'équations. |
|
|\begin{align} \color{blue}{(2x-4) (x-7)} &= \color{red}{(x+8)(x-2)} \\ \color{blue}{2x^2 - 18x + 28} &= \color{red}{x^2 + 6x - 16} \\ x^2 - 24x + 44 &= 0 \end{align}| |
Résoudre le système d'équations (par comparaison, substitution ou réduction). Dans ce cas présent, comme le |y| est isolé dans les deux équations, on utilisera la méthode de comparaison. |
| |\begin{align} x &= \dfrac{-b \pm \sqrt{b^2 - 4 a c}}{2a} \\ x &= \dfrac{-(-24) \pm \sqrt{(-24)^2 - 4 (1)(44)}}{2(1)} \\ x &= \dfrac{24 \pm 20}{2} \\ \Rightarrow\ x_1 &= \dfrac{24 + 20}{2} = 22\ \text{ et }\ x_2 = \dfrac{24 - 20}{2} = 2 \end{align}| |
Factoriser selon la méthode voulue (formule quadratique, double mise en évidence, complétion de carré, etc.). |
|
|\begin{align} &\color{blue}{(x-7)(2x - 4)} \\ \rightarrow\ &\color{blue}{(22-7)\big(2(22) - 4\big)}= \color{blue}{15 \times 40} \end{align}| |\begin{align} &\color{red}{(x+8) (x-2)} \\ \rightarrow\ &\color{red}{(22+8) (22-2) } = \color{red}{30 \times 20} \end{align}| |
Déterminer les mesures possibles selon |x_1 = 22.| |
|
|\begin{align} &\color{blue}{(x-7)(2x - 4)} \\ \rightarrow\ &\color{blue}{(2-7)\big(2 (2) - 4\big)} = \color{blue}{-5 \times 0} \end{align}| |\begin{align} &\color{red}{(x+8) (x-2)} \\ \rightarrow\ &\color{red}{(2+8) (2-2) } = \color{red}{10 \times 0} \end{align}| |
Déterminer les mesures possibles selon |x_2 = 2.| |
|
Puisque les mesures obtenues à l'aide de la valeur de |x_2| sont impossibles dans ce contexte (valeurs négatives ou nulles), on en déduit que les mesures du premier terrain sont de 15 dam par 40 dam et celles du deuxième sont de 20 dam par 30 dam. |
|
À voir aussi
Deux figures sont équivalentes lorsqu'elles ont la même aire.
Afin que le cout d'asphaltage de son nouveau stationnement résidentiel soit le même que celui de son ancien, Julien veut que ses deux entrées soient équivalentes.
Ainsi, quelle devrait être la mesure de la largeur de son nouveau stationnement?
| CALCULS | EXPLICATIONS |
|---|---|
|
|\color{red}{A_\text{ancien}} = \color{blue}{A_\text{nouveau}}| |
Les deux figures sont équivalentes. |
|
|\begin{align} \color{red}{A_\text{ancien}} &= \color{blue}{A_\text{nouveau}} \\ \color{red}{b\times h} &= \color{blue}{b\times h} \\ \color{red}{8 \times 12} &= \color{blue}{b \times 10} \\ \color{red}{96} &= \color{blue}{10b} \\ 9{,}6\ \text{m} &= \color{blue}{b} \end{align}| |
Créer une équation avec les formules d'aire et résoudre. |
|
La largeur de son nouveau stationnement doit être de |9{,}6\ \text{m}.| |
|
À voir aussi
Deux solides sont équivalents lorsqu'ils ont le même volume.
Une compagnie qui œuvre dans les accessoires de plein air veut offrir deux modèles de tente différents. Afin de conserver les mêmes couts de production, ils tiennent à ce que ces deux modèles soient équivalents.
Quelle devrait être la mesure de la hauteur du second modèle afin de respecter la condition de similitude?
| CALCULS | EXPLICATIONS |
|---|---|
|
|\color{blue}{V_\text{prisme}} = \color{red}{V_\text{demi-boule}}| |
Les deux solides sont équivalents. |
|
|\begin{align} \color{blue}{A_b \times h} &= \color{red}{\dfrac{4 \pi r^3}{3} \div 2} \\ \color{blue}{\dfrac{1{,}8 \times 1{,}7}{2} \times 2{,}1} &= \color{red}{\dfrac{4 \pi r^3}{6}} \\ \color{blue}{3{,}21} &\approx \color{red}{\frac{4 \pi r^3}{6}} \\ 1{,}53 &\approx \color{red}{r^3} \\ 1{,}15\ \text{m} &\approx \color{red}{r} \end{align}| |
Créer une équation avec les formules de volume respectives et résoudre. |
|
Le rayon de la tente en forme de demi-boule doit être d'environ |1{,}15\ \text{m}.| |
|
À voir aussi
En considérant l'angle |\theta| comme référence, on a :
|\sin \theta = \dfrac{\text{Mesure du côté opposé à }\ \theta}{\text{Mesure de l'hypoténuse}}|
|\cos \theta = \dfrac{\text{Mesure du côté adjacent à }\ \theta}{\text{Mesure de l'hypoténuse}}|
|\tan \theta = \dfrac{\text{Mesure du côté opposé à} \ \theta}{\text{Mesure du côté adjacent à} \ \theta}|
Afin de s'assurer de respecter les normes du bâtiment, l'angle d'élévation des fermes de toit d'une maison doit être d'un minimum de |25^\circ.| Pour s'assurer de respecter cette contrainte, un fabriquant décide d'établir cet angle à |35^\circ.| Si on sait que la longueur de la ferme de toit est de 13 mètres, quelles seront les mesures des deux autres côtés de cette pièce de bois?
| CALCULS | EXPLICATIONS |
|---|---|
|
|\sin \color{red}{35^\circ} = \dfrac{\color{red}{c}}{\color{green}{13}}| |
Identifier le bon rapport trigonométrique : |\sin \theta = \dfrac{\text{Opposé}}{\text{Hypoténuse}}| |
|
|\begin{align} \sin \color{red}{35^\circ} &= \dfrac{\color{red}{c}}{\color{green}{13}} \\ \color{green}{13}\sin \color{red}{35^\circ} &= \color{red}{c} \\ 7{,}46 &\approx \color{red}{c} \end{align}| |
Résoudre l'équation. |
|
|\cos \color{red}{35^\circ} = \dfrac{\color{blue}{b}}{\color{green}{13}}| |
Identifier le bon rapport trigonométrique : |\cos \theta = \dfrac{\text{Adjacent}}{\text{Hypoténuse}}| |
|
|\begin{align} \cos \color{red}{35^\circ} &= \dfrac{\color{blue}{b}}{\color{green}{13}} \\ \color{green}{13} \cos \color{red}{35^\circ} &= \color{blue}{b} \\ 10{,}65 &\approx \color{blue}{b} \end{align}| |
Résoudre l'équation. |
|
Ainsi, |\color{blue}{m \overline {AC}} \approx 10{,}65 \ \text{m}| et |\color{red}{m \overline {AB}} \approx 7{,}46 \ \text{m}.| |
|
Afin de déterminer le trajet à suivre par un hélicoptère pour aller chercher des gens en détresse en forêt, on a triangulé la carte de la région avec l'emplacement actuel de l'hélicoptère, l'hôpital et les gens qui sont en détresse.
Selon ce dessin, quelle orientation devrait suivre l'hélicoptère pour se rendre le plus rapidement possible aux gens en détresse?
| CALCULS | EXPLICATIONS |
|---|---|
|
|\tan ? = \dfrac{\color{red}{18{,}5}}{\color{blue}{12}}| |
Identifier le bon rapport trigonométrique : |\tan \theta = \dfrac{\text{Opposé}}{\text{Adjacent}}| |
|
|\begin{align} \tan ? &= \dfrac{\color{red}{18{,}5}}{\color{blue}{12}} \\ \tan ? &\approx 1{,}54 \\ ? &= \tan^{-1}(1{,}54) \\ ? &\approx 57^\circ \end{align}| |
Résoudre l'équation. |
|
L'angle d'orientation de l'hélicoptère devrait être de |57^\circ.| |
|
À voir aussi
Selon le triangle quelconque qui suit, on peut en déduire une série d'équivalences.
|\dfrac{a}{\sin A} = \dfrac{b}{\sin B} = \dfrac{c}{\sin C}|
Lors de certaines festivités westerns, des courses de chevaux sont organisées pour animer le spectacle. Lors de ces courses, les cowboys doivent faire le tour de chacun des trois barils qui sont disposés en forme de triangle isocèle.
À l'aide des mesures données, quelle est la distance entre chacun des barils?
| CALCULS | EXPLICATIONS |
|---|---|
| |
Identifier les sommets et les arêtes du triangles. |
| |
Si possible, déduire d'autres mesures du triangle (somme des angles intérieurs d'un triangle et propriétés du triangle isocèle). |
|
|\begin{align} \dfrac{\color{green}{a}}{\sin 40^\circ} &= \displaystyle \dfrac{\color{blue}{20}}{\sin \color{blue}{70^\circ}} \\\\ \Rightarrow\ \color{green}{a} &= \dfrac {\color{blue}{20} \sin 40^\circ}{\sin \color{blue}{70^\circ}} \\ \color{green}{a} &\approx 13{,}68 \ \text{m} \end{align}| |
Appliquer la loi des sinus et isoler la variable. |
|
Ainsi, |m \overline{AB} = m \overline {AC} = 20 \ \text{m}| et |m \overline {BC} \approx 13{,}68 \ \text{m}| |
|
Afin d'assurer un aérodynamisme maximal, le profil de certains voitures de course ressemble à un triangle.
Afin que ces proportions soient conservées, quelle devrait être la mesure de l'angle qui se situe près de la roue arrière?
| CALCULS | EXPLICATIONS |
|---|---|
| |
Identifier les sommets et les arêtes du triangle. |
|
|\begin{align} \dfrac{\color{blue}{1{,}18}}{\sin \color{blue}{15}} &= \dfrac {\color{red}{3{,}39}}{\sin \color{red}{B}} \\\\ \Rightarrow\ \sin \color{red}{B} &= \dfrac{\color{red}{3{,}39} \sin \color{blue}{15}}{\color{blue}{1{,}18}} \\ \sin \color{red}{B} &\approx 0{,}744 \end{align}| |
Utiliser la loi des sinus et isoler le sinus de l'angle recherché. |
|
|\begin{align} \sin \color{red}{B} &\approx 0{,}744 \\ \color{red}{ B} &\approx \sin^{-1} (0{,}744) \\ \color{red}{B} &\approx 48{,}1^\circ \end{align}| |
Calculer la valeur de la variable en effectuant |\sin^{-1}.| |
|
|\begin{align} \color{red}{m\angle B} &\approx 180^\circ - 48{,}1^\circ \\ \color{red}{m\angle B} &\approx 131{,}9^\circ \end{align}| |
Trouver la valeur de l'angle obtus. |
|
Dans cette situation, la mesure de l'angle est de |131{,}9^\circ.| |
|
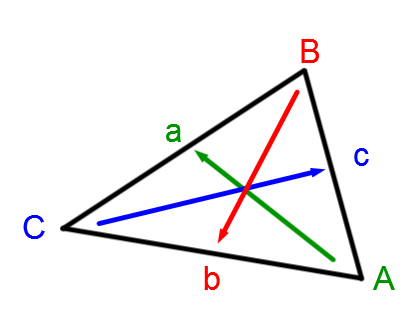
Quand on identifie le triangle, il est toujours essentiel de mettre
-
|\color{green}{\text{le côté a opposé à l'angle A}}|
-
|\color{red}{\text{le côté b opposé à l'angle B}}|
-
|\color{blue}{\text{le côté c opposé à l'angle C}}|
À voir aussi
Selon le triangle quelconque qui suit, on peut en déduire trois équivalences.
|a^2 = \color{blue}{b}^2 + \color{red}{c}^2 - 2 \color{blue}{b} \color{red}{c} \cos A|
|\color{blue}{b}^2 = a^2 + \color{red}{c}^2 - 2 a \color{red}{c} \cos \color{blue}{B}|
|\color{red}{c}^2 = a^2 + \color{blue}{b}^2 - 2 a \color{blue}{b} \cos \color{red}{C}|
Afin de maximiser ses chances de chasser un orignal, un chasseur à l'arc s'installe dans un coin de son terrain et la portée de ses flèches se décrit selon le triangle suivant :
En te fiant aux informations sur ce dessin, sur quelle |\color{red}{\text{distance}}| est-ce que l'orignal peut se promener en restant le plus loin possible du chasseur?
| CALCULS | EXPLICATIONS |
|---|---|
| |
Identifier les sommets et les arêtes du triangle. |
|
|\begin{align} \color{red}{a}^2 &= \color{blue}{b}^2 + \color{green}{c}^2 - 2\color{blue}{b} \color{green}{c} \cos \color{red}{A} \\ \color{red}{a}^2 &= \color{blue}{92}^2 + \color{green}{125}^2 - 2 \color{blue}{(92)} \color{green}{(125)} \cos \color{red}{81^\circ} \end{align}| |
Appliquer la formule appropriée pour faire en sorte qu'il n'y ait qu'une seule inconnue. |
|
|\begin{align} \color{red}{a}^2 &= \color{blue}{92}^2 + \color{green}{125}^2 - 2 \color{blue}{(92)} \color{green}{(125)} \cos \color{red}{81^\circ} \\ \color{red}{a}^2 &\approx 8\ 464 + 15\ 625 - 3\ 598 \\ \color{red}{a}^2 &\approx 20\ 491 \\ \color{red}{a}\ &\approx 143{,}15 \end{align}| |
Résoudre l'équation en isolant la variable. |
|
L'orignal peut se promener sur une |\color{red}{\text{distance}}| d'environ |143{,}15\ \text{m}.| |
|
Afin d'assurer la sécurité de ses employés, une banque fait installer une caméra de surveillance rotative dans le hall d'entrée. Par ailleurs, un agent de sécurité est également en charge de surveiller cette même région qui est définie par le triangle suivant:
Afin de s'assurer qu'il n'y ait aucun angle mort, quelle devrait être la mesure de l'angle de rotation de la caméra?
| CALCULS | EXPLICATIONS |
|---|---|
| |
Identifier les sommets et les arêtes du triangle. |
|
|\begin{align} \color{blue}{a^2} &= \color{red}{b^2} + \color{green}{c^2} - 2 \color{red}{b} \color{green}{c} \cos \color{blue}{A} \\ \color{blue}{22^2} &= \color{red}{24^2} + \color{green}{21^2} - 2 \color{red}{(24)} \color{green}{(21)} \cos \color{blue}{A} \end{align}| |
Substituer les valeurs dans la formule. Ici, on utilise |a^2 = b^2 + c^2 - 2bc \cos A| puisque c'est la mesure de l'angle |A| que l'on cherche. |
|
|\begin{align} \color{blue}{22^2} &= \color{red}{24^2} + \color{green}{21^2} - 2 \color{red}{(24)} \color{green}{(21)} \cos \color{blue}{A} \\ \color{blue}{484} &=576+441 - 1 \ 008 \cos \color{blue}{A}\\\\ \Rightarrow\ \dfrac{484 - 576-441}{- 1 \ 008} &= \cos \color{blue}{A} \\ 0{,}529 &\approx \cos \color{blue}{A} \\ 58^\circ &\approx \color{blue}{m\angle A} \end{align}| |
Isoler la variable. |
|
Pour s'assurer qu'il n'y ait aucun angle mort, la caméra devrait décrire des rotations d'un angle d'environ |58^\circ.| |
|
À voir aussi
Pour y arriver, il faut ajouter des lignes (généralement une hauteur) avec des propriétés particulières et des mesures indéterminées.
-
Choisir le bon sommet à partir duquel on trace une hauteur.
-
Utiliser les rapports trigonométriques dans le triangle rectangle pour trouver les mesures manquantes.
-
Appliquer la formule d'aire d'un triangle avec les mesures trouvées.
Quelle est l'aire du triangle suivant :
| CALCULS | EXPLICATIONS |
|---|---|
| |
Trouver toutes les mesures d'angle, si possible (Somme des angles intérieurs d'un triangle |= 180^\circ|). |
| |
Tracer une hauteur pour faire en sorte qu'elle soit l'inconnue dans le rapport trigonométrique utilisée. |
| |
Identifier le triangle rectangle ainsi formé. |
|
|\begin{align} \sin \color{red}{24^\circ} &= \dfrac{\color{blue}{h}}{42} \\ 17{,}08 &\approx \color{blue}{h} \\\\ \cos \color{red}{24^\circ} &= \dfrac{\color{green}{b}}{42} \\ 38{,}37 &\approx \color{green}{b} \end{align}| |
Trouver le plus de mesures possible à l'aide des rapports trigonométriques. |
| |
Trouver les mesures d'angle manquantes du petit triangle de gauche. |
|
|\begin{align} \tan \color{red}{48^\circ} &= \dfrac{\color{blue}{17{,}08}}{\color{green}{2^\text{e}\text{ cathète}}} \\ 15{,}38 &\approx \color{green}{2^\text{e}\text{ cathète}} \end{align}| |
Trouver la mesure de la 2e cathète du petit rectangle. |
| |
Déduire la mesure de la base du triangle initiale. |
| |
Identifier la base et la hauteur à utiliser pour calculer l'aire du triangle. |
|
|\begin{align} A &= \dfrac{b \times \color{blue}{h}}{2} \\ A &= \dfrac{22{,}99 \times \color{blue}{17{,}08}}{2} \\ &\approx 196{,}33 \ \text{cm}^2 \end{align}| |
Calculer l'aire du triangle selon sa formule. |
|
L'aire du triangle est d'environ |196{,}33 \ \text{cm}^2.| |
|
À voir aussi
-
A - C - A : Deux triangles sont isométriques quand une paire de côtés homologues isométriques est incluse entre deux paires d'angles homologues isométriques.
-
C - A - C : Deux triangles sont isométriques quand une paire d'angles homologues isométriques est incluse entre deux paires de côtés homologues isométriques.
-
C - C - C : Deux triangles sont isométriques quand chacune des paires de côtés homologues sont isométriques.
Dû à des problèmes de machinerie, les employés d'une compagnie de construction doivent monter eux-mêmes les fermes de toit de forme triangulaire afin de terminer la construction d'une maison. Or, ils doivent s'assurer qu'elles soient toutes identiques.
Avec les informations fournies ci-dessus, démontre que ces deux constructions sont isométriques.
| AFFIRMATIONS | JUSTIFICATIONS |
|---|---|
|
|\angle \color{red}{BAC} \cong \angle \color{green}{EFG}| |
|m \angle \color{green}{EFG} = 180^\circ - 130^\circ - 17^\circ = 33^\circ = m \angle \color{red}{BAC}| |
|
|\color{red}{\overline{AB}} \cong \color{green}{\overline{EF}}| |
Par hypothèse |
|
|\angle \color{red}{ABC} \cong \angle \color{green}{DEF}| |
Par hypothèse |
|
Le |\Delta \color{red}{ABC} \cong \Delta \color{green}{DEF}| par la condition minimale de A-C-A. |
|
À voir aussi
-
A - A : Deux triangles sont semblables quand deux paires d'angles homologues sont isométriques.
-
C - A - C : Deux triangles sont semblables quand une paire d'angles homologues isométriques est incluse entre deux paires de côtés homologues proportionnels.
-
C - C - C : Deux triangles sont semblables si les trois paires de côtés homologues sont proportionnels.
Dans le cadre d'une levée de fonds pour un organisme communautaire, la ville organise une course à pied à faire en famille. Par ailleurs, ils tiennent à ce que le trajet fait par les adultes soit semblable à celui des enfants.
En tenant compte des informations données ci-dessus, démontre que les deux trajets sont semblables.
| AFFIRMATIONS | JUSTIFICATIONS |
|---|---|
|
|\dfrac{m\color{green}{\overline{AC}}}{m \color{blue}{\overline {DF}}} = \dfrac{m\color{green}{\overline{AB}}}{m \color{blue}{\overline {DE}}}= \dfrac{m\color{green}{\overline{BC}}}{m \color{blue}{\overline {EF}}}| |
|\begin{align} \dfrac{\color{green}{1{,}4}}{\color{blue}{3{,}5}} &= \dfrac{\color{green}{1{,}1}}{\color{blue}{2{,}75}}= \dfrac{\color{green}{0{,}8}}{\color{blue}{2}} \\ \dfrac{2}{5}\ \ &=\ \ \dfrac{2}{5}\ \ \ =\ \ \dfrac{2}{5}\end{align}| |
|
Ainsi, |\Delta \color{green}{ABC} \sim \Delta \color{blue}{DEF}| par la condition minimale C-C-C. |
|
À voir aussi
Selon le triangle rectangle qui suit, on peut en déduire 3 théorèmes.
-
Dans un triangle rectangle, la mesure de chaque côté de l’angle droit est moyenne proportionnelle entre la mesure de sa projection sur l’hypoténuse et celle de l’hypoténuse entière.||\begin{align} \dfrac{m}{a} = \dfrac{a}{c}\ &\Leftrightarrow\ a^2 = m c \\\\ \dfrac{n}{b} = \dfrac{b}{c}\ &\Leftrightarrow\ b^2 = n c \end{align}||
-
Dans un triangle rectangle, la mesure de la hauteur issue du sommet de l’angle droit est moyenne proportionnelle entre les mesures des deux segments qu’elle détermine sur l’hypoténuse. ||\dfrac{m}{h} = \dfrac{h}{n}\ \Leftrightarrow\ h^2 = m n||
-
Dans le triangle rectangle, le produit des mesures de l’hypoténuse et de la hauteur correspondante égale le produit des mesures des côtés de l’angle droit. ||c h = a b||
Afin de se distinguer des autres entrepreneurs, une compagnie de construction suggère des maisons avec des toits de différentes formes. Parmi ces choix, on a la forme suivante :
Afin d'estimer les couts de production, l'entrepreneur a besoin des deux mesures extérieures manquantes de ce triangle |(\overline {AB}, \overline {BC}).| Aide-le à les déterminer.
| CALCULS | EXPLICATIONS |
|---|---|
|
|\begin{align} &a\; = 6{,}5 \\ &m = 4{,}1 \\ &c \ (m\overline {AB}) =\ ? \\ &b \ (m\overline {BC}) =\ ? \end{align}| |
Associer toutes les mesures connues et recherchées à une des mesures du dessin de référence. |
|
|\begin{align} a^2 &= m c \\ 6{,}5^2 &= 4{,}1 c \end{align}| |
Choisir le théorème pour laquelle on aura une seule inconnue : Dans un triangle rectangle, la mesure de chaque côté de l’angle droit est moyenne proportionnelle entre la mesure de sa projection sur l’hypoténuse et celle de l’hypoténuse entière. |
|
|\begin{align} 6{,}5^2 &= 4{,}1 c \\ 42{,}25 &= 4{,}1 c \\ \dfrac{42{,}25}{\color{red}{4{,}1}} &= \dfrac{4{,}1c}{\color{red}{4{,}1}} \\ 10{,}3 &\approx c \end{align}| |
Résoudre l'équation. |
|
|\begin{align} a^2 + b^2 &= c^2 \\ 6{,}5^2 + m\overline {BC}^2 &= 10{,}3^2 \\ 42{,}25 + m\overline {BC}^2 &\approx 106{,}09 \\ m\overline {BC}^2 &\approx 63{,}84 \\ m\overline {BC} &\approx 8 \end{align}| |
Appliquer la relation de Pythagore dans le grand triangle rectangle vert pour trouver la mesure de la cathète manquante. |
|
Ainsi, |m \overline {AB} \approx 10{,}3 \ \text{m}| et |m \overline {BC} \approx 8 \ \text{m}.| |
|
À voir aussi
|\text{Distance} = \sqrt{(y_2 - y_1)^2 + (x_2 - x_1)^2}|
où
|(x_1, y_1):| Coordonnées du point situé au début du segment
|(x_2, y_2):| Coordonnées du point situé à l'autre extrémité du segment
Afin de déterminer la quantité d'essence qu'un avion doit avoir dans son réservoir pour faire un vol Montréal-Paris, on représente chacune de ces deux villes sur un plan cartésien gradué en kilomètre.
Quelle est la distance, en kilomètres, entre ces deux villes?
| CALCULS | EXPLICATIONS |
|---|---|
|
Montréal |= (\color{blue}{x_1}, \color{red}{y_1}) = (\color{blue}{512}, \color{red}{647})| |
Identifier les points |(x_1, y_1)| et |(x_2, y_2).| |
|
|\begin{align} \text{Distance} &= \sqrt{(y_2 - \color{red}{y_1})^2 + (\color{green}{x_2} - \color{blue}{x_1})^2} \\ \text{Distance} &= \sqrt{(1\ 603 - \color{red}{647})^2 + (\color{green}{5\ 936} - \color{blue}{512})^2} \end{align}| |
Substituer les valeurs dans la formule. |
|
|\begin{align} \text{Distance} &= \sqrt{(1\ 603 - \color{red}{647})^2 + (\color{green}{5\ 936} - \color{blue}{512})^2} \\ \text{Distance} &= \sqrt{ 956^2 + 5\ 424^2} \\ \text{Distance} &\approx 5\ 507{,}6 \ \text{km} \end{align}| |
Résoudre l'équation. |
|
La distance entre Montréal et Paris est d'environ |5\ 507{,}6 \ \text{km}.| |
|
À voir aussi
Les droites |y_1 = a_1 x + b_1| et |y_2 = a_2 x + b_2| sont parallèles si et seulement si |a_1 = a_2.|
Quelle est l'équation de la droite qui est parallèle à celle identifiée dans le plan cartésien ci-dessous et qui passe par le point C?
| CALCULS | EXPLICATIONS |
|---|---|
|
|a = \dfrac{\Delta y}{\Delta x} = \dfrac{0{,}7 - 2{,}5}{1{,}5 - 0} = -1{,}2| |
Trouver la pente de |\overline{AB}.| |
|
|\begin{align} y &= -1{,}2x + b \\ 2{,}25 &= -1{,}2 (1{,}55) + b \\ 2{,}25 &= -1{,}86 + b \\ 4{,}11 &= b \end{align}| |
Trouver l'équation de la droite passant par |C (1{,}55 ; 2{,}25)| sous la forme |y = ax + b.| Dans ce cas, la valeur de |a| de l'équation recherchée est la même que celle de |\overline{AB}| puisque les droites sont parallèles. |
|
Finalement, l'équation de la droite qui est parallèle à |\overline{AB}| et qui passe par le point | C (1{,}55 ; 2{,}25)| est |y = -1{,}2x + 4{,}11.| |
|
Les droites |y_1 = a_1 x + b_1| et |y_2 = a_2 x + b_2| sont perpendiculaires si et seulement si |a_1 \times a_2 = -1.|
On dit aussi que deux droites sont perpendiculaires si la pente de l'une est l'opposée de l'inverse de la pente de l'autre : |a_2 = \dfrac{-1}{a_1}.|
Quelle est l'équation de la droite qui est perpendiculaire à celle identifiée dans le plan cartésien ci-dessous et qui passe par le point C?
| CALCULS | EXPLICATIONS |
|---|---|
|
|a_1 = \dfrac{\Delta y}{\Delta x} = \dfrac{0{,}7 - 2{,}5}{1{,}5 - 0} = -1{,}2| |
Trouver la pente de |\overline{AB}.| |
|
|\begin{align} a_1 \times a_2 &= -1 \\-1{,}2 \times a_2 &= -1 \\ a_2 &= \dfrac{-1}{-1{,}2} \\ a_2 &= 0{,}8\overline{3} \end{align}| |
Trouver la valeur de |a_2| de la droite passant par C en utilisant le fait que le produit des pentes de deux droites perpendiculaires vaut |-1.| |
|
|\begin{align} y &= a_2 x + b \\ y &= 0{,}8\overline{3}x + b \\ 2{,}25 &= 0{,}8\overline{3} (1{,}55) + b \\ 2{,}25 &\approx 1{,}29 + b \\ 0{,}96 &\approx b \end{align}| |
Trouver la règle de la droite passant par |C (1{,}55 ; 2{,}25)| sous la forme |y = a_2x + b.| |
|
Finalement, l'équation de la droite qui est perpendiculaire à |\overline{AB}| et qui passe par le point |C(1{,}55 ; 2{,}25)| est |y=0{,}8\overline{3}x + 0{,}96.| |
|
À voir aussi
Le nuage de points est utilisé pour estimer la corrélation qui existe entre deux variables. Pour avoir une idée plus précise de la corrélation, il faut calculer le coefficient de corrélation .
Depuis cinq ans, une nouvelle entreprise ne cesse d'augmenter ses profits et cherche à agrandir son centre de production. Par contre, elle veut s'assurer que la croissance économique de sa compagnie soit positive et fortement régulière. Pour analyser le tout, voici le recensement des revenus commerciaux des 30 dernières semaines.
À ton avis, est-ce que la croissance économique de l'entreprise est positive et fortement régulière?
| CALCULS | EXPLICATIONS |
|---|---|
| |
Tracer le nuage de points. |
| |
Comparer le nuage de points à ceux qui servent de référence. |
|
Selon le nuage de points tracé, on peut conclure que les revenus sont positifs et moyennement réguliers. Puisqu'ils ne sont pas fortement réguliers, il serait préférable d'attendre avant d'agrandir. |
|
À voir aussi
Après avoir encadré le nuage de points et pris la mesure de la longueur |(L)| et la largeur |(l)| du rectangle :
|r \approx \pm \left(1 - \dfrac{l}{L}\right)|
Pour ce qui est du signe, il sera donné en fonction du sens du nuage de points.
On peut également utiliser ce coefficient pour qualifier la corrélation :
| Valeur de |r| | Force du lien linéaire |
|---|---|
| Près de |0| | Nulle |
| Près de |\pm 0{,}50| | Faible |
| Près de |\pm 0{,}75| | Moyenne |
| Près de |\pm 0{,}87| | Forte |
| Près de |\pm 1| | Très forte |
| |\pm 1| | Parfaite |
Afin de faire un bilan sur la réussite des étudiants qui s'inscrivent dans les établissements d'enseignements pour adultes, les membres de la direction s'intéressent à la corrélation entre l'absentéisme aux différents cours (en heures) et la moyenne générale (en %) à la fin de l'année scolaire. Pour bien analyser le tout, ils ont regroupé les données dans un nuage de points :
Quel est le coefficient de corrélation de cette étude?
| CALCULS | EXPLICATIONS |
|---|---|
| |
Tracer un rectangle, le plus petit possible, afin d'encadrer le nuage de points. |
| |
À l'aide d'une règle, mesurer la longueur |(L)| et la largeur |(l)| du rectangle. Dans ce cas, |\color{blue}{L = 13{,}5 \ \text{cm}}| |\color{red}{l = 2{,}8 \ \text{cm}}| |
|
|\begin{align} r &\approx \pm \left(1 - \dfrac{\color{red}{2{,}8}}{\color{blue}{13{,}5}}\right) \\ r &\approx \pm 0{,}79 \end{align}| |
Remplacer |L| et |l| dans la formule |r \approx \pm \left(1 - \frac{\color{red}{l}}{\color{blue}{L}}\right).| |
|
|r \approx - 0{,}79| |
Puisque le rectangle est orienté vers le bas (décroissant), le coefficient de corrélation est négatif. |
|
Le coefficient de corrélation entre le nombre d'heures d'absence et le résultat final en pourcentage est d'environ |-0{,}79,| ce qui signifie une corrélation négative moyenne. |
|
À voir aussi
Pour trouver l'équation de la droite de régression selon la méthode médiane-médiane, on peut se fier aux étapes suivantes :
-
Mettre les couples en ordre croissant selon la valeur des |x.|
-
Séparer les couples en trois groupes égaux, si possible.
-
Calculer la coordonnée médiane |(M_1, M_2, M_3)| de chacun des groupes.
-
Calculer la coordonnée moyenne |(P_1)| des trois points médians.
-
Calculer la valeur de la pente |(a)| avec |M_1| et |M_3.|
-
Calculer la valeur de la valeur initiale |(b)| avec |P_1.|
-
Écrire l'équation de la droite de régression sous la forme |y = ax + b.|
Avant de construire une nouvelle tour à condo et d'en faire l'emménagement paysager, on s'intéresse à la hauteur des arbres afin qu'ils ne cachent pas la vue aux futurs résidents pour au moins les 20 prochaines années. Pour estimer la hauteur de ces derniers, on utilise la table de valeurs suivante :
À l'aide de ces informations, détermine à quelle hauteur devrait se situer les premiers balcons afin que la vue ne soit pas obstruée par les arbres.
| CALCULS | EXPLICATIONS |
|---|---|
| |
Placer les couples en ordre croissant selon la valeur de la variable indépendante |(x)| en prenant soin de ne pas « défaire » les couples initiaux. |
| |
Séparer les couples en trois groupes égaux. Si ce n'est pas possible, on s'assure que le premier et le dernier groupe aient le même nombre de données. |
|
|M_1 = (1 , 29)| |M_2 = (\dfrac{2+3}{2}, \dfrac{54+58}{2}) = (2{,}5 ; 56)| |M_3 = (4 , 90)| |
Calculer la coordonnée médiane de chaque groupe. |
|
|\begin{align} \color{green}{P} &= \left(\frac{1 + 2{,}5 + 4}{3} , \frac{29 + 56 + 90}{3}\right) \\ &= \color{green}{(2{,}5 ; 58{,}33)} \end{align}| |
Calculer le point moyen en faisant la moyenne des |x| et des |y| des trois points médians. |
|
|\color{blue}{a} = \dfrac{\Delta y}{\Delta x} = \dfrac{90 - 29}{4 - 1} \approx 20{,}33| |
Selon l'équation de la droite de régression |y = \color{blue}{a}x + \color{red}{b}|, déterminer la valeur de |\color{blue}{a}| selon les points |M_1| et |M_3.| |
|
|\begin{align} y &= \color{blue}{20{,}33} x + \color{red}{b}\\ \color{green}{58{,}33} &= \color{blue}{20{,}33}(\color{green}{2{,}5}) + \color{red}{b} \\ \color{red}{7{,}503} &= \color{red}{b} \end{align}| Ainsi, |y = \color{blue}{20{,}33} x + \color{red}{7{,}503}| |
Trouver la valeur du paramètre |\color{red}{b}| en substituant |x| et |y| par les coordonnées du point |\color{green}{P}.| |
|
|\begin{align} y &= \color{blue}{20{,}33} x + \color{red}{7{,}503} \\ y &= \color{blue}{20{,}33} (20) + \color{red}{7{,}503} \\ y &= 414{,}103 \end{align}| |
Étant donné qu'on souhaite connaitre la hauteur des arbres après |20| ans, on substitue |x| par |20.| |
|
Après |20| ans, les arbres auront une hauteur d'environ |414{,}103\ \text{cm}.| Ainsi, les premiers balcons doivent être d'une hauteur minimale de |414{,}103\ \text{cm}.| |
|
Même si la situation et les données sont les mêmes, il est normal que la réponse finale varie selon la méthode utilisée (Méthode médiane-médiane ou Méthode de Mayer).
Puisque ce sont des méthodes qui servent à estimer et non à prédire les résultats avec certitude, il se peut qu'il y ait une différence entre les deux résultats.
À voir aussi
Pour trouver l'équation de la droite de régression selon la méthode de Mayer, on peut se fier aux étapes suivantes :
-
Mettre les couples en ordre croissant selon la valeur en |x.|
-
Séparer les couples en deux groupes égaux, si possible.
-
Calculer les points moyens |(P_1| et |P_2)| de chacun des groupes.
-
Utiliser ces points moyens pour trouver la valeur de la pente |(a)| et de la valeur initiale |(b).|
-
Écrire l'équation de la droite de régression sous la forme |y = ax + b.|
Avant de construire une nouvelle tour à condo et d'en faire l'emménagement paysager, on s'intéresse à la hauteur des arbres afin qu'ils ne cachent pas la vue aux futurs résidents pour au moins les 20 prochaines années. Pour estimer la hauteur de ces derniers, on utilise la table de valeurs suivante :
À l'aide de ces information, détermine à quelle hauteur devrait se situer les premiers balcons afin que la vue ne soit pas obstruée par les arbres.
| CALCULS | EXPLICATIONS |
|---|---|
| |
Il faut d'abord placer les couples en ordre croissant selon la valeur de la variable indépendante, sans défaire les couples initiaux. |
| |
Si possible, séparer la distribution en deux groupes égaux. |
|
|\begin{align} P_1 &= \left(\dfrac{\color{red}{1+1+... +2+2}}{7}, \dfrac{\color{blue}{21+23+...+42+54}}{7}\right) \\ &\approx (\color{red}{1{,}43} ; \color{blue}{34{,}29}) \\\\ P_2 &= \left(\dfrac{\color{green}{3+3...+4+4}}{7}, \dfrac{58+59+...+90+97}{7}\right) \\ &\approx (\color{green}{3{,}43} ; 76) \end{align}| |
Calculer les points moyens de chancun des groupes. |
|
|a = \dfrac{\Delta y}{\Delta x} = \dfrac{76 - \color{blue}{34{,}29}}{\color{green}{3{,}43} - \color{red}{1{,}43}} \approx 20{,}86| Ainsi, |y = 20{,}86x + b.| Par substitution des coordonnées de |P_1:| ||\begin{align} y &= 20{,}86x + b \\ 34{,}29 &= 20{,}86 (1{,}43) + b \\ 34{,}29 &= 29{,}83 + b \\ 4{,}46 &= b \end{align}|| Ainsi, |y = 20{,}86x + 4{,}46.| |
Trouver l'équation de la droite de régression sous la forme |y = ax + b| selon les points |P_1| et |P_2.| |
|
|\begin{align} y &= 20{,}86x + 4{,}46 \\ y &= 20{,}86 (20) +4{,}46 \\ y &= 417{,}2 + 4{,}46 \\ y &= 421{,}66 \end{align}| |
Étant donné qu'on souhait connaitre la hauteur des arbres après |20| ans, on substitue |x| par |20.| |
|
Après |20| ans, les arbres auront une hauteur d'environ |421{,}66\ \text{cm}.| Ainsi, les premiers balcons doivent être d'une hauteur minimale de |421{,}66\ \text{cm}.| |
|
Même si la situation et les données sont les mêmes, il est normal que la réponse finale varie selon la méthode utilisée (Méthode médiane-médiane ou Méthode de Mayer).
Puisque ce sont des méthodes qui servent à estimer et non à prédire les résultats avec certitude, il se peut qu'il y ait une différence entre les deux résultats.