Here are the laws and properties of exponents that will be useful for the rest of this section:
-
|\left(\dfrac{a}{b}\right)^{-m} = \left(\dfrac{b}{a}\right)^m|
-
|a^{\frac{m}{n}} = \sqrt[n]{a^m}|
-
|a^m \times a^n = a ^{m+n}|
-
|\displaystyle \frac{a^m}{a^n} = a^{m-n}|
-
|(ab)^m = a^m b^m|
-
|\left(\displaystyle \frac{a}{b}\right)^m = \frac{a^m}{b^m}|
-
|(a^m)^n = a^{m n}|
-
|a^0=1|
Simplify the following expression as much as possible: ||\dfrac{(27 a^3 b)^{\frac{1}{2}}}{27^{\frac{1}{3}}a^3}||
-
Express the coefficients in terms of the same base, if possible ||\begin{align} &\dfrac{(27 a^3 b)^{\frac{1}{2}}}{27^{\frac{1}{3}}a^3} \\ =\ &\dfrac{(3^3 a^3 b)^{\frac{1}{2}}}{(3^{3})^{\frac{1}{3}}a^3} \end{align}||
-
Use the laws and properties of exponents to simplify as much as possible ||\begin{align} &\frac{\sqrt{3^3 a^3 b}}{3^1 a^3} &&\text{Fractional exponent }:a^{^\frac{m}{n}} =\sqrt[n]{a^m} \\ =\ &\dfrac{\sqrt{\color{blue}{3^2} 3^1 \color{red}{a^2} a^1 b}}{3^1 a^3} &&\text{Power of a product }:a^{m+n}=a^ma^n \\ =\ &\dfrac{\color{blue}{3} \color{red}{a} \sqrt{3ab}}{3 a^3} &&\text{Factoring of a square root}:\sqrt[n]{a^nb}=a\sqrt[n]{b}\\ =\ &\dfrac{\sqrt{3ab}}{a^2} &&\text{Simplification }:\dfrac{3a}{3a^3} = \dfrac{\cancel{3}}{\cancel{3}a^{3-1}} = \dfrac{1}{a^2} \end{align}||
The simplified expression is |\dfrac{\sqrt{3ab}}{a^2}.|
See also
In general, the law of multiplication of radicals is used to factor: |\sqrt { a \times b} = \sqrt{a} \times \sqrt{b}.|
Before performing the calculation, it is necessary to:
-
Decompose the radicand into a product of factors, one of which is a square number
-
Transform the root of a product into a product of roots |(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b})|
-
Calculate the root of the square number
Determine the simplified value of the following root : ||\sqrt{45}||
| CALCULATIONS | EXPLANATIONS |
|---|---|
|
|\sqrt{45} = \sqrt{\color{blue}{9} \times 5}| |
Factor the radicand with a square number. |
|
|\sqrt {\color{blue}{9} \times 5}| |
Use the law of the product of radicals |(\sqrt{a \times b} = \sqrt{a} \times \sqrt{b})| |
|
|\sqrt {\color{blue}{9}} \times \sqrt {5}| |
Calculate the square roots |
|
Thus, |\sqrt{45} = 3 \sqrt{5}| |
|
See also
The following are the laws of logarithms that are important to master:
-
|\log_c(M N) = \log_c M + \log_c N|
-
|\log_{c}\left(\dfrac{M}{N}\right)=\log_{c}M-log_{c}N|
-
|\log_{\frac{_{1}}{c}}M=-\log_{c}M|
-
|\log_c M^n = n \log_c M|
-
|\log_a b = \dfrac{\log_c b}{\log_c a}|
Simplify the following expression using the laws of logarithms: ||\log_4 6x^2 + \log_4 9xy - \log_4 2y||
Use the laws of logarithms with those that have the same base. ||\begin{align} &\color{blue}{\log_4 6x^2 + \log_4 9xy} - \log_4 2y \\ =\ &\color{blue}{\log_4 (6x^2 \times 9xy)} - \log_4 2y\\ =\ &\color{red}{\log_4 54x^3y - \log_4 2y}\\ =\ &\color{red}{\log_4 \left(\dfrac{54x^3y}{2y}\right)}\\ =\ &\log_4 27x^3 \\ =\ &\log_4 3^3 x^3\\ =\ &\log_4 (3x)^3\\ =\ &3 \log_4 3x \end{align}||
Thus, the simplified expression is |3 \log_4 3x.|
See also
Here is a brief overview of the properties of absolute values that are important to keep in mind:
-
By definition, |{\mid}x{\mid} = \max\{-x, x\}|
-
|{\mid}a{\mid} = {\mid}-a{\mid}|
-
|{\mid}a \ b{\mid} = {\mid}a{\mid} {\mid}b{\mid}|
-
|\vert\dfrac{a}{b}\vert = \dfrac{\mid a \mid}{\mid b \mid}|
Factor the following algebraic expression: ||{\mid}-4x+8{\mid}|| of the form |a {\mid}x \pm h{\mid}.|
-
Factor out a common factor so that the coefficient of |x = 1| ||{\mid}-4x+8{\mid} = {\mid}-4(x-2){\mid}||
-
Use the property that refers to the multiplication of absolute values ||\phantom{{\mid}-4x+8{\mid}} = {\mid}-4{\mid}\ {\mid}x-2{\mid}||
-
Calculate the value of |{\mid}-4{\mid}| ||\phantom{{\mid}-4x+8{\mid}} = 4 {\mid}x-2{\mid}||
Thus, the factored expression is |4 {\mid}x-2{\mid}.|
See also
|f(x) = a (c) ^{bx} + k|
where
|b = | compounding frequency
|k = | asymptote
| c = 1 \pm| percentage change as a decimal number
When an investment is made with a banking institution, the return is generally evaluated according to an exponential function. However, a minimum amount of investment is required to benefit from more advantageous rates.
So, after how many years does an initial investment of $5 000, compounded every two years at an interest rate of 5% with a minimum investment of $3 000, return at least $8 000?
-
Find the value of parameter |k|
Minimum investment required | = $3\ 000 \Rightarrow 3\ 000 = k|
-
Find the value of parameter |c| ||\begin{align} c &= 1 \pm 5\ \% \\ &= 1 + 0{.}05 \\ &= 1{.}05 \\\\ \Rightarrow\ f(x) &= a (1{.}05)^{bx}+ 3\ 000 \end{align}||
-
Find the value of parameter |b| depending on the context
Compounded every two years |\Rightarrow b = \dfrac{1}{2}|
Thus, |f(x) = a (1{.}05)^{\frac{1}{2}x}+ 3\ 000| -
Replace |(x,y)| by the given initial value: |(0,5\ 000)| ||\begin{align} 5\ 000 &= a(1{.}05)^{\frac{1}{2}(0)}+3\ 000 \\ 5\ 000 &= a (1) + 3\ 000 \\ 2\ 000 &= a \end{align}||
-
Replace |f(x)| with |$8\ 000| ||\begin{align} 8\ 000 &= 2\ 000 (1{.}05)^{\frac{1}{2}x}+3\ 000 \\ 2{.}5 &= 1{.}05^{\frac{1}{2}x} \\ \Rightarrow\ \log_{1{.}05}2{.}5 &= \dfrac{1}{2}x \\ 18{.}78 &\approx \dfrac{1}{2}x \\ 37{.}56 &\approx x \end{align}||
Answer: The amount invested will earn at least |$8\ 000| after about |37{.}56| years.
To solve an inequality related to this model, begin by following the same steps while adding one of these steps:
-
Sketch a graph of the situation
-
Check the inequality using a point
The solution set of an inequality is directly related to the equation associated with it.
See also
|f(x) = a \log_c (b(x-h))|
where
|\dfrac{1}{b} + h =| the zero of the function
|h = | the asymptote of the function
According to the function graphed, what will be the value of the x-coordinate if the value of the y-coordinate is 3?
-
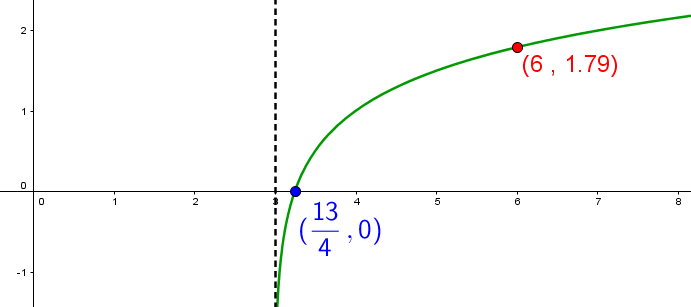
Find the value of |h| according to the vertical asymptote ||h = 3||
-
Use the zero of the function to find the value of the parameter |b| ||\begin{align} \color{blue}{\text{Zero function}} &= \dfrac{1}{b} + h \\ \color{blue}{\dfrac{13}{4}} &= \dfrac{1}{b} + 3 \\ \dfrac{1}{4} &= \frac{1}{b} \\ b &= 4 \end{align}||
-
Find the value of the parameter |c| using the coordinates of the point |\color{red}{(6 , 1{.}79)}| ||\begin{align} \color{red}{1{.}79} &= \log_c(4(\color{red}{6}-3)) \\ \color{red}{1{.}79} &= \log_c(12) \\ c^{1{.}79} &= 12 \\ c &= 4 \end{align}||Thus, |f(x)=\log_4\big(4(x-3)\big)|
-
Replace |f(x)| by 3 ||\begin{align} 3 &= \log_4\big(4(x-3)\big) \\ 4^3 &= 4(x-3) \\ 19 &= x \end{align}||
Answer: When |y= 3,| |x = 19.|
To solve an inequality related to this model, begin by following the same steps while adding one of these steps:
-
Sketch a graph of the situation
-
Check the inequality using a point
The solution set of an inequality is directly related to the equation associated with it.
See also
|f(x) = a \sqrt{b(x-h)} + k|
where
|(h,k) = | coordinates of the vertex,
|b = | generally |\pm 1| and
signs |a| and |b| depend on the orientation of the curve.
An amateur ornithologist watches a bird take flight from a branch that is three metres above the ground. In addition, the bird’s trajectory follows the following model:
Knowing that it is still possible to observe the bird when it reaches an altitude of 50 m, what will be the horizontal distance separating the ornithologist from the bird at that precise time?
-
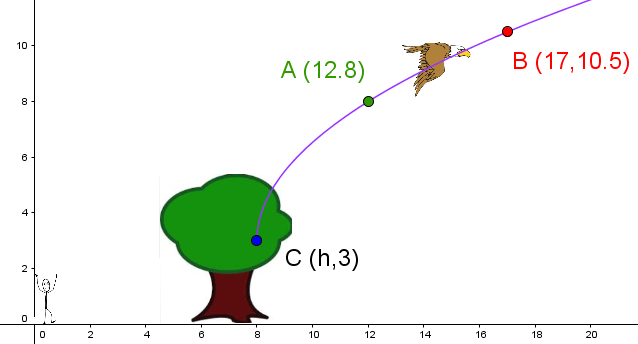
Determine the model to use ||f(x) = \pm a \sqrt{\pm 1(x-h)} + k||
-
Determine the sign of |a| and |b| according to the orientation of the graph
Both are positive. ||\begin{align} f(x) &= a \sqrt{1(x-h)} + k \\ \Rightarrow\ f(x) &= a \sqrt{x-h} + k \end{align}|| -
Create two equations with the points provided ||\begin{align} \color{green}{8} &= a \sqrt{\color{green}{12} - h} + 3 \\ 25 &= a^2 (\color{green}{12}- h) \\ \dfrac{25}{\color{green}{12}-h} &=a^2 \\\\ \color{red}{10{.}5} &= a \sqrt{\color{red}{17} - h} + 3 \\ 56{.}25 &= a^2 (\color{red}{17}- h) \\ \dfrac{56{.}25}{\color{red}{17}-h} &= a^2 \end{align}||
-
Compare the two values of |a^2| ||\begin{align} \dfrac{56{.}25}{17 - h} &= \dfrac{25}{12-h} \\ 56{.}25 (12-h) &= 25 (17-h) \\ 675 - 56{.}25h &= 425 - 25h \\ 250 &= 31{.}25h \\ 8 &= h \end{align}||
-
Use one of the points to find the value of |a| ||\begin{align} \color{green}{f(x)} &= a \sqrt{\color{green}{x}-8} + 3 \\ \color{green}{8} &= a \sqrt{\color{green}{12} - 8} + 3 \\ 8 &= a (2) + 3 \\ 2{.}5 &= a \end{align}||
-
Replace |f(x)| with |50| since it is the altitude at which the bird is flying ||\begin{align} f(x) &= 2{.}5 \sqrt{x-8} + 3 \\ 50 &= 2{.}5 \sqrt{x-8}+3 \\ 18{.}8 &= \sqrt{x-8} \\ 353{.}44 &= x-8 \\ 361{.}44 &= x \end{align}||
Answer: The bird will be at a horizontal distance of |361{.}44| metres.
To solve an inequality related to this model, begin by following the same steps while adding one of these steps:
-
Sketch a graph of the situation
-
Check the inequality using a point
The solution set of an inequality is directly related to the equation associated with it.
See also
In standard form: |f(x) = \displaystyle \frac{a}{b(x-h)} + k|
In general form: |f(x) = \displaystyle \frac{ax+b}{cx+\ d}|
Based on the information available in the graph, determine the x-coordinate of point |\color{red}{B}.|
-
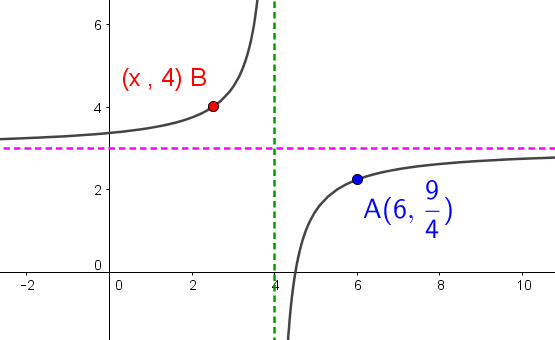
Determine the values of |(h,k)| according to the |h=| vertical asymptote and the |k=| horizontal asymptote ||\color{green}{h = 4} \\ \color{fuchsia}{k=3}||
-
Find the parameter value |a| using the coordinate of the point |\color{blue}{A(6, \dfrac{9}{4})}| ||\begin{align} f(x) &= \dfrac{a}{x-\color{green}{h}}+\color{fuchsia}{k} \\\\ \color{blue}{\dfrac{9}{4}} &= \dfrac{a}{\color{blue}{6}-\color{green}{4}}+\color{fuchsia}{3} \\\\ -\dfrac{3}{4} &= \dfrac{a}{2} \\\\ -\dfrac{3}{2} &= a \end{align}||
-
Replace |f(x)| by the y-coordinate of the point |\color{red}{B}| and isolate |x| ||\begin{align} \color{red}{4} &= \dfrac{-3}{2(\color{red}{x}-\color{green}{4})}+\color{fuchsia}{3} \\ 1 &= \dfrac{-3}{2(\color{red}{x}-\color{green}{4})} \\ 2(\color{red}{x}-\color{green}{4}) &= -3 \\ \color{red}{x} &= \color{red}{\dfrac{5}{2}} \end{align}||
Answer: The coordinates of point |\color{red}{B}| are |\color{red}{\left(\dfrac{5}{2} , 4\right)}.|
To solve an inequality related to this model, begin by following the same steps while adding one of these steps:
-
Sketch a graph of the situation
-
Check the inequality using a point
The solution set of an inequality is directly related to the equation associated with it.
See also
|f(x) = a {\mid}x - h{\mid} + k|
where
|(h,k) =| vertex coordinate
|\pm a =| slope of each straight line forming the function’s graph
What are the values of the following function’s x-coordinate when its y-coordinate is -5?
-
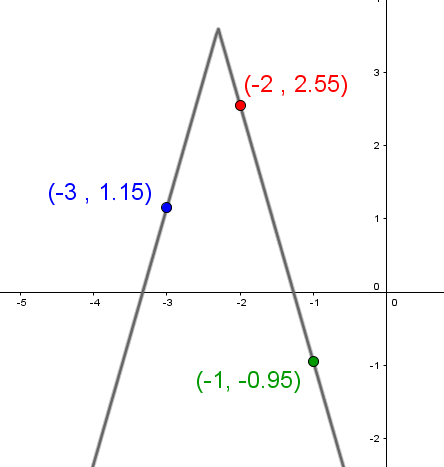
Find the equation of the first branch in the form |\color{fuchsia}{y = a_1x + b_1}| ||\begin{align} a_1 = \dfrac{\Delta y}{\Delta x} &= \dfrac{\color{green}{(-0{.}95)}-\color{red}{2{.}55}}{\color{green}{(-1)} - \color{red}{(-2)}} \\ &= -3{.}5 \\\\ \Rightarrow\ y &= -3{.}5 x + b_1 \\ \color{red}{2{.}55} &= -3{.}5 \color{red}{(-2)} + b_1 \\ -4{.}45 &= b_1 \end{align}||Thereby, |\color{fuchsia}{y = -3{.}5x - 4{.}45}.|
-
Determine the equation of the second branch in the form |\color{orange}{y=a_2x + b_2}| with |a_2 = | opposite of |a_1| ||\begin{align} y &= 3{.}5x + b_2 \\ \color{blue}{1{.}15} &= 3{.}5 \color{blue}{(-3)} + b_2 \\ 11{.}65 &= b_2 \end{align}||Thereby, |\color{orange}{y = 3{.}5x + 11{.}65}.|
-
Determine, by comparison, the point of intersection of the two straight lines corresponding to the function’s vertex |(h,k)| ||\begin{align} \color{fuchsia}{-3{.}5x - 4{,}45} &= \color{orange}{3{.}5x+11{.}65} \\ -16{.}1 &= 7x \\ -2{.}3 &= x \\\\ \color{fuchsia}{y} &= \color{fuchsia}{-3{.}5x -4{.}45} \\ \color{fuchsia}{y} &= \color{fuchsia}{-3{.}5} (-2{.}3) \color{fuchsia}{- 4{.}45} \\ y &= 3{.}6 \end{align}||
-
Determine the rule of the absolute value function
Since the graph is open downward, the parameter |a| of the absolute value function equation will be negative.||\begin{align} f(x) &= a {\mid}x-h{\mid} + k \\\\ f(x) &= -3{.}5 {\mid}x - (-2{.}3){\mid} + 3{.}6 \end{align}|| -
Replace |f(x)| by the given value, thus |-5| ||\begin{align} -5 &= -3{.}5 {\mid}x+2{.}3{\mid} +3{.}6 \\ 2{.}46 &\approx {\mid}x+2{.}3{\mid} \end{align}||According to the definition of the absolute value, the result is the following: ||\begin{align} \color{blue}{2{.}46} &\approx x_1+2{.}3 &&\text{and}\quad \color{red}{-2{.}46} \approx x_2 +2{.}3 \\ \color{blue}{0{.}16} &\approx x_1 &&\text{and}\quad \color{red}{-4{.}76} \approx x_2 \end{align}||
Answer: The values of |x| when |y=-5| are |\color{blue}{0{.}16}| and |\color{red}{-4{.}76}.|
To solve an inequality related to this model, begin by following the same steps while adding one of these steps:
-
Sketch a graph of the situation
-
Check the inequality using a point
The solution set of an inequality is directly related to the equation associated with it.
See also
We can choose from three trigonometric function models depending on the situation:
|f(x) = a \cos (b (x-h)) + k|
|g(x) = a \sin(b (x-h)) + k|
|h(x) = a \tan(b (x-h)) + k|
To keep your dog entertained, you decide to go outside and play his favourite game of “go fetch”. You are standing 10 metres from the house. You always throw the ball 30 metres from you. In addition, you noticed that at this distance, your dog takes 12 seconds to fetch the ball and bring it back to you. Of course, you throw the ball again as soon as he brings it back to you. You do this for five minutes.
However, since your dog is not perfectly trained, you are afraid that he will run away when he is more than 30 metres from the house. Taking this information into account, for how long during the game are you afraid that your dog will run away?
-
Modeling the situation
-
Find the equation for the function ||\begin{align} f(x) &= a \cos(b (x-h)) + k \\\\ (h,k) &= \left(0, \dfrac{40+10}{2}\right) = (0, 25) \\ {\mid}a{\mid} &= \dfrac{40-10}{2} = 15\\ \rightarrow\ a &= -15\ \text{since}\ (h,k)\ \text{is a minimum} \\ b &= \dfrac{2\pi}{12} = \dfrac{\pi}{6} \\\\ \Rightarrow\ f(x) &= -15 \cos \left(\frac{\pi}{6}x\right) + 25\end{align}||
-
Replace |f(x)| by 30 to determine the time interval when the dog is more than 30 metres from the house ||\begin{align} 30 &= -15 \cos \left(\dfrac{\pi}{6}x\right) + 25 \\ -\dfrac{1}{3} &= \cos \left(\frac{\pi}{6}x\right)\end{align}|| Since |\cos^{-1} \left(-\frac{1}{3}\right) \approx 1{.}911,| thus: ||\begin{align} 1{.}911 &= \dfrac{\pi}{6}x_1 &&\text{and}\qquad 2\pi - 1{.}911 = \dfrac{\pi}{6}x_2 \\ 3{.}65 &\approx x_1 &&\text{and}\qquad 8{.}35 \approx x_2 \end{align}|| An interval has a length of |8{.}35 - 3{.}65 = 4{.}7| seconds.
In addition, there are a total of 25 intervals. ||\begin{align} &5\ \text{min} \div 12 \ \text{sec/interval} \\ =\ &300\ \text{sec} \div 12\ \text{sec/interval} \\ =\ &25\ \text{intervals} \end{align}||
Answer: You are afraid that your dog will run away for a total of |25 \times 4{.}7 = 117{.}5 \ \text{sec}.|
To solve an inequality related to this model, begin by following the same steps while adding one of these steps:
-
Sketch a graph of the situation
-
Check the inequality using a point
The solution set of an inequality is directly related to the equation associated with it.
See also
Before solving this kind of equation, it is important to simplify them as much as possible using the different trigonometric identities.
What are the values of |x| which satisfy the following equation: ||3 \sin^2x + \sec x - 0{.}48 = \dfrac{1}{\cos x}||
-
Use basic identity |\dfrac{1}{\cos x} = \sec x| ||\begin{align} \dfrac{1}{\cos x} &= 3 \sin^2x + \sec x - 0{,}48 \\ \sec x &= 3 \sin^2x + \sec x - 0{.}48 \\ 0 &= 3 \sin^2x - 0{.}48 \end{align}||
-
Factor out a common factor ||0 = 3 (\sin^2x - 0{.}16)||
-
Factor using the difference of squares ||\begin{align} 0 &= 3 (\sin x - 0{.}4)(\sin x + 0{.}4) \\ 0 &= \color{green}{(\sin x - 0{.}4)} \color{red}{(\sin x + 0{.}4)} \end{align}||
-
Find the two possible values of |x| ||\begin{align} \color{green}{\sin x -0{.}4} &= 0 &&\text{or} &\color{red}{\sin x +0{.}4} &= 0 \\ \color{green}{\sin x} &= \color{green}{0{.}4} &&\text{or} &\color{red}{\sin x} &= \color{red}{-0{.}4} \\ \color{green}{x} &\approx \color{green}{0{.}41} &&\text{or} &\color{red}{x} &\approx \color{red}{-0{.}41} \end{align}||
Answer: The values that respect the equality are: |x = \{\color{green}{0{.}41}+ 2\pi n ; \color{red}{-0{.}41}+ 2 \pi n\}| or |n \in \mathbb{Z}|
See also
To perform operations on functions, we use the same concepts as the ones discussed for the simplification of algebraic expressions:
Addition and subtraction
On the coefficients of like terms
Multiplication and division
On the coefficients of all the terms while respecting the laws of exponents
Speculating on the stock market is a real passion for some investors. To try to predict the values of different stocks and the potential profits, they use different graphs and then associate them with mathematical models. To study a certain foreign company, we can use the following functions to model the different variables that influence the final return on each share:
Number of shares on the market: |f(x) = 10x - 500|
Profit from a share: |g(x) = -x^2+160x - 6\ 400|
Number of shareholders: |h(x)= -2x^2 + 260x - 8\ 000|
where |x =| number of years since its creation
What function could be used to determine the average profit obtained by each shareholder?
-
Create an equation that answers the question ||\begin{align} \text{Average profit} &=\ \dfrac{\color{red}{\text{Number of shares}} \times \color{green}{\text{Profit per share}}}{\color{blue}{\text{Number of shareholders}}} \\ &=\ \dfrac{\color{red}{f(x)} \times \color{green}{g(x)}}{\color{blue}{h(x)}} \end{align}||
-
Replace each element by the function it models ||\phantom{\text{Average profit}} =\ \dfrac{\color{red}{(10x-500)} \color{green}{(-x^2+160x-6\ 400)}}{\color{blue}{-2x^2+260x-8\ 000}}||
-
Factor each of the functions so everything is expressed in terms of multiplications and divisions ||\phantom{\text{Average profit}} = \dfrac{\color{red}{10 (x-50)} \color{green}{\big(-(x-80)(x-80)\big)}}{\color{blue}{-2(x-50) (x-80)}}||
-
Simplify ||\begin{align} \phantom{\text{Average profit}} &= \dfrac{-10 \cancel{(x-50)} \cancel{(x-80)}(x-80)}{-2\cancel{(x-50)} (x-80) } \\ &= 5 (x-80) \end{align}||
Answer: Using the information currently available, the average profit is represented by the function |i(x) = 5 (x-80).|
See also
The composition of functions is written |g \circ f = g\big(f(x)\big)|
|g \circ f| can be read as "g composite f".
To determine their budget for the following year, the Alloprof administration committee looked at the production costs of the virtual library files. They used two functions:
Function f : |t = \dfrac{5}{4} n|
Function g : |s = 124t + 2\ 000|
where |n = | number of files produced, |t=| the number of hours worked, and |s = | salary (in $) to be paid to employees.
Model this situation using a single function and then determine the total number of concept sheets that can be made with a budget of $13 625.
-
Model the situation using the composition of functions ||\begin{align} s &= g \circ f \\&= \color{red}{g\big(}\color{blue}{f(n)}\color{red}{\big)} \\ &= \color{red}{124}\color{blue}{\left(\frac{5}{4} n\right)} \color{red}{+ 2\ 000} \\ \Rightarrow\ s &= 155 n + 2\ 000 \end{align}||
-
Replace |s| with |13\ 625| and isolate |n| ||\begin{align} 13\ 625 &= 155 n + 2\ 000 \\ 11\ 625 &= 155n\\ 75 &= n \end{align}||
Answer: With $13 625, it would be possible to produce a total of 75 new concept sheets.
See also
Generally, an optimization problem can be solved by following these steps:
-
Identify variables and unknowns.
-
Determine the equation of the function to be optimized as well as the target objective (minimize or maximize).
-
Create a system of inequalities.
-
Sketch the polygon of constraints.
-
Determine the coordinates of each of the polygon’s vertices.
-
Substitute the coordinates of each vertex in the function to be optimized to determine the optimal solution(s).
-
Give a complete answer taking into account the context.
In order to maximize his business’ profits, the owner wants to know how many jackets and shirts he must sell each week. Due to production constraints, he knows that the maximum number of shirts corresponds to the difference between 21 and quadruple the number of jackets. For transportation reasons, the number of jackets must be greater than or equal to the difference between eight and three times the number of shirts. Finally, the difference between triple the number of jackets and double the number of shirts must be at least two.
Knowing that each jacket sold brings in a profit of $32 and the profit associated with selling a shirt is $17, what is the maximum weekly profit the business owner can expect to make?
| CALCULATIONS | EXPLANATIONS |
|---|---|
|
|x=| number of jackets |y=| number of shirts |
Identify the variables. The association of |x| and |y| is usually done randomly. |
|
|Z=32x+17y| |
Find the function to optimize. |
|
|\begin{align} &\color{blue}{y \le 21 - 4x} \\ &\color{green}{x \ge 8 - 3y} \\ &\color{red}{3x - 2y \ge 2} \\ &x \ge 0 \\ &y \ge 0 \end{align}| |
Identify inequalities without forgetting the non-negative constraints. |
|
|\begin{align} &\color{blue}{y \le 21 - 4x} \\ &\color{green}{y \ge -\frac{1}{3}x + \frac{8}{3}} \\ &\color{red}{y \le \frac{3}{2}x - 1} \end{align}| |
Isolate the |y| in each of the inequalities in order to write them in the functional form. |
 |
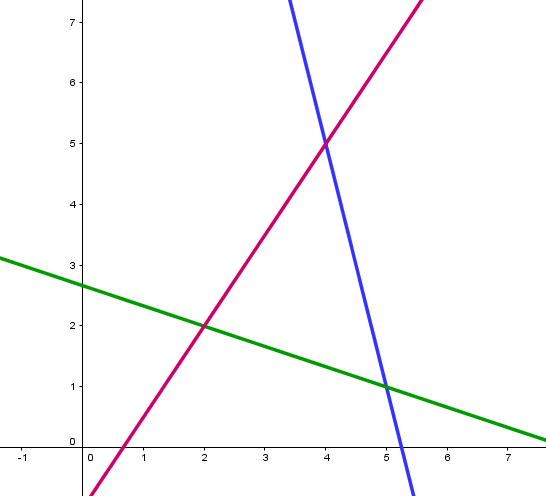Draw the straight line-boundaries of each of the inequalities in a Cartesian plane. |
 |
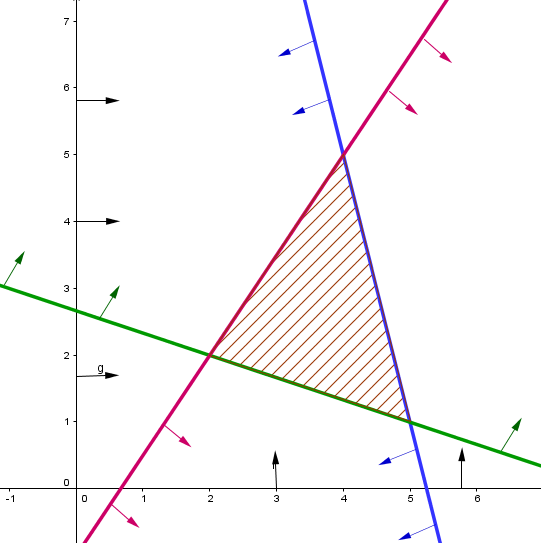Find the polygon of constraints that respects all of the inequalities. |
 |
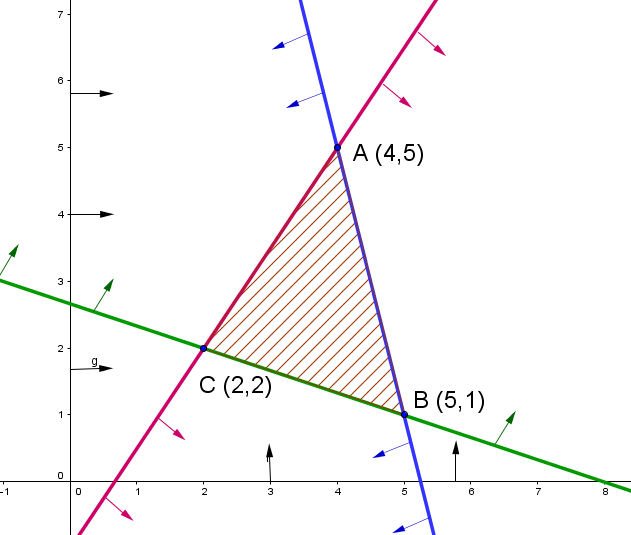Find the coordinates for each of the vertices using the comparison, substitution, or elimination method. |
|
According to the point |A (4.5):| According to the point |B (5.1):| According to the point |C (2.2):| |
Calculate the profit for each point by using the rule of the function to optimize. |
|
To maximize his profit, the owner should sell 4 jackets and 5 shirts for a maximum profit of $213. |
|
See also
A radian angle measurement corresponds to the central angle formed by an arc of a circle with a measurement equivalent to the radius.
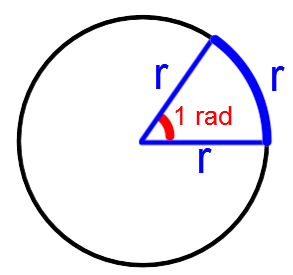
In addition, the following proportion can be used to transform a measurement in degrees to a measurement in radians and vice versa: ||\displaystyle \frac{\text{angle measurement in degrees}}{180^\circ} = \frac{\text{angle measurement in radians}}{\pi\ rad}||
If an angle measures |\color{red}{227^\circ},| what is its measurement in radians?
| CALCULATIONS | JUSTIFICATIONS |
|---|---|
|
|\color{white}{\Rightarrow}\displaystyle \frac{\text{angle measurement in degrees}}{180^\circ} = \frac{\text{angle measurement in radians}}{\pi\ rad}| |\Rightarrow \displaystyle \frac{\color{red}{227^\circ}}{180^\circ} = \frac{\text{angle measurement in radians}}{\pi\ rad}| |
Use the proportion identified above. |
|
|\Rightarrow \color{red}{227^\circ} \times \pi \div 180^\circ = \text{angle measurement in radians}| |\color{white}{\Rightarrow 227^\circ \times \pi}3{.}96 \ rad = \text{angle measurement in radians}| |
Solve using cross multiplication. |
|
The angle at the centre measures |3{.}96 \ rad.| |
|
|\tan \theta = \displaystyle \frac{\sin \theta}{\cos \theta}|
|\cot \theta = \displaystyle \frac{\cos\theta}{\sin\theta}|
|\csc \theta = \displaystyle \frac{1}{\sin \theta}|
|\sec \theta = \displaystyle \frac{1}{\cos \theta}|
|\sin ^2 + \cos ^2 = 1|
|1 + \cot ^2 = \csc ^2|
|\tan ^2 + 1 = \sec ^2|
Prove the following identity: ||\sec \theta - \cos \theta = \tan \theta \sin \theta||
| CALCULATIONS | JUSTIFICATIONS |
|---|---|
|
|\sec \theta - \cos \theta = \dfrac{1}{\cos \theta} - \cos \theta| |
Transform terms into |\sin \theta| and |\cos \theta.| |
|
|\begin{align} \phantom{\sec \theta - \cos \theta} &= \dfrac{1}{\cos \theta} - \frac{\cos ^2 \theta}{\cos \theta}\\ &= \dfrac{1 - \cos ^2 \theta}{\cos \theta} \end{align}| |
Find a common denominator to subtract. |
|
|\phantom{\sec \theta - \cos \theta} = \dfrac{\sin ^2 \theta}{\cos \theta}| |
Use |\sin ^2 \theta + \cos ^2 \theta = 1 \Rightarrow \sin ^2 \theta = 1 - \cos ^2 \theta.| |
|
|\phantom{\sec \theta - \cos \theta} = \dfrac{\color{blue}{\sin \theta} \ \sin \theta}{\color{blue}{\cos \theta}}| |
Decompose |\sin ^2 \theta = \sin \theta \ \sin \theta.| |
|
|\phantom{\sec \theta - \cos \theta} = \color{blue}{\tan \theta} \ \sin \theta| |
Use |\displaystyle \frac{\sin \theta}{\cos \theta} = \tan \theta.| |
|
The identity is correct, since we have obtained what was indicated at the start. |
|
See also
It is important to master the following vocabulary to fully understand the concept of vectors:
-
The orientation of a vector: is represented by a direction (arrow) and an angle (inclination of a measurement in degrees).
-
The direction of a vector: is always calculated along the positive x-axis, going in a counterclockwise direction.
-
The norm of a vector: is the magnitude or length of the vector obtained by trigonometric ratios or by the Pythagorean Theorem.
-
The work done: is the effort made to move any mass. It is generally measured in Joules.
In a Cartesian plane, draw |\color{red}{\overrightarrow u} = (-3, 8)| and then determine its norm and direction.
| CALCULATIONS | JUSTIFICATIONS |
|---|---|
 |
Use the vector’s components starting from the origin of the Cartesian plane. |
 |
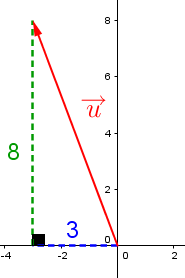Draw a right triangle to determine the norm: ||\begin{align} \mid\mid \color{red}{\overrightarrow u} \mid \mid &= \sqrt{\color{blue}{3}^2 + \color{green}{8}^2} \\ &\approx 8{.}54 \end{align}|| |
 |
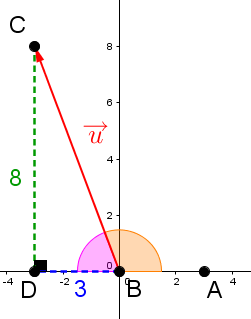Use trigonometric ratios to find the angle measurement associated with the orientation of |\color{red}{\overrightarrow u}| ||\begin{align} \text{Orientation of}\ \color{red}{\overrightarrow u} &= \color{orange}{m\angle ABC} \\ &= 180^\circ - \color{fuchsia}{m\angle DBC} \\ &= 180^\circ - \tan^{-1} \left(\frac{\color{green}{8}}{\color{blue}{3}}\right) \\ &\approx 180^\circ - 69 ^\circ \\ &\approx 111^\circ \end{align}|| |
|
Thus, |\mid \mid \color{red}{\overrightarrow u} \mid \mid\ \approx 8{.}54| and its orientation is approximately |111^\circ.| |
|
See also
To navigate the various operations on vectors, it is important to clearly define the following concepts:
Addition and subtraction
If |\color{blue}{\overrightarrow u = (a,b)}| and |\color{red}{\overrightarrow v = (c,d)}| , thus |\color{blue}{\overrightarrow u} + \color{blue}{\overrightarrow v} = (\color{blue}{a} + \color{red}{c}, \color{blue}{b}+ \color{red}{d}) |
Multiplication of a vector by a scalar
If |\overrightarrow u = (\color{blue}{a}, \color{red}{b})| and |k| is a scalar, then |k \overrightarrow u = (k \color{blue}{a}, k \color{red}{b})|
The scalar product
If |\color{blue}{\overrightarrow u = (a,b)}| and |\color{red}{\overrightarrow v = (c,d)}|, thus |\color{blue}{\overrightarrow u} \cdot \color{red}{\overrightarrow v} = \color{blue}{a}\color{red}{c}+ \color{blue}{b}\color{red}{d}|
Linear combination of two vectors
Given |\color{blue}{\overrightarrow u}| and |\color{red}{\overrightarrow v}| , it is possible to express |\color{green}{\overrightarrow w}| as a linear combination knowing |\color{green}{\overrightarrow w} = k_1 \color{blue}{\overrightarrow u} + k_2 \color{red}{\overrightarrow v}| and |\{k_1,k_2\} \in \mathbb{R}.|
Determine the values of the scalars |\{k_1,k_2\}| given that |\color{blue}{\overrightarrow w = (4,-12)}| is the result of a linear combination of |\color{red}{\overrightarrow u = (-1,4)}| and |\color{green}{\overrightarrow v = (2,5)}.|
| CALCULATIONS | JUSTIFICATIONS |
|---|---|
|
|\begin{align} \color{blue}{\overrightarrow w} &= k_1 \color{red}{\overrightarrow u} + k_2 \color{green}{\overrightarrow v} \\ \color{blue}{(4,-12)} &= k_1 \color{red}{(-1,4)} + k_2 \color{green}{(2,5)}\end{align}| |\Rightarrow\begin{cases}\color{blue}{\ \ \ \ \ 4} = k_1 \color{red}{(-1)} + k_2 (\color{green}{2})\\\color{blue}{-12} = k_1 (\color{red}{4}) + k_2 (\color{green}{5})\end{cases}| |
Create two equations using the definition of linear combination, one for the component in |x| and the other for the component in |y|. |
|
|\begin{align} \color{blue}{-16} &= \color{red}{4}k_1\color{green}{-8}k_2 \\ |\begin{align} \color{blue}{-12} &=\color{red}{4}k_1 +\color{green}{5}\left(\color{fuchsia}{\dfrac{4}{13}}\right) \\ \color{orange}{-\dfrac{44}{13}} &= \color{orange}{k_1} \end{align}| |
Solve the system of equations with the elimination method by multiplying the first equation by |-4.| |
|
Thus, |\color{blue}{\overrightarrow w} = \color{orange}{-\dfrac{44}{13}}\color{red}{\overrightarrow u} + \color{fuchsia}{\dfrac{4}{13}}\color{green}{\overrightarrow v}.| |
|
See also
It is important to master the various procedures associated with operations on vectors, as well as the trigonometric ratios in right triangles, to solve this kind of problem. In general, take the following steps:
-
Illustrate the problem
-
Place the data in the right places on the illustration
-
Find the missing measurements using the Pythagorean relationship or the trigonometric ratios of the right triangle.
After a violent storm, a tree fell on the road leading to Julian's cottage. To clear the roadway, he ties a rope to the bottom of the tree to pull it out of the way.
How much work will Julien have to do to move the tree a distance of 12 m if he exerts a force of |150 \ \text{N}| and the rope he uses forms an angle of |21^\circ| relative to the horizontal (not accounting for friction)?
| CALCULATIONS | JUSTIFICATIONS |
|---|---|
|
|W = \color{red}{150}\cos \color{blue}{21^\circ} \times \color{green}{12}| |
Use this formula to calculate the work: ||W = \color{red}{F}\cos \color{blue}{\theta} \times \color{green}{\Delta x}|| |
|
Julien will have to do a work of |1\ 680 \ J.| |
|
See also
-
|-\overrightarrow {\color{green}{A}\color{red}{B}} = \overrightarrow{\color{red}{B}\color{green}{A}}|
-
|\overrightarrow{\color{green}{A}\color{red}{B}} + \overrightarrow {\color{red}{B}\color{blue}{C}} = \overrightarrow {\color{green}{A}\color{blue}{C}}|
Demonstrate the following: ||(\overrightarrow{AC} + \overrightarrow{BD} - \overrightarrow{AC}) - (\overrightarrow {FG} +\overrightarrow{GE} + \overrightarrow {ED}) = \overrightarrow {BF}||
| CALCULATIONS | JUSTIFICATIONS |
|---|---|
|
|\begin{align} \overrightarrow {BF} &= (\overrightarrow{AC} + \overrightarrow{BD} \color{blue}{- \overrightarrow{AC}}) - (\overrightarrow {FG} +\overrightarrow{GE} + \overrightarrow {ED}) \\ &= (\overrightarrow{AC} + \overrightarrow{BD} \color{blue}{+ \overrightarrow{CA}}) - (\overrightarrow {FG} +\overrightarrow{GE} + \overrightarrow {ED})\end{align}| |
Use the relation 1) on |-\overrightarrow{AC}| of the first bracket. |
|
|\begin{align} &= (\color{blue}{\overrightarrow{AC} + \overrightarrow{CA}} + \overrightarrow{BD}) - (\color{green}{\overrightarrow {FG} +\overrightarrow{GE} + \overrightarrow {ED}}) \\ \phantom{\overrightarrow{BF}} &= (\color{blue}{\overrightarrow{AA}} + \overrightarrow{BD}) - (\color{green}{\overrightarrow {FD}})\end{align}| |
Use relation 2) in each of the brackets. |
|
|\phantom{\overrightarrow{BF}} = \overrightarrow{BD} + \overrightarrow {DF}| |
Use relation 1) on the second bracket and eliminate |\overrightarrow{AA},| because |\overrightarrow{AA} = \overrightarrow 0.| |
|
|\overrightarrow{BF} = \overrightarrow{BF}| |
Use relation 2) on the remaining vectors. |
See also
We calculate |(x, y),| the coordinates of the desired division point, using the following formulas: ||x=x_1+ \dfrac{a}{b} (x_2-x_1)|| ||y=y_1+ \dfrac{a}{b} (y_2-y_1)||
where |(x_1,y_1):| are coordinates of the start of the segment |(x_2,y_2):| are the coordinates of the end of the segment |\dfrac{a}{b}:| is the fraction defining the division of the segment.
Every morning, you have to go to the bus stop and wait for the bus to take you to school. In order for the stop to be centralized for the other students in the neighbourhood, you notice that it divides the street connecting your house to your school at a ratio of 1: 4.
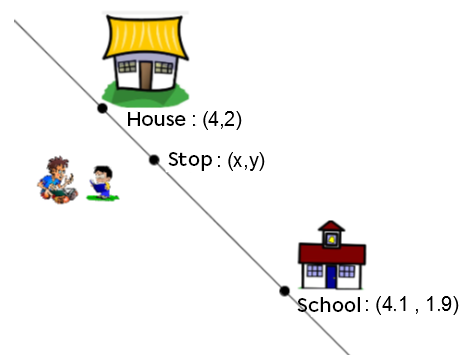
Using the information available, determine the bus stop’s location coordinates.
| CALCULATIONS | EXPLANATION |
|---|---|
|
House |= (\color{blue}{x_1}, \color{red}{y_1}) = (\color{blue}{4}, \color{red}{2})| |
Identify the point of departure and the point of arrival. |
|
|1 : 4 = \dfrac{1}{1+4} = \dfrac{1}{5}| |
Find the fraction |\dfrac{a}{b}| associated with the ratio. |
|
|\begin{align} x &= \color{blue}{x_1} + \dfrac{a}{b} (\color{green}{x_2} - \color{blue}{x_1}) \\ x &= \color{blue}{4} + \frac{1}{5} (\color{green}{4{.}1} - \color{blue}{4}) \\ x &= 4{.}02 \end{align}| |
Substitute the values in the formula and solve the equation to find the coordinate |x| fof the division point. |
|
|\begin{align} y &= \color{red}{y_1} + \dfrac{a}{b} (y_2 - \color{red}{y_1}) \\ y &= \color{red}{2} + \dfrac{1}{5} (1{.}9 - \color{red}{2}) \\ y &= 1{.}98 \end{align}| |
Substitute the values in the formula and solve the equation to find the coordinate |y| of the division point. |
|
Thus, the coordinates of the division point|(x, y)| are |(4{.}02, 1{.}98).| |
|
It is important to differentiate between the two types of notations used to illustrate the portion associated with a division point in order to use the appropriate notation for the formula:
A ratio | = a:b\ \Rightarrow\ \displaystyle \frac{a}{a+b} = | A fraction
See also
For her first fishing trip, Kelsey uses sonar to locate her potential catches. However, she wonders about the range of her sonar. Based on the information presented in the drawing below, determine the area, in |\text{km}^2,| covered by the radar.
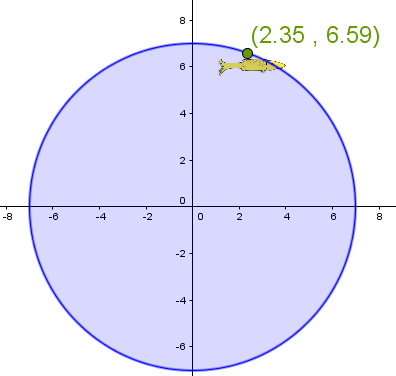
| CALCULATIONS | JUSTIFICATIONS |
|---|---|
|
|\begin{align} r^2 &= \color{green}{x}^2 + \color{green}{y}^2 \\ &=\color{green}{2{.}35}^2 + \color{green}{6{.}59}^2 \\ &\approx 48{.}95 \\ &\approx 6{.}99 \end{align}| |
Use a point to find the radius’s value. |
|
Since the radius measures |6{.}99\ \text{km},| then the area |= \pi \times 6{.}99^2 \approx 153{.}42 \ \text{km}^2.| |
|
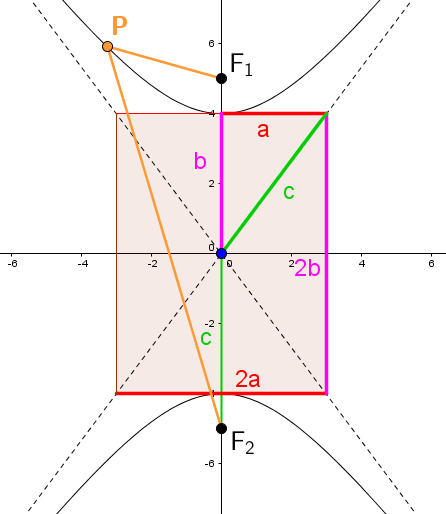
When |\color{green}{b}>\color{red}{a}|
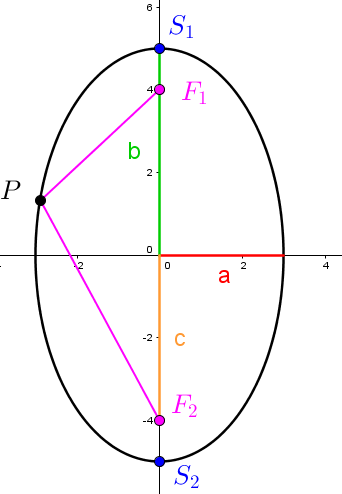
|\overline{\color{fuchsia}{F_1}P} + \overline{\color{fuchsia}{F_2}P} = 2\color{green}{b}|
|\color{red}{a^2}+\color{orange}{c^2} = \color{green}{b^2}|
When |\color{red}{a}>\color{green}{b}|
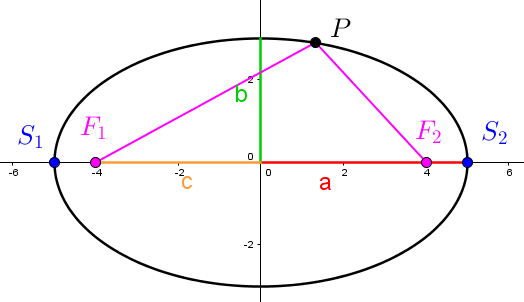
|\overline{\color{fuchsia}{F_1}P} + \overline{\color{fuchsia}{F_2}P} = 2\color{red}{a}|
|\color{green}{b^2}+\color{orange}{c^2} = \color{red}{a^2}|
Having adored her first fishing experience, Kelsey decides to get a magnificent canoe. However, she must determine the exact dimensions of the craft to ensure that she can transport it with her car. To check, she drew the canoe in a Cartesian plane to get the following information:
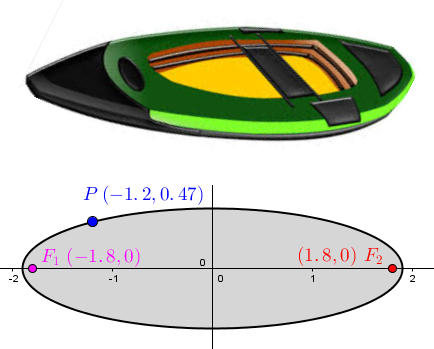
Using the information given, determine the maximum length and width of the canoe.
| CALCULATIONS | JUSTIFICATIONS |
|---|---|
|
|\begin{align} m\overline{\color{fuchsia}{F_1} \color{blue}{P}} &= \sqrt{(\color{fuchsia}{0} - \color{blue}{0{.}47})^2 + (\color{fuchsia}{(-1{.}8)} - \color{blue}{(-1{.}2)})^2} \\ &\approx \sqrt {0{.}58} \\ &\approx 0{.}76 \\\\ m\overline{\color{red}{F_2} \color{blue}{P}} &= \sqrt{(\color{red}{0} - \color{blue}{0{.}47})^2 + (\color{red}{1{.}8} - \color{blue}{(-1{.}2)})^2} \\ &\approx \sqrt {9{.}22} \\ &\approx 3{.}04 \end{align}| |
Find |m\overline{\color{fuchsia}{F_1} \color{blue}{P}}| and |m\overline{\color{red}{F_2} \color{blue}{P}}| . |
|
|\begin{align} 2a &= m\overline{F_1P}+m\overline{F_2P} \\ 2a &= 0{.}76 + 3{.}04 \\ 2a &= 3{.}8 \\ a &= 1{.}9 \end{align}| |
Use the definition of the ellipse to find the measurement of the longest axis. |
|
|\begin{align} 1 &= \dfrac{\color{blue}{x}^2}{a^2} + \dfrac{\color{blue}{y}^2}{b^2} \\ 1 &=\dfrac{\color{blue}{(-1{.}2)}^2}{1{.}9^2} + \dfrac{\color{blue}{0{.}47}^2}{b^2} \\ 1 &= \dfrac{1{.}44}{3{.}61} + \dfrac{0{.}22}{b^2} \\ b^2 &\approx \dfrac{0{.}22}{0{.}60} \\ b &\approx 0{.}61 \end{align}| |
Replace |\color{blue}{(x,y)}| with a point on the ellipse. |
|
Thus, the canoe has a maximum length of |2a = 2 \times 1{.}9 = 3{.}8\ \text{m}| and a maximum width of |2b = 2 \times 0{.}61 = 1{.}22\ \text{m}.| |
|
|\mid m \overline{F_1\color{orange}{P}} - m \overline{F_2\color{orange}{P}}\mid = \color{fuchsia}{2b}|
|\color{red}{a^2}+\color{fuchsia}{b^2}= \color{green}{c^2}|
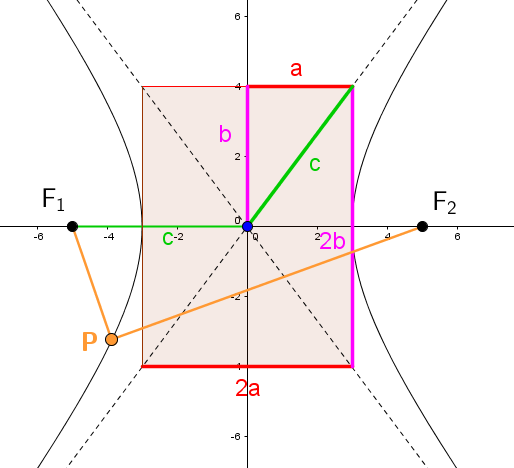
|\mid m \overline{F_1\color{orange}{P}} - m \overline{F_2\color{orange}{P}}\mid = \color{red}{2a}|
|\color{red}{a^2}+\color{fuchsia}{b^2}= \color{green}{c^2}|
Regardless of the orientation of the hyperbola, the rate of change of the asymptotes (dotted lines) is equivalent to |\displaystyle \pm \frac{\color{fuchsia}{b}}{\color{red}{a}}.|
Kelsey decides to paddle in a faster current. To her great dismay, two boats begin to overtake her simultaneously. To avoid capsizing, she must pilot her boat away from the point where two wakes formed by the boats intersect. The situation can be illustrated as follows:
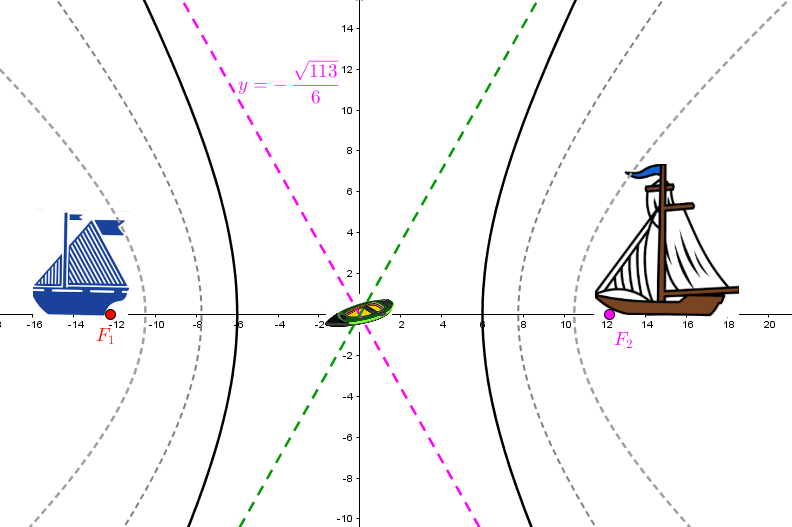
Using the data given, determine the equation associated with the mathematical model enabling Kelsey to better navigate.
| CALCULATIONS | JUSTIFICATIONS |
|---|---|
|
|1 =\displaystyle \frac{x^2}{a^2} - \frac{y^2}{b^2}| |
Determine the shape of the hyperbola equation according to its orientation. |
|
|y = \displaystyle - \frac{\sqrt{113}}{6}| |
Use the equation of asymptotes to find the value of parameters |a| and |b| . |
|
The equation defining the hyperbola of the wakes that are meeting is |
|
See also
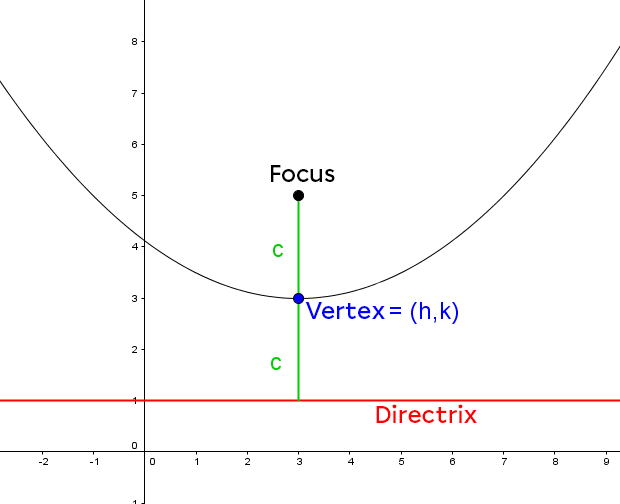
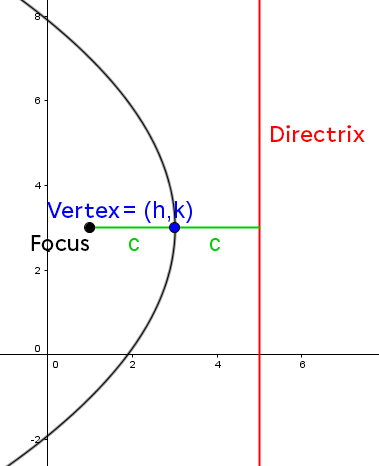
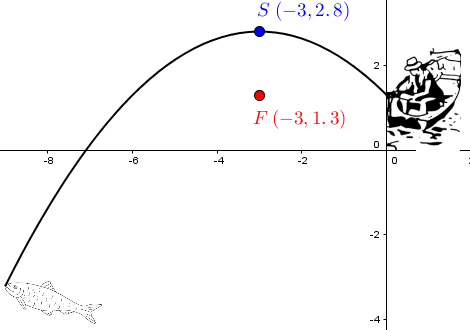
Kelsey has noticed the curvature of her fishing rod when a fish bites the hook is a good indication of the size of the fish. Using her previously purchased sonar, she determines the following information:
Since it is a parabolic shape, Kelsey considers its equation that can model the situation.
| CALCULATIONS | JUSTIFICATIONS |
|---|---|
|
|\begin{align} d(\color{red}{F}, \color{blue}{S}) &= \color{blue}{y_2} - \color{red}{y_1} \\ &= \color{blue}{2{.}8} - \color{red}{1{.}3} \\ &= \color{green}{1{.}5}\end{align}| |
Calculate the distance between |\color{red}{F}| and |\color{blue}{S}.| |
|
|(x-\color{blue}{h})^2 = -4 \color{green}{c} (y-\color{blue}{k})| |
Determine the correct model for the parabola equation. |
|
|\begin{align} \color{green}{c} &= \color{blue}{2{.}8} - \color{red}{1{.}3} \\ &= \color{green}{1{.}5} \end{align}| |
Calculate the value of the parameter |\color{green}{c}| |
|
|(x \color{blue}{+ 3})^2 = -4 \color{green}{(1{.}5)}(y- \color{blue}{2{.}8})| |
Replace the parameters with their respective values. |
|
Finally, Kelsey can model the situation with the equation |(x \color{blue}{+ 3})^2 = -6(y- \color{blue}{2{.}8}).| |
|
See also
A system of equations is generally solved by using the substitution method.
Kelsey is a little tired of fishing and decides to pay for a trip to a region where it is possible to go boating with prehistoric-looking sharks that look like sea dinosaurs. The water is practically clear, so she can easily see them swimming, but she loses sight of them when they pass underneath the boat.
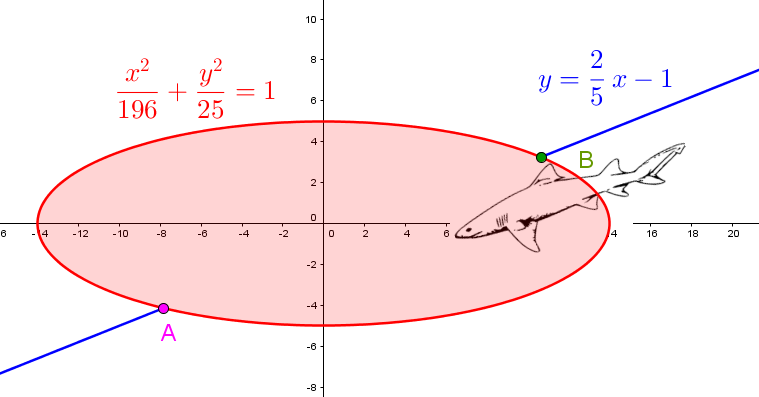
Assuming they are swimming in a straight line at a speed of 5 m/sec, determine how long the sharks are underneath the vessel.
| CALCULATIONS | JUSTIFICATIONS |
|---|---|
|
|\begin{align} \color{red}{1} &= \color{red}{\dfrac{x^2}{196} + \dfrac{y^2}{25} } \\ \color{blue}{y} &= \color{blue}{\dfrac{2}{5}x - 1} \end{align}| |
Determine the equations of the conic and the straight line. |
|
|\color{red}{1 =\dfrac{x^2}{196}} + \dfrac{\left(\color{blue}{\frac{2}{5}x - 1}\right)^2}{\color{red}{25}}| |
Substitute |\color{red}{y}| in the ellipse equation by |\color{blue}{y}| of the linear function. |
|
|\begin{align} 1 &= \dfrac{x^2}{196}+\dfrac{0{.}16x^2-0{.}8x+1}{25} \\ |
Solve the equation to find the values of |\color{fuchsia}{x_1}| and |\color{green}{x_2}.| |
|
|\begin{align} \color{fuchsia}{y_1} &= \color{blue}{\dfrac{2}{5}} \color{fuchsia}{(-7{.}85)} \color{blue}{-1} \\&\approx \color{fuchsia}{-4{.}14} \\\\ \color{green}{y_2} &= \color{blue}{ \dfrac{2}{5}} \color{green}{(10{.}63)} \color{blue}{-1} \\ &\approx \color{green}{3{.}25}\end{align}| |
Calculate the values of |\color{fuchsia}{y_1}| and |\color{green}{y_2}| . |
|
|\begin{align} d(\color{fuchsia}{A}, \color{green}{B}) &= \sqrt{\big(\color{green}{3{.}25} - \color{fuchsia}{(-4{.}14)}\big)^2 + \big(\color{green}{10{.}63} - \color{fuchsia}{(-7{.}85)}\big)^2} \\ &\approx 19{.}90 \ \text{m} \end{align}| |
Calculate the distance between |\color{fuchsia}{A (-7{.}85 ; -4{.}14)}| and |\color{green}{B(10{.}63 ; 3{.}25)}.| |
|
|\begin{align} \dfrac{5\ \text{m}}{19{.}90\ \text{m}} &= \dfrac{1\ \text{sec}}{?\ \text{sec}} \\\\ \Rightarrow\ ? &= 1 \times 19{.}90 \div 5 \\ &\approx 3{.}98\ \text{sec} \end{align}| |
Determine the time the shark spends under the boat. |
|
The shark will have been under the boat for approximately |3{.}98| seconds. |
|
See also
To find the points of intersection between two conics, we generally rely on the following steps:
-
Determine the equation for each of the conics.
-
Solve the system of equations using one of the three methods (comparison, substitution, elimination).
-
Analyze the responses obtained to adequately choose the ones to keep.
-
Calculate the 2nd coordinate of each point of intersection using one of the two starting equations.
What are the coordinates of the intersection points of the following two conics:
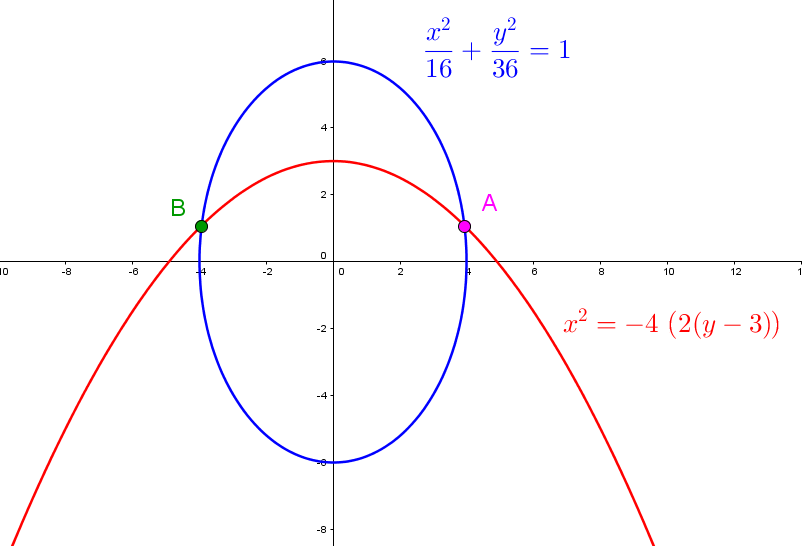
| CALCULATIONS | JUSTIFICATIONS |
|---|---|
|
|\color{blue}{\dfrac{x^2}{16}+\dfrac{y^2}{36}=1}| |\color{red}{x^2 = -4 \big(2 (y-3)\big)}| |
Find the equation of the two conics. |
|
|\dfrac{\color{red}{-4 \big(2 (y-3)\big)}}{\color{blue}{16}} \color{blue}{+ \dfrac{y^2}{36} = 1}| |
Substitute the value |\color{red}{x^2}| for |\color{blue}{x^2}.| |
|
|\begin{align} \dfrac{-8y+24}{16} + \dfrac{y^2}{36} &= 1 \\ \dfrac{36(-8y+24)+16(y^2)}{16\times 36} &=1\\ -288y + 864 + 16y^2 &= 576 \\ 16y^2 - 288y + 288 &= 0 \\ y^2-18y+18 &=0 \\\\ \Rightarrow\ \{y_1,y_2\} &= \dfrac{-(-18) \pm \sqrt{(-18)^2-4 (1)(18)}}{2 (1)} \\ \{y_1,y_2\} &\approx \dfrac{18 \pm \sqrt{252}}{2} \\ y_1 &\approx 16{.}94\quad \text{and}\quad y_2 \approx 1{.}06 \end{align}| |
Solve the new equation. |
|
|\begin{align} \color{red}{x^2} &\color{red}{=} \color{red}{-4 \big(2(} 1{.}06\color{red}{-3)\big)} \\ x^2 &= 15{.}52 \\ x &= \pm 3{.}94 \end{align}| |
According to the graph, we must reject the value |y_1| . We only use |y_2| to find the values in |x| sought. |
|
Thus, the coordinates of the intersection points are |\color{fuchsia}{A(3{.}94; 1{.}06)}| and |\color{green}{B(-3{.}94 ; 1{.}06)}.| |
|
See also
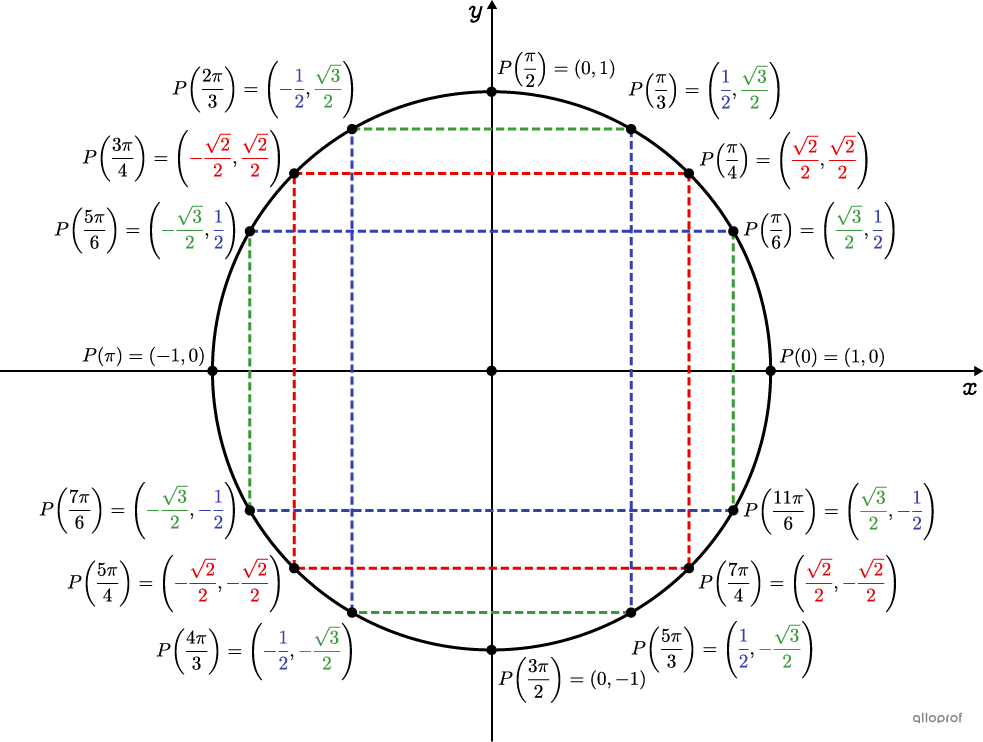From the drawing, note two factors:
-
The coordinates of points with the same colour are symmetrically related.
-
One full turn of the circle |=2\pi\ \text{rad}.|
What are the coordinates of the point associated with an angle of |\displaystyle \frac{-17\pi}{4}| ?
| CALCULATIONS | JUSTIFICATIONS |
|---|---|
|
|\displaystyle \frac{-17\pi}{4} + 2\pi = \frac{-17\pi}{4} + \frac{8\pi}{4} = \frac{-9\pi}{4}| |
Add or subtract a turn |(2\pi)| until the interval |[0, 2\pi]| is reached. |
|
|\displaystyle P\left(\frac{-17\pi}{4}\right) = P\left(\frac{7\pi}{4}\right) = \left(\frac{\sqrt{2}}{2}, \frac{-\sqrt{2}}{2}\right)| |
Associate the correct coordinates with the angle found. |