Voici un petit guide de préparation contenant toutes les notions abordées en quatrième secondaire dans la séquence TS. Pour expliquer le tout, chaque formule sera suivie d'un exemple et d'un lien qui mène à une fiche de notre bibliothèque virtuelle.
La division de polynômes se fait de la même façon que la division de deux nombres en utilisant la méthode par « crochet ».
Quel est le résultat de la division suivante :
| CALCULS | EXPLICATIONS |
|---|---|
| |
Déterminer le monôme par lequel il faut multiplier |2x + 8| pour annuler le terme en |x^2| du polynôme. |
|
Déterminer le monôme par lequel il faut multiplier |2x + 8| pour annuler le terme en |x| du polynôme. |
|
|
Identifier le reste lorsque le degré du résultat de la soustraction est plus petit que celui du binôme par lequel on divise. |
|
|
Le résultat de la division est |4x - 37| reste |26| ou |4x - 37 + \dfrac{26}{2x+8}.| |
|
À voir aussi
Pour additionner ou soustraire des expressions rationnelles, on peut généralement procéder en suivant les étapes ci-dessous :
-
Trouver un dénominateur commun.
-
Calculer les fractions équivalentes selon le dénominateur commun trouvé.
-
Effectuer l'addition ou la soustraction des termes semblables aux numérateurs.
-
Simplifer l'expression rationnelle finale en factorisant le numérateur et le dénominateur, si possible.
Simplifie l'expression algébrique suivante : ||\dfrac{x-2}{x+4} - \dfrac{3}{-3x-12}||
-
Trouver un dénominateur commun. ||\begin{align} &\dfrac{x-2}{x+4} - \dfrac{3}{-3x-12} \\ =\ &\dfrac{\color{red}{-3} (x-2)}{\color{red}{-3} (x+4)} - \dfrac{3}{-3x-12} \\ =\ &\dfrac{-3x+6}{-3x-12} - \dfrac{3}{-3x-12}\end{align}||
-
Effectuer l'opération sur les numérateurs. ||\begin{align} &\dfrac{-3x+6}{-3x-12} - \dfrac{3}{-3x-12} \\ =\ &\dfrac{(-3x+6) - (3)}{-3x-12} \\ =\ &\dfrac{-3x+3}{-3x-12} \end{align}||
-
Simplifier l'expression rationnelle en factorisant, si possible. Ici, on peut effectuer une simple mise en évidence au numérateur et au dénominateur. ||\begin{align} &\dfrac{-3x+3}{-3x-12} \\ =\ &\dfrac{-3(x-1)}{-3(x + 4)} \\ =\ &\dfrac{x-1}{x+4} \end{align}||
Réponse : Ainsi, le résultat de la différence de ces deux expressions rationnelles est |\dfrac{x-1}{x+4}.|
À voir aussi
Il est très important de maitriser le concept de distributivité associé à la multiplication :
-
Simplifier les expressions des parenthèses, si possible.
-
Distribuer chacun des termes de la première parenthèse sur tous les termes de la deuxième parenthèse.
-
Simplifier en additionnant et soustrayant les termes semblables.
Quelle est l'expression algébrique simplifiée de la multiplication suivante : ||(7x + 4) (2x^2 -4x +3)||
-
Distribuer chacun des termes de la première parenthèse avec les termes de la deuxième parenthèse. ||\begin{align} &(\color{blue}{7x} + \color{red}{4}) (2x^2 - 4x + 3) \\ =\ &\color{blue}{7x} \times 2x^2 + \color{blue}{7x} \times -4x + \color{blue}{7x} \times 3 + \color{red}{4} \times 2x^2 + \color{red}{4} \times -4x + \color{red}{4} \times 3 \\ =\ &14x^3 +-28x^2 + 21x + 8x^2 +-16x +12 \end{align}||
-
Effectuer les additions et les soustractions sur les termes semblables. ||\begin{align} &14x^3 +\color{blue}{-28x^2} + \color{green}{21x}+\color{blue}{8x^2} + \color{green}{-16x} + 12 \\ =\ &14x^3 + \color{blue}{-20x^2} + \color{green}{5x} + 12 \end{align}||
L'expression algébrique simplifiée est |14x^3 - 20x^2 + 5x +12.|
À voir aussi
Pour factoriser une même expression algébrique, on doit parfois utiliser plusieurs méthodes de factorisation. Ainsi, il est important de maitriser chacune d'entre elles tout en y associant leur forme polynomiale caractéristique.
| EXEMPLE DE LA MÉTHODE PRODUIT-SOMME | |
|---|---|
|
Quelles mesures (sous forme numérique ou d'expression algébrique) peuvent être associées à chacune des dimensions d'un prisme à base rectangulaire dont le volume est de |(4x^2 + 8x - 32 )\ \text{cm}^3|? |
|
| CALCULS | EXPLICATIONS |
|
|\begin{align} &4x^2 + 8x - 32 \\ =\ &4 (x^2 + 2x - 8) \end{align}| |
Si possible, faire une mise en évidence simple en s'assurant que tous les coefficients demeurent entier. |
|
|4 (\color{blue}{x}^2 + \color{red}{2x} \color{green}{-8})| Ainsi, les nombres sont |4| et |-2.| |
Déterminer les nombres qui répondent au produit et à la somme du polynôme entre parenthèses. |
|
|\begin{align} &4 (x^2 + \color{red}{2x} - 8) \\ =\ &4 (x^2 + \color{red}{4x -2x} - 8) \\ =\ &4(\left[x^2 + 4x\right] +\left[-2x -8\right]) \\ =\ &4 (\color{blue}{x} (\color{green}{x + 4}) \color{blue}{-2} (\color{green}{x + 4})) \\ =\ &4 (\color{green}{x+4}) (\color{blue}{x-2}) \end{align}| |
Séparer le terme en |\color{red}{x}| en utilisant les deux nombres trouvés. |
|
Ainsi, les trois dimensions mesurent respectivement |4,| |(x+4)| et |(x-2)\ \text{cm}.| |
|
| EXEMPLE DE DIFFÉRENCE DE CARRÉS | |
|---|---|
|
Quelles sont les expressions algébriques qui représentent la mesure de la base et de la hauteur d'un triangle dont l'aire est de |(2x^2 - 8)\ \text{m}^2|? |
|
| CALCULS | EXPLICATIONS |
|
|\begin{align} \dfrac{\color{blue}{b} \times \color{red}{h}}{2} &= 2x^2 - 8 \\ \color{blue}{b} \times \color{red}{h} &= 4x^2 - 16 \end{align}| |
Créer l'équation en lien avec la situation. |
|
|\sqrt{4x^2} = 2x| Il s'agit d'une soustraction entre les deux termes. |
Vérifier que le binôme répond aux critères d'une factorisation par différence de carrés. |
|
|\begin{align} \color{blue}{b} \times \color{red}{h} &= 4x^4 - 16 \\ \color{blue}{b} \times \color{red}{h} &= \color{blue}{(2x - 4)} \color{red}{ (2x + 4)} \end{align}| |
Factoriser selon ce modèle. |
|
Ainsi, on peut établir que |\color{blue}{b = (2x - 4)}| et |\color{red}{h = (2x + 4)}\ \text{m}.| |
|
| EXEMPLE DE TRINÔME CARRÉ PARFAIT | |
|---|---|
|
Quelle est l'expression algébrique associée à la mesure du côté d'un carré qui a une superficie de |(\color{blue}{9}x^2 - \color{red}{42}x +\color{green}{49})\ \text{m}^2?| |
|
| CALCULS | EXPLICATIONS |
|
|\begin{align} \sqrt{\color{blue}{a}} &= \sqrt{\color{blue}{9}} = \color{blue}{3} \\ \sqrt{\color{green}{c}} &= \sqrt{\color{green}{49}} = \color{green}{7} \\\\ \color{red}{b} &\overset{?}{=} 2 \sqrt{\color{blue}{a}} \sqrt{ \color{green}{c}} \\ \color{red}{42} &= 2 \times \color{blue}{3} \times \color{green}{7}=42\end{align}| |
Vérifier qu'il s'agit bien d'un trinôme carré parfait. |
|
|\color{blue}{9}x^2 - \color{red}{42}x + \color{green}{49}| |
Factoriser selon le modèle du trinôme carré parfait. |
|
Puisque l'aire d'un carré se calcule avec la formule |A = c^2,| on peut déduire que |A= (\color{blue}{3x} - \color{green}{7})^2.| Par associativité, on obtient que |c = (\color{blue}{3x} - \color{green}{7})\ \text{m}.| |
|
À voir aussi
Forme fonctionnelle
|y = ax + b| où | a = \dfrac{\Delta y}{\Delta x} = \dfrac{y_2 - y_1}{x_2 - x_1}|
Forme générale
|0 = Ax + By + C| où |A, B, C \in \mathbb{Z}|
Avec les informations qui sont fournies dans le graphique ci-dessous, détermine l'équation de la droite sous sa forme générale.
-
Trouver la pente selon |\dfrac{\Delta y}{\Delta x}.| ||a = \dfrac{2 - 4{,}4}{-0{,}5 - 0{,}5} = 2{,}4||
-
Trouver la valeur initiale |(b)| en substituant par un des points du graphique. ||\begin{align} f(x) &= 2{,}4 x + b\\ 2 &= 2{,}4 (-0{,}5) + b \\ b &= 3{,}2 \end{align}||
-
Transformer la valeur des paramètres |a| et |b| de la forme fonctionnelle sous la forme fractionnaire simplifiée. ||\begin{align} y &= 2{,}4x + 3{,}2 \\ y &= \dfrac{24}{10}x + \dfrac{32}{10} \\ y &= \dfrac{12}{5}x + \dfrac{16}{5} \end{align}||
-
Trouver un dénominateur commun pour tous les termes de l'équation. ||\begin{align} y &= \dfrac{12}{5}x + \dfrac{16}{5} \\ \Rightarrow\ \frac{5y}{5} &= \dfrac{12x}{5} + \dfrac{16}{5} \end{align}||
-
Rendre l'équation égale à |0.| ||\begin{align} \frac{5y}{\cancel{5}} &= \frac{12x}{\cancel{5}} + \frac{16}{\cancel{5}} \\ \Rightarrow 5y &= 12x + 16 \\ \Rightarrow\, \ 0 &= 12x - 5y + 16 \end{align}||
Réponse : L'équation de la droite sous sa forme générale est |0 = 12x - 5y + 16.|
À voir aussi
|y = a(bx)^2|
où |b = 1| à moins de travailler avec une mise en situation particulière.
Avec les informations qui sont fournies dans le tableau ci-dessous, détermine l'équation de la parabole.
| CALCULS | EXPLICATIONS |
|---|---|
|
|\begin{align} f(x) &= a x^2 \\ -6{,}75 &= a (-1{,}5)^2 \\ -3 &= a \end{align}| |
Substituer les valeurs de |x| et |y| par un point de la courbe pour trouver la valeur de |a.| |
|
L'équation de la parabole est |f(x) = -3 x^2.| |
|
Pour la fonction polynomial de degré 2 : |a \ne \dfrac{\Delta y}{\Delta x}|
À voir aussi
|f(x) = a \sqrt{bx}|
où |b=1| si la fonction est orientée vers la droite et |b=-1| si la fonction est orientée vers la gauche.
Quelle est l'équation de la fonction suivante :
| CALCULS | EXPLICATIONS |
|---|---|
|
|b = -1|, car la fonction est orientée vers la gauche. |
Déterminer la valeur du |b| selon l'orientation du graphique. |
|
|\begin{align}f(x) &= a \sqrt{-x} \\ 5 &= a \sqrt{-(-4)} \\ 5 &= a(2) \\ \dfrac{5}{2} &= a \end{align}| |
Remplacer |(x,y)| dans l'équation par les coordonnées d'un point du graphique. |
|
Ainsi, la règle associée à la courbe est |f(x) = \dfrac{5}{2} \sqrt{-x}.| |
|
À voir aussi
|y = a(c)^{bx}|
où
|a:| Valeur initiale
|c:| Base (facteur multiplicatif)
|b:| Fréquence du calcul
En 2005, la population des crapauds d'un étang s'élevait à 500. Pour différentes raisons, la population diminue de 5 % aux trois ans. Si le rythme se maintient, en quelle année y aura-t-il environ 368 crapauds?
| CALCULS | EXPLICATIONS |
|---|---|
|
|x:| Nombre d'années écoulées depuis 2005 |f(x):| Nombre de crapauds |
Définir les variables. |
|
|\begin{align} f(x) &= a (c)^{bx} \\ f(x) &= 500 (c)^{bx} \end{align}| |
Remplacer |a| par la valeur initiale, soit le nombre de crapauds en 2005. |
|
|\begin{align} f(x) &= 500 (c)^{bx} \\ f(x) &= 500 (0{,}95)^{\frac{x}{3}} \end{align}| |
Remplacer |c| par |0{,}95,| car |c = 1 - 5\ \text{%} = 1 - 0{,}05 = 0{,}95.| Remplacer |b| par |\dfrac{1}{3}| puisque la diminution de |5\ \text{%}| se fait tous les |3| ans. |
|
|\begin{align} f(18) &= 500 (0{,}95)^{\frac{18}{3}} \\ f(18) &\approx 368 \end{align}| |
En remplaçant |x| par différentes valeurs, on déduit que |x=18.| |
|
Avec |x=18,| cela implique que dans |18| ans, il y aura |368| crapauds. Puisque l'étude s'est déroulée en 2005, on en déduit que c'est en 2023 (2005 + 18) qu'il y aura environ |368| crapauds. |
|
À voir aussi
|f(x) = a \left[ b x\right]|
où
|{\mid}a{\mid} = | Distance verticale entre deux marches
|\dfrac{1}{{\mid}b{\mid}} = | Longueur d'une marche
Pour déterminer le signe de |a| et de |b,| on s'intéressera à l'ordre des points ouverts et fermés, la croissance et la décroissance du graphique :
Dans le cadre d'un nouveau programme de récompense, une épicerie offre des timbres qui permettent d'obtenir des réductions significatives à l'achat d'articles ciblés. Pour déterminer le nombre de timbres remis à chaque client, l'épicerie utilise le graphique suivant :
À l'aide de ce graphique, détermine les montants possibles de l'achat si un client a reçu 48 timbres.
-
Trouver la règle sous la forme |y = \color{red}{a} \left[\color{blue}{b}x\right]| ||\begin{align} {\mid}\color{red}{a}{\mid} &= 6 - 3 = \color{red}{3} \\ {\mid}\color{blue}{b}{\mid} &= \dfrac{1}{\text{Longueur d'une marche}} = \frac{1}{10} \end{align}||Selon l'orientation du graphique et de l'ordre des points ouverts et fermés, on en déduit que : ||y = \color{red}{-3} \left[ \color{blue}{-\frac{1}{10}}x\right]||
-
Trouver la valeur de |x| quand |y| vaut |48| ||\begin{align} y &= \color{red}{-3} \left[ \color{blue}{-\dfrac{1}{10}}x\right] \\ 48 &= \color{red}{-3} \left[ \color{blue}{-\dfrac{1}{10}}x\right] \\ -16 &= \left[ \color{blue}{-\dfrac{1}{10}}x\right] \\ -16 &< \color{blue}{-\dfrac{1}{10}}x\quad \text{ou}\quad -15 \geq \color{blue}{-\dfrac{1}{10}}x \\ 160 &> x\qquad\quad\, \text{ou}\quad\ \ \ 150 \leq x \end{align}||
-
Déterminer l'intervalle en |x| de la solution ||x \in \left[150, 160\right[||
Réponse : Le montant d'achat est d'au moins |150\ $,| mais de moins de |160\ $.|
À voir aussi
Dans une fonction périodique, un cycle fait référence au motif qui se répète alors que la période est la durée du cycle selon l'axe des |x.|
De retour de vacance, Marie-Claude décide de se remettre en forme en faisant du vélo avec son groupe d'amies. Pour guider le groupe, un entraineur fait le trajet avec eux et c'est lui qui décide de la vitesse à maintenir. Afin de préparer le groupe à la prochaine séance, l'entraineur remet ce graphique à chacun des membres du groupe :
En sachant que l'entrainement consiste à répéter le même trajet pendant 45 minutes, Marie-Claude se demande pendant combien de minutes, au total, elle aura pédalé à une vitesse minimale de 16 km/h?
| CALCULS | EXPLICATIONS |
|---|---|
| |
Identifier les endroits où la vitesse est de 16 km/h sur le premier cycle. |
| |
Identifier des points sur chacune des droites sur lesquelles se situe la vitesse minimale recherchée. |
|
|a = \dfrac{\Delta y}{\Delta x} = \dfrac{24-12}{4-3} = 12| Ainsi, |y = 12x + b| Par substitution de x et y, Finalement, |\color{green}{y=12x - 24}| |
Trouver l'équation de |\color{green}{\text{la droite verte}}.| Par ailleurs, on utilise les points |(3,12)| et |(4,24)| puisqu'ils sont sur |\color{green}{\text{la droite verte}}.| |
|
|\begin{align} 16 &= 12x - 24 \\ 40 &= 12x \\ \color{green}{3{,}33} &\approx x \end{align}| |
Remplacer le |y| par |16| pour trouver le temps en minute du |\color{green}{\text{point vert}}.| |
|
|a = \dfrac{\Delta y}{\Delta x} = \dfrac{24-0}{4-6} = -12| Ainsi, |y = -12x + b| Par substitution de x et y, Finalement, |\color{blue}{y=-12x + 72}| |
Trouver l'équation de |\color{blue}{\text{la droite bleue}}.| Par ailleurs, on utilise les points |(4,24)| et |(6,0)| puisqu'ils sont sur |\color{blue}{\text{la droite bleue}}.| |
|
|\begin{align} 16 &= -12x + 72 \\ -56 &= -12x \\ \color{blue}{4{,}67} &\approx x\end{align}| |
Remplacer le |y| par |16| pour trouver le temps en minute du |\color{blue}{\text{point bleu}}.| |
|
|\color{blue}{4{,}67} - \color{green}{3{,}33} = \color{red}{1{,}34 \ \text{min}}| |
Déterminer la durée entre |\color{green}{\text{le point vert}}| et |\color{blue}{\text{le point bleu}}.| |
|
|6 - 0 = 6 \ \text{min}| |
Déterminer la période du cycle qui est répété. |
|
|\begin{align} \text{Nbre de cycles} &= \dfrac{\text{Durée totale du trajet}} {\text{Durée d'un cycle}} \\ \text{Nbre de cycles} &= \dfrac{45}{6} \\ \text{Nbre de cycles} &=7{,}5 \end{align}| |
Déterminer le nombre de cycles complets dans le trajet. |
|
|7{,}5| équivaut à |7| cycles complets |(7 \times 6 = 42\ \text{min})| et la moitié d'un cycle. Ainsi, l'intervalle de |1{,}34| minute se répète à sept reprises exactement. |
Analyser le cycle incomplet pour déterminer si la portion répond à la question initiale (vitesse minimale de 16 km/h). |
|
|\begin{align} \text{Durée totale} &= \color{red}{\text{Durée d'un cycle}} \times \text{Nbre de périodes} \\ \text{Durée totale} &= \color{red}{1{,}34} \times 7 \\ \text{Durée totale} &= 9{,}38 \end{align}| |
Déterminer la durée totale de l'intervalle analysé. |
|
À la fin de son entrainement, Marie-Claude aura passé un total de |9{,}38| minutes à pédaler à une vitesse d'au moins 16 km/h. |
|
À voir aussi
La réciproque d'une fonction |f(x)|, notée |f^{-1}(x)|, s'obtient en inversant les coordonnées des points tel que |(x,y) \rightarrow (y,x)|
Trace la réciproque de la fonction suivante :
| CALCULS | EXPLICATIONS |
|---|---|
| |
Créer une table des valeurs selon les points donnés. |
| |
Inverser les coordonnées |(\color{blue}{x}, \color{red}{y}) \rightarrow (\color{red}{y}, \color{blue}{x}).| |
|
Tracer le graphique de la réciproque à l'aide de cette nouvelle table des valeurs. |
La réciproque d'une fonction ne donne pas toujours une fonction. Dans les cas étudiés ici, voici les fonctions qui sont réciproques les unes des autres :
-
Les fonctions exponentielles et logarithmiques
-
La fonction affine par rapport à elle-même
-
La fonction de degré deux (avec un domaine restreint) et la fonction racine carrée
À voir aussi
Pour l'étude d'une fonction, ce sont toujours les mêmes propriétés qu'il faut analyser :
-
le domaine : toutes les valeurs possibles de |x|
-
le codomaine (l'image) : toutes les avleurs possibles de |y|
-
les abscisses à l'origine : la valeur du |x| quand |y=0|
-
l'ordonnée à l'origine : la valeur du |y| quand |x=0|
-
maximum : la plus grande valeur de |y|
-
minimum : la plus petite valeur de |y|
-
croissance : quand le graphique ne « descend » pas
-
décroissance : quand le graphique ne « monte » pas
-
Le signe :
-
positive : portion du graphique qui est au-dessus ou égale à l'axe des |x|
-
négative : portion du graphique qui est en-dessous ou égale à l'axe des |x|
-
En tant que comptable d'une grande compagnie, tu dois donner un compte rendu détaillé de l'évolution des profits au cours de la dernière année. Pour t'aider, voici le graphique des 12 derniers mois.
Avant de préparer ton discours de présentation et afin de bien alimenter ton argumentation, tu dois faire l'étude complète du graphique.
| PROPRIÉTÉS | EXPLICATIONS |
|---|---|
|
Domaine : |[0, 12]| |
La valeur la plus petite sur l'axe des |x| est |0| et la plus grande est |12.| |
|
Image : |[-5, 20]| |
La valeur la plus petite sur l'axe des |y| est |-5| et la plus grande est |20.| |
|
Croissance : |[0, 4] \cup [9, 12]| |
En analysant les valeurs de |x|, ce sont les deux portions du graphique qui montent ou qui sont constantes. |
|
Décroissance : |[4, 10]| |
En analysant les valeurs de |x|, c'est la seule portion du graphique qui descend ou qui est constante. |
|
Maximum : |\left\{ 20 \right\}| |
Selon les valeurs de |y|, c'est la plus grande valeur atteinte par le graphique. |
|
Minimum : |\left\{ -5 \right\}| |
Selon les valeurs de |y|, c'est la plus petite valeur atteinte par le graphique. |
|
Zéros de fonctions : |(0,0) , (8,0) , (11,0)| |
Ce sont les coordonnées des points où le graphique touche à l'axe des |x.| |
|
Ordonnée à l'origine : |(0,0)| |
C'est la coordonnée du point où le graphique touche à l'axe des |y.| |
|
Positive : | [0,8] \cup [11,12]| |
Selon les valeurs de |x|, ce sont les portions du graphique qui sont au-dessus ou égales à l'axe des |x.| |
| Négative : |\{0\} \cup [8,11]| | Selon les valeurs de |x,| ce sont les portions du graphique qui sont en-dessous ou égales à l'axe des |x.| |
À voir aussi
Pour résoudre un système d'équations par comparaison, on peut se fier aux étapes suivantes :
-
Identifier les variables reliées aux inconnus.
-
Créer les équations selon la mise en situation.
-
Isoler la même variable pour chacune des équations.
-
Comparer les deux équations pour en former une nouvelle.
-
Résoudre cette nouvelle équation.
-
Remplacer la valeur de la variable dans une des équations de départ pour trouver la valeur de l'autre variable.
Au dépanneur du coin, un groupe de travailleurs achètent 4 cafés et 6 muffins pour |15{,}06\ $.| Le lendemain, ce même groupe se procure 3 cafés et 5 muffins pour une somme de |11{,}97\ $.| Si, le jour d'après, ces travailleurs veulent se procurer 6 cafés et 4 muffins, quelle somme devra être déboursée?
-
Identifier les inconnus à l'aide de variables
|x=| cout pour un café |($)|
|y=| cout pour un muffin |($)| -
Créer un système d'équations ||\color{blue}{4x + 6y = 15{,}06}\\ \color{red}{3x + 5y = 11{,}97}||
-
Transformer chacune des équations sous la forme fonctionnelle ||\begin{align} y &= \color{blue}{2{,}51 - \dfrac{4}{6}x} \\ y &= \color{red}{2{,}394 - \dfrac{3}{5}x} \end{align}||
-
Comparer les deux équations ||\color{blue}{2,51 - \dfrac{4}{6}x} = \color{red}{2,394 -\dfrac{3}{5}x}||
-
Trouver la valeur de |x| en l'isolant avec les opérations inverses ||\begin{align} \color{blue}{2{,}51 - \dfrac{4}{6}x} &= \color{red}{2{,}394 - \dfrac{3}{5}x} \\ 2{,}51 - 2{,}394 &= -\dfrac{3}{5}x + \dfrac{4}{6}x \\ 0{,}116 &= \dfrac{1}{15}x \\ 1{,}74 &= x \end{align}||
-
Substituer la valeur de |x| dans une des deux équations de départ pour trouver la valeur de |y| ||\begin{align} 4x + 6y &= 15{,}06 \\ 4 (1{,}74) + 6y &= 15{,}06 \\ y &= 1{,}35 \end{align}||
-
Calculer le montant recherché selon |6| cafés et |4| muffins ||\begin{align} 6 \ \text{cafés} + 4\ \text{muffins} &=\ ? \\ 6x + 4y &=\ ? \\ 6 (1{,}74) + 4 (1{,}35) &=\ ? \\ 15{,}84 &=\ ? \end{align}||
Réponse : Il en coutera |15{,}84\ $.|
À voir aussi
Pour résoudre une système d'équations par substitution, on peut se fier aux étapes suivantes :
-
Identifier les variables reliées aux inconnus.
-
Créer les équations selon la mise en situation.
-
Isoler une variable dans une des deux équations.
-
Substituer cette même variable dans l'autre équation par l'expression algébrique qui lui est associée.
-
Résoudre cette nouvelle équation.
-
Remplacer la valeur de la variable dans une des équations de départ pour trouver la valeur de l'autre variable.
Au dépanneur du coin, un groupe de travailleurs achètent 4 cafés et 6 muffins pour |15{,}06\ $.| Le lendemain, ce même groupe se procure 3 cafés et 5 muffins pour une somme de |11{,}97\ $.| Si, le jour d'après, ces travailleurs veulent se procurer 6 cafés et 4 muffins, quelle somme devra être déboursée?
-
Identifier les inconnus à l'aide de variables
|x=| cout pour un café |($)|
|y=| cout pour un muffin |($)| -
Créer un système d'équations ||\color{blue}{4x + 6y = 15{,}06}\\ \color{red}{3x + 5y = 11{,}97}||
-
Transformer une des deux équations sous la forme fonctionnelle ||\begin{align} \color{blue}{4x + 6y} &= \color{blue}{15{,}06} \\ \color{blue}{y} &= \color{blue}{2{,}51 - \dfrac{4}{6}x} \end{align}||
-
Substituer le |y| dans l'autre équation ||\begin{align} \color{red}{3x + 5}\color{blue}{y} &= \color{red}{11{,}97} \\ \color{red}{3x + 5} \color{blue}{\left(2{,}51 - \dfrac{4}{6}x \right)} &= \color{red}{11{,}97} \end{align}||
-
Trouver la valeur de |x| en l'isolant avec les opérations inverses ||\begin{align} \color{red}{3x + 5} \color{blue}{\left(2{,}51 - \frac{4}{6}x\right)} &= \color{red}{11{,}97} \\ 3x + 12{,}55 - \frac{20}{6}x &= 11{,}97 \\ x &= 1{,}74 \end{align}||
-
Substituer la valeur de |x| dans une des deux équations de départ pour trouver la valeur de |y| ||\begin{align} 4x + 6y &= 15{,}06 \\ 4 (1{,}74) + 6y &= 15{,}06 \\ y &= 1{,}35 \end{align}||
-
Calculer le montant recherché selon |6| cafés et |4| muffins ||\begin{align} 6 \ \text{cafés} + 4\ \text{muffins} &=\ ? \\ 6x + 4y &=\ ? \\ 6 (1{,}74) + 4 (1{,}35) &=\ ? \\ 15{,}84 &=\ ? \end{align}||
Réponse : Il en coutera |15{,}84\ $.|
À voir aussi
Pour résoutre un système d'équation par réduction, on peut se fier aux étapes suivantes :
-
Identifier les variables reliées aux inconnus.
-
Créer les équations selon la mise en situation.
-
Trouver des équations équivalentes pour obtenir le même coefficient d'une même variable.
-
Soustraire les deux équations.
-
Isoler la variable restante pour trouver sa valeur.
-
Remplacer la valeur de la variable dans une des équations de départ pour trouver la valeur de l'autre variable.
Au dépanneur du coin, un groupe de travailleurs achètent 4 cafés et 6 muffins pour |15{,}06\ $.| Le lendemain, ce même groupe se procure 3 cafés et 5 muffins pour une somme de |11{,}97\ $.| Si, le jour d'après, ces travailleurs veulent se procurer 6 cafés et 4 muffins, quelle somme devra être déboursée?
-
Identifier les inconnus à l'aide de variables
|x=| cout pour un café |($)|
|y=| cout pour un muffin |($)| -
Créer un système d'équations ||\color{blue}{4x + 6y = 15{,}06}\\ \color{red}{3x + 5y = 11{,}97}||
-
Trouver des équations équivalentes afin d'obtenir le même coefficient en |x| dans chacune des équations ||\begin{align} 3\big( \color{blue}{4x + 6y} = \color{blue}{15{,}06}\big) &\Rightarrow \color{blue}{12x + 18y = 45{,}18} \\ 4 \big(\color{red}{3x + 5y} = \color{red}{11{,}97}\big) &\Rightarrow \color{red}{12x + 20y = 47{,}88} \end{align}||
-
Effectuer la réduction (soustraction) de chacun des termes semblables ||\begin{align} \color{blue}{12x + 18y} &= \color{blue}{45{,}18} \\ -\big(\color{red}{12x + 20y} &= \color{blue}{47{,}88}\big)\\ \hline -2y &=-2{,}70 \end{align}||
-
Trouver la valeur de |y| en l'isolant avec les opérations inverses ||\begin{align} -2y &=-2{,}70 \\ y &= 1{,}35 \end{align}||
-
Substituer la valeur de |y| dans une des deux équations de départ pour trouver la valeur de |x| ||\begin{align} 4x+6y &= 15{,}06 \\ 4x+6(1{,}35) &=15{,}06 \\ x &= 1{,}74 \end{align}||
-
Calculer le montant recherché selon |6| cafés et |4| muffins ||\begin{align} 6 \ \text{cafés} + 4\ \text{muffins} &=\ ? \\ 6x + 4y &=\ ? \\ 6 (1{,}74) + 4 (1{,}35) &=\ ? \\ 15{,}84 &=\ ? \end{align}||
Réponse : Il en coutera |15{,}84\ $.|
À voir aussi
De façon générale, c'est la loi sur la multiplication des radicaux qui est utilisé pour effectuer la factorisation |(\sqrt { ab} = \sqrt{a} \sqrt{b}).| Pour y arriver :
-
Décomposer le radicande en un produit de facteurs dont un est un nombre carré.
-
Transformer la racine d'un produit en un produit de racine |(\sqrt{ab} = \sqrt{a}\sqrt{b}).|
-
Calculer la racine du nombre carré.
Quelle est la valeur simplifiée de la racine suivante : ||\sqrt{45}||
| CALCULS | EXPLICATIONS |
|---|---|
|
|\sqrt{45} = \sqrt{\color{blue}{9} \times 5}| |
Factoriser le radicande en un produit de facteurs dont un est un nombre carré. |
|
|\begin{align} &\sqrt{\color{blue}{9} \times 5} \\=\ &\sqrt{\color{blue}{9}} \sqrt {5} \end{align}| |
Utiliser la loi du produit des radicaux : |\sqrt{a b} = \sqrt{a} \sqrt{b}.| |
|
|\begin{align} \sqrt{\color{blue}{9}} \sqrt {5} \\ =\ \color{blue}{3} \sqrt {5} \end{align}| |
Calculer la racine carrée. |
|
Ainsi, |\sqrt{45} = 3 \sqrt{5}.| |
|
À voir aussi
Selon le triangle rectangle qui suit, on peut en déduire 3 théorèmes.
-
Dans un triangle rectangle, la mesure de chaque côté de l’angle droit est moyenne proportionnelle entre la mesure de sa projection sur l’hypoténuse et celle de l’hypoténuse entière.||\begin{align} \dfrac{m}{a} = \dfrac{a}{c}\ &\Leftrightarrow\ a^2 = m c \\\\ \dfrac{n}{b} = \dfrac{b}{c}\ &\Leftrightarrow\ b^2 = n c \end{align}||
-
Dans un triangle rectangle, la mesure de la hauteur issue du sommet de l’angle droit est moyenne proportionnelle entre les mesures des deux segments qu’elle détermine sur l’hypoténuse. ||\dfrac{m}{h} = \dfrac{h}{n}\ \Leftrightarrow\ h^2 = m n||
-
Dans le triangle rectangle, le produit des mesures de l’hypoténuse et de la hauteur correspondante égale le produit des mesures des côtés de l’angle droit. ||c h = a b||
Afin de se distinguer des autres entrepreneurs, une compagnie de construction suggère des maisons avec des toits de différentes formes. Parmi ces choix, on a la forme suivante :
Afin d'estimer les couts de production, l'entrepreneur a besoin des deux mesures extérieures manquantes de ce triangle |(\overline {AB}, \overline {BC}).| Aide-le à les déterminer.
| CALCULS | EXPLICATIONS |
|---|---|
|
|\begin{align} &a\; = 6{,}5 \\ &m = 4{,}1 \\ &c \ (m\overline {AB}) =\ ? \\ &b \ (m\overline {BC}) =\ ? \end{align}| |
Associer toutes les mesures connues et recherchées à une des mesures du dessin de référence. |
|
|\begin{align} a^2 &= m c \\ 6{,}5^2 &= 4{,}1 c \end{align}| |
Choisir le théorème pour laquelle on aura une seule inconnue : Dans un triangle rectangle, la mesure de chaque côté de l’angle droit est moyenne proportionnelle entre la mesure de sa projection sur l’hypoténuse et celle de l’hypoténuse entière. |
|
|\begin{align} 6{,}5^2 &= 4{,}1 c \\ 42{,}25 &= 4{,}1 c \\ \dfrac{42{,}25}{\color{red}{4{,}1}} &= \dfrac{4{,}1c}{\color{red}{4{,}1}} \\ 10{,}3 &\approx c \end{align}| |
Résoudre l'équation. |
|
|\begin{align} a^2 + b^2 &= c^2 \\ 6{,}5^2 + m\overline {BC}^2 &= 10{,}3^2 \\ 42{,}25 + m\overline {BC}^2 &\approx 106{,}09 \\ m\overline {BC}^2 &\approx 63{,}84 \\ m\overline {BC} &\approx 8 \end{align}| |
Appliquer la relation de Pythagore dans le grand triangle rectangle vert pour trouver la mesure de la cathète manquante. |
|
Ainsi, |m \overline {AB} \approx 10{,}3 \ \text{m}| et |m \overline {BC} \approx 8 \ \text{m}.| |
|
À voir aussi
En considérant l'angle |\theta| comme référence, on a :
|\sin \theta = \dfrac{\text{Mesure du côté opposé à }\ \theta}{\text{Mesure de l'hypoténuse}}|
|\cos \theta = \dfrac{\text{Mesure du côté adjacent à }\ \theta}{\text{Mesure de l'hypoténuse}}|
|\tan \theta = \dfrac{\text{Mesure du côté opposé à} \ \theta}{\text{Mesure du côté adjacent à} \ \theta}|
Afin de s'assurer de respecter les normes du bâtiment, l'angle d'élévation des fermes de toit d'une maison doit être d'un minimum de |25^\circ.| Pour s'assurer de respecter cette contrainte, un fabriquant décide d'établir cet angle à |35^\circ.| Si on sait que la longueur de la ferme de toit est de 13 mètres, quelles seront les mesures des deux autres côtés de cette pièce de bois?
| CALCULS | EXPLICATIONS |
|---|---|
|
|\sin \color{red}{35^\circ} = \dfrac{\color{red}{c}}{\color{green}{13}}| |
Identifier le bon rapport trigonométrique : |\sin \theta = \dfrac{\text{Opposé}}{\text{Hypoténuse}}| |
|
|\begin{align} \sin \color{red}{35^\circ} &= \dfrac{\color{red}{c}}{\color{green}{13}} \\ \color{green}{13}\sin \color{red}{35^\circ} &= \color{red}{c} \\ 7{,}46 &\approx \color{red}{c} \end{align}| |
Résoudre l'équation. |
|
|\cos \color{red}{35^\circ} = \dfrac{\color{blue}{b}}{\color{green}{13}}| |
Identifier le bon rapport trigonométrique : |\cos \theta = \dfrac{\text{Adjacent}}{\text{Hypoténuse}}| |
|
|\begin{align} \cos \color{red}{35^\circ} &= \dfrac{\color{blue}{b}}{\color{green}{13}} \\ \color{green}{13} \cos \color{red}{35^\circ} &= \color{blue}{b} \\ 10{,}65 &\approx \color{blue}{b} \end{align}| |
Résoudre l'équation. |
|
Ainsi, |\color{blue}{m \overline {AC}} \approx 10{,}65 \ \text{m}| et |\color{red}{m \overline {AB}} \approx 7{,}46 \ \text{m}.| |
|
Afin de déterminer le trajet à suivre par un hélicoptère pour aller chercher des gens en détresse en forêt, on a triangulé la carte de la région avec l'emplacement actuel de l'hélicoptère, l'hôpital et les gens qui sont en détresse.
Selon ce dessin, quelle orientation devrait suivre l'hélicoptère pour se rendre le plus rapidement possible aux gens en détresse?
| CALCULS | EXPLICATIONS |
|---|---|
|
|\tan ? = \dfrac{\color{red}{18{,}5}}{\color{blue}{12}}| |
Identifier le bon rapport trigonométrique : |\tan \theta = \dfrac{\text{Opposé}}{\text{Adjacent}}| |
|
|\begin{align} \tan ? &= \dfrac{\color{red}{18{,}5}}{\color{blue}{12}} \\ \tan ? &\approx 1{,}54 \\ ? &= \tan^{-1}(1{,}54) \\ ? &\approx 57^\circ \end{align}| |
Résoudre l'équation. |
|
L'angle d'orientation de l'hélicoptère devrait être de |57^\circ.| |
|
À voir aussi
Pour y arriver, il faut ajouter des lignes (généralement une hauteur) avec des propriétés particulières et des mesures indéterminées.
-
Choisir le bon sommet à partir duquel on trace une hauteur.
-
Utiliser les rapports trigonométriques dans le triangle rectangle pour trouver les mesures manquantes.
-
Appliquer la formule d'aire d'un triangle avec les mesures trouvées.
Quelle est l'aire du triangle suivant :
| CALCULS | EXPLICATIONS |
|---|---|
| |
Trouver toutes les mesures d'angle, si possible (Somme des angles intérieurs d'un triangle |= 180^\circ|). |
| |
Tracer une hauteur pour faire en sorte qu'elle soit l'inconnue dans le rapport trigonométrique utilisée. |
| |
Identifier le triangle rectangle ainsi formé. |
|
|\begin{align} \sin \color{red}{24^\circ} &= \dfrac{\color{blue}{h}}{42} \\ 17{,}08 &\approx \color{blue}{h} \\\\ \cos \color{red}{24^\circ} &= \dfrac{\color{green}{b}}{42} \\ 38{,}37 &\approx \color{green}{b} \end{align}| |
Trouver le plus de mesures possible à l'aide des rapports trigonométriques. |
| |
Trouver les mesures d'angle manquantes du petit triangle de gauche. |
|
|\begin{align} \tan \color{red}{48^\circ} &= \dfrac{\color{blue}{17{,}08}}{\color{green}{2^\text{e}\text{ cathète}}} \\ 15{,}38 &\approx \color{green}{2^\text{e}\text{ cathète}} \end{align}| |
Trouver la mesure de la 2e cathète du petit rectangle. |
| |
Déduire la mesure de la base du triangle initiale. |
| |
Identifier la base et la hauteur à utiliser pour calculer l'aire du triangle. |
|
|\begin{align} A &= \dfrac{b \times \color{blue}{h}}{2} \\ A &= \dfrac{22{,}99 \times \color{blue}{17{,}08}}{2} \\ &\approx 196{,}33 \ \text{cm}^2 \end{align}| |
Calculer l'aire du triangle selon sa formule. |
|
L'aire du triangle est d'environ |196{,}33 \ \text{cm}^2.| |
|
À voir aussi
-
A - C - A : Deux triangles sont isométriques quand une paire de côtés homologues isométriques est incluse entre deux paires d'angles homologues isométriques.
-
C - A - C : Deux triangles sont isométriques quand une paire d'angles homologues isométriques est incluse entre deux paires de côtés homologues isométriques.
-
C - C - C : Deux triangles sont isométriques quand chacune des paires de côtés homologues sont isométriques.
Dû à des problèmes de machinerie, les employés d'une compagnie de construction doivent monter eux-mêmes les fermes de toit de forme triangulaire afin de terminer la construction d'une maison. Or, ils doivent s'assurer qu'elles soient toutes identiques.
Avec les informations fournies ci-dessus, démontre que ces deux constructions sont isométriques.
| AFFIRMATIONS | JUSTIFICATIONS |
|---|---|
|
|\angle \color{red}{BAC} \cong \angle \color{green}{EFG}| |
|m \angle \color{green}{EFG} = 180^\circ - 130^\circ - 17^\circ = 33^\circ = m \angle \color{red}{BAC}| |
|
|\color{red}{\overline{AB}} \cong \color{green}{\overline{EF}}| |
Par hypothèse |
|
|\angle \color{red}{ABC} \cong \angle \color{green}{DEF}| |
Par hypothèse |
|
Le |\Delta \color{red}{ABC} \cong \Delta \color{green}{DEF}| par la condition minimale de A-C-A. |
|
À voir aussi
-
A - A : Deux triangles sont semblables quand deux paires d'angles homologues sont isométriques.
-
C - A - C : Deux triangles sont semblables quand une paire d'angles homologues isométriques est incluse entre deux paires de côtés homologues proportionnels.
-
C - C - C : Deux triangles sont semblables si les trois paires de côtés homologues sont proportionnels.
Dans le cadre d'une levée de fonds pour un organisme communautaire, la ville organise une course à pied à faire en famille. Par ailleurs, ils tiennent à ce que le trajet fait par les adultes soit semblable à celui des enfants.
En tenant compte des informations données ci-dessus, démontre que les deux trajets sont semblables.
| AFFIRMATIONS | JUSTIFICATIONS |
|---|---|
|
|\dfrac{m\color{green}{\overline{AC}}}{m \color{blue}{\overline {DF}}} = \dfrac{m\color{green}{\overline{AB}}}{m \color{blue}{\overline {DE}}}= \dfrac{m\color{green}{\overline{BC}}}{m \color{blue}{\overline {EF}}}| |
|\begin{align} \dfrac{\color{green}{1{,}4}}{\color{blue}{3{,}5}} &= \dfrac{\color{green}{1{,}1}}{\color{blue}{2{,}75}}= \dfrac{\color{green}{0{,}8}}{\color{blue}{2}} \\ \dfrac{2}{5}\ \ &=\ \ \dfrac{2}{5}\ \ \ =\ \ \dfrac{2}{5}\end{align}| |
|
Ainsi, |\Delta \color{green}{ABC} \sim \Delta \color{blue}{DEF}| par la condition minimale C-C-C. |
|
À voir aussi
|\text{Distance} = \sqrt{(y_2 - y_1)^2 + (x_2 - x_1)^2}|
où
|(x_1, y_1):| Coordonnées du point situé au début du segment
|(x_2, y_2):| Coordonnées du point situé à l'autre extrémité du segment
Afin de déterminer la quantité d'essence qu'un avion doit avoir dans son réservoir pour faire un vol Montréal-Paris, on représente chacune de ces deux villes sur un plan cartésien gradué en kilomètre.
Quelle est la distance, en kilomètres, entre ces deux villes?
| CALCULS | EXPLICATIONS |
|---|---|
|
Montréal |= (\color{blue}{x_1}, \color{red}{y_1}) = (\color{blue}{512}, \color{red}{647})| |
Identifier les points |(x_1, y_1)| et |(x_2, y_2).| |
|
|\begin{align} \text{Distance} &= \sqrt{(y_2 - \color{red}{y_1})^2 + (\color{green}{x_2} - \color{blue}{x_1})^2} \\ \text{Distance} &= \sqrt{(1\ 603 - \color{red}{647})^2 + (\color{green}{5\ 936} - \color{blue}{512})^2} \end{align}| |
Substituer les valeurs dans la formule. |
|
|\begin{align} \text{Distance} &= \sqrt{(1\ 603 - \color{red}{647})^2 + (\color{green}{5\ 936} - \color{blue}{512})^2} \\ \text{Distance} &= \sqrt{ 956^2 + 5\ 424^2} \\ \text{Distance} &\approx 5\ 507{,}6 \ \text{km} \end{align}| |
Résoudre l'équation. |
|
La distance entre Montréal et Paris est d'environ |5\ 507{,}6 \ \text{km}.| |
|
À voir aussi
Soit |(x,y),| les coordonnées du point de partage recherchée. ||x=x_1+ \dfrac{a}{b} (x_2-x_1)|| ||y=y_1+ \dfrac{a}{b} (y_2-y_1)||
où
|(x_1,y_1):| Coordonnées du début du segment
|(x_2,y_2):| Coordonnées de fin du segment
|\dfrac{a}{b}:| Fraction qui définit le partage du segment
À chaque matin, tu dois te rendre à l'arrêt d'autobus pour attendre ton moyen de transport qui te reconduit à ton école. Afin que l'arrêt soit centralisé pour les autres élèves du coin, tu as remarqué qu'il partageait le segment de rue qui rejoint ta maison à ton école dans un rapport |1 : 4.|
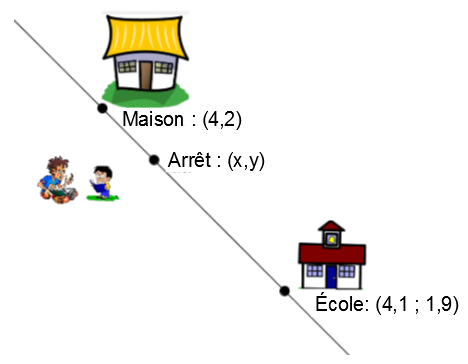
En utilisant les informations disponibles, détermine la coordonnée de l'endroit où se situe ton arrêt d'autobus.
-
Identifier le point de départ et le point d'arrivée. ||\begin{align} \text{Maison} &=(\color{blue}{x_1},\color{red}{y_1})= (\color{blue}{4},\color{red}{2}) \\ \text{École} &=(\color{green}{x_2},y_2)= (\color{green}{4{,}1};1{,}9) \end{align}||
-
Trouver la fraction |\dfrac{a}{b}| associée au rapport. ||1:4=\dfrac{1}{1+4}=\dfrac{1}{5}||
-
Substituer les valeurs dans la formule et résoudre l'équation pour trouver la coordonnée en |x| du point de partage. ||\begin{align} x &= \color{blue}{x_1}+\dfrac{a}{b}(\color{green}{x_2}-\color{blue}{x_1}) \\ x&= \color{blue}{4}+\dfrac{1}{5}(\color{green}{4{,}1}-\color{blue}{4}) \\ x &= 4{,}02 \end{align}||
-
Substituer les valeurs dans la formule et résoudre l'équation pour trouver la coordonnée en |y| du point de partage. ||\begin{align} y &= \color{red}{y_1}+\dfrac{a}{b}(y_2-\color{red}{y_1}) \\ y&= \color{red}{2}+\dfrac{1}{5}(1{,}9-\color{red}{2}) \\ y &= 1{,}98 \end{align}||
Réponse : Les coordonnées du point de partage |(x,y)| est |(4{,}02;1{,}98).|
Il est important de bien différencier les deux types de notations utilisées pour illustrer la portion associée à un point de partage pour ensuite utiliser la notation appropriée à la formule : ||\begin{matrix}\text{Rapport} \\ \Large{a:b} \end{matrix} \Leftrightarrow\ \begin{matrix}\text{Fraction} \\ \large\frac{a}{a+b} \end{matrix}||
À voir aussi
Les droites |y_1 = a_1 x + b_1| et |y_2 = a_2 x + b_2| sont parallèles si et seulement si |a_1 = a_2.|
Quelle est l'équation de la droite qui est parallèle à celle identifiée dans le plan cartésien ci-dessous et qui passe par le point C?
| CALCULS | EXPLICATIONS |
|---|---|
|
|a = \dfrac{\Delta y}{\Delta x} = \dfrac{0{,}7 - 2{,}5}{1{,}5 - 0} = -1{,}2| |
Trouver la pente de |\overline{AB}.| |
|
|\begin{align} y &= -1{,}2x + b \\ 2{,}25 &= -1{,}2 (1{,}55) + b \\ 2{,}25 &= -1{,}86 + b \\ 4{,}11 &= b \end{align}| |
Trouver l'équation de la droite passant par |C (1{,}55 ; 2{,}25)| sous la forme |y = ax + b.| Dans ce cas, la valeur de |a| de l'équation recherchée est la même que celle de |\overline{AB}| puisque les droites sont parallèles. |
|
Finalement, l'équation de la droite qui est parallèle à |\overline{AB}| et qui passe par le point | C (1{,}55 ; 2{,}25)| est |y = -1{,}2x + 4{,}11.| |
|
Les droites |y_1 = a_1 x + b_1| et |y_2 = a_2 x + b_2| sont perpendiculaires si et seulement si |a_1 \times a_2 = -1.|
On dit aussi que deux droites sont perpendiculaires si la pente de l'une est l'opposée de l'inverse de la pente de l'autre : |a_2 = \dfrac{-1}{a_1}.|
Quelle est l'équation de la droite qui est perpendiculaire à celle identifiée dans le plan cartésien ci-dessous et qui passe par le point C?
| CALCULS | EXPLICATIONS |
|---|---|
|
|a_1 = \dfrac{\Delta y}{\Delta x} = \dfrac{0{,}7 - 2{,}5}{1{,}5 - 0} = -1{,}2| |
Trouver la pente de |\overline{AB}.| |
|
|\begin{align} a_1 \times a_2 &= -1 \\-1{,}2 \times a_2 &= -1 \\ a_2 &= \dfrac{-1}{-1{,}2} \\ a_2 &= 0{,}8\overline{3} \end{align}| |
Trouver la valeur de |a_2| de la droite passant par C en utilisant le fait que le produit des pentes de deux droites perpendiculaires vaut |-1.| |
|
|\begin{align} y &= a_2 x + b \\ y &= 0{,}8\overline{3}x + b \\ 2{,}25 &= 0{,}8\overline{3} (1{,}55) + b \\ 2{,}25 &\approx 1{,}29 + b \\ 0{,}96 &\approx b \end{align}| |
Trouver la règle de la droite passant par |C (1{,}55 ; 2{,}25)| sous la forme |y = a_2x + b.| |
|
Finalement, l'équation de la droite qui est perpendiculaire à |\overline{AB}| et qui passe par le point |C(1{,}55 ; 2{,}25)| est |y=0{,}8\overline{3}x + 0{,}96.| |
|
À voir aussi
| TYPES D'ÉVÉNEMENTS | DÉFINITION | EXEMPLE |
|---|---|---|
|
Mutuellement exclusifs |
Lorsqu'ils ne peuvent pas se produire en même temps. |
Lancer un dé à six faces et obtenir un résultat qui est à la fois un multiple de 3 et de 4. |
|
Non mutuellement exclusifs |
Lorsqu'ils peuvent se produire en même temps. |
Piger une carte au hasard dans un jeu qui en contient 52 et en obtenir une qui est à la fois un as et de couleur rouge. |
|
Dépendants |
Lorsque la réalisation de l'un affecte la réalisation de l'autre. |
Piger successivement et sans remise deux cartes dans un paquet qui en contient 52 au départ. |
|
Indépendants |
Lorsque la réalisation de l'un n'influe pas sur la réalisation de l'autre. |
Piger une carte dans un paquet qui en contient 52 et lancer un dé à six faces. |
Il ne faut pas oublier les types d'événements qui ont été vus dans les années précédentes (certaines, probables, impossibles, élémentaires, complémentaires, compatibles et incompatibles).
À voir aussi
Soit |a,| les chances pour et |b,| les chances contre, alors :
Rapport des chances pour |= a : b \Rightarrow \dfrac {a}{a+b}|
Rapport des chances contre |= b : a \Rightarrow \dfrac {b}{b+a}|
Ainsi, on obtient le gain net selon la proportion suivante : ||\dfrac{\text{Montant de la mise}}{\text{Gain net}} = \dfrac{\text{Nbre de chances sur lesquelles on mise}}{\text{Nbre total de chances}}||
À l'époque de l'hippodrome de Québec, on pouvait parier sur les victoires des chevaux de course. Ainsi, chaque cheval possédait une cote qui quantifiait ses chances de gagner. Pour la dernière course, un amateur a parié |20\ $| pour la victoire dont la cote était |1:14.| Ainsi, quel était le gain potentiel de son pari?
| CALCULS | EXPLICATIONS |
|---|---|
|
|\begin{align} \dfrac{20}{\text{Gain net}} &= \dfrac{\color{blue}{1}}{\color{blue}{1}+\color{red}{14}} \\\\ \dfrac{20}{\text{Gain net}} &= \dfrac{\color{blue}{1}}{15} \end{align}| |
Appliquer la proportion. |
|
|\begin{align} \dfrac{20}{\text{Gain net}} &= \dfrac{\color{blue}{1}}{15} \\\\ \text{Gain net} &= \dfrac{20 \times 15}{\color{blue}{1}} \\ \text{Gain net} &= 300 \end{align}| |
Résoudre avec le produit croisé. |
|
Si son cheval terminait en première place de la course, cet amateur repartirait avec la somme de |300\ $.| |
|
Pour certains combats de boxe, on peut parier sur la défaite d'un boxeur. Ainsi, chaque pugiliste possède une cote qui quantifie ses chances de gagner. Pour le prochain combat, le champion a une cote de |44:1| pour sa victoire. Ainsi, quel serait le gain net d'un amateur qui parierait |10\ $| contre une victoire du champion?
| CALCULS | EXPLICATIONS |
|---|---|
|
|\begin{align} \text{Rapport de chances pour} &= \color{blue}{44} : \color{red}{1} \\\\ \Rightarrow \text{Rapport de chances contre} &= \color{red}{1} : \color{blue}{44} \end{align}| |
Identifier le rapport des chances contre. |
|
|\begin{align} \dfrac{10}{\text{Gain net}} &= \dfrac{\color{red}{1}}{\color{red}{1}+\color{blue}{44}} \\\\ \dfrac{10}{\text{Gain net}} &= \dfrac{\color{red}{1}}{45} \end{align}| |
Appliquer la proportion. |
|
|\begin{align} \dfrac{10}{\text{Gain net}} &= \dfrac{\color{red}{1}}{45} \\\\ \text{Gain net} &= \dfrac{10 \times 45}{\color{red}{1}} \\ \text{Gain net} &= 450 \end{align}| |
Résoudre avec le produit croisé. |
|
Si le champion n'arrive pas à conserver sa ceinture, l'amateur de boxe gagnera |450\ $.| |
|
À voir aussi
|\mathbb{E} = (p_1 x_1 + p_2 x_2 + \dots + p_i x_i) - M|
où
|p_i =| Probabilité de réalisation de l'événement |i|
|x_i =| Montant associé à l'événement |i|
|M =| Montant de la mise initiale
Si |\mathbb{E} = 0|, alors le jeu est équitable.
Si |\mathbb{E} < 0|, alors le jeu est défavorable au joueur.
Si |\mathbb{E} >0|, alors le jeu est favorable au joueur.
Dans le but de financer l'équipe de ski acrobatique de l'école, des organisateurs mettent sur un pied une activité de financement pour laquelle il est possible de gagner les prix de participations suivants :
-
Un forfait de ski familial d'une fin de semaine (valeur de 800 $)
-
Deux billets de saison de ski alpin (valeur de 500 $ chacun)
-
Quatre paires de ski (valeur de 300 $ chacune)
-
Huit billets de remontée valide pour une journée (valeur de 45 $ chacun)
En sachant qu'ils ont un total de 336 billets à vendre, quel devrait être le prix de vente d'un billet de participation au tirage?
| CALCULS | EXPLICATIONS |
|---|---|
|
|\begin{align} \mathbb{E} &= (\color{blue}{p_1 x_1} + \color{red}{p_2 x_2} + \color{green}{p_3 x_3} + \color{black}{p_4 x_4}) - M \\\\ \mathbb{E} &= \left(\color{blue}{\dfrac{1}{336}\times 800 } + \color{red}{\dfrac{2}{336} \times 500} + \color{green}{\dfrac{4}{336} \times 300} + \color{black}{\dfrac{8}{336} \times 45}\right) - M \end{align}| |
Appliquer la formule de l'espérance mathématique. |
|
|\begin{align} \mathbb{E} &= \left(\color{blue}{\dfrac{1}{336}\times 800 } + \color{red}{\dfrac{2}{336} \times 500} + \color{green}{\dfrac{4}{336} \times 300} + \color{black}{\dfrac{8}{336} \times 45}\right) - M \\\\ 0 &= \left(\color{blue}{\dfrac{1}{336}\times 800 } + \color{red}{\dfrac{2}{336} \times 500} + \color{green}{\dfrac{4}{336} \times 300} + \color{black}{\dfrac{8}{336} \times 45}\right) - M \end{align}| |
Remplacer la valeur de |\mathbb{E}| par 0 puisque le jeu est équitable. |
|
|\begin{align} 0 &= \left(\color{blue}{\dfrac{1}{336}\times 800 } + \color{red}{\dfrac{2}{336} \times 500} + \color{green}{\dfrac{4}{336} \times 300} + \color{black}{\dfrac{8}{336} \times 45}\right) - M \\ 0 &= \left(\color{blue}{\dfrac{800}{336}} + \color{red}{\dfrac{1000}{336}} + \color{green}{\dfrac{1200}{336}} + \color{black}{\dfrac{360}{336}}\right) - M \\ 0 &= \dfrac{3360}{336} - M \\ M &= \dfrac{3360}{336} \\ M &= 10\ $ \end{align}| |
Isoler |M| pour trouver la valeur de la mise initiale. |
|
Pour que le jeu soit équitable, les billets doivent être vendus à un prix de |10\ $.| |
|
À voir aussi
|P(A \mid B) = \dfrac{P (A \cap B)}{P (B)}|
où |P(A) >0|
Au cours du mois précédent, les auditeurs d'une chaine de radio québécoise avaient la chance de gagner un voyage dans le domaine féérique de Walt Disney. Avant de faire le tirage au hasard du gagnant, le radiodiffuseur a dressé le portrait global des participants :
Ainsi, quelle est la probabilité que le gagnant soit père d'une famille de trois enfants en sachant qu'il s'est fait donner le billet de tirage en cadeau?
| CALCULS | EXPLICATIONS |
|---|---|
|
|P(\color{red}{B}) = \dfrac{\color{red}{15 + 30 + 2}}{23 + 12 + \dots + 67 + 27 } = \dfrac{\color{red}{47}}{240}| |
Identifier les cases qui font référence à ceux qui l'ont reçu en cadeau. |
|
|P(\color{blue}{A \cap B}) = \dfrac{\color{blue}{30}}{240}| |
Parmi les gens identifiés plus haut, identifier ceux qui ont une famille de trois enfants. |
|
|\begin{align} P(\color{blue}{A} \mid \color{red}{B}) &= \dfrac {P( \color{blue}{A \cap B})}{P(\color{red}{B})} \\ P(\color{blue}{A} \mid \color{red}{B}) &= \dfrac{\frac{\color{blue}{30}}{240}}{\frac{\color{red}{47}}{240}} \\ P(\color{blue}{A} \mid \color{red}{B}) &= \dfrac{\color{blue}{30}}{\color{red}{47}} \end{align}| |
Appliquer la formule. |
|
Ainsi, la probabilité que le gagnant soit un père d'une famille de trois enfants sachant qu'il s'est fait donner le billet en cadeau est de |\dfrac{30}{47}.| |
|
À voir aussi
|EM = \dfrac{\sum \mid x_i - \overline {x} \mid}{n}|
où
|x_i| représente chacune des données
|\sum| représente la somme
|n| représente le nombre total de données
Lors du dernier mois, 11 maisons ont été vendues dans un même quartier pour les montants suivants :
|\color{blue}{156\ 700\ $},| |\color{red}{158\ 900\ $},| |159\ 000\ $,| |162\ 500\ $,| |164\ 100\ $,| |167\ 400\ $,| |172\ 000\ $,| |175\ 000\ $,| |178\ 100\ $,| |179\ 000\ $,| |183\ 000\ $.|
À des fins de statistiques pour les agents immobiliers, calcule l'écart moyen de cette distribution.
| CALCULS | EXPLICATIONS |
|---|---|
|
|\dfrac{156\ 700 + 158\ 900 + \dots + 179\ 000 + 183\ 000}{11} = \color{green}{168\ 700}\ $| |
Calculer la moyenne selon |\dfrac {\sum x_i}{n}.| |
|
|\begin{align} \mid \color{blue}{156\ 700} - \color{green}{168\ 700}{\mid} &= 12\ 000 \\ \mid \color{red}{158\ 900} - \color{green}{168\ 700}{\mid} &= 9\ 800 \\ \mid 159\ 000 - \color{green}{168\ 700}{\mid} &= 9\ 700 \\ \mid 162\ 500 - \color{green}{168\ 700}{\mid} &= 6\ 200 \\ \mid 164\ 100 - \color{green}{168\ 700}{\mid} &= 4\ 600 \\ \mid 167\ 400 - \color{green}{168\ 700}{\mid} &= 1\ 300 \\ \mid 172\ 000 - \color{green}{168\ 700}{\mid} &= 3\ 300 \\ \mid 175\ 000 - \color{green}{168\ 700}{\mid} &= 6\ 300 \\ \mid 178\ 100 - \color{green}{168\ 700}{\mid} &= 9\ 400 \\ \mid 179\ 000 - \color{green}{168\ 700}{\mid} &= 10\ 300 \\ \mid 183\ 000 - \color{green}{168\ 700}{\mid} &= 14\ 300 \end{align}| |
Calculer les écarts à la moyenne de chacune des données. |
|
|EM = \dfrac{12\ 000+9\ 800+ \dots + 10\ 300 + 14\ 300}{11} \approx 7\ 927{,}27\ $| |
Calculer la moyenne des écarts à la moyenne. |
À voir aussi
Pour un échantillon : |s= \sqrt{\dfrac{\sum(x_{i}-\overline{x})^{2}}{n-1}}|
Pour une population : |\sigma = \sqrt{\dfrac{\sum(x_i-\mu)^2}{N}}|
où
|\sum| signifie qu’il faut effectuer une somme successive de plusieurs éléments.
|x_i| représente la |i^\text{e}| valeur de la distribution.
|\overline{x}| représente la moyenne de l’échantillon et |\mu,| la moyenne de la population.
|n| représente la taille de l’échantillon et |N,| la taille de la population.
Dans certains cours données à l'université, les professeurs attribuent les cotes en fonction des notes obtenues aux examens et à l'écart type de la distribution. Ainsi, quel est l'écart type de la distribution suivante :
| CALCULS | EXPLICATIONS |
|---|---|
|
|\begin{align} \mu &= \frac{78 + 52 + 45 + \dots + 45 + 60}{27} \\ \mu &\approx 63{,}11 \end{align}| |
Déterminer la moyenne |(\mu)| des résultats selon la population que représente la classe. |
|
|\begin{align} (78 - 63{,}11)^2 &\approx 221{,}71 \\ (52 - 63{,}11)^2 &\approx 123{,}43 \\ &\vdots \\ (45 - 63{,}11)^2 &\approx 327{,}97 \\ (60 - 63{,}11)^2 &\approx 9{,}67 \end{align}| |
Calculer le carré de la différence à la moyenne de chacune des données. |
|
|\sqrt{\dfrac{221{,}71 + 123{,}43 + \dots + 327{,}97 + 9{,}67}{27}} \approx 17{,}61 | |
Calculer la racine carrée de la moyenne des résultats précédents. |
|
Ainsi, l'écart type des notes des élèves de cette classe est d'environ |17{,}61.| |
|
À voir aussi
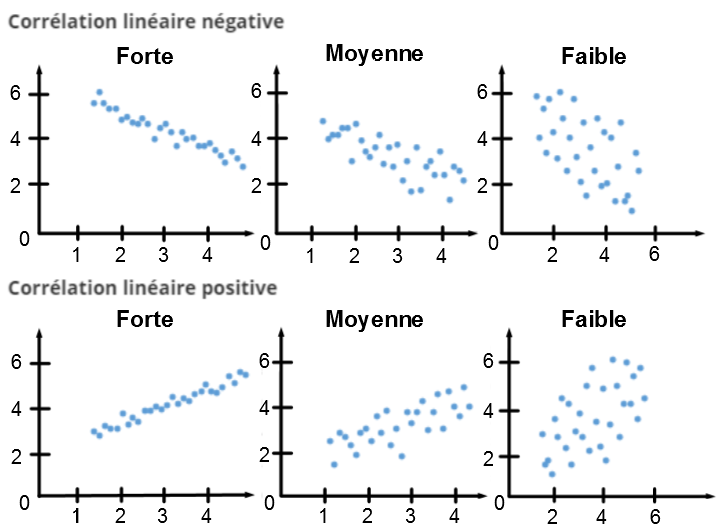
Le nuage de points est utilisé pour estimer la corrélation qui existe entre deux variables. Pour avoir une idée plus précise de la corrélation, il faut calculer le coefficient de corrélation.
Depuis cinq ans, une nouvelle entreprise ne cesse d'augmenter ses profits et cherche à agrandir son centre de production. Par contre, elle veut s'assurer que la croissance économique de sa compagnie soit positive et fortement régulière. Pour analyser le tout, voici le recensement des revenus commerciaux des 30 dernières semaines.
À ton avis, est-ce que la croissance économique de l'entreprise est positive et fortement régulière?
-
Tracer le nuage de points
-
Comparer le nuage de points à ceux qui servent de référence
Réponse : Selon le nuage de points tracé, on peut conclure que les revenus sont positifs et moyennement réguliers. Puisqu'ils ne sont pas fortement réguliers, il serait préférable d'attendre avant d'agrandir.
À voir aussi
Après avoir encadré le nuage de points et pris la mesure de la longueur |(L)| et la largeur |(l)| du rectangle :||r = \pm \left(1 - \dfrac{l}{L}\right)||Pour ce qui est du signe, il sera donné en fonction du sens du nuage de points.
On peut également utiliser ce coefficient pour qualifier la corrélation :
| Valeur de |r| | Force du lien linéaire |
|---|---|
| Près de |0| | Nulle |
| Près de |\pm 0{,}50| | Faible |
| Près de |\pm 0{,}75| | Moyenne |
| Près de |\pm 0{,}87| | Forte |
| Près de |\pm 1| | Très forte |
| |\pm 1| | Parfaite |
Afin de faire un bilan sur la réussite des étudiants qui s'inscrivent dans les établissements d'enseignements pour adultes, les membres de la direction s'intéressent à la corrélation entre l'absentéisme aux différents cours (en heures) et la moyenne générale (en %) à la fin de l'année scolaire. Pour bien analyser le tout, ils ont regroupé les données dans un nuage de points :
Quel est le coefficient de corrélation de cette étude?
| CALCULS | EXPLICATIONS |
|---|---|
| |
Tracer un rectangle, le plus petit possible, afin d'encadrer le nuage de points. |
| |
À l'aide d'une règle, mesurer la longueur |(L)| et la largeur |(l)| du rectangle. Dans ce cas, |\color{blue}{L = 13{,}5 \ \text{cm}}| |\color{red}{l = 2{,}8 \ \text{cm}}| |
|
|\begin{align} r &\approx \pm \left(1 - \dfrac{\color{red}{2{,}8}}{\color{blue}{13{,}5}}\right) \\ r &\approx \pm 0{,}79 \end{align}| |
Remplacer |L| et |l| dans la formule |r \approx \pm \left(1 - \dfrac{\color{red}{l}}{\color{blue}{L}}\right).| |
|
|r \approx - 0{,}79| |
Puisque le rectangle est orienté vers le bas (décroissant), le coefficient de corrélation est négatif. |
|
Le coefficient de corrélation entre le nombre d'heures d'absence et le résultat final en pourcentage est d'environ |-0{,}79,| ce qui signifie une corrélation négative moyenne. |
|
À voir aussi
Pour trouver l'équation de la droite de régression selon la méthode médiane-médiane, on peut se fier aux étapes suivantes :
-
Mettre les couples en ordre croissant selon la valeur des |x.|
-
Séparer les couples en trois groupes égaux, si possible.
-
Calculer la coordonnée médiane |(M_1, M_2, M_3)| de chacun des groupes.
-
Calculer la coordonnée moyenne |(P_1)| des trois points médians.
-
Calculer la valeur de la pente |(a)| avec |M_1| et |M_3.|
-
Calculer la valeur de la valeur initiale |(b)| avec |P_1.|
-
Écrire l'équation de la droite de régression sous la forme |y = ax + b.|
Avant de construire une nouvelle tour à condo et d'en faire l'emménagement paysager, on s'intéresse à la hauteur des arbres afin qu'ils ne cachent pas la vue aux futurs résidents pour au moins les 20 prochaines années. Pour estimer la hauteur de ces derniers, on utilise la table de valeurs suivante :
À l'aide de ces informations, détermine à quelle hauteur devrait se situer les premiers balcons afin que la vue ne soit pas obstruée par les arbres.
| CALCULS | EXPLICATIONS |
|---|---|
| |
Placer les couples en ordre croissant selon la valeur de la variable indépendante |(x)| en prenant soin de ne pas « défaire » les couples initiaux. |
| |
Séparer les couples en trois groupes égaux. Si ce n'est pas possible, on s'assure que le premier et le dernier groupe aient le même nombre de données. |
|
|M_1 = (1 , 29)| |M_2 = \left(\dfrac{2+3}{2}, \dfrac{54+58}{2}\right) = (2{,}5 ; 56)| |M_3 = (4 , 90)| |
Calculer la coordonnée médiane de chaque groupe. |
|
|\begin{align} \color{green}{P} &= \left(\frac{1 + 2{,}5 + 4}{3} , \frac{29 + 56 + 90}{3}\right) \\ &= \color{green}{(2{,}5 ; 58{,}33)} \end{align}| |
Calculer le point moyen en faisant la moyenne des |x| et des |y| des trois points médians. |
|
|\color{blue}{a} = \dfrac{\Delta y}{\Delta x} = \dfrac{90 - 29}{4 - 1} \approx 20{,}33| |
Selon l'équation de la droite de régression |y = \color{blue}{a}x + \color{red}{b}|, déterminer la valeur de |\color{blue}{a}| selon les points |M_1| et |M_3.| |
|
|\begin{align} y &= \color{blue}{20{,}33} x + \color{red}{b}\\ \color{green}{58{,}33} &= \color{blue}{20{,}33}(\color{green}{2{,}5}) + \color{red}{b} \\ \color{red}{7{,}503} &= \color{red}{b} \end{align}| Ainsi, |y = \color{blue}{20{,}33} x + \color{red}{7{,}503}| |
Trouver la valeur du paramètre |\color{red}{b}| en substituant |x| et |y| par les coordonnées du point |\color{green}{P}.| |
|
|\begin{align} y &= \color{blue}{20{,}33} x + \color{red}{7{,}503} \\ y &= \color{blue}{20{,}33} (20) + \color{red}{7{,}503} \\ y &= 414{,}103 \end{align}| |
Étant donné qu'on souhaite connaitre la hauteur des arbres après |20| ans, on substitue |x| par |20.| |
|
Après |20| ans, les arbres auront une hauteur d'environ |414{,}103\ \text{cm}.| Ainsi, les premiers balcons doivent être d'une hauteur minimale de |414{,}103\ \text{cm}.| |
|
Même si la situation et les données sont les mêmes, il est normal que la réponse finale varie selon la méthode utilisée (Méthode médiane-médiane ou Méthode de Mayer).
Puisque ce sont des méthodes qui servent à estimer et non à prédire les résultats avec certitude, il se peut qu'il y ait une différence entre les deux résultats.
À voir aussi
Pour trouver l'équation de la droite de régression selon la méthode de Mayer, on peut se fier aux étapes suivantes :
-
Mettre les couples en ordre croissant selon la valeur en |x.|
-
Séparer les couples en deux groupes égaux, si possible.
-
Calculer les points moyens |(P_1| et |P_2)| de chacun des groupes.
-
Utiliser ces points moyens pour trouver la valeur de la pente |(a)| et de la valeur initiale |(b).|
-
Écrire l'équation de la droite de régression sous la forme |y = ax + b.|
Avant de construire une nouvelle tour à condo et d'en faire l'emménagement paysager, on s'intéresse à la hauteur des arbres afin qu'ils ne cachent pas la vue aux futurs résidents pour au moins les 20 prochaines années. Pour estimer la hauteur de ces derniers, on utilise la table de valeurs suivante :
À l'aide de ces information, détermine à quelle hauteur devrait se situer les premiers balcons afin que la vue ne soit pas obstruée par les arbres.
| CALCULS | EXPLICATIONS |
|---|---|
| |
Il faut d'abord placer les couples en ordre croissant selon la valeur de la variable indépendante, sans défaire les couples initiaux. |
| |
Si possible, séparer la distribution en deux groupes égaux. |
|
|\begin{align} P_1 &= \left(\dfrac{\color{red}{1+1+... +2+2}}{7}, \dfrac{\color{blue}{21+23+...+42+54}}{7}\right) \\ &\approx (\color{red}{1{,}43} ; \color{blue}{34{,}29}) \\\\ P_2 &= \left(\dfrac{\color{green}{3+3...+4+4}}{7}, \dfrac{58+59+...+90+97}{7}\right) \\ &\approx (\color{green}{3{,}43} ; 76) \end{align}| |
Calculer les points moyens de chancun des groupes. |
|
|a = \dfrac{\Delta y}{\Delta x} = \dfrac{76 - \color{blue}{34{,}29}}{\color{green}{3{,}43} - \color{red}{1{,}43}} \approx 20{,}86| Ainsi, |y = 20{,}86x + b.| Par substitution des coordonnées de |P_1:| ||\begin{align} y &= 20{,}86x + b \\ 34{,}29 &= 20{,}86 (1{,}43) + b \\ 34{,}29 &= 29{,}83 + b \\ 4{,}46 &= b \end{align}|| Ainsi, |y = 20{,}86x + 4{,}46.| |
Trouver l'équation de la droite de régression sous la forme |y = ax + b| selon les points |P_1| et |P_2.| |
|
|\begin{align} y &= 20{,}86x + 4{,}46 \\ y &= 20{,}86 (20) +4{,}46 \\ y &= 417{,}2 + 4{,}46 \\ y &= 421{,}66 \end{align}| |
Étant donné qu'on souhait connaitre la hauteur des arbres après |20| ans, on substitue |x| par |20.| |
|
Après |20| ans, les arbres auront une hauteur d'environ |421{,}66\ \text{cm}.| Ainsi, les premiers balcons doivent être d'une hauteur minimale de |421{,}66\ \text{cm}.| |
|
Même si la situation et les données sont les mêmes, il est normal que la réponse finale varie selon la méthode utilisée (Méthode médiane-médiane ou Méthode de Mayer).
Puisque ce sont des méthodes qui servent à estimer et non à prédire les résultats avec certitude, il se peut qu'il y ait une différence entre les deux résultats.