This Crash Course focuses on problem-solving in relation to the functions studied in Secondary 4 and 5.
The problems covered in this Crash Course relate to the following functions: the quadratic function, the greatest integer function, the square root function, the absolute value function, the rational function, the exponential function and the logarithmic function.
You need to be able to graph and find the rule for all these functions. You must also be able to solve all these types of equations.
Basic Quadratic Function
||f(x)=ax^2||
Transformed Quadratic Function
||f(x)=a(x-h)^2+k||where |(h,k)| are the coordinates of the vertex
Here are two examples of solving a quadratic equation in standard form:
Consider the function: |f(x)=3(x+7)^2-5|
-
Determine the value(s) of |x| when |f(x)=7.| ||\begin{aligned}f(x)&=3(x+7)^2-5\\7&=3(x+7)^2-5\\\color{#ec0000}{\sqrt{\color{black}{4}}}&=\color{#ec0000}{\sqrt{\color{black}{(x+7)^2}}}\\\pm2&=x+7\end{aligned}\\ \begin{aligned}\\-2&=x+7&2&=x+7\\-9&=x_1&-5&=x_2\end{aligned}||
-
Determine the value(s) of |x| when |f(x)=-8.| ||\begin{align}f(x)&=3(x+7)^2-5\\ -8&=3(x+7)^2-5\\-1&=(x+7)^2\quad \Rightarrow \text{impossible}\end{align}||The square of a number is always positive, but the number on the left of the equation is not a positive number. Therefore, you can stop solving since there is no solution when |f(x)=-8.|
If the equation was given in general form, set everything equal to zero: |ax^2+bx+c=0| and use the quadratic formula.
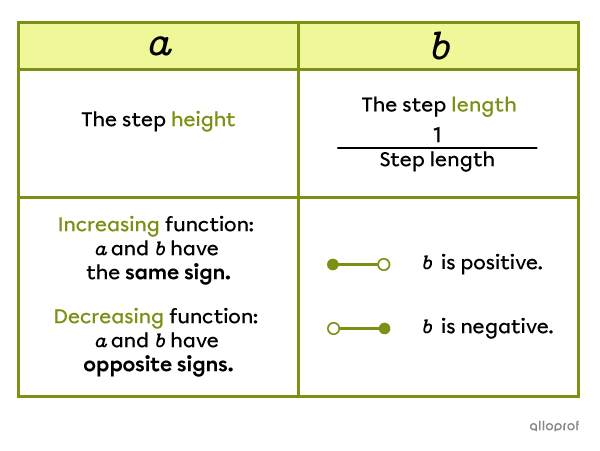
Basic Step Function
||f(x) = a[bx]||
Transformed Step Function
||f(x) = a[b(x-h)]+k||where |(h,k)| corresponds to the coordinates of a closed point
Here are two examples of solving greatest integer equations:
Consider the function: |f(x)=-2[8(x-3)]+1|
-
Determine the value of |x| when |f(x)=2.| ||\begin{align}f(x)&=-2[8(x-3)]+1\\ 2&=-2[8(x-3)]+1\\-\dfrac{1}{2}&=[8(x-3)]\quad \Rightarrow \text{impossible}\end{align}||Since the greatest integer is not a whole number, stop solving. There is no solution when |f(x)=2.|
-
Determine the value of |x| when |f(x)=-5.| ||\begin{gathered}\begin{aligned}f(x)&=-2[8(x-3)]+1\\-5&=-2[8(x-3)]+1\\3&=[8(x-3)]\end{aligned}\\\\\begin{alignat}{13}3&\leq8(x-3)&&<3+1\\\dfrac{3}{8}&\leq\ \ \,x-3&&<\dfrac{4}{8}\\\dfrac{3}{8}+3&\leq\quad\ x&&<\dfrac{1}{2}+3\\\dfrac{27}{8}&\leq\quad\ x&&<\dfrac{7}{2}\end{alignat}\\\\x\in\left[\dfrac{27}{8},\dfrac{7}{2}\right[\end{gathered}||
Basic Square Root Function
||f(x)=a\sqrt{bx}||
Transformed Square Root Function
||f(x)=a\sqrt{b(x-h)}+k||where |(h,k)| are the coordinates of the vertex
Two key restrictions must be taken into consideration:
-
A square root is always greater than or equal to |0.|
-
The term under the square root, called the radicand, is always greater than or equal to |0.|
Here are 2 examples of solving a square root equation:
Consider the function: |f(x)=-7\sqrt{-(x+1)}+4.|
-
Determine the value(s) of |x| when |f(x)=-2.| ||\begin{align}f(x)&=-7\sqrt{-(x+1)}+4\\-2&=-7\sqrt{-(x+1)}+4\\\left(\dfrac{6}{7}\right)^{\boldsymbol{\color{#ec0000}{2}}}&=\sqrt{-(x+1)}^{\boldsymbol{\color{#ec0000}{2}}}\\\dfrac{36}{49}&=-(x+1)\\-\dfrac{36}{49}&=x+1\\-\dfrac{85}{49}&=x\end{align}||
-
Determine the value(s) of |x| when |f(x)=6.| ||\begin{align}f(x)&=-7\sqrt{-(x+1)}+4\\6&=-7\sqrt{-(x+1)}+4\\-\dfrac{2}{7}&=\sqrt{-(x+1)}\quad\Rightarrow\text{impossible}\end{align}||Since the square root of a number cannot be negative, stop solving. There is no solution when |f(x)=6.|
Transformed Absolute Value Function
||f(x)=a\vert x-h\vert+k||where |(h,k)| corresponds to the coordinates of the vertex
When an absolute value is isolated to one side of the equation, the algebraic expression or the number on the other side must be positive.||\vert x\vert=\underbrace{\dots}_{\ge\ 0}||
Here are two examples of solving an absolute value equation:
Consider the function: |f(x)=-0.6\vert x-3\vert -1|
-
Determine the value(s) of |x| when |f(x)=-10.| ||\begin{aligned}f(x)&=-0.6\vert x-3\vert -1\\-10&=-0.6\vert x-3\vert -1\\15&=\vert x-3\vert\end{aligned}\\\begin{aligned}\\15&=x-3&-15&=x-3\\18&=x_1&-12&=x_2\end{aligned}||The corresponding |x| values are |-12| and |18.|
-
Determine the value(s) of |x| when |f(x)=5.| ||\begin{align}f(x)&=-0.6\vert x-3\vert-1\\5&=-0.6\vert x-3\vert-1\\6&=-0.6\vert x-3\vert\\-10&=\vert x-3\vert\quad\Rightarrow\quad\text{impossible}\end{align}||Since the absolute value is equal to a negative number, stop solving. There is no solution when |f(x)=5.|
There are 2 ways of writing the rule of a rational function.
Standard form
||f(x)=\dfrac{a}{b(x-h)}+k||where
|x=h| is the equation of the vertical asymptote.
|y=k| is the equation of the horizontal asymptote.
Note: In most cases, the simplified standard form is used: ||f(x)=\dfrac{a}{x-h}+k||
General form
||f(x)=\dfrac{a_1x+b_1}{a_2x+b_2}||
In some problems, it is necessary to switch from one form to another.
To switch from standard to general form, write both terms over the same denominator and add the numerators.
Example: ||\begin{align}f(x)&=\dfrac{5}{x-3}+4\\&=\dfrac{5}{x-3}+\dfrac{4\boldsymbol{\color{#ec0000}{(x-3)}}}{1\boldsymbol{\color{#ec0000}{(x-3)}}}\\&=\dfrac{5}{x-3}+\dfrac{4x-12}{x-3}\\&=\dfrac{5+4x-12}{x-3}\\&=\dfrac{4x-7}{x-3}\end{align}||
To switch from general form to standard form, divide the numerator by the denominator.
Example: ||\begin{align}f(x)&=\dfrac{8x-15}{2x-6}\\\\&\quad\ \boldsymbol{\color{#333fb1}{4}}\\\boldsymbol{\color{#ff55c3}{2x-6}}\quad&\overline{\smash{\big)}\ \ \ 8x-15\ \,}\\&\underline{-\ (8x-24)}\\&\qquad\quad\ \boldsymbol{\color{#3a9a38}{9}}\phantom{)}\\\\f(x)&=\dfrac{\boldsymbol{\color{#3a9a38}{9}}}{\boldsymbol{\color{#ff55c3}{2x-6}}}+\boldsymbol{\color{#333fb1}{4}}\\&=\dfrac{9}{2(x-3)}+4\end{align}||
Here are two examples of solving a rational equation:
Consider the function: |f(x)=\dfrac{3}{x-4}+2.|
-
Determine the value of |x| when |f(x)=7.| ||\begin{align}f(x)&=\dfrac{3}{x-4}+2\\7&=\dfrac{3}{x-4}+2\\5&=\dfrac{3}{\boldsymbol{\color{#ec0000}{(x-4)}}}\\5\boldsymbol{\color{#ec0000}{(x-4)}}&=3\\5x-20&=3\\5x&=23\\x&=4.6\end{align}||
Consider the function: |f(x)=\dfrac{6x+21}{2x+8}.|
-
Determine the value of |x| when |f(x)=3.| ||\begin{align}f(x)&=\dfrac{6x+21}{2x+8}\\3&=\dfrac{6x+21}{\boldsymbol{\color{#ec0000}{2x+8}}}\\3\boldsymbol{\color{#ec0000}{(2x+8)}}&=6x+21\\6x+24&=6x+21\\24&\boldsymbol{\color{#ec0000}{=}}21\qquad\Rightarrow\text{False!}\end{align}||Since the result is a false equality, it means that there is no solution. |3| is the value of one of the asymptotes.
Basic Exponential Function
||f(x)=a(c)^{bx}||where
|y=0| corresponds to the equation of the horizontal asymptote.
|a| corresponds to the initial value.
Transformed Exponential Function
||f(x)=a(c)^{b(x-h)}+k||where
|y=k| corresponds to the equation of the horizontal asymptote.
|a+k| corresponds to the initial value.
Note: Most of the time, the simplified standard form is used. ||f(x)=a(c)^x +k||
-
Parameter |c| corresponds to the multiplicative factor.
-
Parameter |b| represents the number of times the multiplicative factor is applied within a given period of time.
To switch from exponential form to logarithmic form, the following diagram can be used:

Example: ||\boldsymbol{\color{#EC0000}{46}}=\boldsymbol{\color{#51B6C2}3^{\color{#3A9A38}{2x}}}\quad\Leftrightarrow\quad\boldsymbol{\color{#3A9A38}{2x}}=\log_\boldsymbol{\color{#51B6C2}3}\boldsymbol{\color{#EC0000}{46}}||
Here are two examples of solving exponential equations:
Consider the function: |f(x)=\dfrac{1}{8}(4)^x+5|
-
Determine the value(s) of |x| when |f(x)=13.| ||\begin{gather}\begin{aligned}f(x)&=\dfrac{1}{8}(4)^x+5\\13&=\dfrac{1}{8}(4)^x+5\\8&=\dfrac{1}{8}(4)^x\\\boldsymbol{\color{#EC0000}{64}}&=\boldsymbol{\color{#51B6C2}4^\color{#3A9A38}x}\end{aligned}\\\Updownarrow\\\begin{aligned}\boldsymbol{\color{#3A9A38}x}&=\log_{\boldsymbol{\color{#51B6C2}4}}\boldsymbol{\color{#EC0000}{64}}\\x&=3\end{aligned}\end{gather}||
-
Determine the value(s) of |x| when |f(x)=2.| ||\begin{gather}\begin{aligned}f(x)&=\dfrac{1}{8}(4)^x+5\\2&=\dfrac{1}{8}(4)^x+5\\-3&=\dfrac{1}{8}(4)^x\\\boldsymbol{\color{#EC0000}{-24}}&=\boldsymbol{\color{#51B6C2}4^\color{#3A9A38}x}\end{aligned}\\\Updownarrow\\\begin{aligned}\boldsymbol{\color{#3A9A38}x}&=\log_{\boldsymbol{\color{#51B6C2}4}}(\boldsymbol{\color{#EC0000}{-24}})\end{aligned}\end{gather}||Since the argument of a logarithm can never be less than |0,| there is no solution.
Basic Logarithmic Function
||f(x)=a\log_c({bx})||where
|x=0| corresponds to the equation of the vertical asymptote.
Transformed Logarithmic Function
||f(x)=a\log_c\big({b(x-h})\big)+k||where
|x=h| corresponds to the equation of the horizontal asymptote.
Note: Most of the time, the simplified standard form is used. ||f(x)=\log_c\big({b(x-h})\big)||
To switch from logarithmic form to exponential form, the following diagram can be used:
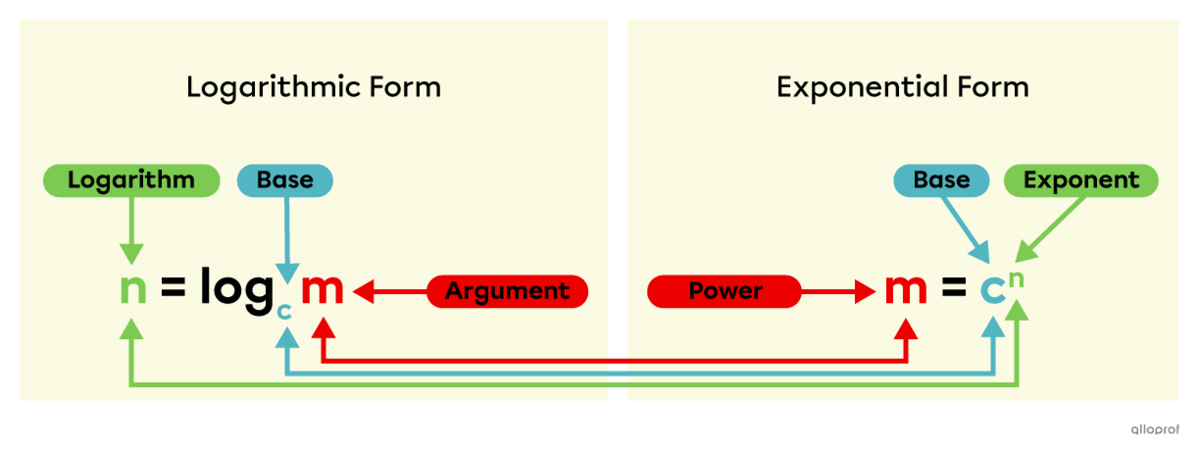
Example: ||\boldsymbol{\color{#3A9A38}{10}}=\log_\boldsymbol{\color{#51B6C2}2}\boldsymbol{\color{#EC0000}x}\quad\Leftrightarrow\quad\boldsymbol{\color{#EC0000}x}=\boldsymbol{\color{#51B6C2}2^{\color{#3A9A38}{10}}}||The natural logarithm is a logarithm with a base value of |e.| The number |e| is an irrational number whose value is approximately |2.718\ 28...| ||\ln x=\log_e x||where ||e\approx 2.72||
Here is an example of solving logarithmic equations:
Consider the function: |f(x)=-\log_{\frac{3}{2}}\left(\dfrac{1}{6}(x+3)\right)-2|
-
Determine the value(s) of |x| when |f(x)=-3.| ||\begin{gather}\begin{aligned}f(x)&=-\log_{\frac{3}{2}}\left(\dfrac{1}{6}(x+3)\right)-2\\-3&=-\log_{\frac{3}{2}}\left(\dfrac{1}{6}(x+3)\right)-2\\-1&=-\log_{\frac{3}{2}}\left(\dfrac{1}{6}(x+3)\right)\\\boldsymbol{\color{#3A9A38}1}&=\log_{\boldsymbol{\color{#51B6C2}{\frac{3}{2}}}}\left(\boldsymbol{\color{#EC0000}{\dfrac{1}{6}(x+3)}}\right)\end{aligned}\\\Updownarrow\\\begin{aligned}\boldsymbol{\color{#EC0000}{\dfrac{1}{6}(x+3)}}&=\left(\boldsymbol{\color{#51B6C2}{\frac{3}{2}}}\right)^{\boldsymbol{\color{#3A9A38}1}}\\x+3&=9\\x&=6\end{aligned}\end{gather}||